Other
Survey/expository papers
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 1
-
- Article
- Export citation
Research Article
Alfred Tarski's work in set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 2-6
-
- Article
- Export citation
Alfred Tarski's elimination theory for real closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 7-19
-
- Article
- Export citation
Alfred Tarski and decidable theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 20-35
-
- Article
- Export citation
Alfred Tarski's work on general metamathematics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 36-50
-
- Article
- Export citation
Tarski on truth and logical consequence
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 51-79
-
- Article
- Export citation
Philosophical implications of Tarski's work1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 80-91
-
- Article
- Export citation
Seminormal λ-generated ideals on P κ λ
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 92-102
-
- Article
- Export citation
Correction to “Simple r. e. degree structures”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 103-104
-
- Article
- Export citation
Equalization of finite flowers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 105-123
-
- Article
- Export citation
MM. Borel, Tits, Zil′ber et le Général Nonsense
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 124-131
-
- Article
- Export citation
Missionary mathematics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 132-145
-
- Article
- Export citation
Vaught's conjecture for o-minimal theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 146-159
-
- Article
- Export citation
Boolean simple groups and boolean simple rings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 160-173
-
- Article
- Export citation
A high strongly noncappable degree
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 174-187
-
- Article
- Export citation
Definability in reducts of algebraically closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 188-199
-
- Article
- Export citation
On a theory of weak implications
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 200-211
-
- Article
- Export citation
Σ2 -collection and the infinite injury priority method
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 212-221
-
- Article
- Export citation
Relational structures determined by their finite induced substructures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 222-230
-
- Article
- Export citation
A downward Löwenheim-Skolem theorem for infinitary theories which have the unsuperstability property
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 231-242
-
- Article
- Export citation



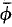 (
(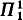 indescribable subsets of κ, then
indescribable subsets of κ, then 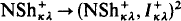 (where NSh
(where NSh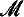 ⊨ “
⊨ “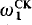 -nonstandard, then
-nonstandard, then 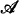 = s.p.(
= s.p.(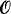 = deg{
= deg{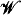 = deg{
= deg{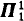 -determinacy (see a forthcoming paper by Girard and Kechris).
-determinacy (see a forthcoming paper by Girard and Kechris).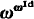 is the (smallest) equalizer for Fl
is the (smallest) equalizer for Fl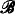 be a complete Boolean algebra and
be a complete Boolean algebra and 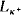 ,
,