Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-24T14:45:00.844Z Has data issue: false hasContentIssue false
  • English
  • Français

Alfred Tarski's elimination theory for real closed fields

Published online by Cambridge University Press:  12 March 2014

Lou Van Den Dries
Lou Van Den Dries*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, Illinois 61801
Get access Rights & Permissions [Opens in a new window]

Extract

Tarski made a fundamental contribution to our understanding of R, perhaps mathematics’ most basic structure. His theorem is the following.

To any formula ϕ(X1, …, Xm) in the vocabulary {0, 1, +, ·, <} one can effectively associate two objects: (i) a quantifier free formula 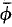(X 1, …, Xm ) in

(1) the same vocabulary, and (ii) a proof of the equivalence ϕ ↔ 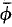that uses only the axioms for real closed fields. (Reminder: real closed fields are ordered fields with the intermediate value property for polynomials.)

Everything in (1) has turned out to be crucial: that arbitrary formulas are considered rather than just sentences, that the equivalence ϕ ↔ 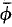holds in all real closed fields rather than only in R; even the effectiveness of the passage from ϕ to 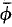has found good theoretical uses besides firing the imagination.

We begin this survey with some history in §1. In §2 we discuss three other influential proofs of Tarski's theorem, and in §3 we consider some of the remarkable and totally unforeseen ways in which Tarski's theorem functions nowadays in mathematics, logic and computer science.

I thank Ward Henson, and in particular Wilfrid Hodges without whose constant prodding and logistic support this article would not have been written.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 53 , Issue 1 , March 1988 , pp. 7 - 19
Copyright
Copyright © Association for Symbolic Logic 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Artin, E. [1927] Über die Zerlegung definiter Funktionen in Quadrate, Abhandlungen aus dem Mathematischen Seminar der Hansischen Unhersität, vol. 5, pp. 100–115.CrossRefGoogle Scholar
Artin, E. and Schreier, O. [1926] Algebraische Konstruktion reeller Körper, Abhandlungen aus dent Mathematischen Seminar der Hansischen Unhersität, vol. 5, pp. 83–99.Google Scholar
Ax, J. [1968] The elementary theory of finite fields, Annals of Mathematics, ser. 2, vol. 88, pp. 239–271.CrossRefGoogle Scholar
Ax, J. and Kochen, S. [1965a] Diophantine problems over local fields. I, American Journal of Mathematics, vol. 87, pp. 605–630.CrossRefGoogle Scholar
Ax, J. and Kochen, S. [1965b] Diophantine problems over local fields. II: A complete set of axioms for p-adic number theory, American Journal of Mathematics, vol. 87, pp. 631–648.CrossRefGoogle Scholar
Ax, J. and Kochen, S. [1966] Diophantine problems over local fields. III: Decidable fields , Annals of Mathematics, ser. 2, vol. 83, pp. 437–456.CrossRefGoogle Scholar
Becker, E. [1986] On the real spectrum of a ring and its application to semialgebraic geometry, Bulletin (New Series) of the American Mathematical Society, vol. 5, pp. 19–60.CrossRefGoogle Scholar
Blum, L. [1977] Differentially closed fields: a model-theoretic tour, Contributions to algebra (collection of papers dedicated to Ellis Kolchin), Academic Press, New York, pp. 37–61.Google Scholar
Brumfiel, G. W. [1979] Partially ordered rings and semi-algebraic geometry, London Mathematical Society Lecture Note Series, vol. 37, Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Chang, C. C. and Keisler, H. J. [1973] Model theory, North-Holland, Amsterdam.Google Scholar
Cherlin, G. and Dickmann, M. A. [1983] Real closed rings. II: Model theory, Annals of Pure and Applied Logic, vol. 25, pp. 213–231.CrossRefGoogle Scholar
Shang-Ching, Chou [1984] Proving elementary geometry theorems using Wu's algorithm, Automated theorem proving: After 25 years, Contemporary Mathematics, vol. 29, American Mathematical Society, Providence, Rhode Island, pp. 243–286.Google Scholar
Cohen, P. J. [1969] Decision procedures for real and p-adic fields, Communications in Pure and Applied Mathematics, vol. 22, pp. 131–151.CrossRefGoogle Scholar
Collins, G. E. [1975] Quantifier elimination for real closed fields by cylindrical algebraic decomposition, Automata theory and formal languages, second GI conference, Kaiserslautern, 1975, Lecture Notes in Computer Science, vol. 33, Springer-Verlag, Berlin, pp. 134–183.CrossRefGoogle Scholar
Collins, G. E. [1982] Quantifier elimination for real closed fields: a guide to the literature, Computer algebra. Symbolic and algebraic computation, Computing Supplementum, vol. 4, Springer-Verlag, Vienna, pp. 79–81.Google Scholar
Coste, M. [1982] Ensembles semi-algébriques, Géométric algébrique réelle et formes quadratiques (Rennes, 1981), Lecture Notes in Mathematics, vol. 959, Springer-Verlag, Berlin, pp. 109–138.CrossRefGoogle Scholar
Coste, M. and Coste-Roy, M. F. [1982] La topologie du spectre réel, Ordered fields and real algebraic geometry, Contemporary Mathematics, vol. 8, American Mathematical Society, Providence, Rhode Island, pp. 27–59.CrossRefGoogle Scholar
Dahn, B. [1984] The limit behaviour of exponential terms, Fundamenta Mathematicae, vol. 124, pp. 169–186.CrossRefGoogle Scholar
Delfs, H. and Knebusch, M. [1981] Semialgebraic topology over a real closed field. II: Basic theory of semialgebraic spaces, Mathematische Zeitschrift, vol. 178, pp. 175–213.CrossRefGoogle Scholar
Delzell, C. N. [1984] A continuous, constructive solution to Hubert's 17th problem, Inventiones Mathematicae, vol. 76, pp. 365–384.CrossRefGoogle Scholar
Denef, J. [1984] The rationality of the Poincaré series associated to the p-adic points on a variety, Inventiones Mathematicae, vol. 77, pp. 1–23.CrossRefGoogle Scholar
Denef, J. and Van Den Dries, L. [1988] Real and p-adic subanalytic sets, Annals of Mathematics (to appear).Google Scholar
Dickmann, M. A. [1985] Applications of model theory to real algebraic geometry. A survey, Methods in mathematical logic (proceedings of the sixth Latin American symposium on mathematical logic, Caracas, 1983), Lecture Notes in Mathematics, vol. 1130, Springer-Verlag, Berlin, pp. 76–150.Google Scholar
Van Den Dries, L. [1978] Model theory of fields, Thesis, University of Utrecht, Utrecht.Google Scholar
Van Den Dries, L. [1984] Algebraic theories with definable Skolem functions, this Journal, vol. 49, pp. 625–629.Google Scholar
Van Den Dries, L. [1986] A generalization of the Tarski-Seidenberg theorem, and some nondefinability results, Bulletin (New Series) of the American Mathematical Society, vol. 15, pp. 189–193.CrossRefGoogle Scholar
Eršov, Yu. L. [1965] On the elementary theory of maximal normed fields, Algebra i Logika, vol. 4, no. 3, pp. 31–70. (Russian)Google Scholar
Eršov, Yu. L. [1966] On the elementary theory of maximal normed fields. II, Algebra i Logika, vol. 5, no. 1, pp. 5–40. (Russian)Google Scholar
Eršov, Yu. L. [1967] On the elementary theory of maximal normed fields. III, Algebra i Logika, vol. 6, no. 3, pp. 31–38. (Russian)Google Scholar
Fried, M. and Jarden, M. [1986] Field arithmetic, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Gabrièlov, A. [1968] Projections of semi-analytic sets, Functional Analysis audits Applications, vol. 2, pp. 282–291.CrossRefGoogle Scholar
Gorin, E. A. [1961] Asymptotic properties of polynomials and algebraic functions of several variables, Russian Mathematical Surveys, vol. 16, no. 1, pp. 93–119.Google Scholar
Grothendieck, A. [1964] Éléments de Géométrie algébrique. IV: Étude locale des schémas et des morphismes de schémas. I, Institut des Hautes Études Scientifiques, Publications Mathématiques, vol. 20.Google Scholar
Grunewald, F. and Segal, D. [1980] Some general algorithms. I, II, Annals of Mathematics, ser. 2, vol. 112, pp. 531–583, 585–617.Google Scholar
Hardt, R. [1980] Semi-algebraic local triviality in semi-algebraic mappings, American Journal of Mathematics, vol. 102, pp. 291–302.CrossRefGoogle Scholar
Henkin, L. [1960] Sums of squares, Summaries of talks presented at the summer institute for symbolic logic, Cornell University, 1957, 2nd ed., Institute for Defense Analyses, Princeton, New Jersey, pp. 284–291.Google Scholar
Hilbert, D. [1899] Grundlagen der Geometrie, Teubner, Leipzig.Google Scholar
Hironaka, H. [1973a] Subanalytic sets, Number theory, algebraic geometry and commutative algebra, in honor of Y. Akizuki, Kinokuniya, Tokyo, pp. 453–493.Google Scholar
Hironaka, H. [1973b] Introduction to real-analytic sets and real-analytic maps, Lecture notes, Istituto Matematico “L. Tonelli”, Pisa.Google Scholar
Hörmander, L. [1955] On the theory of general partial differential operators, Acta Mathematica, vol. 94, pp. 161–248.CrossRefGoogle Scholar
Hörmander, L. [1983] The analysis of linear partial differential operators. II, Springer-Verlag, Berlin.Google Scholar
Hovanskiĭ, A. G. [1980] On a class of systems of transcendental equations, Soviet Mathematics Doklady, vol. 22, pp. 762–765.Google Scholar
Hovanskiĭ, A. G. [1985] Fewnomials and Pfaff manifolds, Proceedings of the international congress of mathematicians (Warsaw, 1983), vol. 1, PWN, Warsaw, and North-Holland, Amsterdam, pp. 549–564.Google Scholar
Kreisel, G. [1960] Sums of squares, Summaries of talks presented at the summer institute for symbolic logic, Cornell University, 1957, 2nd ed., Institute for Defense Analyses, Princeton, New Jersey, pp. 313–320.Google Scholar
Lam, T. Y. [1984] An introduction to real algebra, Rocky Mountain Journal of Mathematics, vol. 14, pp. 767–814.CrossRefGoogle Scholar
Łojasiewicz, S. [1964] Triangulations of semi-analytic sets, Annali delta Scuola Normale Superiore di Pisa, ser. 3, vol. 18, pp. 449–474.Google Scholar
Łojasiewicz, S. [1965] Ensembles semi-analytiques, Lecture notes, École Polytechnique, Paris.Google Scholar
Macintyre, A. [1976] On definable subsets of p-adic fields, this Journal, vol. 41, pp. 605–610.Google Scholar
Macintyre, A. [1986] Twenty years of p-adic model theory, Logic Colloquium '84, North-Holland, Amsterdam, pp. 121–153.CrossRefGoogle Scholar
Macintyre, A., McKenna, K. and van den Dries, L. [1983] Elimination of quantifiers in algebraic structures, Advances in Mathematics, vol. 47, pp. 74–87.Google Scholar
Poizat, B. [1983] Une théorie de Galois imaginaire, this Journal, vol. 48, pp. 1151–1170.Google Scholar
Prestel, A. and Roquette, P. [1984] Formally p-adic fields, Lecture Notes in Mathematics, vol. 1050, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Robinson, A. [1955] On ordered fields and definite functions, Mathematische Annalen, vol. 130, pp. 257–271.CrossRefGoogle Scholar
Robinson, A. [1956a] Complete theories, North-Holland, Amsterdam.Google Scholar
Robinson, A. [1956b] Further remarks on ordered fields and definite functions, Mathematische Annalen, vol. 130, pp. 405–409.CrossRefGoogle Scholar
Robinson, A. [1957] Some problems of definability in the lower predicate calculus, Fundamenta Mathematicae, vol. 44, pp. 309–329.CrossRefGoogle Scholar
Robinson, A. [1958] Relative model-completeness and the elimination of quantifiers, Dialectica, vol. 12, pp. 394–407.CrossRefGoogle Scholar
Robinson, A. [1959a] On the concept of a differentially closed field, Bulletin of the Research Council of Israel, Section F: Mathematics and Physics, vol. 8, pp. 113–128.Google Scholar
Robinson, A. [1959b] Solution of a problem of Tarski, Fundamenta Mathematicae, vol. 47, pp. 179–204.CrossRefGoogle Scholar
Robinson, A. and Zakon, E. [1960] Elementary properties of ordered Abelian groups, Transactions of the American Mathematical Society, vol. 96, pp. 222–236.CrossRefGoogle Scholar
Robinson, J. [1949] Definability and decision problems in arithmetic, this Journal, vol. 14, pp. 98–114.Google Scholar
Sacks, G. E. [1972] Saturated model theory, Benjamin, Reading, Massachusetts.Google Scholar
Seidenberg, A. [1954] A new decision method for elementary algebra, Annals of Mathematics, ser. 2, vol. 60, pp. 365–374.CrossRefGoogle Scholar
Seidenberg, A. [1956] An elimination theory for differential algebra, University of California Publications in Mathematics, New Series, vol. 3, pp. 31–66.Google Scholar
Shelah, S. [1973] Differentially closed fields, Israel Journal of Mathematics, vol. 16, pp. 314–328.CrossRefGoogle Scholar
Shoenfield, J. L. [1971] A theorem on quantifier elimination, Symposia Mathematica, vol. 5 (INDAM, Rome, 1969/1970), Academic Press, London, pp. 173–176.Google Scholar
Shoenfield, J. L. [1977] Quantifier elimination in fields, Non-classical logics, model theory and computability (proceedings of the third Latin American symposium on mathematical logic, Campinas, 1976), North-Holland, Amsterdam, pp. 243–252.Google Scholar
Thom, R. [1962] La stabilité topologique des applications polynomials, L’Enseignement Mathématique, ser. 2, vol. 8, pp. 24–33.Google Scholar
Vaught, R. L. [1986] Tarski's work in model theory, this Journal, vol. 51, pp. 869–882.Google Scholar
van der Waerden, B. L. [1937] Moderne Algebra. Vol. I, 2nd ed., Springer-Verlag, Berlin.CrossRefGoogle Scholar
Wang, Hao [1984] Computer theorem proving and artificial intelligence, Automated theorem proving: after 25 years, Contemporary Mathematics, vol. 29, American Mathematical Society, Providence, Rhode Island, pp. 49–70.CrossRefGoogle Scholar
Wen-Tsün, Wu [1984] On the decision problem and the mechanization of theorem proving in elementary geometry, Automated theorem proving: after 25 years, Contemporary Mathematics, vol. 29, American Mathematical Society, Providence, Rhode Island, pp. 213–234.Google Scholar
Ziegler, M. [1982] Einige unentscheidbare Körpertheorien, L’Enseignement Mathématique, ser. 2, vol. 28, pp. 269–280; reprint, Logic and algorithmic (Zurich, 1980) , Monographies de L’Enseignement Mathématique, vol. 30, Université de Genève, Geneva, pp. 381–392.Google Scholar