Article contents
Boolean simple groups and boolean simple rings
Published online by Cambridge University Press: 12 March 2014
Extract
Let 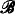 be a complete Boolean algebra and G a finite simple group in the Scott-Solovay
be a complete Boolean algebra and G a finite simple group in the Scott-Solovay 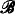 -valued model V
(
-valued model V
(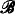 ) of set theory. If we observe G outside V
(
) of set theory. If we observe G outside V
(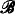 ), then we get a new group which is denoted by Ĝ. In general, Ĝ is not finite nor simple. Nevertheless Ĝ satisfies every property satisfied by a finite simple group with some translation. In this way, we can get a class of groups for which we can use a well-developed theory of the finite simple groups. We call Ĝ Boolean simple if G is simple in some V
(
), then we get a new group which is denoted by Ĝ. In general, Ĝ is not finite nor simple. Nevertheless Ĝ satisfies every property satisfied by a finite simple group with some translation. In this way, we can get a class of groups for which we can use a well-developed theory of the finite simple groups. We call Ĝ Boolean simple if G is simple in some V
(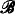 ). In the same way we define Boolean simple rings. The main purpose of this paper is a study of structures of Boolean simple groups and Boolean simple rings. As for Boolean simple rings, K. Eda previously constructed Boolean completion of rings with a certain condition. His construction is useful for our purpose.
). In the same way we define Boolean simple rings. The main purpose of this paper is a study of structures of Boolean simple groups and Boolean simple rings. As for Boolean simple rings, K. Eda previously constructed Boolean completion of rings with a certain condition. His construction is useful for our purpose.
The present work is a part of a series of systematic applications of Boolean valued method. The reader who is interested in this subject should consult with papers by Eda, Nishimura, Ozawa, and the author in the list of references.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1988
References
REFERENCES
- 2
- Cited by


