No CrossRef data available.
Automorphism groups of endomorphisms of 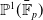 $\mathbb{P}^1 (\bar{\mathbb{F}}_p)$
$\mathbb{P}^1 (\bar{\mathbb{F}}_p)$
Published online by Cambridge University Press: 13 July 2022
Abstract
For any algebraically closed field K and any endomorphism f of
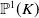 $\mathbb{P}^1(K)$
of degree at least 2, the automorphisms of f are the Möbius transformations that commute with f, and these form a finite subgroup of
$\mathbb{P}^1(K)$
of degree at least 2, the automorphisms of f are the Möbius transformations that commute with f, and these form a finite subgroup of
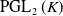 $\operatorname{PGL}_2(K)$
. In the moduli space of complex dynamical systems, the locus of maps with nontrivial automorphisms has been studied in detail and there are techniques for constructing maps with prescribed automorphism groups that date back to Klein. We study the corresponding questions when K is the algebraic closure
$\operatorname{PGL}_2(K)$
. In the moduli space of complex dynamical systems, the locus of maps with nontrivial automorphisms has been studied in detail and there are techniques for constructing maps with prescribed automorphism groups that date back to Klein. We study the corresponding questions when K is the algebraic closure
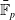 $\bar{\mathbb{F}}_p$
of a finite field. We use the classification of finite subgroups of
$\bar{\mathbb{F}}_p$
of a finite field. We use the classification of finite subgroups of
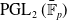 $\operatorname{PGL}_2(\bar{\mathbb{F}}_p)$
to show that every finite subgroup is realizable as an automorphism group. To construct examples, we use methods from modular invariant theory. Then, we calculate the locus of maps over
$\operatorname{PGL}_2(\bar{\mathbb{F}}_p)$
to show that every finite subgroup is realizable as an automorphism group. To construct examples, we use methods from modular invariant theory. Then, we calculate the locus of maps over
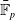 $\bar{\mathbb{F}}_p$
of degree 2 with nontrivial automorphisms, showing how the geometry and possible automorphism groups depend on the prime p.
$\bar{\mathbb{F}}_p$
of degree 2 with nontrivial automorphisms, showing how the geometry and possible automorphism groups depend on the prime p.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
Footnotes
Max Weinreich was supported by a National Science Foundation Graduate Research Fellowship under Grant No. 2040433.




