Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-684bc48f8b-g7stk Total loading time: 0.25 Render date: 2021-04-10T19:50:48.589Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
Compositio Mathematica Compositio Mathematica

Article contents

Counting resolutions of symplectic quotient singularities

Part of: Rings and algebras arising under various constructions Birational geometry Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  24 September 2015

Gwyn Bellamy
Gwyn Bellamy
Affiliation:
School of Mathematics and Statistics, University Gardens, University of Glasgow, GlasgowG12 8QW, UK email gwyn.bellamy@glasgow.ac.uk
Corresponding
E-mail address:
gwyn.bellamy@glasgow.ac.uk
Save pdf (0.49 mb)
Rights & Permissions[Opens in a new window]

Abstract

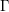Let ${\rm\Gamma}$ be a finite subgroup of 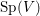$\text{Sp}(V)$. In this article we count the number of symplectic resolutions admitted by the quotient singularity 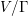$V/{\rm\Gamma}$. Our approach is to compare the universal Poisson deformation of the symplectic quotient singularity with the deformation given by the Calogero–Moser space. In this way, we give a simple formula for the number of 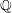$\mathbb{Q}$-factorial terminalizations admitted by the symplectic quotient singularity in terms of the dimension of a certain Orlik–Solomon algebra naturally associated to the Calogero–Moser deformation. This dimension is explicitly calculated for all groups 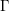${\rm\Gamma}$ for which it is known that 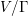$V/{\rm\Gamma}$ admits a symplectic resolution. As a consequence of our results, we confirm a conjecture of Ginzburg and Kaledin.

Keywords

symplectic resolutions symplectic reflection algebras Orlik–Solomon algebras

MSC classification

Primary: 14E15: Global theory and resolution of singularities
Secondary: 14E30: Minimal model program (Mori theory, extremal rays) 16S80: Deformations of rings 17B63: Poisson algebras
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 1 , January 2016 , pp. 99 - 114
Copyright
© The Author 2015 

References

Athanasiadis, C. A., Generalized Catalan numbers, Weyl groups and arrangements of hyperplanes, Bull. Lond. Math. Soc. 36 (2004), 294–302.CrossRefGoogle Scholar
Bellamy, G., On singular Calogero–Moser spaces, Bull. Lond. Math. Soc. 41 (2009), 315–326.CrossRefGoogle Scholar
Bellamy, G. and Martino, M., On the smoothness of centres of rational Cherednik algebras in positive characteristic, Glasg. Math. J. 55 (2013), 27–54.CrossRefGoogle Scholar
Bellamy, G. and Schedler, T., A new linear quotient of C4 admitting a symplectic resolution, Math. Z. 273 (2013), 753–769.CrossRefGoogle Scholar
Bellamy, G. and Schedler, T., On the (non)existence of symplectic resolutions for imprimitive symplectic reflection groups, Math. Res. Lett., to appear, arXiv:1309.3558.Google Scholar
BonnafĂ©, C. and Rouquier, R., Cellules de Calogero–Moser, Preprint (2013), arXiv:1302.2720.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system. I: The user language, J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Braden, T., Proudfoot, N. and Webster, B., Quantizations of conical symplectic resolutions I: Local and global structure, Preprint (2012), arXiv:1208.3863v3.Google Scholar
Crawley-Boevey, W., On the exceptional fibres of Kleinian singularities, Amer. J. Math. 122 (2000), 1027–1037.CrossRefGoogle Scholar
Donten-Bury, M. and Wiƛniewski, J. A., On 81 symplectic resolutions of a 4-dimensional quotient by a group of order 32, Preprint (2014), arXiv:1409.4204v3.Google Scholar
Etingof, P. and Ginzburg, V., Symplectic reflection algebras, Calogero–Moser space, and deformed Harish–Chandra homomorphism, Invent. Math. 147 (2002), 243–348.CrossRefGoogle Scholar
Fu, B., A survey on symplectic singularities and symplectic resolutions, Ann. Math. Blaise Pascal 13 (2006), 209–236.CrossRefGoogle Scholar
Ginzburg, V. and Kaledin, D., Poisson deformations of symplectic quotient singularities, Adv. Math. 186 (2004), 1–57.CrossRefGoogle Scholar
Gonzalez-Sprinberg, G. and Verdier, J.-L., Construction gĂ©omĂ©trique de la correspondance de McKay, Ann. Sci. Éc. Norm. SupĂ©r. (4) 16 (1984), 409–449; 1983.CrossRefGoogle Scholar
Gordon, I. G., Quiver varieties, category 𝓞 for rational Cherednik algebras, and Hecke algebras, Int. Math. Res. Pap. IMRP (2008), Art. ID rpn00669.Google Scholar
Hatcher, A., Algebraic topology (Cambridge University Press, Cambridge, 2002).Google Scholar
Kaledin, D., Dynkin diagrams and crepant resolutions of quotient singularities, Preprint (1999),arXiv:9903157.Google Scholar
Lehn, M., Namikawa, Y. and Sorger, Ch., Slodowy slices and universal Poisson deformations, Compositio Math. 148 (2012), 121–144.CrossRefGoogle Scholar
Lehn, M. and Sorger, C., A symplectic resolution for the binary tetrahedral group, SĂ©min. Congr. 25 (2010), 427–433.Google Scholar
Losev, I., Completions of symplectic reflection algebras, Selecta Math. (N.S.) 18 (2012), 179–251.CrossRefGoogle Scholar
Losev, I., Isomorphisms of quantizations via quantization of resolutions, Adv. Math. 231 (2012), 1216–1270.CrossRefGoogle Scholar
Martino, M., Stratifications of Marsden-Weinstein reductions for representations of quivers and deformations of symplectic quotient singularities, Math. Z. 258 (2008), 1–28.CrossRefGoogle Scholar
Namikawa, Y., A note on symplectic singularities, Preprint (2001), arXiv:0101028.Google Scholar
Namikawa, Y., Flops and Poisson deformations of symplectic varieties, Publ. Res. Inst. Math. Sci. 44 (2008), 259–314.CrossRefGoogle Scholar
Namikawa, Y., Poisson deformations of affine symplectic varieties, II, Kyoto J. Math. 50 (2010), 727–752.CrossRefGoogle Scholar
Namikawa, Y., Poisson deformations of affine symplectic varieties, Duke Math. J. 156 (2011), 51–85.CrossRefGoogle Scholar
Namikawa, Y., Poisson deformations and birational geometry, J. Math. Sci. Univ. Tokyo. 22 (2015), 339–359.Google Scholar
Orlik, P. and Terao, H., Arrangements of hyperplanes, Grundlehren der Mathematischen Wissenschaften, vol. 300 (Springer, Berlin, 1992).CrossRefGoogle Scholar
Slodowy, P., Four lectures on simple groups and singularities, Communications of the Mathematical Institute, Rijksuniversiteit Utrecht, vol. 11 (Rijksuniversiteit Utrecht, Mathematical Institute, Utrecht, 1980).CrossRefGoogle Scholar

Altmetric attention score

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 108 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 10th April 2021. This data will be updated every 24 hours.

Access Access
5
Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Counting resolutions of symplectic quotient singularities
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Counting resolutions of symplectic quotient singularities
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Counting resolutions of symplectic quotient singularities
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *