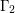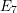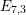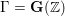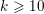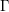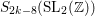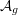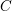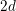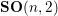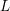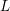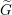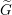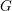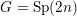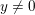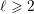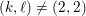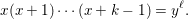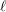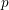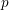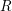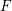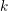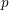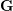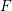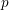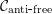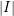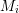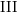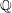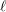Research Article
Double affine Hecke algebras and generalized Jones polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1333-1384
-
- Article
-
- You have access
- Export citation
Quivers with loops and generalized crystals
- Part of:
-
- Published online by Cambridge University Press:
- 20 July 2016, pp. 1999-2040
-
- Article
-
- You have access
- Export citation
The Chowla–Selberg formula for abelian CM fields and Faltings heights
- Part of:
-
- Published online by Cambridge University Press:
- 24 September 2015, pp. 445-476
-
- Article
-
- You have access
- Export citation
Cusp forms on the exceptional group of type
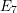 $E_{7}$
$E_{7}$
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2015, pp. 223-254
-
- Article
-
- You have access
- Export citation
Equidistribution of primitive rational points on expanding horospheres
-
- Published online by Cambridge University Press:
- 09 November 2015, pp. 667-692
-
- Article
-
- You have access
- Export citation
On the Oort conjecture for Shimura varieties of unitary and orthogonal types
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2016, pp. 889-917
-
- Article
-
- You have access
- Export citation
Arithmetic of positive characteristic
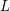 $L$-series values in Tate algebras
$L$-series values in Tate algebras
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2015, pp. 1-61
-
- Article
-
- You have access
- Export citation
Ramification conjecture and Hirzebruch’s property of line arrangements
- Part of:
-
- Published online by Cambridge University Press:
- 25 October 2016, pp. 2443-2460
-
- Article
-
- You have access
- Export citation
Curvature and the c-projective mobility of Kähler metrics with hamiltonian 2-forms
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1555-1575
-
- Article
-
- You have access
- Export citation
Non-contractible periodic orbits in Hamiltonian dynamics on closed symplectic manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 17 June 2016, pp. 1777-1799
-
- Article
-
- You have access
- Export citation
The equidistribution of lattice shapes of rings of integers in cubic, quartic, and quintic number fields
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2016, pp. 1111-1120
-
- Article
-
- You have access
- Export citation
Weak solutions of complex Hessian equations on compact Hermitian manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2016, pp. 2221-2248
-
- Article
-
- You have access
- Export citation
Compactifications of reductive groups as moduli stacks of bundles
- Part of:
-
- Published online by Cambridge University Press:
- 18 August 2015, pp. 62-98
-
- Article
-
- You have access
- Export citation
On a lifting problem of L-packets
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1800-1850
-
- Article
-
- You have access
- Export citation
Rational points on Erdős–Selfridge superelliptic curves
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 2249-2254
-
- Article
-
- You have access
- Export citation
Degree bounds on homology and a conjecture of Derksen
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2041-2049
-
- Article
-
- You have access
- Export citation
Upper semi-continuity of the Hilbert–Kunz multiplicity
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2016, pp. 477-488
-
- Article
-
- You have access
- Export citation
The pro-
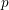 $p$-Iwahori Hecke algebra of a reductive
$p$-Iwahori Hecke algebra of a reductive 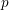 $p$-adic group I
$p$-adic group I
- Part of:
-
- Published online by Cambridge University Press:
- 23 October 2015, pp. 693-753
-
- Article
-
- You have access
- Export citation
Rigidity of free product von Neumann algebras
- Part of:
-
- Published online by Cambridge University Press:
- 17 November 2016, pp. 2461-2492
-
- Article
-
- You have access
- Export citation
Level raising mod 2 and arbitrary 2-Selmer ranks
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 1576-1608
-
- Article
-
- You have access
- Export citation