Article contents
On a lifting problem of L-packets
Published online by Cambridge University Press: 14 July 2016
Abstract
Let 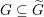 $G\subseteq \widetilde{G}$ be two quasisplit connected reductive groups over a local field of characteristic zero and having the same derived group. Although the existence of L-packets is still conjectural in general, it is believed that the L-packets of
$G\subseteq \widetilde{G}$ be two quasisplit connected reductive groups over a local field of characteristic zero and having the same derived group. Although the existence of L-packets is still conjectural in general, it is believed that the L-packets of 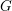 $G$ should be the restriction of those of
$G$ should be the restriction of those of 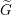 $\widetilde{G}$. Motivated by this, we hope to construct the L-packets of
$\widetilde{G}$. Motivated by this, we hope to construct the L-packets of  $\widetilde{G}$ from those of
$\widetilde{G}$ from those of 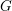 $G$. The primary example in our mind is when
$G$. The primary example in our mind is when 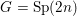 $G=\text{Sp}(2n)$, whose L-packets have been determined by Arthur [The endoscopic classification of representations: orthogonal and symplectic groups, Colloquium Publications, vol. 61 (American Mathematical Society, Providence, RI, 2013)], and
$G=\text{Sp}(2n)$, whose L-packets have been determined by Arthur [The endoscopic classification of representations: orthogonal and symplectic groups, Colloquium Publications, vol. 61 (American Mathematical Society, Providence, RI, 2013)], and 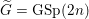 $\widetilde{G}=\text{GSp}(2n)$. As a first step, we need to consider some well-known conjectural properties of L-packets. In this paper, we show how they can be deduced from the conjectural endoscopy theory. As an application, we obtain some structural information about L-packets of
$\widetilde{G}=\text{GSp}(2n)$. As a first step, we need to consider some well-known conjectural properties of L-packets. In this paper, we show how they can be deduced from the conjectural endoscopy theory. As an application, we obtain some structural information about L-packets of 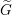 $\widetilde{G}$ from those of
$\widetilde{G}$ from those of 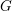 $G$.
$G$.
- Type
- Research Article
- Information
- Copyright
- © The Author 2016
References
- 12
- Cited by


