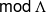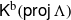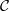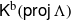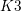Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 369
Cluster algebras IV: Coefficients
-
- Published online by Cambridge University Press:
- 19 January 2007, pp. 112-164
-
- Article
-
- You have access
- Export citation
- Cited by 232
 $\tau $-tilting theory
$\tau $-tilting theory
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2013, pp. 415-452
-
- Article
-
- You have access
- Export citation
- Cited by 192
Derivation and double shuffle relations for multiple zeta values
-
- Published online by Cambridge University Press:
- 13 March 2006, pp. 307-338
-
- Article
-
- You have access
- Export citation
- Cited by 184
Gromov–Witten theory and Donaldson–Thomas theory, I
-
- Published online by Cambridge University Press:
- 25 September 2006, pp. 1263-1285
-
- Article
-
- You have access
- Export citation
- Cited by 173
the stable derived category of a noetherian scheme
-
- Published online by Cambridge University Press:
- 01 September 2005, pp. 1128-1162
-
- Article
-
- You have access
- Export citation
- Cited by 151
Isocrystals with additional structure. II
-
- Published online by Cambridge University Press:
- 04 December 2007, pp. 255-339
-
- Article
-
- You have access
- Export citation
- Cited by 140
Cluster structures for 2-Calabi–Yau categories and unipotent groups
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2009, pp. 1035-1079
-
- Article
-
- You have access
- Export citation
- Cited by 136
The classification of triangulated subcategories
-
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1-27
-
- Article
-
- You have access
- Export citation
- Cited by 131
Asymptotic Behaviour of the Castelnuovo-Mumford Regularity
-
- Published online by Cambridge University Press:
- 04 December 2007, pp. 243-261
-
- Article
-
- You have access
- Export citation
- Cited by 121
Geometry of the Moment Map for Representations of Quivers
-
- Published online by Cambridge University Press:
- 04 December 2007, pp. 257-293
-
- Article
-
- You have access
- Export citation
- Cited by 112
Modular operads
-
- Published online by Cambridge University Press:
- 04 December 2007, pp. 65-125
-
- Article
-
- You have access
- Export citation
- Cited by 104
Reconstruction of a Variety from the Derived Category and Groups of Autoequivalences
-
- Published online by Cambridge University Press:
- 04 December 2007, pp. 327-344
-
- Article
-
- You have access
- Export citation
- Cited by 104
Special Cubic Fourfolds
-
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1-23
-
- Article
-
- You have access
- Export citation
- Cited by 103
A Feynman integral via higher normal functions
- Part of:
-
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2329-2375
-
- Article
-
- You have access
- Export citation
- Cited by 95
The universal Euler characteristic for varieties of characteristic zero
-
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1011-1032
-
- Article
-
- You have access
- Export citation
- Cited by 94
Combinatorial Hopf algebras and generalized Dehn–Sommerville relations
-
- Published online by Cambridge University Press:
- 13 January 2006, pp. 1-30
-
- Article
-
- You have access
- Export citation
- Cited by 85
Noncrossing partitions and representations of quivers
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1533-1562
-
- Article
-
- You have access
- Export citation
- Cited by 85
Gromov–Witten theory and Donaldson–Thomas theory, II
-
- Published online by Cambridge University Press:
- 25 September 2006, pp. 1286-1304
-
- Article
-
- You have access
- Export citation
- Cited by 82
Restricting linear syzygies: algebra and geometry
-
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1460-1478
-
- Article
-
- You have access
- Export citation
- Cited by 80
Wild non-abelian Hodge theory on curves
-
- Published online by Cambridge University Press:
- 04 December 2007, pp. 179-204
-
- Article
-
- You have access
- Export citation