Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
EnglishFrançais
Compositio Mathematica Compositio Mathematica

Article contents

$\tau $ -tilting theory

Part of: Abelian categories Modules, bimodules and ideals Representation theory of rings and algebras

Published online by Cambridge University Press:  03 December 2013

Takahide Adachi ,
Osamu Iyama  and
Idun Reiten
Takahide Adachi
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku, Nagoya 464-8602, Japan email m09002b@math.nagoya-u.ac.jp
Osamu Iyama
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku, Nagoya 464-8602, Japan email iyama@math.nagoya-u.ac.jp
Idun Reiten
Affiliation:
Department of Mathematical Sciences, Norges teknisk-naturvitenskapelige universitet, 7491 Trondheim, Norway email idunr@math.ntnu.no
Corresponding
E-mail address:
m09002b@math.nagoya-u.ac.jp
iyama@math.nagoya-u.ac.jp
idunr@math.ntnu.no
Save pdf (0.96 mb)
Rights & Permissions[Opens in a new window]

Abstract

The aim of this paper is to introduce $\tau $ -tilting theory, which ‘completes’ (classical) tilting theory from the viewpoint of mutation. It is well known in tilting theory that an almost complete tilting module for any finite-dimensional algebra over a field 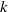$k$ is a direct summand of exactly one or two tilting modules. An important property in cluster-tilting theory is that an almost complete cluster-tilting object in a 2-CY triangulated category is a direct summand of exactly two cluster-tilting objects. Reformulated for path algebras 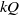$kQ$ , this says that an almost complete support tilting module has exactly two complements. We generalize (support) tilting modules to what we call (support) $\tau $ -tilting modules, and show that an almost complete support $\tau $ -tilting module has exactly two complements for any finite-dimensional algebra. For a finite-dimensional 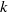$k$ -algebra 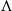$\Lambda $ , we establish bijections between functorially finite torsion classes in 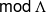$ \mathsf{mod} \hspace{0.167em} \Lambda $ , support $\tau $ -tilting modules and two-term silting complexes in 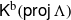${ \mathsf{K} }^{\mathrm{b} } ( \mathsf{proj} \hspace{0.167em} \Lambda )$ . Moreover, these objects correspond bijectively to cluster-tilting objects in 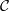$ \mathcal{C} $ if 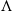$\Lambda $ is a 2-CY tilted algebra associated with a 2-CY triangulated category 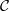$ \mathcal{C} $ . As an application, we show that the property of having two complements holds also for two-term silting complexes in 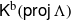${ \mathsf{K} }^{\mathrm{b} } ( \mathsf{proj} \hspace{0.167em} \Lambda )$ .

Keywords

τ-tilting module tilting module torsion class silting complex cluster-tilting object E-invariant

MSC classification

Secondary: 16D20: Bimodules 16G20: Representations of quivers and partially ordered sets 18E40: Torsion theories, radicals
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 3 , March 2014 , pp. 415 - 452
Copyright
© The Author(s) 2013 

References

Abe, H., Tilting modules arising from two-term tilting complexes, Preprint (2011), arXiv:1104.0627.Google Scholar
Adachi, T., $\tau $-tilting modules over Nakayama algebras, Preprint (2013), arXiv:1309.2216.Google Scholar
Aihara, T., Tilting-connected symmetric algebras, Algebr. Represent. Theory 16 (2013), 873–894.CrossRefGoogle Scholar
Aihara, T. and Iyama, O., Silting mutation in triangulated categories, J. Lond. Math. Soc. 85 (2012), 633–668.CrossRefGoogle Scholar
Amiot, C., Cluster categories for algebras of global dimension 2 and quiver with potential, Ann. Inst. Fourier 59 (2009), 2525–2590.CrossRefGoogle Scholar
Assem, I., Simson, D. and Skowronski, A., Elements of the representation theory of associative algebras, Vol. 65 (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Auslander, M., Platzeck, M. I. and Reiten, I., Coxeter functions without diagrams, Trans. Amer. Math. Soc. 250 (1979), 1–12.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., Representation theory of Artin algebras III: almost split sequences, Comm. Algebra 3 (1975), 239–294.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., Representation theory of Artin algebras V: methods for computing almost split sequences and irreducible morphisms, Comm. Algebra 5 (1977), 519–554.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., Modules determined by their composition factors, Illinois J. Math. 29 (1985), 280–301.Google Scholar
Auslander, M. and Reiten, I., Applications of contravariantly finite subcategories, Adv. Math. 86 (1991), 111–152.CrossRefGoogle Scholar
Auslander, M., Reiten, I. and Smalø, S. O., Representation theory of Artin algebras, Cambridge Studies in Advanced Mathematics, vol. 36 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Auslander, M. and Smalø, S. O., Almost split sequences in subcategories, J. Algebra 69 (1981), 426–454. Addendum: J. Algebra 71 (1981), 592–594.CrossRefGoogle Scholar
Bernstein, I. N., Gelfand, I. M. and Ponomarev, V. A., Coxeter functors and Gabriel’s theorem, Russian Math. Surveys 28 (1973), 17–32.CrossRefGoogle Scholar
Bongartz, K., Tilted algebras, in Proc. ICRA III (Puebla 1980), Lecture Notes in Mathematics, vol. 903 (Springer, New York, 1981), 26–38.Google Scholar
Brenner, S. and Butler, M. C. R., Generalization of the Bernstein–Gelfand–Ponomarev reflection functors, Lecture Notes in Mathematics, vol. 839 (Springer, New York, 1980), 103–169.Google Scholar
Buan, A., Iyama, O., Reiten, I. and Smith, D., Mutation of cluster-tilting objects and potentials, Amer. J. Math. 133 (2011), 835–887.CrossRefGoogle Scholar
Buan, A. B., Marsh, R., Reineke, M., Reiten, I. and Todorov, G., Tilting theory and cluster combinatorics, Adv. Math. 204 (2006), 572–618.CrossRefGoogle Scholar
Buan, A. B., Marsh, R. and Reiten, I., Denominators of cluster variables, J. Lond. Math. Soc. (2) 79 (2006), 589–611.CrossRefGoogle Scholar
Buan, A. B., Marsh, R. and Reiten, I., Cluster-tilted algebras, Trans. Amer. Math. Soc. 359 (2007), 323–332.CrossRefGoogle Scholar
Buan, A. B., Marsh, R., Reiten, I. and Todorov, G., Clusters and seeds in acyclic cluster algebras, Proc. Amer. Math. Soc. 135 (2007), 3049–3060; with an appendix coauthored in addition by P. Caldero and B. Keller.CrossRefGoogle Scholar
Buan, A. B., Reiten, I. and Thomas, H., Three kinds of mutation, J. Algebra 339 (2011), 97–113.CrossRefGoogle Scholar
Caldero, P. and Keller, B., From triangulated categories to cluster algebras II, Ann. Sci Éc. Norm. Supér. (4) 39 (2006), 983–1009.CrossRefGoogle Scholar
Cerulli Irelli, G., Labardini-Fragoso, D. and Schröer, J., Caldero–Chapoton algebras, Trans. Amer. Math. Soc., to appear, arXiv:1208.3310.Google Scholar
Dehy, R. and Keller, B., On the combinatorics of rigid objects in 2-Calabi–Yau categories, Int. Math. Res. Not. IMRN (2008), Art. ID rnn029.Google Scholar
Derksen, H. and Fei, J., General presentations of algebras, Preprint (2009), arXiv:0911.4913.Google Scholar
Derksen, H., Weyman, J. and Zelevinsky, A., Quivers with potentials and their representations II: applications to cluster algebras, J. Amer. Math. Soc. 23 (2010), 749–790.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras IV: coefficients, Compositio Math. 143 (2007), 112–164.CrossRefGoogle Scholar
Fu, C. and Liu, P., Lifting to cluster-tilting objects in 2-Calabi–Yau triangulated categories, Comm. Algebra 37 (2009), 2410–2418.CrossRefGoogle Scholar
Happel, D., Triangulated categories in the representation theory of finite-dimensional algebras, London Mathematical Society Lecture Note Series, vol. 119 (Cambridge University Press, Cambridge, 1988).CrossRefGoogle Scholar
Happel, D. and Ringel, C. M., Tilted algebras, Trans. Amer. Math. Soc. 274 (1982), 399–443.CrossRefGoogle Scholar
Happel, D. and Unger, L., Almost complete tilting modules, Proc. Amer. Math. Soc. 107 (1989), 603–610.CrossRefGoogle Scholar
Happel, D. and Unger, L., On a partial order of tilting modules, Algebr. Represent. Theory 8 (2005), 147–156.CrossRefGoogle Scholar
Hoshino, M., Tilting modules and torsion theories, Bull. Lond. Math. Soc. 14 (1982), 334–336.CrossRefGoogle Scholar
Hoshino, M., Kato, Y. and Miyachi, J., On $t$-structures and torsion theories induced by compact objects, J. Pure Appl. Algebra 167 (2002), 15–35.CrossRefGoogle Scholar
Ingalls, C. and Thomas, H., Noncrossing partitions and representations of quivers, Compositio Math. 145 (2009), 1533–1562.CrossRefGoogle Scholar
Iyama, O. and Yoshino, Y., Mutations in triangulated categories and rigid Cohen–Macaulay modules, Invent. Math. 172 (2008), 117–168.CrossRefGoogle Scholar
Jasso, G., Reduction of $\tau $-tilting modules and torsion pairs, Preprint (2013), arXiv:1302.2709.Google Scholar
Keller, B. and Reiten, I., Cluster-tilted algebras are Gorenstein and stably Calabi–Yau, Adv. Math. 211 (2007), 123–151.CrossRefGoogle Scholar
Keller, B. and Vossieck, D., Aisles in derived categories, in Deuxieme Contact Franco-Belge en Algebre (Faulx-les-Thombes, 1987), Bull. Soc. Math. Belg. 40 (1988), 239–253.Google Scholar
König, S. and Yang, D., Silting objects, simple-minded collections, $t$-structures and co- $t$-structures for finite-dimensional algebras, Preprint (2012), arXiv:1203.5657.Google Scholar
Miyashita, Y., Tilting modules of finite projective dimension, Math. Z. 193 (1986), 113–146.CrossRefGoogle Scholar
Mizuno, Y., Classifying $\tau $-tilting modules over preprojective algebras of Dynkin type, Preprint (2013), arXiv:1304.0667.Google Scholar
Palu, Y., Cluster characters for 2-Calabi–Yau triangulated categories, Ann. Inst. Fourier (Grenoble) 58 (2008), 2221–2248.CrossRefGoogle Scholar
Riedtmann, C. and Schofield, A., On a simplicial complex associated with tilting modules, Comment. Math. Helv. 66 (1991), 70–78.CrossRefGoogle Scholar
Rickard, J., Morita theory for derived categories, J. Lond. Math. Soc. (2) 39 (1989), 436–456.CrossRefGoogle Scholar
Ringel, C. M., Some remarks concerning tilting modules and tilted algebras. Origin. Relevance. Future, in Handbook of tilting theory, London Mathematical Society Lecture Note Series, vol. 332 (Cambridge University Press, 2007), 49–104.Google Scholar
Skowronski, A., Regular Auslander–Reiten components containing directing modules, Proc. Amer. Math. Soc. 120 (1994), 19–26.CrossRefGoogle Scholar
Smalø, S. O., Torsion theory and tilting modules, Bull. Lond. Math. Soc. 16 (1984), 518–522.CrossRefGoogle Scholar
Smith, D., On tilting modules over cluster-tilted algebras, Illinois J. Math. 52 (2008), 1223–1247.Google Scholar
Unger, L., Schur modules over wild, finite-dimensional path algebras with three simple modules, J. Pure Appl. Algebra 64 (1990), 205–222.CrossRefGoogle Scholar
Zhang, X., $\tau $-rigid modules for algebras with radical square zero, Preprint (2012), arXiv:1211.5622.Google Scholar
Zhou, Y. and Zhu, B., Maximal rigid subcategories in 2-Calabi–Yau triangulated categories, J. Algebra 348 (2011), 49–60.CrossRefGoogle Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 1
Total number of PDF views: 933 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 28th January 2021. This data will be updated every 24 hours.

Access
99 Cited by
Hostname: page-component-898fc554b-t4g97 Total loading time: 0.371 Render date: 2021-01-28T03:51:20.608Z Query parameters: { "hasAccess": "1", "openAccess": "0", "isLogged": "0", "lang": "en" } Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false }

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

$\tau $ -tilting theory
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

$\tau $ -tilting theory
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

$\tau $ -tilting theory
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *