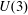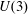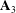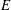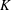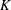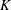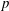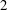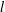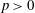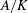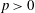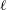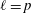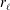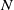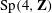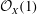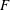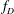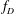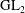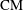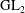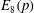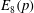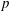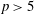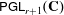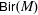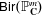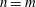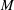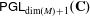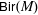Research Article
Endoscopy and cohomology growth on
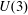 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}U(3)$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}U(3)$
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2014, pp. 903-910
-
- Article
-
- You have access
- Export citation
Counting imaginary quadratic points via universal torsors
- Part of:
-
- Published online by Cambridge University Press:
- 25 July 2014, pp. 1631-1678
-
- Article
-
- You have access
- Export citation
Unitary cycles on Shimura curves and the Shimura lift II
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 1963-2002
-
- Article
-
- You have access
- Export citation
A Markov model for Selmer ranks in families of twists
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1077-1106
-
- Article
-
- You have access
- Export citation
Linear independence of monomials of multizeta values in positive characteristic
- Part of:
-
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1789-1808
-
- Article
-
- You have access
- Export citation
Modularity of nearly ordinary 2-adic residually dihedral Galois representations
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2014, pp. 1235-1346
-
- Article
-
- You have access
- Export citation
Hopfological algebra
- Part of:
-
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1-45
-
- Article
-
- You have access
- Export citation
The
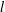 $l$-parity conjecture for abelian varieties over function fields of characteristic
$l$-parity conjecture for abelian varieties over function fields of characteristic 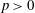 $p>0$
$p>0$
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2014, pp. 507-522
-
- Article
-
- You have access
- Export citation
Stable maps and stable quotients
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1457-1481
-
- Article
-
- You have access
- Export citation
Applications du théorème d’Ax–Lindemann hyperbolique
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2013, pp. 175-190
-
- Article
-
- You have access
- Export citation
Thin monodromy in Sp(4)
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2014, pp. 333-343
-
- Article
-
- You have access
- Export citation
Level-raising and symmetric power functoriality, I
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2014, pp. 729-748
-
- Article
-
- You have access
- Export citation
On a completed generating function of locally harmonic Maass forms
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2014, pp. 749-762
-
- Article
-
- You have access
- Export citation
Galois representations attached to automorphic forms on
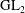 ${\rm GL}_2$ over
${\rm GL}_2$ over 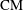 ${\rm CM}$ fields
${\rm CM}$ fields
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2014, pp. 523-567
-
- Article
-
- You have access
- Export citation
Refined abelian Stark conjectures and the equivariant leading term conjecture of Burns
- Part of:
-
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1809-1835
-
- Article
-
- You have access
- Export citation
Galois representations associated to holomorphic limits of discrete series
- Part of:
-
- Published online by Cambridge University Press:
- 26 November 2013, pp. 191-228
-
- Article
-
- You have access
- Export citation
Rational rigidity for
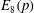 ${E}_{8}(p)$
${E}_{8}(p)$
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1679-1702
-
- Article
-
- You have access
- Export citation
Laurent polynomials, GKZ-hypergeometric systems and mixed Hodge modules
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2014, pp. 911-941
-
- Article
-
- You have access
- Export citation
Corrigendum
Corrigendum: Elliptic curves with a given number of points over finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1347-1348
-
- Article
-
- You have access
- Export citation
Research Article
Morphisms between Cremona groups, and characterization of rational varieties
- Part of:
-
- Published online by Cambridge University Press:
- 25 June 2014, pp. 1107-1124
-
- Article
-
- You have access
- Export citation