Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Harris, Michael
Lan, Kai-Wen
Taylor, Richard
and
Thorne, Jack
2016.
On the rigid cohomology of certain Shimura varieties.
Research in the Mathematical Sciences,
Vol. 3,
Issue. 1,
Pilloni, Vincent
and
Stroh, Benoît
2016.
Cohomologie cohérente et représentations Galoisiennes.
Annales mathématiques du Québec,
Vol. 40,
Issue. 1,
p.
167.
Caraiani, Ana
and
Scholze, Peter
2017.
On the generic part of the cohomology of compact unitary Shimura varieties.
Annals of Mathematics,
Vol. 186,
Issue. 3,
Goldring, Wushi
and
Nicole, Marc-Hubert
2017.
The μ-ordinary Hasse invariant of\break unitary Shimura varieties.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2017,
Issue. 728,
p.
137.
Calegari, Frank
and
Geraghty, David
2018.
Modularity lifting beyond the Taylor–Wiles method.
Inventiones mathematicae,
Vol. 211,
Issue. 1,
p.
297.
Hernandez, Valentin
2019.
Families of Picard modular forms and an application to the Bloch–Kato conjecture.
Compositio Mathematica,
Vol. 155,
Issue. 7,
p.
1327.
Chenevier, Gaëtan
and
Lannes, Jean
2019.
Automorphic Forms and Even Unimodular Lattices.
p.
191.
Calegari, Frank
and
Geraghty, David
2020.
Minimal modularity lifting for nonregular symplectic representations.
Duke Mathematical Journal,
Vol. 169,
Issue. 5,
Grbac, Neven
and
Schwermer, Joachim
2021.
Eisenstein series for rank one unitary groups and some cohomological applications.
Advances in Mathematics,
Vol. 376,
Issue. ,
p.
107438.
Gehrmann, Lennart
and
Rosso, Giovanni
2022.
Big principal series, -adic families and -invariants.
Compositio Mathematica,
Vol. 158,
Issue. 2,
p.
409.
Fakhruddin, Najmuddin
and
Pilloni, Vincent
2023.
HECKE OPERATORS AND THE COHERENT COHOMOLOGY OF SHIMURA VARIETIES.
Journal of the Institute of Mathematics of Jussieu,
Vol. 22,
Issue. 1,
p.
1.
A’Campo, Lambert
2024.
Rigidity of Automorphic Galois Representations Over CM Fields.
International Mathematics Research Notices,
Vol. 2024,
Issue. 6,
p.
4541.
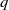 $q$-expansions.
$q$-expansions.



