No CrossRef data available.
Article contents
Abelian Quadratic Forms
Published online by Cambridge University Press: 20 November 2018
Extract
Hermite [4] in the course of his investigations on the transformation
theory of abelian functions, introduced the notion of abelian quadratic
forms. They are quadratic forms whose matrices  of orders 2n, satisfy
of orders 2n, satisfy
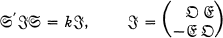
where k ≠ 0 is a real number, and  is the unit matrix of order n. Laguerre [7] and, more systematically, Cotty [3] developed an arithmetical theory of abelian forms in four variables.
is the unit matrix of order n. Laguerre [7] and, more systematically, Cotty [3] developed an arithmetical theory of abelian forms in four variables.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1952


