Research Article
Sur Un Problème De Configurations Et Sur Les Fractions Continues
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 2-25
-
- Article
-
- You have access
- Export citation
Zeta Functions on the Unitary Sphere
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 26-30
-
- Article
-
- You have access
- Export citation
The Homomorphic Mapping of Certain Matric Algebras onto Rings of Diagonal Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 31-42
-
- Article
-
- You have access
- Export citation
Contributions to Noncommutative Ideal Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 43-57
-
- Article
-
- You have access
- Export citation
Note on Normal Decimals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 58-63
-
- Article
-
- You have access
- Export citation
On Products of Sets of Group Elements
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 64-66
-
- Article
-
- You have access
- Export citation
The Fourier Coefficients of the Modular Function λ(τ)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 67-80
-
- Article
-
- You have access
- Export citation
Axioms for Elliptic Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 81-92
-
- Article
-
- You have access
- Export citation
On the Geometry of Lineal Elements on A Sphere, Euclidean Kinematics, and Elliptic Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 93-110
-
- Article
-
- You have access
- Export citation
On the Property С and A Problem of Hausdorff
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 111-116
-
- Article
-
- You have access
- Export citation
A Remark on the Existence of a Denumerable Base for a Family of Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 117-119
-
- Article
-
- You have access
- Export citation
An Extension of Meyer's Theorem on Indefinite Ternary Quadratic Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 120-128
-
- Article
-
- You have access
- Export citation
On Simple Alternative Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 129-135
-
- Article
-
- You have access
- Export citation
A Symmetric Proof of the Riemann-Roch Theorem, and a New Form of the Unit Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 136-148
-
- Article
-
- You have access
- Export citation
Iterated Transforms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-161
-
- Article
-
- You have access
- Export citation
A Theory of Normal Chains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 162-188
-
- Article
-
- You have access
- Export citation
Quelques Remarques Sur La Généralisation Du Scalaire De Courbure Et Du Scalaire Principal
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 189-197
-
- Article
-
- You have access
- Export citation
A Closure Criterion for Orthogonal Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 198-203
-
- Article
-
- You have access
- Export citation
On Surfaces Whose Canonical System is Hyperelliptic
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 204-221
-
- Article
-
- You have access
- Export citation
Some Theorems on Difference Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 222-226
-
- Article
-
- You have access
- Export citation

 , whereas in the present paper it is proposed to define one on the unitary sphere
, whereas in the present paper it is proposed to define one on the unitary sphere  where
where 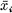 their complex conjugates. Following E. Cartan, harmonics on the unitary sphere are defined and then a zeta function formed just as in the case of a real sphere. The unitary sphere is seen to behave like an even-dimensional closed manifold, since results similar to the ones proved by the author and A. Pleijel [
their complex conjugates. Following E. Cartan, harmonics on the unitary sphere are defined and then a zeta function formed just as in the case of a real sphere. The unitary sphere is seen to behave like an even-dimensional closed manifold, since results similar to the ones proved by the author and A. Pleijel [
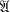 = {A
= {A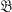 = {B
= {B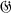 of finite order g. We define
of finite order g. We define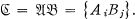
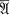 ,
, 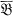 , … the sets of elements of
, … the sets of elements of 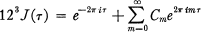
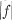 ) Ω, the g.c.d. of the 2-rowed minors of
) Ω, the g.c.d. of the 2-rowed minors of 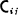 where
where  . The elements
. The elements  ,
, 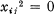 for every
for every 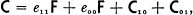 . The multiplication table of
. The multiplication table of 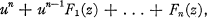




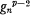 since the adjoint system of the canonical system is its double, so that the canonical series on a curve of the canonical system is its characteristic series doubled.
since the adjoint system of the canonical system is its double, so that the canonical series on a curve of the canonical system is its characteristic series doubled.