Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Du Val, Patrick
1953.
Regular Surfaces of Genus Two: Part I.
Canadian Journal of Mathematics,
Vol. 5,
Issue. ,
p.
216.
Beltrametti, M. C.
and
Sommese, A. J.
2001.
On the bicanonical map of a surface section of a threefold.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 71,
Issue. 1,
p.
269.
Ciliberto, Ciro
and
Lopes, Margarida Mendes
2002.
On surfaces with pg=q=2 and non-birational bicanonical maps.
advg,
Vol. 2,
Issue. 3,
p.
281.
Pardini, Rita
2003.
The classification of double planes of general type with K2=8 and pg=0.
Journal of Algebra,
Vol. 259,
Issue. 1,
p.
95.
Polizzi, Francesco
2005.
Surfaces of general type with 𝑝_{𝑔}=𝑞=1,𝐾²=8 and bicanonical map of degree 2.
Transactions of the American Mathematical Society,
Vol. 358,
Issue. 2,
p.
759.
Bauer, Ingrid C.
Catanese, Fabrizio
and
Pignatelli, Roberto
2006.
Global Aspects of Complex Geometry.
p.
1.
Calabri, Alberto
Ciliberto, Ciro
and
Mendes Lopes, Margarida
2006.
Numerical Godeaux surfaces with an involution.
Transactions of the American Mathematical Society,
Vol. 359,
Issue. 4,
p.
1605.
Borrelli, Giuseppe
2007.
The classification of surfaces of general type with nonbirational bicanonical map.
Journal of Algebraic Geometry,
Vol. 16,
Issue. 4,
p.
625.
Beltrametti, M. C.
Ciliberto, C.
Lanteri, A.
and
Sommese, A. J.
2007.
On the Birationality of the Bicanonical Map of a Surface Section of a Threefold.
Communications in Algebra,
Vol. 35,
Issue. 5,
p.
1627.
Werner, Caryn
2010.
On Surfaces withpg= 0 andK2= 5.
Canadian Mathematical Bulletin,
Vol. 53,
Issue. 4,
p.
746.
Rito, Carlos
2015.
Some bidouble planes with pg= q = 0 and 4 ≤ K2≤ 7.
International Journal of Mathematics,
Vol. 26,
Issue. 05,
p.
1550035.
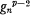 since the adjoint system of the canonical system is its double, so that the canonical series on a curve of the canonical system is its characteristic series doubled.
since the adjoint system of the canonical system is its double, so that the canonical series on a curve of the canonical system is its characteristic series doubled.



