Article contents
Zeta Functions on the Unitary Sphere
Published online by Cambridge University Press: 20 November 2018
Extract
In an earlier paper [5], the author defined a zeta function on the real sphere  , whereas in the present paper it is proposed to define one on the unitary sphere
, whereas in the present paper it is proposed to define one on the unitary sphere  where xi's are complex numbers and
where xi's are complex numbers and 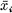 their complex conjugates. Following E. Cartan, harmonics on the unitary sphere are defined and then a zeta function formed just as in the case of a real sphere. The unitary sphere is seen to behave like an even-dimensional closed manifold, since results similar to the ones proved by the author and A. Pleijel [6] for closed manifolds (of even dimensions) are observed here also.
their complex conjugates. Following E. Cartan, harmonics on the unitary sphere are defined and then a zeta function formed just as in the case of a real sphere. The unitary sphere is seen to behave like an even-dimensional closed manifold, since results similar to the ones proved by the author and A. Pleijel [6] for closed manifolds (of even dimensions) are observed here also.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1952
References
- 9
- Cited by




