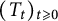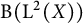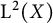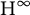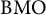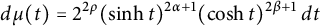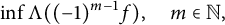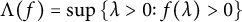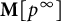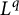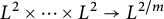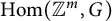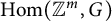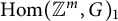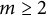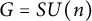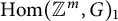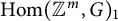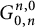Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
Disoriented homology and double branched covers
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2022, pp. 731-773
-
- Article
- Export citation
Dilations of Markovian semigroups of measurable Schur multipliers
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2023, pp. 774-797
-
- Article
- Export citation
Abstract almost periodicity for group actions on uniform topological spaces
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2023, pp. 798-829
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Correspondence theorems for Hopf algebroids with applications to affine groupoids
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2023, pp. 830-880
-
- Article
- Export citation
Positive Ulrich sheaves
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2023, pp. 881-914
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Logan’s problem for Jacobi transforms
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2023, pp. 915-945
-
- Article
- Export citation
Log p-divisible groups associated with log 1-motives
- Part of:
-
- Published online by Cambridge University Press:
- 28 April 2023, pp. 946-983
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A coloring invariant of 3-manifolds derived from their flow-spines and virtual knot diagrams
-
- Published online by Cambridge University Press:
- 02 May 2023, pp. 984-1004
-
- Article
- Export citation
On pointwise a.e. convergence of multilinear operators
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1005-1032
-
- Article
- Export citation
Torsion in the space of commuting elements in a Lie group
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1033-1061
-
- Article
- Export citation
Riesz-type criteria for L-functions in the Selberg class
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1062-1088
-
- Article
- Export citation
CJM volume 76 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 May 2024, pp. f1-f3
-
- Article
-
- You have access
- Export citation
CJM volume 76 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 May 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation