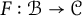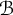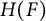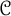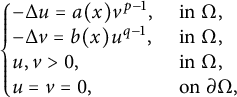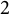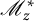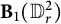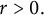FirstView articles
Article
The game of Cops and Robber on geodesic spaces
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fiber functors and reconstruction of Hopf algebras
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-44
-
- Article
-
- You have access
- HTML
- Export citation
Différentielles quadratiques à singularités prescrites
- Part of:
-
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-65
-
- Article
-
- You have access
- HTML
- Export citation
The Galvin property under the ultrapower axiom
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2024, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random walks and the “Euclidean” association scheme in finite vector spaces
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert direct integrals of monotone operators
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
Invariant scalar-flat Kähler metrics on line bundles over generalized flag varieties
- Part of:
-
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-26
-
- Article
-
- You have access
- HTML
- Export citation
A reproducing kernel approach to Lebesgue decomposition
- Part of:
-
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Heisenberg covering of the Fermat curve
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
Hyperbolic one-relator groups
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
Mirror symmetry and Hitchin system on Deligne–Mumford curves: Strominger–Yau–Zaslow duality
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-58
-
- Article
-
- You have access
- HTML
- Export citation
Higher Chow cycles on a family of Kummer surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-34
-
- Article
-
- You have access
- HTML
- Export citation
Random analytic functions with a prescribed growth rate in the unit disk
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence and symmetry breaking results for positive solutions of elliptic Hamiltonian systems
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2024, pp. 1-29
-
- Article
-
- You have access
- HTML
- Export citation
The Waring problem for upper triangular matrix algebras
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
Uniqueness and Hyers–Ulam’s stability for a fractional nonlinear partial integro-differential equation with variable coefficients and a mixed boundary condition
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirichlet-type spaces of the unit bidisc and toral 2-isometries
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isochronous centers and flat Finsler metrics (I)
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
Largest exact structures and almost split sequences on hearts of twin cotorsion pairs
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
Summation formulae of multiplicative functions over arithmetic progressions and applications
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-28
-
- Article
-
- You have access
- HTML
- Export citation