Hostname: page-component-5cf477f64f-xc2pj Total loading time: 0 Render date: 2025-04-06T04:14:50.914Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation and nonoscillation of a delay differential equation

Published online by Cambridge University Press:  17 April 2009

Chunhai Kou ,
Weiping Yan  and
Jurang Yan
Chunhai Kou
Affiliation:
Department of Information, Shanxi Economic Management Institute, Taiyuan, Shanxi 030006People's Republic of China Department of Mathematics, Shanxi University Taiyuan, Shanxi 030006, People's Republic of China
Weiping Yan
Affiliation:
Department of Mathematics, Shanxi University Taiyuan, Shanxi 030006, People's Republic of China
Jurang Yan
Affiliation:
Department of Mathematics, Shanxi University Taiyuan, Shanxi 030006, People's Republic of China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, some necessary and sufficient conditions for oscillation of a first order delay differential equation with oscillating coefficients of the form

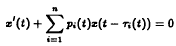
are established. Several applications of our results improve and generalise some of the known results in the literature.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 49 , Issue 1 , February 1994 , pp. 69 - 79
Copyright
Copyright © Australian Mathematical Society 1994

References

[1]Chen, Yongshao, ‘Oscillation and asymptotic behavior of solutions of first order linear functional differential equations with oscillatory coefficients’, (in Chinese), Acta Math. Appl. Sinica 12 (1989), 96–104.Google Scholar
[2]Györi, I. and Ladas, G., Oscillation theory of delay differential equations with applications (Clarendon Press, Oxford, 1991).CrossRefGoogle Scholar
[3]Hunt, B.R. and Yorke, J.A., ‘When all solutions of oscillate’, J. Differential Equations 53 (1984), 139–145.CrossRefGoogle Scholar
[4]Koplatadze, R.G. and Chanturia, T.A., ‘On the oscillatory and monotone solutions of first order differential equations with deviating arguments’, (in Russian), Differensial'nye Uravneniya 18 (1982), 1463–1465.Google Scholar
[5]Kulenovic, M.R. and Grammatikopoulos, M.K., ‘First order functional differential inequalities with oscillating coefficients’, Nonlinear Anal. 8 (1984), 1043–1054.CrossRefGoogle Scholar
[6]Kulenovic, M.R. and Grammatikopoulos, M.K., ‘Some comparison and oscillation results for first order differential equations and inequalities with a deviating argument’, J. Math. Anal. Appl. 131 (1988), 67–84.CrossRefGoogle Scholar
[7]Kwong, M.K., ‘Oscillation of first order delay equations’, J. Math. Anal. Appl. 156 (1991), 274–286.CrossRefGoogle Scholar
[8]Ladas, G., Sficas, Y.G. and Stavroulakis, I.P., ‘Functional differential inequalities and equations with oscillating coefficients’, in Trends in theory and practice of nonlinear differential equations, (Lakshmikantham, V., Editor) (Marcel Dekker, New York, Basel, 1984).Google Scholar
[9]Yu, J.S., Wang, Z.C., Zhang, B.C. and Qian, X.Z., ‘Oscillations of differential equations with deviating arguments’, Pan. Math. J. 2 (1992), 59–78.Google Scholar