Research Article
A remark on a third-order three-point boundary value problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-5
-
- Article
-
- You have access
- Export citation
Uniqueness of limit cycles in polynomial systems with algebraic invariants
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 7-20
-
- Article
-
- You have access
- Export citation
Two counter-examples in nonseparable Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 21-24
-
- Article
-
- You have access
- Export citation
Near-rings of homotopy classes of continuous functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 25-33
-
- Article
-
- You have access
- Export citation
On Morita duality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 35-46
-
- Article
-
- You have access
- Export citation
Maximal elements and equilibria for u-majorised preferences
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 47-54
-
- Article
-
- You have access
- Export citation
A note on prime essential rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 55-57
-
- Article
-
- You have access
- Export citation
When are dense subgroups of LCA groups closed under intersections?
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 59-67
-
- Article
-
- You have access
- Export citation
Oscillation and nonoscillation of a delay differential equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 69-79
-
- Article
-
- You have access
- Export citation
Primitive ideals of the quantised enveloping algebra of a complex lie algebra
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 81-84
-
- Article
-
- You have access
- Export citation
Skew fields with a non-trivial generalised power central rational identity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 85-90
-
- Article
-
- You have access
- Export citation
A note on fragmentable topological spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 91-100
-
- Article
-
- You have access
- Export citation
On the divergence of Hermite-Fejér type interpolation with equidistant nodes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 101-110
-
- Article
-
- You have access
- Export citation
A note on Fréchet and approximate subdifferentials of composite functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 111-115
-
- Article
-
- You have access
- Export citation
On distinguishing spaces not homotopy-equivalent
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 117-119
-
- Article
-
- You have access
- Export citation
On connected transversals to Abelian subgroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 121-128
-
- Article
-
- You have access
- Export citation
A chain rule for nonsmooth composite functions via minimisation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 129-137
-
- Article
-
- You have access
- Export citation
On generalised convex nonsmooth functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 139-149
-
- Article
-
- You have access
- Export citation
Symmetries of the self-dual Yang-Mills equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 151-158
-
- Article
-
- You have access
- Export citation
On weakly SI-modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 159-164
-
- Article
-
- You have access
- Export citation

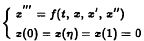
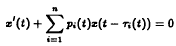
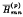 (
(