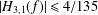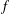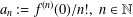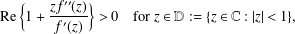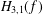Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 454
Weak and strong convergence to fixed points of asymptotically nonexpansive mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 153-159
-
- Article
-
- You have access
- Export citation
- Cited by 379
Fixed point theorems by altering distances between the points
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-9
-
- Article
-
- You have access
- Export citation
- Cited by 267
Invex functions and constrained local minima
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-366
-
- Article
-
- You have access
- Export citation
- Cited by 226
Another control condition in an iterative method for nonexpansive mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 109-113
-
- Article
-
- You have access
- Export citation
- Cited by 196
A family of Chebyshev-Halley type methods in Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 113-130
-
- Article
-
- You have access
- Export citation
- Cited by 190
Aspects of topoi
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-76
-
- Article
-
- You have access
- Export citation
- Cited by 161
On an elliptic equation of p-Kirchhoff type via variational methods
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 263-277
-
- Article
-
- You have access
- Export citation
- Cited by 148
Slant immersions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 135-147
-
- Article
-
- You have access
- Export citation
- Cited by 142
Near-rings in which each element is a power of itself
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 363-368
-
- Article
-
- You have access
- Export citation
- Cited by 138
On 2-absorbing ideals of commutative rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 417-429
-
- Article
-
- You have access
- Export citation
- Cited by 136
A fixed point theorem and its applications to a system of variational inequalities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-442
-
- Article
-
- You have access
- Export citation
- Cited by 132
Quadratic equations and applications to Chandrasekhar's and related equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 275-292
-
- Article
-
- You have access
- Export citation
- Cited by 124
A unified treatment of transfinite constructions for free algebras, free monoids, colimits, associated sheaves, and so on
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-83
-
- Article
-
- You have access
- Export citation
- Cited by 123
A new graph product and its spectrum
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 21-28
-
- Article
-
- You have access
- Export citation
- Cited by 116
Polyhedral decompositions of cubic graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 367-387
-
- Article
-
- You have access
- Export citation
- Cited by 115
A case of boundedness in Littlewood's problem on oscillatory differential equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 71-93
-
- Article
-
- You have access
- Export citation
- Cited by 109
Some notes on the method of moving planes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-434
-
- Article
-
- You have access
- Export citation
- Cited by 105
Matrix quadratic equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-401
-
- Article
-
- You have access
- Export citation
- Cited by 104
THE SHARP BOUND FOR THE HANKEL DETERMINANT OF THE THIRD KIND FOR CONVEX FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 04 April 2018, pp. 435-445
-
- Article
-
- You have access
- Export citation
- Cited by 102
A class of nonconvex functions and mathematical programming
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-189
-
- Article
-
- You have access
- Export citation

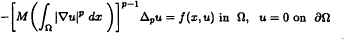 and
and
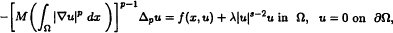 where Ω is a bounded smooth domain of ℝ
where Ω is a bounded smooth domain of ℝ = {
= {