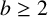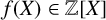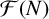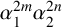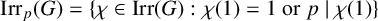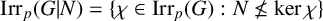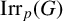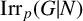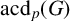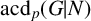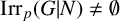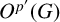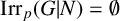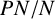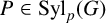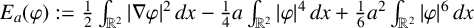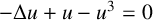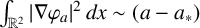Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
EVERY ARITHMETIC PROGRESSION CONTAINS INFINITELY MANY b-NIVEN NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 31 July 2023, pp. 409-413
-
- Article
- Export citation
ON THE DENSITY OF SUMSETS, II
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2023, pp. 414-419
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUMSETS CONTAINING A TERM OF A SEQUENCE
- Part of:
-
- Published online by Cambridge University Press:
- 18 September 2023, pp. 420-428
-
- Article
- Export citation
ADDITIVE COMPLETION OF THIN SETS
- Part of:
-
- Published online by Cambridge University Press:
- 15 November 2023, pp. 429-436
-
- Article
- Export citation
AN IMPROVEMENT TO A THEOREM OF LEONETTI AND LUCA
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2023, pp. 437-442
-
- Article
- Export citation
A NOTE ON THE GOORMAGHTIGH EQUATION CONCERNING DIFFERENCE SETS
- Part of:
-
- Published online by Cambridge University Press:
- 23 June 2023, pp. 443-452
-
- Article
- Export citation
LINEAR INDEPENDENCE OF VALUES OF THE q-EXPONENTIAL AND RELATED FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 23 October 2023, pp. 453-463
-
- Article
- Export citation
TRANSCENDENCE OF GENERALISED EULER–KRONECKER CONSTANTS
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2023, pp. 464-470
-
- Article
- Export citation
ON THE N-POINT CORRELATION OF VAN DER CORPUT SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2023, pp. 471-475
-
- Article
- Export citation
ON QUADRATIC FIELDS GENERATED BY POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2023, pp. 476-485
-
- Article
- Export citation
ON SUMS INVOLVING THE EULER TOTIENT FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 24 August 2023, pp. 486-497
-
- Article
- Export citation
AN ALGEBRAIC INTERPRETATION OF THE SUPER CATALAN NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2023, pp. 498-506
-
- Article
- Export citation
ON p-SOLVABILITY AND AVERAGE CHARACTER DEGREE IN A FINITE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 27 July 2023, pp. 507-511
-
- Article
- Export citation
LOCALLY FINITE SIMPLE GROUPS WHOSE NONNILPOTENT SUBGROUPS ARE PRONORMAL
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2023, pp. 512-521
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE GROUPS WITH HEREDITARILY G-PERMUTABLE SCHMIDT SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 28 July 2023, pp. 522-528
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH FEW NONPOWER SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 10 August 2023, pp. 529-540
-
- Article
- Export citation
ON SEPARATE CONTINUITY AND SEPARATE CONVEXITY: A SYNTHETIC TREATMENT FOR FUNCTIONS AND SETS
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2023, pp. 541-551
-
- Article
- Export citation
A NOTE ON NORMALISED GROUND STATES FOR THE TWO-DIMENSIONAL CUBIC-QUINTIC NONLINEAR SCHRÖDINGER EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2023, pp. 552-561
-
- Article
- Export citation
ON REAL NONISOMORPHIC BANACH SPACES WITH HOMEOMORPHIC GEOMETRIC STRUCTURE SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 26 July 2023, pp. 562-570
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CURVATURE-TORSION ENTROPY FOR TWISTED CURVES UNDER CURVE SHORTENING FLOW
- Part of:
-
- Published online by Cambridge University Press:
- 11 July 2023, pp. 571-580
-
- Article
-
- You have access
- Open access
- HTML
- Export citation