No CrossRef data available.
Article contents
ON THE N-POINT CORRELATION OF VAN DER CORPUT SEQUENCES
Part of:
Probabilistic theory: distribution modulo $1$; metric theory of algorithms
Multivariate analysis
Published online by Cambridge University Press: 15 September 2023
Abstract
We derive an explicit formula for the N-point correlation 
$F_N(s)$ of the van der Corput sequence in base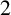 
$2$ for all 
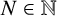$N \in \mathbb {N}$ and 
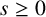$s \geq 0$. The formula can be evaluated without explicit knowledge about the elements of the van der Corput sequence. This constitutes the first example of an exact closed-form expression of 
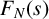$F_N(s)$ for all 
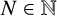$N \in \mathbb {N}$ and all 
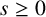$s \geq 0$ which does not require explicit knowledge about the involved sequence. Moreover, it can be immediately read off that 
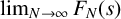$\lim _{N \to \infty } F_N(s)$ exists only for 
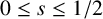$0 \leq s \leq 1/2$.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
Drmota, M. and Tichy, R., Sequences, Discrepancies and Applications, Lecture Notes in Mathematics, 1651 (Springer, Berlin, 1997).CrossRefGoogle Scholar
El-Baz, D., Marklof, J. and Vinogradov, I., ‘The two-point correlation function of the fractional parts of
$\sqrt{n}$
is Poisson’, Proc. Amer. Math. Soc. 143(7) (2015), 2815–2828.CrossRefGoogle Scholar
$\sqrt{n}$
is Poisson’, Proc. Amer. Math. Soc. 143(7) (2015), 2815–2828.CrossRefGoogle ScholarKuipers, L. and Niederreiter, H., Uniform Distribution of Sequences (Wiley, New York, 1974).Google Scholar
Lutsko, C., ‘Directions in orbits of geometrically finite hyperbolic subgroups’, Math. Proc. Cambridge Philos. Soc. 171(2) (2020), 277–316.CrossRefGoogle Scholar
Lutsko, C., Sourmelidis, A. and Technau, N., ‘Pair correlation of the fractional parts of
$\alpha {n}^{\theta }$
’, Preprint, 2023, arXiv:2106.09800.Google Scholar
$\alpha {n}^{\theta }$
’, Preprint, 2023, arXiv:2106.09800.Google ScholarLutsko, C. and Technau, N., ‘Correlations of the fractional parts of
$\alpha {n}^{\theta }$
’, Preprint, 2021, arXiv:2112.11524.Google Scholar
$\alpha {n}^{\theta }$
’, Preprint, 2021, arXiv:2112.11524.Google ScholarLutsko, C. and Technau, N., ‘Full Poissonian local statistics of slowly growing sequences’, Preprint, 2022, arXiv:2206.07809.Google Scholar
Marklof, J., ‘Distribution modulo one and Ratner’s theorem’, in: Equidistribution in Number Theory, An Introduction, NATO Science Series, 237 (eds. Granville, A. and Rudnick, Z.) (Springer, Dordrecht, 2007).Google Scholar
Marklof, J. and Strömbergsson, A., ‘Gaps between logs’, Bull. Lond. Math. Soc. 45(6) (2013), 1267–1280.CrossRefGoogle Scholar
Niederreiter, H., Random Number Generation and Quasi-Monte Carlo Methods, CBMS-NSF Series in Applied Mathematics, 63 (SIAM, Philadelphia, PA, 1992).CrossRefGoogle Scholar
Sayous, R., ‘Effective pair correlations of fractional powers of integers’, Preprint, 2023, arXiv:2306.00793.Google Scholar
Weiß, C., ‘Some connections between discrepancy, finite gap properties and pair correlations’, Monatsh. Math. 199 (2022), 909–927.CrossRefGoogle Scholar
Weiß, C., ‘An explicit non-Poissonian pair correlation function’, Preprint, 2023, arXiv:2304.14202.Google Scholar
Weiß, C. and Skill, T., ‘Sequences with almost Poissonian pair correlations’, J. Number Theory 236 (2022), 116–127.CrossRefGoogle Scholar