Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-01T06:46:26.540Z Has data issue: false hasContentIssue false
  • English
  • Français

ON QUADRATIC FIELDS GENERATED BY POLYNOMIALS

Part of: Algebraic number theory: global fields Multiplicative number theory Exponential sums and character sums

Published online by Cambridge University Press:  29 June 2023

IGOR E. SHPARLINSKI Open the ORCID record for IGOR E. SHPARLINSKI [Opens in a new window]
IGOR E. SHPARLINSKI*
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, NSW 2052, Australia
*
e-mail: igor.shparlinski@unsw.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 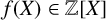$f(X) \in {\mathbb Z}[X]$ be a polynomial of degree 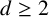$d \ge 2$ without multiple roots and let 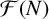${\mathcal F}(N)$ be the set of Farey fractions of order N. We use bounds for some new character sums and the square-sieve to obtain upper bounds, pointwise and on average, on the number of fields 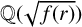${\mathbb Q}(\sqrt {f(r)})$ for 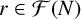$r\in {\mathcal F}(N)$ , with a given discriminant.

Keywords

quadratic fieldssquare sievecharacter sums

MSC classification

Primary: 11L40: Estimates on character sums
Secondary: 11N36: Applications of sieve methods 11R11: Quadratic extensions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

During the preparation of this work, the author was supported by the Australian Research Council Grant DP200100355.

References

Banks, W. D. and Shparlinski, I. E., ‘On coincidences among quadratic fields generated by the Shanks sequence’, Q. J. Math. 68 (2017), 465–484.Google Scholar
Bilu, Y., ‘Counting number fields in fibers (with an Appendix by Jean Gillibert)’, Math. Z. 288 (2018), 541–563.CrossRefGoogle Scholar
Bilu, Y. and Gillibert, J., ‘Chevalley–Weil theorem and subgroups of class groups’, Israel J. Math. 226 (2018), 927–956.CrossRefGoogle Scholar
Bilu, Y. and Luca, F., ‘Diversity in parametric families of number fields’, in: Number Theory—Diophantine Problems, Uniform Distribution and Applications (eds. Elsholtz, C. and Grabner, P.) (Springer, Cham, 2017), 169–191.CrossRefGoogle Scholar
Cutter, P., Granville, A. and Tucker, T. J., ‘The number of fields generated by the square root of values of a given polynomial’, Canad. Math. Bull. 46 (2003), 71–79.CrossRefGoogle Scholar
Dvornicich, R. and Zannier, U., ‘Fields containing values of algebraic functions’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 21 (1994), 421–443.Google Scholar
Heath-Brown, D. R., ‘The square sieve and consecutive square-free numbers’, Math. Ann. 266 (1984), 251–259.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘A mean value estimate for real character sums’, Acta Arith. 72 (1995), 235–275.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (American Mathematical Society, Providence, RI, 2004).Google Scholar
Kulkarni, K. and Levin, A., ‘Hilbert’s irreducibility theorem and ideal class groups of quadratic fields’, Acta Arith., to appear.Google Scholar
Luca, F. and Shparlinski, I. E., ‘Discriminants of complex multiplication fields of elliptic curves over finite fields’, Canad. Math. Bull. 50 (2007), 409–417.CrossRefGoogle Scholar
Luca, F. and Shparlinski, I. E., ‘Quadratic fields generated by polynomials’, Archiv Math. 91 (2008), 399–408.CrossRefGoogle Scholar
Patterson, R. D., van der Poorten, A. J. and Williams, H. C., ‘Characterization of a generalized Shanks sequence’, Pacific J. Math. 230 (2007), 185–215.CrossRefGoogle Scholar
Shanks, D., ‘On Gauss’s class number problems’, Math. Comp. 23 (1969), 151–163.Google Scholar
Stewart, C. L. and Top, J., ‘On ranks of twists of elliptic curves and power-free values of binary forms’, J. Amer. Math. Soc. 8 (1995), 943–973.CrossRefGoogle Scholar
van der Poorten, A. J. and Williams, H. C., ‘On certain continued fraction expansions of fixed period length’, Acta Arith. 89 (1999), 23–35.CrossRefGoogle Scholar
Williams, H. C., ‘Some generalizations of the ${S}_n$ sequence of Shanks’, Acta Arith. 69 (1995), 199–215.CrossRefGoogle Scholar