Hostname: page-component-848d4c4894-sjtt6 Total loading time: 0 Render date: 2024-06-29T03:36:55.718Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUPS WITH FEW NONPOWER SUBGROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  10 August 2023

JIWEI ZHENG Open the ORCID record for JIWEI ZHENG [Opens in a new window] ,
WEI ZHOU Open the ORCID record for WEI ZHOU [Opens in a new window]  and
D. E. TAYLOR Open the ORCID record for D. E. TAYLOR [Opens in a new window]
JIWEI ZHENG
Affiliation:
School of Mathematics and Statistics, Southwest University, Chonqing 400715, P.R. China e-mail: 1179157500@qq.com
WEI ZHOU*
Affiliation:
School of Mathematics and Statistics, Southwest University, Chonqing 400715, P.R. China
D. E. TAYLOR
Affiliation:
School of Mathematics and Statistics, The University of Sydney, New South Wales 2006, Australia e-mail: Donald.Taylor@sydney.edu.au
*
e-mail: zh_great@swu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

For a group G and 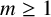$m\ge 1$, let 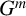$G^m$ denote the subgroup generated by the elements 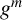$g^m$, where g runs through G. The subgroups not of the form 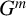$G^m$ are the nonpower subgroups of G. We classify the groups with at most nine nonpower subgroups.

Keywords

counting subgroupspower subgroupsnonpower subgroups

MSC classification

Primary: 20D25: Special subgroups (Frattini, Fitting, etc.)
Secondary: 20D60: Arithmetic and combinatorial problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 3 , June 2024 , pp. 529 - 540
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the National Natural Science Foundation of China (11971391, 12071376).

References

Anabanti, C. S., Aroh, A. B., Hart, S. B. and Oodo, A. R., ‘A question of Zhou, Shi and Duan on nonpower subgroups of finite groups’, Quaest. Math. 45(6) (2022), 901–910.CrossRefGoogle Scholar
Anabanti, C. S. and Hart, S. B., ‘Groups with a given number of nonpower subgroups’, Bull. Aust. Math. Soc. 106(2) (2022), 315–319.CrossRefGoogle Scholar
Berkovich, Y., ‘Short proofs of some basic characterization theorems of finite $p$ -group theory’, Glas. Mat. Ser. III 41(61) (2) (2006), 239–258.CrossRefGoogle Scholar
Blackburn, N., ‘On prime-power groups with two generators’, Proc. Cambridge Philos. Soc. 54 (1958), 327–337.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: The user language’, J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Gorenstein, D., Finite Groups, Harper’s Series in Mathematics (Harper and Row, New York–Evanston–London, 1968).Google Scholar
Szász, F., ‘On cyclic groups’, Fund. Math. 43 (1956), 238–240.CrossRefGoogle Scholar
Tǎrnǎuceanu, M., ‘An arithmetic method of counting the subgroups of a finite abelian group’, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 53(101) (4) (2010), 373–386.Google Scholar
Zhou, W., Shi, W. and Duan, Z., ‘A new criterion for finite noncyclic groups’, Comm. Algebra 34(12) (2006), 4453–4457.CrossRefGoogle Scholar