Let 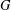$G$ be a finite group and 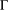${\rm\Gamma}$ a 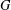$G$-symmetric graph. Suppose that 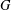$G$ is imprimitive on 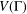$V({\rm\Gamma})$ with 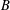$B$ a block of imprimitivity and 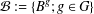${\mathcal{B}}:=\{B^{g};g\in G\}$ a system of imprimitivity of $G$ on 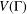$V({\rm\Gamma})$. Define 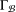${\rm\Gamma}_{{\mathcal{B}}}$ to be the graph with vertex set 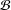${\mathcal{B}}$ such that two blocks 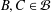$B,C\in {\mathcal{B}}$ are adjacent if and only if there exists at least one edge of 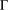${\rm\Gamma}$ joining a vertex in 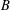$B$ and a vertex in 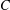$C$. Xu and Zhou [‘Symmetric graphs with 2-arc-transitive quotients’, J. Aust. Math. Soc. 96 (2014), 275–288] obtained necessary conditions under which the graph 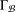${\rm\Gamma}_{{\mathcal{B}}}$ is 2-arc-transitive. In this paper, we completely settle one of the cases defined by certain parameters connected to 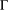${\rm\Gamma}$ and 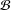${\mathcal{B}}$ and show that there is a unique graph corresponding to this case.