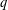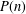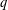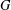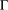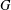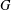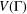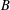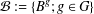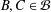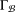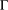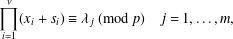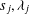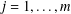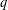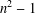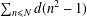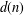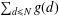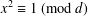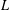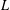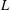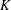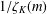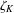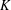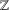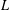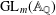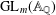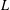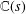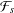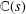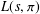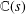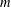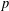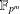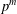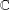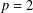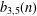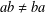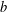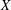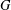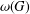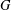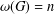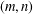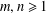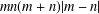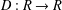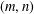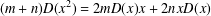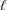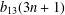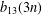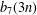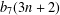Research Article
CAYLEY GRAPHS OVER A FINITE CHAIN RING AND GCD-GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 353-363
-
- Article
-
- You have access
- Export citation
STRONGLY
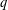 $q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
$q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
- Part of:
-
- Published online by Cambridge University Press:
- 17 November 2015, pp. 177-185
-
- Article
-
- You have access
- Export citation
UNIMODALITY AND COLOURED HOOK FACTORISATION
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 1-12
-
- Article
-
- You have access
- Export citation
ON MULTIPLE ZETA VALUES OF EXTREMAL HEIGHT
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 186-193
-
- Article
-
- You have access
- Export citation
FINITE SYMMETRIC GRAPHS WITH 2-ARC-TRANSITIVE QUOTIENTS: AFFINE CASE
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2015, pp. 13-18
-
- Article
-
- You have access
- Export citation
SYSTEMS OF CONGRUENCES WITH PRODUCTS OF VARIABLES FROM SHORT INTERVALS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 364-371
-
- Article
-
- You have access
- Export citation
A NOTE ON LACUNARY POWER SERIES WITH RATIONAL COEFFICIENTS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 372-374
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF DIVISORS OF
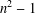 $n^{2}-1$
$n^{2}-1$
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2015, pp. 194-198
-
- Article
-
- You have access
- Export citation
A NOTE ON SIMPLE ZEROS OF PRIMITIVE DIRICHLET
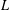 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 08 July 2015, pp. 19-30
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF INFINITE PRODUCTS OF CYCLOTOMIC POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2016, pp. 375-387
-
- Article
-
- You have access
- Export citation
ON THE MERTENS–CESÀRO THEOREM FOR NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 199-210
-
- Article
-
- You have access
- Export citation
A REMARK ON TAIL DISTRIBUTIONS OF PARTITION RANK AND CRANK
- Part of:
-
- Published online by Cambridge University Press:
- 20 August 2015, pp. 31-36
-
- Article
-
- You have access
- Export citation
THE SUBGROUP COMMUTATIVITY DEGREE OF FINITE
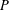 $P$-GROUPS
$P$-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 08 July 2015, pp. 37-41
-
- Article
-
- You have access
- Export citation
HYPERTRANSCENDENCE OF
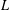 $L$-FUNCTIONS FOR
$L$-FUNCTIONS FOR 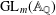 $\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
$\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 388-399
-
- Article
-
- You have access
- Export citation
MORE CONSTRUCTIONS OF APPROXIMATELY MUTUALLY UNBIASED BASES
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2015, pp. 211-222
-
- Article
-
- You have access
- Export citation
REFINED MOTIVIC DIMENSION OF SOME FERMAT VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 25 November 2015, pp. 223-230
-
- Article
-
- You have access
- Export citation
CONGRUENCES MODULO 2 FOR CERTAIN PARTITION FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 400-409
-
- Article
-
- You have access
- Export citation
ON NONCOMMUTING SETS AND CENTRALISERS IN INFINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 08 July 2015, pp. 42-46
-
- Article
-
- You have access
- Export citation
A NOTE ON
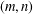 $(m,n)$-JORDAN DERIVATIONS OF RINGS AND BANACH ALGEBRAS
$(m,n)$-JORDAN DERIVATIONS OF RINGS AND BANACH ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2015, pp. 231-237
-
- Article
-
- You have access
- Export citation
THE 7-REGULAR AND 13-REGULAR PARTITION FUNCTIONS MODULO 3
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 410-419
-
- Article
-
- You have access
- Export citation