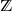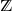1. Introduction and results
1.1. Self-interacting random walks
The study of self-interacting random walks began in 1983 in an article of Amit et al. [Reference Amit, Parisi and Peliti1]. Before [Reference Amit, Parisi and Peliti1], the expression ‘self-avoiding random walk’ referred to paths on graphs that do not intersect themselves. However, these are not easy to construct step by step; hence one would consider the set of all possible paths of a given length. Since one does not follow a single path as it grows with time, this is not really a random walk model. In order to work with an actual random walk model with self-avoiding behavior, the authors of [Reference Amit, Parisi and Peliti1] introduced the ‘true’ self-avoiding random walk. This is a random walk on
![]() $\mathbb{Z}^d$
for which, at each step, the position of the process at the next step is chosen randomly from among the neighbors of the current position, depending on the number of previous visits to said neighbors, with lower probabilities for those that have been visited the most. This process is a random walk in the sense that it is constructed step by step, but unlike most random walks in the literature, it is non-Markovian: at each step, the law of the next step depends on the whole past of the process.
$\mathbb{Z}^d$
for which, at each step, the position of the process at the next step is chosen randomly from among the neighbors of the current position, depending on the number of previous visits to said neighbors, with lower probabilities for those that have been visited the most. This process is a random walk in the sense that it is constructed step by step, but unlike most random walks in the literature, it is non-Markovian: at each step, the law of the next step depends on the whole past of the process.
It turns out that the ‘true’ self-avoiding random walk is hard to study. This led to the introduction by Tóth [Reference Tóth13, Reference Tóth14, Reference Tóth15] of non-Markovian random walks with bond repulsion, for which the probability of going from one site to another, instead of depending of the number of previous visits to the target, depends on the number of previous crossings of the undirected edge between the two sites, which is called the local time of the edge, with lower probabilities for the edges that have been crossed the most in the past. These walks are much easier to study, at least on
![]() $\unicode{x2124}$
, because one can apply the Ray–Knight approach to them. This approach was introduced by Ray and Knight in [Reference Ray11, Reference Knight2], and was used for the first time for non-Markovian random walks by Tóth in [Reference Tóth13, Reference Tóth14, Reference Tóth15]. Since then, it has been applied to many other non-Markovian random walks, such as a continuous-time version of the ‘true’ self-avoiding random walk in [Reference Tóth and Vető18], edge-reinforced random walks (see the corresponding part of the review [Reference Pemantle9] and references therein), and excited random walks (see [Reference Kosygina, Mountford and Peterson4] and references therein). The Ray–Knight approach works as follows: though the random walk itself is not Markovian, if we stop it when the local time at a given edge has reached a certain threshold, then the local times on the edges will form a Markov chain, which enables their analysis. Thanks to this approach, Tóth was able to prove scaling limits for the local times process for many different random walks with bond repulsion in his works [Reference Tóth13, Reference Tóth14, Reference Tóth15]. The law of the limit depends on the random walk model, but it is always a random process (the model studied by Tóth in [Reference Tóth16] has a deterministic limit, but it is not a random walk with bond repulsion, as it is self-attracting: the more an edge has been crossed in the past, the more likely it is to be crossed in the future).
$\unicode{x2124}$
, because one can apply the Ray–Knight approach to them. This approach was introduced by Ray and Knight in [Reference Ray11, Reference Knight2], and was used for the first time for non-Markovian random walks by Tóth in [Reference Tóth13, Reference Tóth14, Reference Tóth15]. Since then, it has been applied to many other non-Markovian random walks, such as a continuous-time version of the ‘true’ self-avoiding random walk in [Reference Tóth and Vető18], edge-reinforced random walks (see the corresponding part of the review [Reference Pemantle9] and references therein), and excited random walks (see [Reference Kosygina, Mountford and Peterson4] and references therein). The Ray–Knight approach works as follows: though the random walk itself is not Markovian, if we stop it when the local time at a given edge has reached a certain threshold, then the local times on the edges will form a Markov chain, which enables their analysis. Thanks to this approach, Tóth was able to prove scaling limits for the local times process for many different random walks with bond repulsion in his works [Reference Tóth13, Reference Tóth14, Reference Tóth15]. The law of the limit depends on the random walk model, but it is always a random process (the model studied by Tóth in [Reference Tóth16] has a deterministic limit, but it is not a random walk with bond repulsion, as it is self-attracting: the more an edge has been crossed in the past, the more likely it is to be crossed in the future).
1.2. The self-repelling random walk with directed edges
In 2008, Tóth and Vető [Reference Tóth and Vető17] introduced a process seemingly very similar to the aforementioned random walks with bond repulsion, in which the probability of going from one site to another depends on the number of crossings of the directed edge between them, instead of the crossings of the undirected edge. This process, called self-repelling random walk with directed edges, is a nearest-neighbor random walk on
![]() $\unicode{x2124}$
defined as follows. For any set A, we denote by
$\unicode{x2124}$
defined as follows. For any set A, we denote by
![]() $|A|$
the cardinality of A. Let
$|A|$
the cardinality of A. Let
![]() $w \,:\, \mathbb{Z} \mapsto (0,+\infty)$
be a non-decreasing and non-constant function. We will denote the walk by
$w \,:\, \mathbb{Z} \mapsto (0,+\infty)$
be a non-decreasing and non-constant function. We will denote the walk by
![]() $(X_n)_{n\in\mathbb{N}}$
. We set
$(X_n)_{n\in\mathbb{N}}$
. We set
![]() $X_0=0$
, and for any
$X_0=0$
, and for any
![]() $n\in\mathbb{N}$
,
$n\in\mathbb{N}$
,
![]() $i\in\mathbb{Z}$
, we denote by
$i\in\mathbb{Z}$
, we denote by
![]() $\ell^\pm(n,i)=|\{0 \leq m \leq n-1 \,|\, (X_m,X_{m+1})=(i,i\pm1)\}|$
the number of crossings of the directed edge
$\ell^\pm(n,i)=|\{0 \leq m \leq n-1 \,|\, (X_m,X_{m+1})=(i,i\pm1)\}|$
the number of crossings of the directed edge
![]() $(i,i\pm1)$
before time n, that is, the local time of the directed edge at time n. Then
$(i,i\pm1)$
before time n, that is, the local time of the directed edge at time n. Then
Using the local time of directed edges instead of that of undirected edges may seem like a very small change in the definition of the process, but the behavior of the self-repelling random walk with directed edges is actually very different from that of classical random walks with bond repulsion. Indeed, Tóth and Vető [Reference Tóth and Vető17] were able to prove that the local times process has a deterministic scaling limit, which is in sharp contrast with the random limit processes obtained for the random walks with bond repulsion on undirected edges [Reference Tóth13–Reference Tóth15] and even for the simple random walk [Reference Knight2].
The result of [Reference Tóth and Vető17] is as follows. For any
![]() $a\in\mathbb{R}$
, we let
$a\in\mathbb{R}$
, we let
![]() $a_+=\max(a,0)$
. If for any
$a_+=\max(a,0)$
. If for any
![]() $n\in\mathbb{N}$
,
$n\in\mathbb{N}$
,
![]() $i\in\mathbb{Z}$
, we denote by
$i\in\mathbb{Z}$
, we denote by
![]() $T_{n,i}^\pm$
the stopping time defined by
$T_{n,i}^\pm$
the stopping time defined by
![]() $T_{n,i}^\pm=\min\{m\in\mathbb{N}\,|\,\ell^\pm(m,i) = n\}$
, then
$T_{n,i}^\pm=\min\{m\in\mathbb{N}\,|\,\ell^\pm(m,i) = n\}$
, then
![]() $T_{n,i}^\pm$
is almost surely finite by Proposition 1 of [Reference Tóth and Vető17], and we have the following.
$T_{n,i}^\pm$
is almost surely finite by Proposition 1 of [Reference Tóth and Vető17], and we have the following.
Theorem 1. ([Reference Tóth and Vető17, Theorem 1].) For any
![]() $\theta>0$
,
$\theta>0$
,
![]() $x\in \mathbb{R}$
, we have that
$x\in \mathbb{R}$
, we have that
converges in probability to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
Thus the local times process of the self-repelling random walk with directed edges admits the deterministic scaling limit
![]() $y \mapsto \Big(\frac{|x|-|y|}{2}+\theta\Big)_+$
, which has the shape of a triangle. This also implies the following result on convergence to a deterministic limit for the
$y \mapsto \Big(\frac{|x|-|y|}{2}+\theta\Big)_+$
, which has the shape of a triangle. This also implies the following result on convergence to a deterministic limit for the
![]() $T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
.
$T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
.
Proposition 1. ([Reference Tóth and Vető17, Corollary 1].) For any
![]() $\theta>0$
,
$\theta>0$
,
![]() $x\in \mathbb{R}$
, we have that
$x\in \mathbb{R}$
, we have that
![]() $\frac{1}{N^2}T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
converges in probability to
$\frac{1}{N^2}T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
converges in probability to
![]() $(|x|+2\theta)^2$
when N tends to
$(|x|+2\theta)^2$
when N tends to
![]() $+\infty$
.
$+\infty$
.
The deterministic character of these limits makes the behavior of the self-repelling random walk with directed edges very unusual, hence worthy of study. In particular, it is natural to consider the possible fluctuations of the local times process and of the
![]() $T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
around their deterministic limits. However, before the present paper, nothing was known about these fluctuations. In this work, we prove convergence in distribution of the fluctuations of the local times process and of the
$T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
around their deterministic limits. However, before the present paper, nothing was known about these fluctuations. In this work, we prove convergence in distribution of the fluctuations of the local times process and of the
![]() $T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
. It happens that the limit of the fluctuations of the local times process is discontinuous; therefore, before stating the results, we have to be careful about the topology in which it may converge.
$T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
. It happens that the limit of the fluctuations of the local times process is discontinuous; therefore, before stating the results, we have to be careful about the topology in which it may converge.
1.3. Topologies for the convergence of the local times process
For any interval
![]() $I \subset R$
, let DI be the space of càdlàg functions on I, that is, the set of functions
$I \subset R$
, let DI be the space of càdlàg functions on I, that is, the set of functions
![]() $I \mapsto \mathbb{R}$
that are right-continuous and have left limits everywhere in I. For any function
$I \mapsto \mathbb{R}$
that are right-continuous and have left limits everywhere in I. For any function
![]() $Z \,:\, I \mapsto \mathbb{R}$
, we denote by
$Z \,:\, I \mapsto \mathbb{R}$
, we denote by
![]() $\|Z\|_\infty=\sup_{y\in I}|Z(y)|$
the uniform norm of Z on I. The uniform norm on I gives a topology on DI, but it is often too strong to deal with discontinuous functions.
$\|Z\|_\infty=\sup_{y\in I}|Z(y)|$
the uniform norm of Z on I. The uniform norm on I gives a topology on DI, but it is often too strong to deal with discontinuous functions.
For discontinuous càdlàg functions, the most widely used topology is the Skorokhod
![]() $J_1$
topology, introduced by Skorokhod in [Reference Skorokhod12] (see [Reference Pollard10, Chapter VI] for a course), which is often called ‘the’ Skorokhod topology. Intuitively, two functions are close in this topology if they are close for the uniform norm after allowing some small perturbation of time. Rigorously, for
$J_1$
topology, introduced by Skorokhod in [Reference Skorokhod12] (see [Reference Pollard10, Chapter VI] for a course), which is often called ‘the’ Skorokhod topology. Intuitively, two functions are close in this topology if they are close for the uniform norm after allowing some small perturbation of time. Rigorously, for
![]() $a<b$
in
$a<b$
in
![]() $\mathbb{R}$
, the Skorokhod
$\mathbb{R}$
, the Skorokhod
![]() $J_1$
topology on D[a, b] is defined as follows. We denote by
$J_1$
topology on D[a, b] is defined as follows. We denote by
![]() $\Lambda_{a,b}$
the set of functions
$\Lambda_{a,b}$
the set of functions
![]() $\lambda \,:\, [a,b] \mapsto [a,b]$
that are bijective, strictly increasing, and continuous (they correspond to the possible perturbations of time), and we denote by
$\lambda \,:\, [a,b] \mapsto [a,b]$
that are bijective, strictly increasing, and continuous (they correspond to the possible perturbations of time), and we denote by
![]() $\mathrm{Id}_{a,b} \,:\, [a,b] \mapsto [a,b]$
the identity map, defined by
$\mathrm{Id}_{a,b} \,:\, [a,b] \mapsto [a,b]$
the identity map, defined by
![]() $\mathrm{Id}_{a,b}(y)=y$
for all
$\mathrm{Id}_{a,b}(y)=y$
for all
![]() $y\in[a,b]$
. The Skorokhod
$y\in[a,b]$
. The Skorokhod
![]() $J_1$
topology on D[a, b] is defined through the following metric: for any
$J_1$
topology on D[a, b] is defined through the following metric: for any
![]() $Z_1,Z_2 \in D[a,b]$
, we set
$Z_1,Z_2 \in D[a,b]$
, we set
It can be proven rather easily that this is indeed a metric. We can then define the Skorokhod
![]() $J_1$
topology on
$J_1$
topology on
![]() $D({-}\infty,\infty)$
with the following metric: if for any sets
$D({-}\infty,\infty)$
with the following metric: if for any sets
![]() $A_1 \subset A_2$
and
$A_1 \subset A_2$
and
![]() $A_3$
and any function
$A_3$
and any function
![]() $Z\,:\,A_2 \mapsto A_3$
, we denote by
$Z\,:\,A_2 \mapsto A_3$
, we denote by
![]() $Z|_{A_1}$
the restriction of Z to
$Z|_{A_1}$
the restriction of Z to
![]() $A_1$
, then for
$A_1$
, then for
![]() $Z_1,Z_2 \in D({-}\infty,\infty)$
, we set
$Z_1,Z_2 \in D({-}\infty,\infty)$
, we set
The Skorokhod
![]() $J_1$
topology is widely used to study the convergence of càdlàg functions. However, when the limit function has a jump, which will be the case here, convergence in the Skorokhod
$J_1$
topology is widely used to study the convergence of càdlàg functions. However, when the limit function has a jump, which will be the case here, convergence in the Skorokhod
![]() $J_1$
topology requires the converging functions to have a single big jump approximating the jump of the limit process. To account for other cases, like having the jump of the limit functions approximated by several smaller jumps in quick succession or by a very steep continuous slope, one has to use a less restrictive topology, such as the Skorokhod
$J_1$
topology requires the converging functions to have a single big jump approximating the jump of the limit process. To account for other cases, like having the jump of the limit functions approximated by several smaller jumps in quick succession or by a very steep continuous slope, one has to use a less restrictive topology, such as the Skorokhod
![]() $M_1$
topology.
$M_1$
topology.
The Skorokhod
![]() $M_1$
topology was also introduced by Skorokhod in [Reference Skorokhod12] (see [Reference Whitt19, Section 3.3] for an overview). For any
$M_1$
topology was also introduced by Skorokhod in [Reference Skorokhod12] (see [Reference Whitt19, Section 3.3] for an overview). For any
![]() $a<b$
in
$a<b$
in
![]() $\mathbb{R}$
, the Skorokhod
$\mathbb{R}$
, the Skorokhod
![]() $M_1$
distance on D[a, b] is defined as follows: the distance between two functions will be roughly ‘the distance between the completed graphs of the functions’. More rigorously, if
$M_1$
distance on D[a, b] is defined as follows: the distance between two functions will be roughly ‘the distance between the completed graphs of the functions’. More rigorously, if
![]() $Z\in D[a,b]$
, we set
$Z\in D[a,b]$
, we set
![]() $Z(a^{-})=Z(a)$
, and for any
$Z(a^{-})=Z(a)$
, and for any
![]() $y \in (a,b]$
, we set
$y \in (a,b]$
, we set
![]() $Z(y^{-})=\lim_{y^{\prime} \to y, y^{\prime}<y}Z(y^{\prime})$
. Then the completed graph of Z is
$Z(y^{-})=\lim_{y^{\prime} \to y, y^{\prime}<y}Z(y^{\prime})$
. Then the completed graph of Z is
To express the ‘distance between two such completed graphs’, we need to define the parametric representations of
![]() $\Gamma_Z$
(by abuse of notation, we will often write ‘the parametric representations of Z’). We define an order on
$\Gamma_Z$
(by abuse of notation, we will often write ‘the parametric representations of Z’). We define an order on
![]() $\Gamma_Z$
as follows: for
$\Gamma_Z$
as follows: for
![]() $(y_1,z_1),(y_2,z_2) \in \Gamma_Z$
, we have
$(y_1,z_1),(y_2,z_2) \in \Gamma_Z$
, we have
![]() $(y_1,z_1) \leq (y_2,z_2)$
when
$(y_1,z_1) \leq (y_2,z_2)$
when
![]() $y_1 < y_2$
or when
$y_1 < y_2$
or when
![]() $y_1=y_2$
and
$y_1=y_2$
and
![]() $|Z\big(y_1^{-}\big)-z_1|\leq|Z\big(y_1^{-}\big)-z_2|$
. A parametric representation of
$|Z\big(y_1^{-}\big)-z_1|\leq|Z\big(y_1^{-}\big)-z_2|$
. A parametric representation of
![]() $\Gamma_Z$
is a continuous, surjective function
$\Gamma_Z$
is a continuous, surjective function
![]() $(u,r)\,:\,[0,1] \mapsto \Gamma_Z$
that is non-decreasing with respect to this order; thus intuitively, when t goes from 0 to 1, (u(t),r(t)) ‘travels through the completed graph of Z from its beginning to its end’. A parametric representation of Z always exists (see [Reference Whitt19, Remark 12.3.3]). For
$(u,r)\,:\,[0,1] \mapsto \Gamma_Z$
that is non-decreasing with respect to this order; thus intuitively, when t goes from 0 to 1, (u(t),r(t)) ‘travels through the completed graph of Z from its beginning to its end’. A parametric representation of Z always exists (see [Reference Whitt19, Remark 12.3.3]). For
![]() $Z_1,Z_2 \in D[a,b]$
, the Skorokhod
$Z_1,Z_2 \in D[a,b]$
, the Skorokhod
![]() $M_1$
distance between
$M_1$
distance between
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
, denoted by
$Z_2$
, denoted by
![]() $d_{M_1,a,b}(Z_1,Z_2)$
, is
$d_{M_1,a,b}(Z_1,Z_2)$
, is
![]() $\inf\big\{\max\big(\|u_1-u_2\|_\infty,\|r_1-r_2\|_\infty\big)\big\}$
, where the infimum is on the parametric representations
$\inf\big\{\max\big(\|u_1-u_2\|_\infty,\|r_1-r_2\|_\infty\big)\big\}$
, where the infimum is on the parametric representations
![]() $(u_1,r_1)$
of
$(u_1,r_1)$
of
![]() $Z_1$
and
$Z_1$
and
![]() $(u_2,r_2)$
of
$(u_2,r_2)$
of
![]() $Z_2$
. It can be proven that this indeed gives a metric (see [Reference Whitt19, Theorem 12.3.1]), and this metric defines the Skorokhod
$Z_2$
. It can be proven that this indeed gives a metric (see [Reference Whitt19, Theorem 12.3.1]), and this metric defines the Skorokhod
![]() $M_1$
topology on D[a, b]. For any
$M_1$
topology on D[a, b]. For any
![]() $a>0$
, we will denote
$a>0$
, we will denote
![]() $d_{M_1,-a,a}$
by
$d_{M_1,-a,a}$
by
![]() $d_{M_1,a}$
for short. We can now define the Skorokhod
$d_{M_1,a}$
for short. We can now define the Skorokhod
![]() $M_1$
topology in
$M_1$
topology in
![]() $D({-}\infty,\infty)$
through the following metric: for
$D({-}\infty,\infty)$
through the following metric: for
![]() $Z_1,Z_2 \in D({-}\infty,\infty)$
, we set
$Z_1,Z_2 \in D({-}\infty,\infty)$
, we set
It can be seen that the Skorokhod
![]() $M_1$
topology is weaker than the Skorokhod
$M_1$
topology is weaker than the Skorokhod
![]() $J_1$
topology (see [Reference Whitt19, Theorem 12.3.2]), and thus less restrictive. Indeed, since the distance between two functions is roughly ‘the distance between the completed graphs of the functions’, the Skorokhod
$J_1$
topology (see [Reference Whitt19, Theorem 12.3.2]), and thus less restrictive. Indeed, since the distance between two functions is roughly ‘the distance between the completed graphs of the functions’, the Skorokhod
![]() $M_1$
topology will allow a function with a jump to be the limit of functions with steep slopes or with several smaller jumps. For this reason, the Skorokhod
$M_1$
topology will allow a function with a jump to be the limit of functions with steep slopes or with several smaller jumps. For this reason, the Skorokhod
![]() $M_1$
topology is often more suitable when one is considering convergence to a discontinuous function.
$M_1$
topology is often more suitable when one is considering convergence to a discontinuous function.
1.4. Results
We are now ready to state our results on the convergence of the fluctuations of the local times process. For any
![]() $\theta>0$
,
$\theta>0$
,
![]() $x\in \mathbb{R}$
,
$x\in \mathbb{R}$
,
![]() $\iota\in\{+,-\}$
, for any
$\iota\in\{+,-\}$
, for any
![]() $N \in \mathbb{N}^*$
, we define functions
$N \in \mathbb{N}^*$
, we define functions
![]() $Y_N^{-},Y_N^+$
as follows: for any
$Y_N^{-},Y_N^+$
as follows: for any
![]() $y\in\mathbb{R}$
, we set
$y\in\mathbb{R}$
, we set
The functions
![]() $Y_N^\pm$
actually depend on
$Y_N^\pm$
actually depend on
![]() $\iota$
, but to make the notation lighter, we do not write this dependency explicitly. Moreover,
$\iota$
, but to make the notation lighter, we do not write this dependency explicitly. Moreover,
![]() $\big(B_y^x\big)_{y\in\mathbb{R}}$
will denote a two-sided Brownian motion with
$\big(B_y^x\big)_{y\in\mathbb{R}}$
will denote a two-sided Brownian motion with
![]() $B_x^x=0$
and variance
$B_x^x=0$
and variance
![]() $\mathrm{Var}(\rho_-)$
, where
$\mathrm{Var}(\rho_-)$
, where
![]() $\rho_-$
is the distribution on
$\rho_-$
is the distribution on
![]() $\unicode{x2124}$
defined later in (3). We prove the following convergence for the fluctuations of the local times process of the self-repelling random walk with directed edges.
$\unicode{x2124}$
defined later in (3). We prove the following convergence for the fluctuations of the local times process of the self-repelling random walk with directed edges.
Theorem 2.
For any
![]() $\theta>0$
,
$\theta>0$
,
![]() $x\in \mathbb{R}$
,
$x\in \mathbb{R}$
,
![]() $\iota\in\{+,-\}$
, the process
$\iota\in\{+,-\}$
, the process
![]() $Y_N^\pm$
converges in distribution to
$Y_N^\pm$
converges in distribution to
![]() $\Big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\Big)_{y\in\mathbb{R}}$
in the Skorokhod
$\Big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\Big)_{y\in\mathbb{R}}$
in the Skorokhod
![]() $M_1$
topology on
$M_1$
topology on
![]() $D({-}\infty,+\infty)$
when N tends to
$D({-}\infty,+\infty)$
when N tends to
![]() $+\infty$
.
$+\infty$
.
Therefore, the fluctuations of the local times process have a diffusive limit behavior. However, it is necessary to use the Skorokhod
![]() $M_1$
topology here, as the following result states that convergence does not occur in the stronger Skorokhod
$M_1$
topology here, as the following result states that convergence does not occur in the stronger Skorokhod
![]() $J_1$
topology.
$J_1$
topology.
Proposition 2.
For any
![]() $\theta>0$
,
$\theta>0$
,
![]() $x\in \mathbb{R}$
,
$x\in \mathbb{R}$
,
![]() $\iota\in\{+,-\}$
, the process
$\iota\in\{+,-\}$
, the process
![]() $Y_N^\pm$
does not converge in distribution in the Skorokhod
$Y_N^\pm$
does not converge in distribution in the Skorokhod
![]() $J_1$
topology on
$J_1$
topology on
![]() $D({-}\infty,+\infty)$
when N tends to
$D({-}\infty,+\infty)$
when N tends to
![]() $+\infty$
.
$+\infty$
.
We stress the fact that the use of the Skorokhod
![]() $M_1$
topology is required only to deal with the discontinuities of the limit process at
$M_1$
topology is required only to deal with the discontinuities of the limit process at
![]() $-|x|-2\theta$
and
$-|x|-2\theta$
and
![]() $|x|+2\theta$
. Indeed, if we consider the process on an interval that does not include
$|x|+2\theta$
. Indeed, if we consider the process on an interval that does not include
![]() $-|x|-2\theta$
or
$-|x|-2\theta$
or
![]() $|x|+2\theta$
, it converges in the much stronger topology given by the uniform norm, as stated in the following result.
$|x|+2\theta$
, it converges in the much stronger topology given by the uniform norm, as stated in the following result.
Proposition 3.
For any
![]() $\theta>0$
,
$\theta>0$
,
![]() $x\in \mathbb{R}$
,
$x\in \mathbb{R}$
,
![]() $\iota\in\{+,-\}$
, for any closed interval
$\iota\in\{+,-\}$
, for any closed interval
![]() $I\in\mathbb{R}$
that does not contain
$I\in\mathbb{R}$
that does not contain
![]() $-|x|-2\theta$
or
$-|x|-2\theta$
or
![]() $|x|+2\theta$
, the process
$|x|+2\theta$
, the process
![]() $\big(Y_N^\pm(y)\big)_{y\in I}$
converges in distribution to
$\big(Y_N^\pm(y)\big)_{y\in I}$
converges in distribution to
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in I}$
in the topology on DI given by the uniform norm when N tends to
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in I}$
in the topology on DI given by the uniform norm when N tends to
![]() $+\infty$
.
$+\infty$
.
Finally, we also prove the convergence of the fluctuations of
![]() $T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
. For any
$T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
. For any
![]() $\sigma^2>0$
, we denote by
$\sigma^2>0$
, we denote by
![]() $\mathcal{N}\big(0,\sigma^2\big)$
the Gaussian distribution with mean 0 and variance
$\mathcal{N}\big(0,\sigma^2\big)$
the Gaussian distribution with mean 0 and variance
![]() $\sigma^2$
, and we recall that
$\sigma^2$
, and we recall that
![]() $\rho_-$
will be defined in (3). We then have the following.
$\rho_-$
will be defined in (3). We then have the following.
Proposition 4.
For any
![]() $\theta>0$
,
$\theta>0$
,
![]() $x\in \mathbb{R}$
,
$x\in \mathbb{R}$
,
![]() $\iota\in\{+,-\}$
, we have that
$\iota\in\{+,-\}$
, we have that
converges in distribution to
![]() $\mathcal{N}(0,\frac{32}{3}\mathrm{Var}(\rho_-)((|x|+\theta)^3+\theta^3))$
when N tends to
$\mathcal{N}(0,\frac{32}{3}\mathrm{Var}(\rho_-)((|x|+\theta)^3+\theta^3))$
when N tends to
![]() $+\infty$
.
$+\infty$
.
Remark 1. Instead of studying the fluctuations of
![]() $\ell^\pm\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,.\Big)$
, it may seem more natural to consider those of
$\ell^\pm\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,.\Big)$
, it may seem more natural to consider those of
![]() $\ell^\pm(N^2,.)$
. However, the Ray–Knight arguments that allow one to study
$\ell^\pm(N^2,.)$
. However, the Ray–Knight arguments that allow one to study
![]() $\ell^\pm\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,.\Big)$
completely break down for
$\ell^\pm\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,.\Big)$
completely break down for
![]() $\ell^\pm(N^2,.)$
, and it is not even clear whether these two processes should have the same behavior.
$\ell^\pm(N^2,.)$
, and it is not even clear whether these two processes should have the same behavior.
Remark 2. Apart from the article of Tóth and Vető [Reference Tóth and Vető17] that introduced the self-repelling random walk with directed edges, there have been a few other works on this model. These works were motivated by another important question, that of the existence of a scaling limit for
![]() $(X_n)_{n \in \mathbb{N}}$
, which means the convergence in distribution of the process
$(X_n)_{n \in \mathbb{N}}$
, which means the convergence in distribution of the process
![]() $\big(\frac{1}{N^\alpha}X_{\lfloor Nt\rfloor}\big)_{t \geq 0}$
for some
$\big(\frac{1}{N^\alpha}X_{\lfloor Nt\rfloor}\big)_{t \geq 0}$
for some
![]() $\alpha$
. Obtaining such a scaling limit for the trajectory of the random walk is harder than obtaining scaling limits for the local times. Indeed, for the random walks with bond repulsion with undirected edges introduced by Tóth in [Reference Tóth13–Reference Tóth15], the scaling limits for the local times have been known since the introduction of the models, but the scaling limits for the trajectories are not known. Some results were proven by Kosygina, Mountford, and Peterson in [Reference Kosygina, Mountford and Peterson3], but they do not cover all models. For the self-repelling random walk with directed edges, the behavior of the scaling limit of the trajectory turns out to be surprising. Indeed, Mountford, Pimentel, and Valle proved in [Reference Mountford, Pimentel and Valle7] that
$\alpha$
. Obtaining such a scaling limit for the trajectory of the random walk is harder than obtaining scaling limits for the local times. Indeed, for the random walks with bond repulsion with undirected edges introduced by Tóth in [Reference Tóth13–Reference Tóth15], the scaling limits for the local times have been known since the introduction of the models, but the scaling limits for the trajectories are not known. Some results were proven by Kosygina, Mountford, and Peterson in [Reference Kosygina, Mountford and Peterson3], but they do not cover all models. For the self-repelling random walk with directed edges, the behavior of the scaling limit of the trajectory turns out to be surprising. Indeed, Mountford, Pimentel, and Valle proved in [Reference Mountford, Pimentel and Valle7] that
![]() $\frac{1}{\sqrt{N}}X_N$
converges in distribution, but Mountford and the author showed in [Reference Marêché and Mountford6] that
$\frac{1}{\sqrt{N}}X_N$
converges in distribution, but Mountford and the author showed in [Reference Marêché and Mountford6] that
![]() $\big(\frac{1}{\sqrt{N}}X_{\lfloor Nt \rfloor}\big)_{t \geq 0}$
does not converge in distribution, and that the trajectories of the walk satisfy a more complex limit theorem, of a new kind.
$\big(\frac{1}{\sqrt{N}}X_{\lfloor Nt \rfloor}\big)_{t \geq 0}$
does not converge in distribution, and that the trajectories of the walk satisfy a more complex limit theorem, of a new kind.
1.5. Proof ideas
We begin by explaining why the limit of the local times process
![]() $Y_N^\pm$
is the process
$Y_N^\pm$
is the process
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
, and we describe the ideas behind the proofs of Theorem 2 and Proposition 3. To show the convergence of the local times process, we use a Ray–Knight argument; that is, we notice that
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
, and we describe the ideas behind the proofs of Theorem 2 and Proposition 3. To show the convergence of the local times process, we use a Ray–Knight argument; that is, we notice that
![]() $\Big(\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)\Big)_i$
is a Markov chain. Moreover, as long as
$\Big(\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)\Big)_i$
is a Markov chain. Moreover, as long as
![]() $\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)$
is not too low, the quantities
$\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)$
is not too low, the quantities
will roughly be independent and identically distributed (i.i.d.) random variables, in the sense that they can be coupled with i.i.d. random variables with a high probability of being equal to them. This coupling was already used in [Reference Tóth and Vető17] to prove the convergence of
![]() $\frac{1}{N}\ell^+\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm,\lfloor N y\rfloor\Big)$
to its deterministic limit (for a given y, the coupling makes this convergence a law of large numbers). However, when
$\frac{1}{N}\ell^+\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm,\lfloor N y\rfloor\Big)$
to its deterministic limit (for a given y, the coupling makes this convergence a law of large numbers). However, when
![]() $\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor\Big)$
is too low, the coupling fails and the
$\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor\Big)$
is too low, the coupling fails and the
![]() $\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor+1\Big)-\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor\Big)$
are no longer i.i.d. We have to prove that this occurs only around
$\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor+1\Big)-\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor\Big)$
are no longer i.i.d. We have to prove that this occurs only around
![]() $|x|+2\theta$
and
$|x|+2\theta$
and
![]() $-|x|-2\theta$
, and most of our work is dealing with what happens there. To show that it occurs only around
$-|x|-2\theta$
, and most of our work is dealing with what happens there. To show that it occurs only around
![]() $|x|+2\theta$
and
$|x|+2\theta$
and
![]() $-|x|-2\theta$
, we control the amplitude of the fluctuations to prove that the local times are close to their deterministic limit. This limit is large inside
$-|x|-2\theta$
, we control the amplitude of the fluctuations to prove that the local times are close to their deterministic limit. This limit is large inside
![]() $({-}|x|-2\theta,|x|+2\theta)$
, so we can use the coupling inside this interval; thus the
$({-}|x|-2\theta,|x|+2\theta)$
, so we can use the coupling inside this interval; thus the
![]() $\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor+1\Big)-\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor\Big)$
are roughly i.i.d. there, and hence the fluctuations will converge to a Brownian motion by Donsker’s invariance principle. When we are close to
$\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor+1\Big)-\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor\Big)$
are roughly i.i.d. there, and hence the fluctuations will converge to a Brownian motion by Donsker’s invariance principle. When we are close to
![]() $|x|+2\theta$
(the same reasoning works for
$|x|+2\theta$
(the same reasoning works for
![]() $-|x|-2\theta$
), the deterministic limit will be small, and hence the local times will also be small; tools from [Reference Tóth and Vető17] then allow us to prove that they reach 0 quickly. Once they reach 0, we notice that for
$-|x|-2\theta$
), the deterministic limit will be small, and hence the local times will also be small; tools from [Reference Tóth and Vető17] then allow us to prove that they reach 0 quickly. Once they reach 0, we notice that for
![]() $y \geq |x|+2\theta$
, if
$y \geq |x|+2\theta$
, if
![]() $\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor\Big)=0$
, then the walk X did not go from
$\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor\Big)=0$
, then the walk X did not go from
![]() $\lfloor N y\rfloor$
to
$\lfloor N y\rfloor$
to
![]() $\lfloor N y\rfloor+1$
before time
$\lfloor N y\rfloor+1$
before time
![]() $T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota$
, so it did not go to
$T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota$
, so it did not go to
![]() $\lfloor N y\rfloor+1$
before time
$\lfloor N y\rfloor+1$
before time
![]() $T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota$
; hence
$T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota$
; hence
![]() $\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,j\Big)=0$
for any
$\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,j\Big)=0$
for any
![]() $j \geq \lfloor N y\rfloor$
. Therefore, once the local times process reaches 0, it stays there. Consequently, we expect
$j \geq \lfloor N y\rfloor$
. Therefore, once the local times process reaches 0, it stays there. Consequently, we expect
![]() $\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor\Big)$
to be 0 when
$\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,\lfloor N y\rfloor\Big)$
to be 0 when
![]() $y > |x|+2\theta$
, and thus to have no fluctuations when
$y > |x|+2\theta$
, and thus to have no fluctuations when
![]() $y > |x|+2\theta$
; similar statements hold when
$y > |x|+2\theta$
; similar statements hold when
![]() $y < -|x|-2\theta$
. This is why our limit is
$y < -|x|-2\theta$
. This is why our limit is
![]() $\Big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\Big)_{y\in\mathbb{R}}$
.
$\Big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\Big)_{y\in\mathbb{R}}$
.
Since Proposition 3 only describes convergence away from
![]() $-|x|-2\theta$
and
$-|x|-2\theta$
and
![]() $|x|+2\theta$
, the previous arguments are enough to prove it. To prove the convergence in the Skorokhod
$|x|+2\theta$
, the previous arguments are enough to prove it. To prove the convergence in the Skorokhod
![]() $M_1$
topology on
$M_1$
topology on
![]() $D({-}\infty,+\infty)$
stated in Theorem 2, we need to handle what happens around
$D({-}\infty,+\infty)$
stated in Theorem 2, we need to handle what happens around
![]() $-|x|-2\theta$
and
$-|x|-2\theta$
and
![]() $|x|+2\theta$
with more precision. We first have to bound the difference between the local times and the i.i.d. random variables of the coupling even where the coupling fails. Afterwards comes the most important part of the paper: defining parametric representations of
$|x|+2\theta$
with more precision. We first have to bound the difference between the local times and the i.i.d. random variables of the coupling even where the coupling fails. Afterwards comes the most important part of the paper: defining parametric representations of
![]() $Y_N^\pm$
and of the sum of the i.i.d. random variables of the coupling, properly renormalized and set to 0 outside of
$Y_N^\pm$
and of the sum of the i.i.d. random variables of the coupling, properly renormalized and set to 0 outside of
![]() $[{-}|x|-2\theta,|x|+2\theta)$
, and then proving that they are close to each other. That allows us to prove that
$[{-}|x|-2\theta,|x|+2\theta)$
, and then proving that they are close to each other. That allows us to prove that
![]() $Y_N^\pm$
is close in the Skorokhod
$Y_N^\pm$
is close in the Skorokhod
![]() $M_1$
distance to a process that will converge in distribution to
$M_1$
distance to a process that will converge in distribution to
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
in the Skorokhod
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
in the Skorokhod
![]() $M_1$
topology, which lets us complete the proof of Theorem 2.
$M_1$
topology, which lets us complete the proof of Theorem 2.
To prove Proposition 2, that is, that
![]() $Y_N^\pm$
does not converge in the
$Y_N^\pm$
does not converge in the
![]() $J_1$
topology, we first notice that since the
$J_1$
topology, we first notice that since the
![]() $J_1$
topology is stronger than the
$J_1$
topology is stronger than the
![]() $M_1$
topology, if
$M_1$
topology, if
![]() $Y_N^\pm$
did converge in the
$Y_N^\pm$
did converge in the
![]() $J_1$
topology its limit would be
$J_1$
topology its limit would be
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
. However, this is not possible, as
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
. However, this is not possible, as
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
has a jump at
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
has a jump at
![]() $|x|+2\theta$
, while the jumps of
$|x|+2\theta$
, while the jumps of
![]() $Y_N^\pm$
have typical size of order
$Y_N^\pm$
have typical size of order
![]() $\frac{1}{\sqrt{N}}$
, so the jump in
$\frac{1}{\sqrt{N}}$
, so the jump in
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
is approximated in
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
is approximated in
![]() $Y_N^\pm$
by either a sequence of small jumps or a continuous slope, which prevents the convergence in the Skorokhod
$Y_N^\pm$
by either a sequence of small jumps or a continuous slope, which prevents the convergence in the Skorokhod
![]() $J_1$
topology.
$J_1$
topology.
Finally, to prove Proposition 4 on the fluctuations of
![]() $T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota$
, we use the fact that we have
$T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota$
, we use the fact that we have
It can be checked that
![]() $\Big|\ell^+\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)-\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i+1\Big)\Big|$
equals 0 or 1; hence it is enough to control the
$\Big|\ell^+\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)-\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i+1\Big)\Big|$
equals 0 or 1; hence it is enough to control the
![]() $\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)$
. By using the coupling for the
$\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)$
. By using the coupling for the
when
![]() $\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)$
is high enough, and using our estimates on the size of the window in which
$\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)$
is high enough, and using our estimates on the size of the window in which
![]() $\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)$
is neither high enough nor 0, we can prove that
$\ell^{-}\Big(T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota,i\Big)$
is neither high enough nor 0, we can prove that
![]() $T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota$
is close to the integral of the sum of the i.i.d. random variables of the coupling, which will yield the convergence.
$T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota$
is close to the integral of the sum of the i.i.d. random variables of the coupling, which will yield the convergence.
1.6. Organization of the paper
In Section 2, we define the coupling between the increments of the local time and i.i.d. random variables and prove some of its properties. In Section 3, we control where the local times hit 0, as well as where the local times are too low for the coupling of Section 2 to be useful. In Section 4, we prove a bound on the Skorokhod
![]() $M_1$
distance between
$M_1$
distance between
![]() $Y_N^\pm$
and the renormalized sum of the i.i.d. random variables of the coupling set to 0 outside of
$Y_N^\pm$
and the renormalized sum of the i.i.d. random variables of the coupling set to 0 outside of
![]() $[{-}|x|-2\theta,|x|+2\theta)$
, by writing explicit parametric representations of the two functions. In Section 5, we complete the proof of the convergence of
$[{-}|x|-2\theta,|x|+2\theta)$
, by writing explicit parametric representations of the two functions. In Section 5, we complete the proof of the convergence of
![]() $Y_N^\pm$
stated in Theorem 2 and Proposition 3. In Section 6 we prove that, as claimed in Proposition 2,
$Y_N^\pm$
stated in Theorem 2 and Proposition 3. In Section 6 we prove that, as claimed in Proposition 2,
![]() $Y_N^\pm$
does not converge in the
$Y_N^\pm$
does not converge in the
![]() $J_1$
topology. Finally, in Section 7 we prove the convergence of the fluctuations of
$J_1$
topology. Finally, in Section 7 we prove the convergence of the fluctuations of
![]() $T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
stated in Proposition 4.
$T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\pm$
stated in Proposition 4.
In what follows, we set
![]() $\theta>0$
,
$\theta>0$
,
![]() $\iota\in\{+,-\}$
, and
$\iota\in\{+,-\}$
, and
![]() $x > 0$
(the cases
$x > 0$
(the cases
![]() $x<0$
and
$x<0$
and
![]() $x=0$
can be dealt with in the same way). To simplify the notation, we set
$x=0$
can be dealt with in the same way). To simplify the notation, we set
![]() $T_N=T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota$
. Moreover, for any
$T_N=T_{\lfloor N \theta\rfloor,\lfloor N x\rfloor}^\iota$
. Moreover, for any
![]() $a,b\in\mathbb{R}$
, we set
$a,b\in\mathbb{R}$
, we set
![]() $a \vee b=\max(a,b)$
and
$a \vee b=\max(a,b)$
and
![]() $a \wedge b=\min(a,b)$
.
$a \wedge b=\min(a,b)$
.
2. Coupling of the local times increments with i.i.d. random variables
Our goal in this section will be to couple the
![]() $\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
with i.i.d. random variables and to prove some properties of this coupling. This part of the work is not very different from what was done in [Reference Tóth and Vető17], but we still recall the concepts and definitions from that paper. If we fix
$\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
with i.i.d. random variables and to prove some properties of this coupling. This part of the work is not very different from what was done in [Reference Tóth and Vető17], but we still recall the concepts and definitions from that paper. If we fix
![]() $i\in\mathbb{Z}$
and observe the evolution of
$i\in\mathbb{Z}$
and observe the evolution of
![]() $(\ell^{-}(n,i)-\ell^+(n,i))_{n\in\mathbb{N}}$
, and if we ignore the steps at which
$(\ell^{-}(n,i)-\ell^+(n,i))_{n\in\mathbb{N}}$
, and if we ignore the steps at which
![]() $\ell^{-}(n,i)-\ell^+(n,i)$
does not move (i.e. those at which the random walk is not at i), then we obtain a Markov chain
$\ell^{-}(n,i)-\ell^+(n,i)$
does not move (i.e. those at which the random walk is not at i), then we obtain a Markov chain
![]() $\xi_i$
whose distribution
$\xi_i$
whose distribution
![]() $\xi$
has the following transition probabilities: for all
$\xi$
has the following transition probabilities: for all
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
and
![]() $\xi_i(0)=0$
. Now, we set
$\xi_i(0)=0$
. Now, we set
![]() $\tau_{i,\pm}(0)=0$
, and for any
$\tau_{i,\pm}(0)=0$
, and for any
![]() $n\in\mathbb{N}$
, we define
$n\in\mathbb{N}$
, we define
![]() $\tau_{i,\pm}(n+1)=\inf\{m>\tau_{i,\pm}(n)\,|\,\xi_i(m)=\xi_i(m-1)\pm1\}$
, so that
$\tau_{i,\pm}(n+1)=\inf\{m>\tau_{i,\pm}(n)\,|\,\xi_i(m)=\xi_i(m-1)\pm1\}$
, so that
![]() $\tau_{i,+}(n)$
is the time of the nth upward step of
$\tau_{i,+}(n)$
is the time of the nth upward step of
![]() $\xi_i$
and
$\xi_i$
and
![]() $\tau_{i,-}(n)$
is the time of the nth downward step of
$\tau_{i,-}(n)$
is the time of the nth downward step of
![]() $\xi_i$
. Then, since the distribution of
$\xi_i$
. Then, since the distribution of
![]() $\xi$
is symmetric, the processes
$\xi$
is symmetric, the processes
![]() $(\eta_{i,+}(n))_{n\in\mathbb{N}}=({-}\xi_{i}(\tau_{i,+}(n)))_{n\in\mathbb{N}}$
and
$(\eta_{i,+}(n))_{n\in\mathbb{N}}=({-}\xi_{i}(\tau_{i,+}(n)))_{n\in\mathbb{N}}$
and
![]() $(\eta_{i,-}(n))_{n\in\mathbb{N}}=(\xi_{i}(\tau_{i,-}(n)))_{n\in\mathbb{N}}$
have the same distribution, called
$(\eta_{i,-}(n))_{n\in\mathbb{N}}=(\xi_{i}(\tau_{i,-}(n)))_{n\in\mathbb{N}}$
have the same distribution, called
![]() $\eta$
, and it can be checked that
$\eta$
, and it can be checked that
![]() $\eta$
is a Markov chain.
$\eta$
is a Markov chain.
We are going to give an expression for
![]() $\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
depending on the
$\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
depending on the
![]() $\eta_{i,-}$
,
$\eta_{i,-}$
,
![]() $\eta_{i,+}$
. We assume N large enough (so that
$\eta_{i,+}$
. We assume N large enough (so that
![]() $\lfloor N x\rfloor-1>0$
). By definition of
$\lfloor N x\rfloor-1>0$
). By definition of
![]() $T_N$
we have
$T_N$
we have
![]() $X_{T_N}=\lfloor N x\rfloor\iota 1$
. If
$X_{T_N}=\lfloor N x\rfloor\iota 1$
. If
![]() $i \leq 0$
we thus have
$i \leq 0$
we thus have
![]() $X_{T_N}>i$
, which means the last step of the walk at i before
$X_{T_N}>i$
, which means the last step of the walk at i before
![]() $T_N$
was going to the right, so the last step of
$T_N$
was going to the right, so the last step of
![]() $\xi_i$
was a downward step, and by definition of
$\xi_i$
was a downward step, and by definition of
![]() $\ell^+(T_N,i)$
we have that
$\ell^+(T_N,i)$
we have that
![]() $\xi_i$
made
$\xi_i$
made
![]() $\ell^+(T_N,i)$
downward steps; hence
$\ell^+(T_N,i)$
downward steps; hence
which yields
![]() $\ell^{-}(T_N,i)-\ell^+(T_N,i)=\eta_{i,-}(\ell^+(T_N,i))$
. In addition,
$\ell^{-}(T_N,i)-\ell^+(T_N,i)=\eta_{i,-}(\ell^+(T_N,i))$
. In addition,
![]() $\ell^{-}(T_N,i)=\ell^+(T_N,i-1)$
; hence
$\ell^{-}(T_N,i)=\ell^+(T_N,i-1)$
; hence
If
![]() $0 < i < \lfloor N x\rfloor$
(for
$0 < i < \lfloor N x\rfloor$
(for
![]() $\iota=-$
) or
$\iota=-$
) or
![]() $0 < i \leq \lfloor N x\rfloor$
(for
$0 < i \leq \lfloor N x\rfloor$
(for
![]() $\iota=+$
), the last step of the walk at i was also going to the right, so we also have
$\iota=+$
), the last step of the walk at i was also going to the right, so we also have
![]() $\ell^{-}(T_N,i)-\ell^+(T_N,i)=\eta_{i,-}(\ell^+(T_N,i))$
. However,
$\ell^{-}(T_N,i)-\ell^+(T_N,i)=\eta_{i,-}(\ell^+(T_N,i))$
. However,
![]() $\ell^{-}(T_N,i)=\ell^+(T_N,i-1)-1$
, so
$\ell^{-}(T_N,i)=\ell^+(T_N,i-1)-1$
, so
![]() $\ell^+(T_N,i-1)=\ell^+(T_N,i)+\eta_{i,-}(\ell^+(T_N,i))+1$
. Finally, if
$\ell^+(T_N,i-1)=\ell^+(T_N,i)+\eta_{i,-}(\ell^+(T_N,i))+1$
. Finally, if
![]() $i \geq \lfloor N x\rfloor$
(for
$i \geq \lfloor N x\rfloor$
(for
![]() $\iota=-$
) or
$\iota=-$
) or
![]() $i > \lfloor N x\rfloor$
(for
$i > \lfloor N x\rfloor$
(for
![]() $\iota=+$
), then the last step of the walk at i was going to the left, so the last step of
$\iota=+$
), then the last step of the walk at i was going to the left, so the last step of
![]() $\xi_i$
was an upward step, and
$\xi_i$
was an upward step, and
![]() $\xi_i$
made
$\xi_i$
made
![]() $\ell^{-}(T_N,i)$
upward steps; therefore
$\ell^{-}(T_N,i)$
upward steps; therefore
which yields
![]() $\ell^{-}(T_N,i)-\ell^+(T_N,i)=-\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)$
. Moreover,
$\ell^{-}(T_N,i)-\ell^+(T_N,i)=-\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)$
. Moreover,
![]() $\ell^+(T_N,i)=\ell^{-}(T_N,i+1)$
, and hence
$\ell^+(T_N,i)=\ell^{-}(T_N,i+1)$
, and hence
![]() $\ell^{-}(T_N,i+1)=\ell^{-}(T_N,i)+\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)$
.
$\ell^{-}(T_N,i+1)=\ell^{-}(T_N,i)+\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)$
.
We are going to use these results to deduce an expression for the
![]() $\ell^\pm(T_N,i)$
which will be very useful throughout this work. Defining
$\ell^\pm(T_N,i)$
which will be very useful throughout this work. Defining
![]() $\chi(N)=\lfloor N x\rfloor$
if
$\chi(N)=\lfloor N x\rfloor$
if
![]() $\iota=-$
and
$\iota=-$
and
![]() $\chi(N)=\lfloor N x\rfloor+1$
if
$\chi(N)=\lfloor N x\rfloor+1$
if
![]() $\iota=+$
, for
$\iota=+$
, for
![]() $i \geq \chi(N)$
we have
$i \geq \chi(N)$
we have
 \begin{equation*}\ell^{-}(T_N,i)=\ell^{-}(T_N,\chi(N))+\sum_{j=\chi(N)}^{i-1}\eta_{j,+}(\ell^{-}(T_N,j)),\end{equation*}
\begin{equation*}\ell^{-}(T_N,i)=\ell^{-}(T_N,\chi(N))+\sum_{j=\chi(N)}^{i-1}\eta_{j,+}(\ell^{-}(T_N,j)),\end{equation*}
and for
![]() $i < \chi(N)$
we have
$i < \chi(N)$
we have
 \begin{equation*}\ell^+(T_N,i)=\ell^+(T_N,\chi(N)-1)+\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}(\ell^+(T_N,j))+\mathbb{1}_{\{j > 0\}}\big).\end{equation*}
\begin{equation*}\ell^+(T_N,i)=\ell^+(T_N,\chi(N)-1)+\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}(\ell^+(T_N,j))+\mathbb{1}_{\{j > 0\}}\big).\end{equation*}
Now, we remember that the definition of
![]() $T_N$
implies
$T_N$
implies
![]() $\ell^\iota(T_N,\lfloor N x\rfloor)=\lfloor N \theta\rfloor$
, so if
$\ell^\iota(T_N,\lfloor N x\rfloor)=\lfloor N \theta\rfloor$
, so if
![]() $\iota=-$
we have
$\iota=-$
we have
![]() $\ell^{-}(T_N,\chi(N))=\lfloor N \theta\rfloor$
and
$\ell^{-}(T_N,\chi(N))=\lfloor N \theta\rfloor$
and
![]() $\ell^+(T_N,\chi(N)-1)=\ell^{-}(T_N,\chi(N))=\lfloor N \theta\rfloor$
, while if
$\ell^+(T_N,\chi(N)-1)=\ell^{-}(T_N,\chi(N))=\lfloor N \theta\rfloor$
, while if
![]() $\iota=+$
we have
$\iota=+$
we have
![]() $\ell^+(T_N,\chi(N)-1)=\lfloor N \theta\rfloor$
and
$\ell^+(T_N,\chi(N)-1)=\lfloor N \theta\rfloor$
and
![]() $\ell^{-}(T_N,\chi(N))=\ell^+(T_N,\chi(N)-1)-1=\lfloor N \theta\rfloor-1$
. Consequently, we have the following:
$\ell^{-}(T_N,\chi(N))=\ell^+(T_N,\chi(N)-1)-1=\lfloor N \theta\rfloor-1$
. Consequently, we have the following:
 \begin{equation}\begin{split} \textrm{If }i \geq \chi(N),& \quad \ell^{-}(T_N,i)=\lfloor N \theta\rfloor-\mathbb{1}_{\{\iota=+\}}+\sum_{j=\chi(N)}^{i-1}\eta_{j,+}(\ell^{-}(T_N,j)). \\ \textrm{If }i < \chi(N),& \quad \ell^+(T_N,i)=\lfloor N \theta\rfloor+\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}(\ell^+(T_N,j))+\mathbb{1}_{\{j > 0\}}\big). \end{split}\end{equation}
\begin{equation}\begin{split} \textrm{If }i \geq \chi(N),& \quad \ell^{-}(T_N,i)=\lfloor N \theta\rfloor-\mathbb{1}_{\{\iota=+\}}+\sum_{j=\chi(N)}^{i-1}\eta_{j,+}(\ell^{-}(T_N,j)). \\ \textrm{If }i < \chi(N),& \quad \ell^+(T_N,i)=\lfloor N \theta\rfloor+\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}(\ell^+(T_N,j))+\mathbb{1}_{\{j > 0\}}\big). \end{split}\end{equation}
We will also need to remember the following:
To couple the
![]() $\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
with i.i.d. random variables, we need to understand the
$\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
with i.i.d. random variables, we need to understand the
![]() $\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)$
and the
$\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)$
and the
![]() $\eta_{i,-}(\ell^+(T_N,i))$
. The paper [Reference Tóth and Vető17] proved that the following measure
$\eta_{i,-}(\ell^+(T_N,i))$
. The paper [Reference Tóth and Vető17] proved that the following measure
![]() $\rho_-$
is the unique invariant probability distribution of the Markov chain
$\rho_-$
is the unique invariant probability distribution of the Markov chain
![]() $\eta$
:
$\eta$
:
 \begin{equation} \forall i \in \mathbb{Z}, \quad \rho_-(i)=\frac{1}{R} \prod_{j=1}^{\lfloor|2i+1|/2\rfloor}\frac{w({-}j)}{w(j)}\quad\textrm{with}\quad R=\sum_{i\in\mathbb{Z}}\prod_{j=1}^{\lfloor|2i+1|/2\rfloor}\frac{w({-}j)}{w(j)}.\end{equation}
\begin{equation} \forall i \in \mathbb{Z}, \quad \rho_-(i)=\frac{1}{R} \prod_{j=1}^{\lfloor|2i+1|/2\rfloor}\frac{w({-}j)}{w(j)}\quad\textrm{with}\quad R=\sum_{i\in\mathbb{Z}}\prod_{j=1}^{\lfloor|2i+1|/2\rfloor}\frac{w({-}j)}{w(j)}.\end{equation}
We also denote by
![]() $\rho_0$
the measure on
$\rho_0$
the measure on
![]() $\frac{1}{2}+\mathbb{Z}$
defined by
$\frac{1}{2}+\mathbb{Z}$
defined by
![]() $\rho_0(\cdot)=\rho_-\big(\cdot-\frac{1}{2}\big)$
.
$\rho_0(\cdot)=\rho_-\big(\cdot-\frac{1}{2}\big)$
.
We are now in position to construct the coupling of the
![]() $\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
with i.i.d. random variables
$\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
with i.i.d. random variables
![]() $(\zeta_i)_{i\in\mathbb{Z}}$
. The idea is that
$(\zeta_i)_{i\in\mathbb{Z}}$
. The idea is that
![]() $\eta$
can be expected to converge to its invariant distribution
$\eta$
can be expected to converge to its invariant distribution
![]() $\rho_-$
; hence when
$\rho_-$
; hence when
![]() $\ell^\pm(T_N,i)$
is large,
$\ell^\pm(T_N,i)$
is large,
![]() $\eta_{i,\mp}\big(\ell^\pm(T_N,i)\big)$
will be close to a random variable of law
$\eta_{i,\mp}\big(\ell^\pm(T_N,i)\big)$
will be close to a random variable of law
![]() $\rho_-$
. More rigorously, we begin by defining an i.i.d. sequence
$\rho_-$
. More rigorously, we begin by defining an i.i.d. sequence
![]() $(r_i)_{i\in\mathbb{Z}}$
of random variables of distribution
$(r_i)_{i\in\mathbb{Z}}$
of random variables of distribution
![]() $\rho_-$
so that if
$\rho_-$
so that if
![]() $i \geq \chi(N)$
, then
$i \geq \chi(N)$
, then
![]() $\mathbb{P}\big(r_i \neq \eta_{i,+}\big(\big\lfloor N^{1/6}\big\rfloor\big)\big)$
is minimal, and if
$\mathbb{P}\big(r_i \neq \eta_{i,+}\big(\big\lfloor N^{1/6}\big\rfloor\big)\big)$
is minimal, and if
![]() $i < \chi(N)$
, then
$i < \chi(N)$
, then
![]() $\mathbb{P}\big(r_i \neq \eta_{i,-}\big(\big\lfloor N^{1/6}\big\rfloor\big)\big)$
is minimal. We can then define i.i.d. Markov chains
$\mathbb{P}\big(r_i \neq \eta_{i,-}\big(\big\lfloor N^{1/6}\big\rfloor\big)\big)$
is minimal. We can then define i.i.d. Markov chains
![]() $(\bar\eta_{i,+}(n))_{n \geq \big\lfloor N^{1/6}\big\rfloor}$
for
$(\bar\eta_{i,+}(n))_{n \geq \big\lfloor N^{1/6}\big\rfloor}$
for
![]() $i \geq \chi(N)$
and
$i \geq \chi(N)$
and
![]() $(\bar\eta_{i,-}(n))_{n \geq \big\lfloor N^{1/6}\big\rfloor}$
for
$(\bar\eta_{i,-}(n))_{n \geq \big\lfloor N^{1/6}\big\rfloor}$
for
![]() $i < \chi(N)$
so that
$i < \chi(N)$
so that
![]() $\bar\eta_{i,\pm}\big(\big\lfloor N^{1/6}\big\rfloor\big)=r_i$
,
$\bar\eta_{i,\pm}\big(\big\lfloor N^{1/6}\big\rfloor\big)=r_i$
,
![]() $\bar\eta_{i,\pm}$
is a Markov chain of distribution equal to that of
$\bar\eta_{i,\pm}$
is a Markov chain of distribution equal to that of
![]() $\eta$
, and if
$\eta$
, and if
![]() $\bar\eta_{i,\pm}\big(\big\lfloor N^{1/6}\big\rfloor\big)=\eta_{i,\pm}\big(\big\lfloor N^{1/6}\big\rfloor\big)$
, then
$\bar\eta_{i,\pm}\big(\big\lfloor N^{1/6}\big\rfloor\big)=\eta_{i,\pm}\big(\big\lfloor N^{1/6}\big\rfloor\big)$
, then
![]() $\bar\eta_{i,\pm}(n)=\eta_{i,\pm}(n)$
for any
$\bar\eta_{i,\pm}(n)=\eta_{i,\pm}(n)$
for any
![]() $n \geq \big\lfloor N^{1/6}\big\rfloor$
. Since
$n \geq \big\lfloor N^{1/6}\big\rfloor$
. Since
![]() $\rho_-$
is invariant for
$\rho_-$
is invariant for
![]() $\eta$
, if
$\eta$
, if
![]() $n \geq \big\lfloor N^{1/6}\big\rfloor$
, then the
$n \geq \big\lfloor N^{1/6}\big\rfloor$
, then the
![]() $\bar\eta_{i,+}(n)$
for
$\bar\eta_{i,+}(n)$
for
![]() $i \geq \chi(N)$
and
$i \geq \chi(N)$
and
![]() $\bar\eta_{i,-}(n)$
for
$\bar\eta_{i,-}(n)$
for
![]() $i < \chi(N)$
have distribution
$i < \chi(N)$
have distribution
![]() $\rho_-$
. We define the random variables
$\rho_-$
. We define the random variables
![]() $(\zeta_i)_{i\in\mathbb{Z}}$
as follows: for
$(\zeta_i)_{i\in\mathbb{Z}}$
as follows: for
![]() $i \geq \chi(N)$
we set
$i \geq \chi(N)$
we set
![]() $\zeta_i=\bar\eta_{i,+}\big(\ell^{-}(T_N,i)\vee\big\lfloor N^{1/6}\big\rfloor\big)+\frac{1}{2}$
, and for
$\zeta_i=\bar\eta_{i,+}\big(\ell^{-}(T_N,i)\vee\big\lfloor N^{1/6}\big\rfloor\big)+\frac{1}{2}$
, and for
![]() $i < \chi(N)$
we set
$i < \chi(N)$
we set
![]() $\zeta_i=\bar\eta_{i,-}\big(\ell^+(T_N,i)\vee\big\lfloor N^{1/6}\big\rfloor\big)+\frac{1}{2}$
. For
$\zeta_i=\bar\eta_{i,-}\big(\ell^+(T_N,i)\vee\big\lfloor N^{1/6}\big\rfloor\big)+\frac{1}{2}$
. For
![]() $i \geq \chi(N)$
, (1) implies that
$i \geq \chi(N)$
, (1) implies that
![]() $\ell^{-}(T_N,i)$
depends only on the
$\ell^{-}(T_N,i)$
depends only on the
![]() $\eta_{j,+}$
,
$\eta_{j,+}$
,
![]() $\chi(N) \leq j \leq i-1$
, and hence is independent from
$\chi(N) \leq j \leq i-1$
, and hence is independent from
![]() $\bar\eta_{i,+}$
, which implies that
$\bar\eta_{i,+}$
, which implies that
![]() $\zeta_i$
has distribution
$\zeta_i$
has distribution
![]() $\rho_0$
and is independent from the
$\rho_0$
and is independent from the
![]() $\zeta_j$
,
$\zeta_j$
,
![]() $\chi(N) \leq j \leq i-1$
. This together with a similar argument for
$\chi(N) \leq j \leq i-1$
. This together with a similar argument for
![]() $i < \chi(N)$
implies that the
$i < \chi(N)$
implies that the
![]() $(\zeta_i)_{i\in\mathbb{Z}}$
are i.i.d. with distribution
$(\zeta_i)_{i\in\mathbb{Z}}$
are i.i.d. with distribution
![]() $\rho_0$
.
$\rho_0$
.
We will prove several properties of
![]() $(\zeta_i)_{i\in\mathbb{Z}}$
that we will use in the remainder of the proof. In order to do that, we need the following lemma from [Reference Tóth and Vető17].
$(\zeta_i)_{i\in\mathbb{Z}}$
that we will use in the remainder of the proof. In order to do that, we need the following lemma from [Reference Tóth and Vető17].
Lemma 1. ([Reference Tóth and Vető17, Lemma 1].) There exist two constants
![]() $\tilde c =\tilde c(w)>0$
and
$\tilde c =\tilde c(w)>0$
and
![]() $\tilde C = \tilde C(w) < +\infty$
such that for any
$\tilde C = \tilde C(w) < +\infty$
such that for any
![]() $n\in\mathbb{N}$
,
$n\in\mathbb{N}$
,
Firstly, we want to prove that our coupling is actually useful: that the
![]() $\zeta_i$
are close to the
$\zeta_i$
are close to the
![]() $\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
. More precisely, we will show that except on an event of probability tending to 0, if
$\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
. More precisely, we will show that except on an event of probability tending to 0, if
![]() $\ell^\pm(T_N,i)$
is large then
$\ell^\pm(T_N,i)$
is large then
![]() $\zeta_i=\eta_{i,\mp}(\ell^\pm(T_N,i))+1/2$
, which (1) relates to
$\zeta_i=\eta_{i,\mp}(\ell^\pm(T_N,i))+1/2$
, which (1) relates to
![]() $\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
. We define
$\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
. We define
 \begin{equation}\begin{split} \mathcal{B}_1^{-}=\{\exists\, i\in\{-\lceil2(|x|+2\theta)N\rceil,\ldots,\chi(N)-1\}, \ell^+(T_N,i)\geq\big\lfloor N^{1/6}\big\rfloor\\ \textrm{ and }\zeta_i\neq\eta_{i,-}(\ell^+(T_N,i))+1/2\}, \\ \mathcal{B}_1^+=\{\exists\, i\in\{\chi(N),\ldots,\lceil2(|x|+2\theta)N\rceil\}, \ell^{-}(T_N,i)\geq\big\lfloor N^{1/6}\big\rfloor \qquad\;\,\\ \textrm{ and }\zeta_i\neq\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)+1/2\}. \end{split}\end{equation}
\begin{equation}\begin{split} \mathcal{B}_1^{-}=\{\exists\, i\in\{-\lceil2(|x|+2\theta)N\rceil,\ldots,\chi(N)-1\}, \ell^+(T_N,i)\geq\big\lfloor N^{1/6}\big\rfloor\\ \textrm{ and }\zeta_i\neq\eta_{i,-}(\ell^+(T_N,i))+1/2\}, \\ \mathcal{B}_1^+=\{\exists\, i\in\{\chi(N),\ldots,\lceil2(|x|+2\theta)N\rceil\}, \ell^{-}(T_N,i)\geq\big\lfloor N^{1/6}\big\rfloor \qquad\;\,\\ \textrm{ and }\zeta_i\neq\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)+1/2\}. \end{split}\end{equation}
Lemma 1 will allow us to prove the following.
Lemma 2.
![]() $\mathbb{P}\big(\mathcal{B}_1^{-}\big)$
and
$\mathbb{P}\big(\mathcal{B}_1^{-}\big)$
and
![]() $\mathbb{P}\big(\mathcal{B}_1^+\big)$
tend to 0 when
$\mathbb{P}\big(\mathcal{B}_1^+\big)$
tend to 0 when
![]() $N \to +\infty$
.
$N \to +\infty$
.
Proof. By definition, for any
![]() $i\in\{-\lceil2(|x|+2\theta)N\rceil,\ldots,\chi(N)-1\}$
we have
$i\in\{-\lceil2(|x|+2\theta)N\rceil,\ldots,\chi(N)-1\}$
we have
which is
![]() $\bar\eta_{i,-}(\ell^+(T_N,i))+\frac{1}{2}$
when
$\bar\eta_{i,-}(\ell^+(T_N,i))+\frac{1}{2}$
when
![]() $\ell^+(T_N,i)\geq\big\lfloor N^{1/6}\big\rfloor$
. Now,
$\ell^+(T_N,i)\geq\big\lfloor N^{1/6}\big\rfloor$
. Now,
![]() $\bar\eta_{i,-}=\eta_{i,-}$
if
$\bar\eta_{i,-}=\eta_{i,-}$
if
![]() $\bar\eta_{i,-}\big(\big\lfloor N^{1/6}\big\rfloor\big)=\eta_{i,-}\big(\big\lfloor N^{1/6}\big\rfloor\big)$
; that is,
$\bar\eta_{i,-}\big(\big\lfloor N^{1/6}\big\rfloor\big)=\eta_{i,-}\big(\big\lfloor N^{1/6}\big\rfloor\big)$
; that is,
![]() $r_i=\eta_{i,-}\big(\big\lfloor N^{1/6}\big\rfloor\big)$
. We deduce that
$r_i=\eta_{i,-}\big(\big\lfloor N^{1/6}\big\rfloor\big)$
. We deduce that
Now, for any
![]() $i < \chi(N)$
, we have
$i < \chi(N)$
, we have
![]() $\mathbb{P}\big(r_i\neq\eta_{i,-}\big(\big\lfloor N^{1/6}\big\rfloor\big)\big)$
minimal, and thus smaller than
$\mathbb{P}\big(r_i\neq\eta_{i,-}\big(\big\lfloor N^{1/6}\big\rfloor\big)\big)$
minimal, and thus smaller than
![]() $\tilde C e^{-\tilde c \big\lfloor N^{1/6}\big\rfloor}$
by Lemma 1. Consequently, when N is large enough, we have
$\tilde C e^{-\tilde c \big\lfloor N^{1/6}\big\rfloor}$
by Lemma 1. Consequently, when N is large enough, we have
![]() $\mathbb{P}\big(\mathcal{B}_1^{-}\big) \leq 3(|x|+2\theta)N\tilde C e^{-\tilde c \big\lfloor N^{1/6}\big\rfloor}$
, which tends to 0 when
$\mathbb{P}\big(\mathcal{B}_1^{-}\big) \leq 3(|x|+2\theta)N\tilde C e^{-\tilde c \big\lfloor N^{1/6}\big\rfloor}$
, which tends to 0 when
![]() $N \to +\infty$
. The proof for
$N \to +\infty$
. The proof for
![]() $\mathbb{P}\big(\mathcal{B}_1^+\big)$
is the same.
$\mathbb{P}\big(\mathcal{B}_1^+\big)$
is the same.
Unfortunately, the previous lemma does not allow us to control the local times when
![]() $\ell^\pm(T_N,i)$
is small. In order to do that, we show several additional properties. We have to control the probability of
$\ell^\pm(T_N,i)$
is small. In order to do that, we show several additional properties. We have to control the probability of
 \begin{equation*}\begin{split} \mathcal{B}_2=&\big\{\exists \, i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\lceil2(|x|+2\theta)N\rceil\}, |\zeta_i| \geq N^{1/16}\big\} \\ &\cup \big\{\exists \, i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\chi(N)-1\}, |\eta_{i,-}(\ell^+(T_N,i))+1/2| \geq N^{1/16}\big\} \\ &\cup \big\{\exists \, i \in \{\chi(N),\ldots,\lceil2(|x|+2\theta)N\rceil\}, |\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)+1/2| \geq N^{1/16}\big\}. \end{split}\end{equation*}
\begin{equation*}\begin{split} \mathcal{B}_2=&\big\{\exists \, i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\lceil2(|x|+2\theta)N\rceil\}, |\zeta_i| \geq N^{1/16}\big\} \\ &\cup \big\{\exists \, i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\chi(N)-1\}, |\eta_{i,-}(\ell^+(T_N,i))+1/2| \geq N^{1/16}\big\} \\ &\cup \big\{\exists \, i \in \{\chi(N),\ldots,\lceil2(|x|+2\theta)N\rceil\}, |\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)+1/2| \geq N^{1/16}\big\}. \end{split}\end{equation*}
Lemma 3.
![]() $\mathbb{P}(\mathcal{B}_2)$
tends to 0 when N tends to
$\mathbb{P}(\mathcal{B}_2)$
tends to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
Proof. It is enough to find some constants
![]() $c>0$
and
$c>0$
and
![]() $C < +\infty$
such that for any
$C < +\infty$
such that for any
![]() $i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\lceil2(|x|+2\theta)N\rceil\}$
we have
$i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\lceil2(|x|+2\theta)N\rceil\}$
we have
for any
![]() $i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\chi(N)-1\}$
we have
$i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\chi(N)-1\}$
we have
and for all
![]() $i \in \{\chi(N),\ldots,\lceil2(|x|+2\theta)N\rceil\}$
we have
$i \in \{\chi(N),\ldots,\lceil2(|x|+2\theta)N\rceil\}$
we have
For all
![]() $i\in\mathbb{Z}$
,
$i\in\mathbb{Z}$
,
![]() $\zeta_i$
has distribution
$\zeta_i$
has distribution
![]() $\rho_0$
, which has exponential tails; hence there exist constants
$\rho_0$
, which has exponential tails; hence there exist constants
![]() $c^{\prime}=c^{\prime}(w)>0$
and
$c^{\prime}=c^{\prime}(w)>0$
and
![]() $C^{\prime}=C^{\prime}(w) < +\infty$
such that for
$C^{\prime}=C^{\prime}(w) < +\infty$
such that for
![]() $i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\lceil2(|x|+2\theta)N\rceil\}$
we have
$i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\lceil2(|x|+2\theta)N\rceil\}$
we have
![]() $\mathbb{P}\big(|\zeta_i| \geq N^{1/16}\big) \leq C^{\prime}e^{-c^{\prime}N^{1/16}}$
. We now consider
$\mathbb{P}\big(|\zeta_i| \geq N^{1/16}\big) \leq C^{\prime}e^{-c^{\prime}N^{1/16}}$
. We now consider
![]() $i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\chi(N)-1\}$
and
$i \in \{-\lceil2(|x|+2\theta)N\rceil,\ldots,\chi(N)-1\}$
and
![]() $\mathbb{P}\big(|\eta_{i,-}(\ell^+(T_N,i))+1/2| \geq N^{1/16}\big)$
(the
$\mathbb{P}\big(|\eta_{i,-}(\ell^+(T_N,i))+1/2| \geq N^{1/16}\big)$
(the
![]() $\mathbb{P}\big(|\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)+1/2| \geq N^{1/16}\big)$
can be dealt with in the same way). Equation (1) implies that
$\mathbb{P}\big(|\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)+1/2| \geq N^{1/16}\big)$
can be dealt with in the same way). Equation (1) implies that
![]() $\ell^+(T_N,i)$
depends only on the
$\ell^+(T_N,i)$
depends only on the
![]() $\eta_{j,-}$
for
$\eta_{j,-}$
for
![]() $j>i$
, and hence is independent of
$j>i$
, and hence is independent of
![]() $\eta_{i,-}$
. This implies that
$\eta_{i,-}$
. This implies that
Therefore the first part of Lemma 1 implies that
 \begin{align*}\mathbb{P}\big(|\eta_{i,-}(\ell^+(T_N,i))+1/2| \geq N^{1/16}\big) &\leq \sum_{k\in\mathbb{N}}\frac{2\tilde C e^{\tilde c /2}}{1-e^{-\tilde c}}e^{-\tilde c N^{1/16}}\mathbb{P}\big(\ell^+(T_N,i)=k\big)\\&=\frac{2\tilde C e^{\tilde c /2}}{1-e^{-\tilde c}}e^{-\tilde c N^{1/16}},\end{align*}
\begin{align*}\mathbb{P}\big(|\eta_{i,-}(\ell^+(T_N,i))+1/2| \geq N^{1/16}\big) &\leq \sum_{k\in\mathbb{N}}\frac{2\tilde C e^{\tilde c /2}}{1-e^{-\tilde c}}e^{-\tilde c N^{1/16}}\mathbb{P}\big(\ell^+(T_N,i)=k\big)\\&=\frac{2\tilde C e^{\tilde c /2}}{1-e^{-\tilde c}}e^{-\tilde c N^{1/16}},\end{align*}
which is enough.
We will also need the following, which is a fairly standard result on large deviations.
Lemma 4.
For any
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $\mathbb{P}\Big(\max_{0 \leq i_1 \leq i_2 \leq \lceil N^\alpha\rceil}\left|\sum_{i=i_1}^{i_2}\zeta_i \right| \geq N^{\alpha/2+\varepsilon}\Big)$
tends to 0 when
$\mathbb{P}\Big(\max_{0 \leq i_1 \leq i_2 \leq \lceil N^\alpha\rceil}\left|\sum_{i=i_1}^{i_2}\zeta_i \right| \geq N^{\alpha/2+\varepsilon}\Big)$
tends to 0 when
![]() $N \to +\infty$
.
$N \to +\infty$
.
Proof. Let
![]() $0 \leq i_1 \leq i_2 \leq \lceil N^\alpha\rceil$
, and let us study
$0 \leq i_1 \leq i_2 \leq \lceil N^\alpha\rceil$
, and let us study
![]() $\mathbb{P}\Big(\left|\sum_{i=i_1}^{i_2}\zeta_i \right| \geq N^{\alpha/2+\varepsilon}\Big)$
. We know the
$\mathbb{P}\Big(\left|\sum_{i=i_1}^{i_2}\zeta_i \right| \geq N^{\alpha/2+\varepsilon}\Big)$
. We know the
![]() $\zeta_i$
,
$\zeta_i$
,
![]() $i\in\mathbb{Z}$
, are i.i.d. with distribution
$i\in\mathbb{Z}$
, are i.i.d. with distribution
![]() $\rho_0$
, and it can be checked that
$\rho_0$
, and it can be checked that
![]() $\rho_0$
is symmetric with respect to 0, so from that and the Markov inequality we get
$\rho_0$
is symmetric with respect to 0, so from that and the Markov inequality we get
 \begin{equation} \begin{split} &\qquad\qquad\qquad\mathbb{P}\left(\left|\sum_{i=i_1}^{i_2}\zeta_i\right| \geq N^{\alpha/2+\varepsilon}\right) \leq 2 \mathbb{P}\left(\sum_{i=i_1}^{i_2}\zeta_i \geq N^{\alpha/2+\varepsilon}\right) \\ &=2\mathbb{P}\left(\exp\left(\frac{1}{N^{\alpha/2}}\sum_{i=i_1}^{i_2}\zeta_i\right) \geq \exp(N^{\varepsilon})\right) \leq 2e^{-N^{\varepsilon}}\mathbb{E}\left(\exp\left(\frac{1}{N^{\alpha/2}}\sum_{i=i_1}^{i_2}\zeta_i\right)\right)\\ &\qquad\qquad\qquad\qquad\quad\leq 2e^{-N^{\varepsilon}}\prod_{i=i_1}^{i_2}\mathbb{E}\left(\exp\left(\frac{1}{N^{\alpha/2}}\zeta_i\right)\right). \end{split} \end{equation}
\begin{equation} \begin{split} &\qquad\qquad\qquad\mathbb{P}\left(\left|\sum_{i=i_1}^{i_2}\zeta_i\right| \geq N^{\alpha/2+\varepsilon}\right) \leq 2 \mathbb{P}\left(\sum_{i=i_1}^{i_2}\zeta_i \geq N^{\alpha/2+\varepsilon}\right) \\ &=2\mathbb{P}\left(\exp\left(\frac{1}{N^{\alpha/2}}\sum_{i=i_1}^{i_2}\zeta_i\right) \geq \exp(N^{\varepsilon})\right) \leq 2e^{-N^{\varepsilon}}\mathbb{E}\left(\exp\left(\frac{1}{N^{\alpha/2}}\sum_{i=i_1}^{i_2}\zeta_i\right)\right)\\ &\qquad\qquad\qquad\qquad\quad\leq 2e^{-N^{\varepsilon}}\prod_{i=i_1}^{i_2}\mathbb{E}\left(\exp\left(\frac{1}{N^{\alpha/2}}\zeta_i\right)\right). \end{split} \end{equation}
Now, if
![]() $\zeta$
has distribution
$\zeta$
has distribution
![]() $\rho_0$
, we can write
$\rho_0$
, we can write
with
![]() $|\zeta^{\prime}|\leq|\zeta|$
. Since
$|\zeta^{\prime}|\leq|\zeta|$
. Since
![]() $\rho_0$
is symmetric with respect to 0, we have
$\rho_0$
is symmetric with respect to 0, we have
![]() $\mathbb{E}(\zeta)=0$
; therefore
$\mathbb{E}(\zeta)=0$
; therefore
 \begin{equation*} \mathbb{E}\left(\exp\left(\frac{1}{N^{\alpha/2}}\zeta\right)\right) = 1+\mathbb{E}\left(\frac{1}{2}\left(\frac{1}{N^{\alpha/2}}\zeta\right)^2\exp\left(\frac{1}{N^{\alpha/2}}\zeta^{\prime}\right)\right) \end{equation*}
\begin{equation*} \mathbb{E}\left(\exp\left(\frac{1}{N^{\alpha/2}}\zeta\right)\right) = 1+\mathbb{E}\left(\frac{1}{2}\left(\frac{1}{N^{\alpha/2}}\zeta\right)^2\exp\left(\frac{1}{N^{\alpha/2}}\zeta^{\prime}\right)\right) \end{equation*}
Moreover,
![]() $\rho_0$
has exponential tails; hence there exist constants
$\rho_0$
has exponential tails; hence there exist constants
![]() $C<+\infty$
and
$C<+\infty$
and
![]() $c>0$
such that
$c>0$
such that
![]() $\mathbb{E}\big(\zeta^2e^{c \,|\zeta|}\big) \leq C$
. When N is large enough,
$\mathbb{E}\big(\zeta^2e^{c \,|\zeta|}\big) \leq C$
. When N is large enough,
![]() $\frac{1}{N^{\alpha/2}} \leq c$
; therefore
$\frac{1}{N^{\alpha/2}} \leq c$
; therefore
Together with (5), this yields
 \begin{equation*}\mathbb{P}\left(\left|\sum_{i=i_1}^{i_2}\zeta_i \right| \geq N^{\alpha/2+\varepsilon}\right)\leq 2e^{-N^{\varepsilon}}e^{(i_2-i_1+1)\frac{C}{2N^\alpha}} \leq 2e^{-N^{\varepsilon}}e^{\big(\lceil N^\alpha\rceil+1\big)\frac{C}{2N^\alpha}} \leq 2e^{C}e^{-N^{\varepsilon}}\end{equation*}
\begin{equation*}\mathbb{P}\left(\left|\sum_{i=i_1}^{i_2}\zeta_i \right| \geq N^{\alpha/2+\varepsilon}\right)\leq 2e^{-N^{\varepsilon}}e^{(i_2-i_1+1)\frac{C}{2N^\alpha}} \leq 2e^{-N^{\varepsilon}}e^{\big(\lceil N^\alpha\rceil+1\big)\frac{C}{2N^\alpha}} \leq 2e^{C}e^{-N^{\varepsilon}}\end{equation*}
when N is large enough. We deduce that when N is large enough,
 \begin{equation*}\mathbb{P} \left(\max_{0 \leq i_1 \leq i_2 \leq \lceil N^\alpha\rceil} \left|\sum_{i=i_1}^{i_2}\zeta_i \right| \geq N^{\alpha/2+\varepsilon}\right) \leq (\lceil N^\alpha\rceil+1)^2 2e^{C}e^{-N^{\varepsilon}},\end{equation*}
\begin{equation*}\mathbb{P} \left(\max_{0 \leq i_1 \leq i_2 \leq \lceil N^\alpha\rceil} \left|\sum_{i=i_1}^{i_2}\zeta_i \right| \geq N^{\alpha/2+\varepsilon}\right) \leq (\lceil N^\alpha\rceil+1)^2 2e^{C}e^{-N^{\varepsilon}},\end{equation*}
which tends to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
We also prove an immediate application of Lemma 4, which we will use several times. If we define
 \begin{equation*} \mathcal{B}_3^{-}=\left\{\max_{-\lfloor (|x|+2\theta)N\rfloor-N^{3/4} \leq i_1 \leq i_2 \leq -\lfloor (|x|+2\theta)N\rfloor+N^{3/4}} \left|\sum_{i=i_1}^{i_2} \zeta_i\right| \geq N^{19/48}\right\}, \end{equation*}
\begin{equation*} \mathcal{B}_3^{-}=\left\{\max_{-\lfloor (|x|+2\theta)N\rfloor-N^{3/4} \leq i_1 \leq i_2 \leq -\lfloor (|x|+2\theta)N\rfloor+N^{3/4}} \left|\sum_{i=i_1}^{i_2} \zeta_i\right| \geq N^{19/48}\right\}, \end{equation*}
 \begin{equation*} \mathcal{B}_3^+=\left\{\max_{\lfloor (|x|+2\theta)N\rfloor-N^{3/4} \leq i_1 \leq i_2 \leq \lfloor (|x|+2\theta)N\rfloor+N^{3/4}} \left|\sum_{i=i_1}^{i_2} \zeta_i\right| \geq N^{19/48}\right\},\end{equation*}
\begin{equation*} \mathcal{B}_3^+=\left\{\max_{\lfloor (|x|+2\theta)N\rfloor-N^{3/4} \leq i_1 \leq i_2 \leq \lfloor (|x|+2\theta)N\rfloor+N^{3/4}} \left|\sum_{i=i_1}^{i_2} \zeta_i\right| \geq N^{19/48}\right\},\end{equation*}
we have the following lemma.
Lemma 5.
![]() $\mathbb{P}\big(\mathcal{B}_3^{-}\big)$
and
$\mathbb{P}\big(\mathcal{B}_3^{-}\big)$
and
![]() $\mathbb{P}\big(\mathcal{B}_3^+\big)$
tend to 0 when N tends to
$\mathbb{P}\big(\mathcal{B}_3^+\big)$
tend to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
Proof. Since the
![]() $(\zeta_i)_{i\in\mathbb{Z}}$
are i.i.d.,
$(\zeta_i)_{i\in\mathbb{Z}}$
are i.i.d.,
 \begin{equation*}\mathbb{P}\big(\mathcal{B}_3^+\big)=\mathbb{P}\big(\mathcal{B}_3^{-}\big)=\mathbb{P}\left(\max_{0 \leq i_1 \leq i_2 \leq 2 \lceil N^{3/4} \rceil} \left|\sum_{i=i_1}^{i_2} \zeta_i \right| \geq N^{19/48}\right),\end{equation*}
\begin{equation*}\mathbb{P}\big(\mathcal{B}_3^+\big)=\mathbb{P}\big(\mathcal{B}_3^{-}\big)=\mathbb{P}\left(\max_{0 \leq i_1 \leq i_2 \leq 2 \lceil N^{3/4} \rceil} \left|\sum_{i=i_1}^{i_2} \zeta_i \right| \geq N^{19/48}\right),\end{equation*}
which is smaller than
![]() $\mathbb{P}\Big(\max_{0 \leq i_1 \leq i_2 \leq \lceil N^{37/48} \rceil} \Big|\sum_{i=i_1}^{i_2} \zeta_i\Big| \geq N^{19/48}\Big)$
when N is large enough. Moreover, Lemma 4, used with
$\mathbb{P}\Big(\max_{0 \leq i_1 \leq i_2 \leq \lceil N^{37/48} \rceil} \Big|\sum_{i=i_1}^{i_2} \zeta_i\Big| \geq N^{19/48}\Big)$
when N is large enough. Moreover, Lemma 4, used with
![]() $\alpha=37/48$
and
$\alpha=37/48$
and
![]() $\varepsilon=1/96$
, yields that the latter probability tends to 0 when N tends to
$\varepsilon=1/96$
, yields that the latter probability tends to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
3. Where the local times approach 0
The aim of this section is twofold. Firstly, we need to control the place where
![]() $\ell^{-}(T_N,i)$
hits 0 when i is to the right of 0, as well as the place where
$\ell^{-}(T_N,i)$
hits 0 when i is to the right of 0, as well as the place where
![]() $\ell^+(T_N,i)$
hits 0 when i is to the left of 0. Secondly, we have to show that even when
$\ell^+(T_N,i)$
hits 0 when i is to the left of 0. Secondly, we have to show that even when
![]() $\ell^\pm(T_N,i)$
is close to 0, the local times do not stray too far away from the coupling. For any
$\ell^\pm(T_N,i)$
is close to 0, the local times do not stray too far away from the coupling. For any
![]() $N \in \mathbb{N}$
, we define
$N \in \mathbb{N}$
, we define
![]() $I^+=\inf\{i \geq \chi(N)\,|\,\ell^{-}(T_N,i)=0\}$
and
$I^+=\inf\{i \geq \chi(N)\,|\,\ell^{-}(T_N,i)=0\}$
and
![]() $I^{-}=\sup\{i < \chi(N)\,|\,\ell^+(T_N,i)=0\}$
. We notice that
$I^{-}=\sup\{i < \chi(N)\,|\,\ell^+(T_N,i)=0\}$
. We notice that
![]() $\ell^+(T_N,I^{-}) = 0$
, and from the definition of
$\ell^+(T_N,I^{-}) = 0$
, and from the definition of
![]() $T_N$
we have
$T_N$
we have
![]() $\ell^+(T_N,i) > 0$
for any
$\ell^+(T_N,i) > 0$
for any
![]() $0 \leq i \leq \chi(N)-1$
; hence
$0 \leq i \leq \chi(N)-1$
; hence
![]() $I^{-}<0$
. We first state an elementary result that we will use many times in this work.
$I^{-}<0$
. We first state an elementary result that we will use many times in this work.
Lemma 6.
For any
![]() $i \geq I^+$
or
$i \geq I^+$
or
![]() $i \leq I^{-}$
we have
$i \leq I^{-}$
we have
![]() $\ell^\pm(T_N,i)=0$
.
$\ell^\pm(T_N,i)=0$
.
Proof. Since
![]() $\ell^+(T_N,I^{-}) = 0$
and the random walk is at
$\ell^+(T_N,I^{-}) = 0$
and the random walk is at
![]() $\lfloor Nx \rfloor \iota1>0$
at time
$\lfloor Nx \rfloor \iota1>0$
at time
![]() $T_N$
, the random walk did not reach
$T_N$
, the random walk did not reach
![]() $I^{-}$
before time
$I^{-}$
before time
![]() $T_N$
; thus
$T_N$
; thus
![]() $\ell^\pm(T_N,i)=0$
for any
$\ell^\pm(T_N,i)=0$
for any
![]() $i \leq I^{-}$
. Moreover,
$i \leq I^{-}$
. Moreover,
![]() $\ell^{-}(T_N,\chi(N)) > 0$
by definition of
$\ell^{-}(T_N,\chi(N)) > 0$
by definition of
![]() $T_N$
, so
$T_N$
, so
![]() $I^+>\chi(N)$
; thus
$I^+>\chi(N)$
; thus
![]() $X_{T_N} < I^+$
, and hence
$X_{T_N} < I^+$
, and hence
![]() $\ell^{-}(T_N,I^+) = 0$
implies that the random walk did not reach
$\ell^{-}(T_N,I^+) = 0$
implies that the random walk did not reach
![]() $I^+$
before time
$I^+$
before time
![]() $T_N$
. Thus
$T_N$
. Thus
![]() $\ell^\pm(T_N,i)=0$
for any
$\ell^\pm(T_N,i)=0$
for any
![]() $i \geq I^+$
.
$i \geq I^+$
.
We will also need the auxiliary random variables
![]() ${\tilde{I}}^+=\inf\{i \geq \chi(N)\,|\,\ell^{-}(T_N,i)\leq\big\lfloor N^{1/6}\big\rfloor\}$
and
${\tilde{I}}^+=\inf\{i \geq \chi(N)\,|\,\ell^{-}(T_N,i)\leq\big\lfloor N^{1/6}\big\rfloor\}$
and
![]() ${\tilde{I}}^{-}=\sup\big\{i < \chi(N)\,|\,\ell^+(T_N,i)\leq\big\lfloor N^{1/6}\big\rfloor\big\}$
.
${\tilde{I}}^{-}=\sup\big\{i < \chi(N)\,|\,\ell^+(T_N,i)\leq\big\lfloor N^{1/6}\big\rfloor\big\}$
.
3.1. Place where we hit 0
We have the following result on the control of
![]() $I^+$
and
$I^+$
and
![]() $I^{-}$
.
$I^{-}$
.
Lemma 7.
For any
![]() $\delta>0$
,
$\delta>0$
,
![]() $\mathbb{P}\big(|I^{-}+(|x|+2\theta)N| \geq N^{\delta+1/2}\big)$
and
$\mathbb{P}\big(|I^{-}+(|x|+2\theta)N| \geq N^{\delta+1/2}\big)$
and
![]() $\mathbb{P}(|I^+-(|x|+2\theta)N| \geq N^{\delta+1/2})$
tend to 0 when N tends to
$\mathbb{P}(|I^+-(|x|+2\theta)N| \geq N^{\delta+1/2})$
tend to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
Proof. The idea is to control the fluctuations of the local times around their deterministic limit: as long as
![]() $\ell^\pm(T_N,i)$
is large, the
$\ell^\pm(T_N,i)$
is large, the
![]() $\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
will be close to the i.i.d. random variables of the coupling, so the fluctuations of
$\ell^\pm(T_N,i+1)-\ell^\pm(T_N,i)$
will be close to the i.i.d. random variables of the coupling, so the fluctuations of
![]() $\ell^\pm(T_N,i)$
around its deterministic limit are bounded and
$\ell^\pm(T_N,i)$
around its deterministic limit are bounded and
![]() $\ell^\pm(T_N,i)$
can be small only when the deterministic limit is small, that is, around
$\ell^\pm(T_N,i)$
can be small only when the deterministic limit is small, that is, around
![]() $-(|x|+2\theta)N$
and
$-(|x|+2\theta)N$
and
![]() $(|x|+2\theta)N$
. We spell out the proof only for
$(|x|+2\theta)N$
. We spell out the proof only for
![]() $I^{-}$
, as the argument for
$I^{-}$
, as the argument for
![]() $I^+$
is similar.
$I^+$
is similar.
The fact that
![]() $\mathbb{P}\big(I^{-}+(|x|+2\theta)N \leq -N^{\delta+1/2}\big)$
tends to 0 when N tends to
$\mathbb{P}\big(I^{-}+(|x|+2\theta)N \leq -N^{\delta+1/2}\big)$
tends to 0 when N tends to
![]() $+\infty$
comes from the inequalities (51) and (53) in [Reference Tóth and Vető17], so we only have to prove that
$+\infty$
comes from the inequalities (51) and (53) in [Reference Tóth and Vető17], so we only have to prove that
![]() $\mathbb{P}(I^{-}+(|x|+2\theta)N \geq N^{\delta+1/2})$
tends to 0 when N tends to
$\mathbb{P}(I^{-}+(|x|+2\theta)N \geq N^{\delta+1/2})$
tends to 0 when N tends to
![]() $+\infty$
. Since
$+\infty$
. Since
![]() $I^{-} \leq {\tilde{I}}^{-}$
, it is enough to prove that
$I^{-} \leq {\tilde{I}}^{-}$
, it is enough to prove that
![]() $\mathbb{P}({\tilde{I}}^{-}+(|x|+2\theta)N \geq N^{\delta+1/2})$
tends to 0 when N tends to
$\mathbb{P}({\tilde{I}}^{-}+(|x|+2\theta)N \geq N^{\delta+1/2})$
tends to 0 when N tends to
![]() $+\infty$
. Since by Lemma 2 we have that
$+\infty$
. Since by Lemma 2 we have that
![]() $\mathbb{P}\big(\mathcal{B}_1^{-}\big)$
tends to 0 when N tends to
$\mathbb{P}\big(\mathcal{B}_1^{-}\big)$
tends to 0 when N tends to
![]() $+\infty$
, it is enough to prove that
$+\infty$
, it is enough to prove that
![]() $\mathbb{P}({\tilde{I}}^{-}+(|x|+2\theta)N \geq N^{\delta+1/2},\big(\mathcal{B}_1^{-}\big)^c)$
tends to 0 when N tends to
$\mathbb{P}({\tilde{I}}^{-}+(|x|+2\theta)N \geq N^{\delta+1/2},\big(\mathcal{B}_1^{-}\big)^c)$
tends to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
We now assume N is large enough,
![]() ${\tilde{I}}^{-}+(|x|+2\theta)N \geq N^{\delta+1/2}$
, and
${\tilde{I}}^{-}+(|x|+2\theta)N \geq N^{\delta+1/2}$
, and
![]() $\big(\mathcal{B}_1^{-}\big)^c$
. Then there exists
$\big(\mathcal{B}_1^{-}\big)^c$
. Then there exists
![]() $i\in\{\lceil-(|x|+2\theta)N+N^{\delta+1/2}\rceil,\ldots,\chi(N)-1\}$
such that
$i\in\{\lceil-(|x|+2\theta)N+N^{\delta+1/2}\rceil,\ldots,\chi(N)-1\}$
such that
![]() $\ell^+(T_N,i) \leq \big\lfloor N^{1/6}\big\rfloor$
and
$\ell^+(T_N,i) \leq \big\lfloor N^{1/6}\big\rfloor$
and
![]() $\ell^+(T_N,j) > \big\lfloor N^{1/6}\big\rfloor$
for all
$\ell^+(T_N,j) > \big\lfloor N^{1/6}\big\rfloor$
for all
![]() $j \in\{i+1,\ldots,\chi(N)-1\}$
. Thus, by (1) we get
$j \in\{i+1,\ldots,\chi(N)-1\}$
. Thus, by (1) we get
 \begin{equation*}\lfloor N \theta\rfloor+\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}(\ell^+(T_N,j))+\mathbb{1}_{\{j > 0\}}\big)=\ell^+(T_N,i) \leq \big\lfloor N^{1/6}\big\rfloor.\end{equation*}
\begin{equation*}\lfloor N \theta\rfloor+\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}(\ell^+(T_N,j))+\mathbb{1}_{\{j > 0\}}\big)=\ell^+(T_N,i) \leq \big\lfloor N^{1/6}\big\rfloor.\end{equation*}
Furthermore, for all
![]() $j \in\{i+1,\ldots,\chi(N)-1\}$
, since
$j \in\{i+1,\ldots,\chi(N)-1\}$
, since
![]() $\big(\mathcal{B}_1^{-}\big)^c$
occurs and
$\big(\mathcal{B}_1^{-}\big)^c$
occurs and
![]() $\ell^+(T_N,j) > \big\lfloor N^{1/6}\big\rfloor$
, we have
$\ell^+(T_N,j) > \big\lfloor N^{1/6}\big\rfloor$
, we have
![]() $\eta_{j,-}(\ell^+(T_N,j))+1/2=\zeta_j$
. We deduce that
$\eta_{j,-}(\ell^+(T_N,j))+1/2=\zeta_j$
. We deduce that
 \begin{equation*}\lfloor N \theta\rfloor + \sum_{j=i+1}^{\chi(N)-1} \left(\zeta_j+\frac{\mathbb{1}_{\{j > 0\}}-\mathbb{1}_{\{j \leq 0\}}}{2}\right) \leq \lfloor N^{1/6}\rfloor;\end{equation*}
\begin{equation*}\lfloor N \theta\rfloor + \sum_{j=i+1}^{\chi(N)-1} \left(\zeta_j+\frac{\mathbb{1}_{\{j > 0\}}-\mathbb{1}_{\{j \leq 0\}}}{2}\right) \leq \lfloor N^{1/6}\rfloor;\end{equation*}
thus
 \begin{equation*}\sum_{j=i+1}^{\chi(N)-1}\zeta_j+\lfloor N \theta\rfloor+\sum_{j=i+1}^{\chi(N)-1}\frac{\mathbb{1}_{\{j > 0\}}-\mathbb{1}_{\{j \leq 0\}}}{2}\leq \lfloor N^{1/6}\rfloor.\end{equation*}
\begin{equation*}\sum_{j=i+1}^{\chi(N)-1}\zeta_j+\lfloor N \theta\rfloor+\sum_{j=i+1}^{\chi(N)-1}\frac{\mathbb{1}_{\{j > 0\}}-\mathbb{1}_{\{j \leq 0\}}}{2}\leq \lfloor N^{1/6}\rfloor.\end{equation*}
Moreover, since
![]() $i \in\{\lceil-(|x|+2\theta)N+N^{\delta+1/2}\rceil,\ldots,\chi(N)-1\}$
, we have
$i \in\{\lceil-(|x|+2\theta)N+N^{\delta+1/2}\rceil,\ldots,\chi(N)-1\}$
, we have
 \begin{align*}\sum_{j=i+1}^{\chi(N)-1}\frac{\mathbb{1}_{\{j > 0\}}-\mathbb{1}_{\{j \leq 0\}}}{2} &=\frac{1}{2}(\chi(N)-1+i) \\&\geq \frac{1}{2}\big(Nx-2-(|x|+2\theta)N+N^{\delta+1/2}\big)\\&=-\theta N+\frac{1}{2}N^{\delta+1/2}-1.\end{align*}
\begin{align*}\sum_{j=i+1}^{\chi(N)-1}\frac{\mathbb{1}_{\{j > 0\}}-\mathbb{1}_{\{j \leq 0\}}}{2} &=\frac{1}{2}(\chi(N)-1+i) \\&\geq \frac{1}{2}\big(Nx-2-(|x|+2\theta)N+N^{\delta+1/2}\big)\\&=-\theta N+\frac{1}{2}N^{\delta+1/2}-1.\end{align*}
This yields
![]() $\sum_{j=i+1}^{\chi(N)-1}\zeta_j+\lfloor N \theta\rfloor-\theta N+\frac{1}{2}N^{\delta+1/2}-1 \leq \big\lfloor N^{1/6}\big\rfloor$
; hence
$\sum_{j=i+1}^{\chi(N)-1}\zeta_j+\lfloor N \theta\rfloor-\theta N+\frac{1}{2}N^{\delta+1/2}-1 \leq \big\lfloor N^{1/6}\big\rfloor$
; hence
 \begin{equation*}\sum_{j=i+1}^{\chi(N)-1}\zeta_j \leq -\frac{1}{2}N^{\delta+1/2}+\big\lfloor N^{1/6}\big\rfloor+2 \leq -N^{(1+\delta)/2}\end{equation*}
\begin{equation*}\sum_{j=i+1}^{\chi(N)-1}\zeta_j \leq -\frac{1}{2}N^{\delta+1/2}+\big\lfloor N^{1/6}\big\rfloor+2 \leq -N^{(1+\delta)/2}\end{equation*}
since N is large enough. Consequently, when N is large enough,
 \begin{align*}&\mathbb{P}\big({\tilde{I}}^{-}+(|x|+2\theta)N \geq N^{\delta+1/2},\big(\mathcal{B}_1^{-}\big)^c\big) \\& \qquad \leq \mathbb{P} \left(\exists\, i\in\{\lceil-(|x|+2\theta)N+N^{\delta+1/2}\rceil,\ldots,\chi(N)-1\}, \sum_{j=i+1}^{\chi(N)-1}\zeta_j \leq -N^{(1+\delta)/2} \right).\end{align*}
\begin{align*}&\mathbb{P}\big({\tilde{I}}^{-}+(|x|+2\theta)N \geq N^{\delta+1/2},\big(\mathcal{B}_1^{-}\big)^c\big) \\& \qquad \leq \mathbb{P} \left(\exists\, i\in\{\lceil-(|x|+2\theta)N+N^{\delta+1/2}\rceil,\ldots,\chi(N)-1\}, \sum_{j=i+1}^{\chi(N)-1}\zeta_j \leq -N^{(1+\delta)/2} \right).\end{align*}
Since the
![]() $\zeta_i$
,
$\zeta_i$
,
![]() $i\in\mathbb{Z}$
, are i.i.d., when N is large enough this yields
$i\in\mathbb{Z}$
, are i.i.d., when N is large enough this yields
 \begin{equation*}\mathbb{P}\big({\tilde{I}}^{-}+(|x|+2\theta)N \geq N^{\delta+1/2},\big(\mathcal{B}_1^{-}\big)^c\big) \leq \mathbb{P}\left(\max_{0 \leq i_1 \leq i_2 \leq \lceil N^{1+\delta/2}\rceil}\left|\sum_{i=i_1}^{i_2}\zeta_i\right|\geq N^{(1+\delta)/2}\right),\end{equation*}
\begin{equation*}\mathbb{P}\big({\tilde{I}}^{-}+(|x|+2\theta)N \geq N^{\delta+1/2},\big(\mathcal{B}_1^{-}\big)^c\big) \leq \mathbb{P}\left(\max_{0 \leq i_1 \leq i_2 \leq \lceil N^{1+\delta/2}\rceil}\left|\sum_{i=i_1}^{i_2}\zeta_i\right|\geq N^{(1+\delta)/2}\right),\end{equation*}
which tends to 0 when N tends to
![]() $+\infty$
by Lemma 4 (applied with
$+\infty$
by Lemma 4 (applied with
![]() $\alpha=1+\delta/2$
and
$\alpha=1+\delta/2$
and
![]() $\varepsilon=\delta/4$
). This shows that
$\varepsilon=\delta/4$
). This shows that
![]() $\mathbb{P}\big(I^{-}+(|x|+2\theta)N \geq N^{\delta+1/2}\big)$
converges to 0 when N tends to
$\mathbb{P}\big(I^{-}+(|x|+2\theta)N \geq N^{\delta+1/2}\big)$
converges to 0 when N tends to
![]() $+\infty$
, which completes the proof of Lemma 7.
$+\infty$
, which completes the proof of Lemma 7.
3.2. Control of low local times
We have to show that even when
![]() $\ell^\pm(T_N,i)$
is small, the local times are not too far from the random variables of the coupling. In order to do that, we first prove that the window where
$\ell^\pm(T_N,i)$
is small, the local times are not too far from the random variables of the coupling. In order to do that, we first prove that the window where
![]() $\ell^\pm(T_N,i)$
is small but not zero—that is, between
$\ell^\pm(T_N,i)$
is small but not zero—that is, between
![]() ${\tilde{I}}^+$
and
${\tilde{I}}^+$
and
![]() $I^+$
and between
$I^+$
and between
![]() $I^{-}$
and
$I^{-}$
and
![]() ${\tilde{I}}^{-}$
—is small. Afterwards, we will give bounds on what happens inside. We begin by showing the following easy result.
${\tilde{I}}^{-}$
—is small. Afterwards, we will give bounds on what happens inside. We begin by showing the following easy result.
Lemma 8.
![]() $\mathbb{P}({\tilde{I}}^{-} \geq 0)$
tends to 0 when
$\mathbb{P}({\tilde{I}}^{-} \geq 0)$
tends to 0 when
![]() $N \to +\infty$
.
$N \to +\infty$
.
Proof. Let N be large enough. If
![]() ${\tilde{I}}^{-} \geq 0$
, there exists
${\tilde{I}}^{-} \geq 0$
, there exists
![]() $i\in\{0,\ldots,\lfloor Nx\rfloor\}$
such that
$i\in\{0,\ldots,\lfloor Nx\rfloor\}$
such that
![]() $\ell^+(T_N,i)\leq\big\lfloor N^{1/6}\big\rfloor$
. Since N is large enough, this implies
$\ell^+(T_N,i)\leq\big\lfloor N^{1/6}\big\rfloor$
. Since N is large enough, this implies
![]() $\ell^+(T_N,i)\leq N\theta/2$
; therefore
$\ell^+(T_N,i)\leq N\theta/2$
; therefore
Moreover, by [Reference Tóth and Vető17, Theorem 1],
![]() $\sup_{y \in \mathbb{R}}\big|\frac{1}{N}\ell^+\big(T_N,\lfloor N y\rfloor\big)-\Big(\frac{|x|-|y|}{2}+\theta\Big)_+\big|$
converges in probability to 0 when N tends to
$\sup_{y \in \mathbb{R}}\big|\frac{1}{N}\ell^+\big(T_N,\lfloor N y\rfloor\big)-\Big(\frac{|x|-|y|}{2}+\theta\Big)_+\big|$
converges in probability to 0 when N tends to
![]() $+\infty$
; hence we deduce that
$+\infty$
; hence we deduce that
 \begin{equation*}\mathbb{P}\left(\sup_{y \in \mathbb{R}}\left|\frac{1}{N}\ell^+\big(T_N,\lfloor N y\rfloor\big)-\left(\frac{|x|-|y|}{2}+\theta\right)_+ \right| \geq \theta/2\right)\end{equation*}
\begin{equation*}\mathbb{P}\left(\sup_{y \in \mathbb{R}}\left|\frac{1}{N}\ell^+\big(T_N,\lfloor N y\rfloor\big)-\left(\frac{|x|-|y|}{2}+\theta\right)_+ \right| \geq \theta/2\right)\end{equation*}
tends to 0 when
![]() $N \to +\infty$
. Therefore
$N \to +\infty$
. Therefore
![]() $\mathbb{P}({\tilde{I}}^{-} \geq 0)$
tends to 0 when
$\mathbb{P}({\tilde{I}}^{-} \geq 0)$
tends to 0 when
![]() $N \to +\infty$
.
$N \to +\infty$
.
In order to control
![]() $I^+$
,
$I^+$
,
![]() $I^{-}$
,
$I^{-}$
,
![]() ${\tilde{I}}^+$
, and
${\tilde{I}}^+$
, and
![]() ${\tilde{I}}^{-}$
, we will use the fact that the local times behave as the Markov chain L from [Reference Tóth and Vető17], defined as follows. We consider i.i.d. copies of the Markov chain
${\tilde{I}}^{-}$
, we will use the fact that the local times behave as the Markov chain L from [Reference Tóth and Vető17], defined as follows. We consider i.i.d. copies of the Markov chain
![]() $\eta$
starting at 0, called
$\eta$
starting at 0, called
![]() $(\eta_m)_{m\in\mathbb{N}}$
. For any
$(\eta_m)_{m\in\mathbb{N}}$
. For any
![]() $m\in\mathbb{N}$
, we then set
$m\in\mathbb{N}$
, we then set
![]() $L(m+1)=L(m)+\eta_{m}(L(m))$
. We let
$L(m+1)=L(m)+\eta_{m}(L(m))$
. We let
![]() $\tau=\inf\{m\in\mathbb{N}\,|\,L(m) \leq 0\}$
. The following was proven in [Reference Tóth and Vető17].
$\tau=\inf\{m\in\mathbb{N}\,|\,L(m) \leq 0\}$
. The following was proven in [Reference Tóth and Vető17].
Lemma 9. ([Reference Tóth and Vető17, Lemma 2].) There exists a constant
![]() $K < +\infty$
such that for any
$K < +\infty$
such that for any
![]() $k\in \mathbb{N}$
we have
$k\in \mathbb{N}$
we have
![]() $\mathbb{E}(\tau|L(0)=k) \leq 3k+K$
.
$\mathbb{E}(\tau|L(0)=k) \leq 3k+K$
.
Since the local times will behave as L, Lemma 9 implies that if the local time starts out small, then the time at which it reaches 0 has small expectation and hence is not too large. This will help us to prove the following control on the window where
![]() $\ell^\pm(T_N,i)$
is small but not zero.
$\ell^\pm(T_N,i)$
is small but not zero.
Lemma 10.
![]() $\mathbb{P}\big(I^+-{\tilde{I}}^+ \geq N^{1/4}\big)$
and
$\mathbb{P}\big(I^+-{\tilde{I}}^+ \geq N^{1/4}\big)$
and
![]() $\mathbb{P}\big({\tilde{I}}^{-}-I^{-} \geq N^{1/4}\big)$
tend to 0 when
$\mathbb{P}\big({\tilde{I}}^{-}-I^{-} \geq N^{1/4}\big)$
tend to 0 when
![]() $N \to +\infty$
.
$N \to +\infty$
.
Proof. Let N be large enough. We deal only with
![]() $\mathbb{P}\big({\tilde{I}}^{-}-I^{-} \geq N^{1/4}\big)$
, since
$\mathbb{P}\big({\tilde{I}}^{-}-I^{-} \geq N^{1/4}\big)$
, since
![]() $\mathbb{P}\big(I^+-{\tilde{I}}^+ \geq N^{1/4}\big)$
can be dealt with in the same way and with simpler arguments. Thanks to Lemma 8, it is enough to prove that
$\mathbb{P}\big(I^+-{\tilde{I}}^+ \geq N^{1/4}\big)$
can be dealt with in the same way and with simpler arguments. Thanks to Lemma 8, it is enough to prove that
![]() $\mathbb{P}\big({\tilde{I}}^{-}-I^{-} \geq N^{1/4},{\tilde{I}}^{-}<0\big)$
tends to 0 when
$\mathbb{P}\big({\tilde{I}}^{-}-I^{-} \geq N^{1/4},{\tilde{I}}^{-}<0\big)$
tends to 0 when
![]() $N \to +\infty$
. Moreover, if
$N \to +\infty$
. Moreover, if
![]() ${\tilde{I}}^{-} < 0$
, thanks to (1), for any
${\tilde{I}}^{-} < 0$
, thanks to (1), for any
![]() $i < {\tilde{I}}^{-}$
we get
$i < {\tilde{I}}^{-}$
we get
![]() $\ell^+(T_N,i)=\ell^+(T_N,{\tilde{I}}^{-})+\sum_{j=i+1}^{{\tilde{I}}^{-}}\eta_{j,-}(\ell^+(T_N,j))$
, which allows us to prove that
$\ell^+(T_N,i)=\ell^+(T_N,{\tilde{I}}^{-})+\sum_{j=i+1}^{{\tilde{I}}^{-}}\eta_{j,-}(\ell^+(T_N,j))$
, which allows us to prove that
![]() $(\ell^+(T_N,{\tilde{I}}^{-}-i))_{i \in \mathbb{N}}$
is a Markov chain with the transition probabilities of L. Therefore, recalling the notation just before Lemma 9, we have
$(\ell^+(T_N,{\tilde{I}}^{-}-i))_{i \in \mathbb{N}}$
is a Markov chain with the transition probabilities of L. Therefore, recalling the notation just before Lemma 9, we have
 \begin{equation*} =\sum_{k=0}^{\lfloor N^{1/6} \rfloor}\mathbb{P}\left({\tilde{I}}^{-}-I^{-} \geq N^{1/4},{\tilde{I}}^{-}<0\left|\ell^+(T_N,{\tilde{I}}^{-})=k\right.\right)\mathbb{P}\left(\ell^+(T_N,{\tilde{I}}^{-})=k\right) \end{equation*}
\begin{equation*} =\sum_{k=0}^{\lfloor N^{1/6} \rfloor}\mathbb{P}\left({\tilde{I}}^{-}-I^{-} \geq N^{1/4},{\tilde{I}}^{-}<0\left|\ell^+(T_N,{\tilde{I}}^{-})=k\right.\right)\mathbb{P}\left(\ell^+(T_N,{\tilde{I}}^{-})=k\right) \end{equation*}
 \begin{equation*} =\sum_{k=0}^{\lfloor N^{1/6} \rfloor}\mathbb{P}\left(\left.\tau \geq N^{1/4}\right|L(0)=k\right)\mathbb{P}\left(\ell^+(T_N,{\tilde{I}}^{-})=k\right) \end{equation*}
\begin{equation*} =\sum_{k=0}^{\lfloor N^{1/6} \rfloor}\mathbb{P}\left(\left.\tau \geq N^{1/4}\right|L(0)=k\right)\mathbb{P}\left(\ell^+(T_N,{\tilde{I}}^{-})=k\right) \end{equation*}
 \begin{equation*} \leq \sum_{k=0}^{\lfloor N^{1/6} \rfloor}\frac{1}{N^{1/4}}\mathbb{E}(\tau|L(0)=k)\mathbb{P}(\ell^+(T_N,{\tilde{I}}^{-})=k).\end{equation*}
\begin{equation*} \leq \sum_{k=0}^{\lfloor N^{1/6} \rfloor}\frac{1}{N^{1/4}}\mathbb{E}(\tau|L(0)=k)\mathbb{P}(\ell^+(T_N,{\tilde{I}}^{-})=k).\end{equation*}
By Lemma 9 we deduce that
 \begin{equation*} \mathbb{P}\left({\tilde{I}}^{-}-I^{-} \geq N^{1/4},{\tilde{I}}^{-}<0\right) \leq \frac{1}{N^{1/4}}\sum_{k=0}^{\lfloor N^{1/6} \rfloor}(3k+K)\mathbb{P}(\ell^+(T_N,{\tilde{I}}^{-})=k) \end{equation*}
\begin{equation*} \mathbb{P}\left({\tilde{I}}^{-}-I^{-} \geq N^{1/4},{\tilde{I}}^{-}<0\right) \leq \frac{1}{N^{1/4}}\sum_{k=0}^{\lfloor N^{1/6} \rfloor}(3k+K)\mathbb{P}(\ell^+(T_N,{\tilde{I}}^{-})=k) \end{equation*}
since N is large enough; hence
![]() $\mathbb{P}({\tilde{I}}^{-}-I^{-} \geq N^{1/4},{\tilde{I}}^{-}<0)$
tends to 0 when
$\mathbb{P}({\tilde{I}}^{-}-I^{-} \geq N^{1/4},{\tilde{I}}^{-}<0)$
tends to 0 when
![]() $N \to +\infty$
, which completes the proof.
$N \to +\infty$
, which completes the proof.
We are now going to prove that even when
![]() $\ell^\pm(T_N,i)$
is small, the local times are not too far from the random variables of the coupling. More precisely, for any
$\ell^\pm(T_N,i)$
is small, the local times are not too far from the random variables of the coupling. More precisely, for any
![]() $n\in\mathbb{N}$
, we define the following events:
$n\in\mathbb{N}$
, we define the following events:
 \begin{equation*} \mathcal{B}_4^{-}=\left\{\exists \, i \in \{I^{-},\ldots,\chi(N)-1\},\left|\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{\chi(N)-1}\zeta_j\right| \geq N^{1/3} \right\},\end{equation*}
\begin{equation*} \mathcal{B}_4^{-}=\left\{\exists \, i \in \{I^{-},\ldots,\chi(N)-1\},\left|\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{\chi(N)-1}\zeta_j\right| \geq N^{1/3} \right\},\end{equation*}
 \begin{equation*} \mathcal{B}_4^+=\left\{\exists \, i \in \{\chi(N),\ldots,I^+\},\left|\sum_{j=\chi(N)}^{i-1}(\eta_{j,+}(\ell^{-}(T_N,j))+1/2)-\sum_{j=\chi(N)}^{i-1}\zeta_j\right| \geq N^{1/3} \right\}.\end{equation*}
\begin{equation*} \mathcal{B}_4^+=\left\{\exists \, i \in \{\chi(N),\ldots,I^+\},\left|\sum_{j=\chi(N)}^{i-1}(\eta_{j,+}(\ell^{-}(T_N,j))+1/2)-\sum_{j=\chi(N)}^{i-1}\zeta_j\right| \geq N^{1/3} \right\}.\end{equation*}
Lemma 11.
![]() $\mathbb{P}\big(\mathcal{B}_4^{-}\big)$
and
$\mathbb{P}\big(\mathcal{B}_4^{-}\big)$
and
![]() $\mathbb{P}\big(\mathcal{B}_4^+\big)$
tend to 0 when N tend to
$\mathbb{P}\big(\mathcal{B}_4^+\big)$
tend to 0 when N tend to
![]() $+\infty$
.
$+\infty$
.
Proof. The idea of the argument is that when
![]() $\ell^\pm(T_N,i)$
is large,
$\ell^\pm(T_N,i)$
is large,
![]() $\eta_{i,\mp}(\ell^\pm(T_N,i))+1/2=\zeta_i$
thanks to Lemma 2; that the window where
$\eta_{i,\mp}(\ell^\pm(T_N,i))+1/2=\zeta_i$
thanks to Lemma 2; that the window where
![]() $\ell^\pm(T_N,i)$
is small is bounded by Lemma 10; and that inside this window the
$\ell^\pm(T_N,i)$
is small is bounded by Lemma 10; and that inside this window the
![]() $\eta_{i,\mp}(\ell^\pm(T_N,i))+1/2$
,
$\eta_{i,\mp}(\ell^\pm(T_N,i))+1/2$
,
![]() $\zeta_i$
are also bounded by Lemma 3. We spell out the proof only for
$\zeta_i$
are also bounded by Lemma 3. We spell out the proof only for
![]() $\mathbb{P}\big(\mathcal{B}_4^{-}\big)$
, since the proof for
$\mathbb{P}\big(\mathcal{B}_4^{-}\big)$
, since the proof for
![]() $\mathbb{P}\big(\mathcal{B}_4^+\big)$
is the same. By Lemma 7, we have that
$\mathbb{P}\big(\mathcal{B}_4^+\big)$
is the same. By Lemma 7, we have that
![]() $\mathbb{P}(I^{-} \leq -2(|x|+\theta)N)$
tends to 0 when N tends to
$\mathbb{P}(I^{-} \leq -2(|x|+\theta)N)$
tends to 0 when N tends to
![]() $+\infty$
. Furthermore, Lemma 10 implies that
$+\infty$
. Furthermore, Lemma 10 implies that
![]() $\mathbb{P}\big({\tilde{I}}^{-}-I^{-} \geq N^{1/4}\big)$
tends to 0 when N tends to
$\mathbb{P}\big({\tilde{I}}^{-}-I^{-} \geq N^{1/4}\big)$
tends to 0 when N tends to
![]() $+\infty$
. In addition, by Lemmas 2 and 3 we have that
$+\infty$
. In addition, by Lemmas 2 and 3 we have that
![]() $\mathbb{P}\big(\mathcal{B}_1^{-}\big)$
and
$\mathbb{P}\big(\mathcal{B}_1^{-}\big)$
and
![]() $\mathbb{P}(\mathcal{B}_2)$
tend to 0 when N tends to
$\mathbb{P}(\mathcal{B}_2)$
tend to 0 when N tends to
![]() $+\infty$
. Consequently, it is enough to prove that for N large enough, if
$+\infty$
. Consequently, it is enough to prove that for N large enough, if
![]() $\big(\mathcal{B}_1^{-}\big)^c$
and
$\big(\mathcal{B}_1^{-}\big)^c$
and
![]() $(\mathcal{B}_2)^c$
occur, if
$(\mathcal{B}_2)^c$
occur, if
![]() ${\tilde{I}}^{-}-I^{-} < N^{1/4}$
, and if
${\tilde{I}}^{-}-I^{-} < N^{1/4}$
, and if
![]() $I^{-} > -2(|x|+\theta)N$
, then
$I^{-} > -2(|x|+\theta)N$
, then
![]() $\big(\mathcal{B}_4^{-}\big)^c$
occurs. We assume
$\big(\mathcal{B}_4^{-}\big)^c$
occurs. We assume
![]() $\big(\mathcal{B}_1^{-}\big)^c$
,
$\big(\mathcal{B}_1^{-}\big)^c$
,
![]() $(\mathcal{B}_2)^c$
,
$(\mathcal{B}_2)^c$
,
![]() ${\tilde{I}}^{-}-I^{-} < N^{1/4}$
, and
${\tilde{I}}^{-}-I^{-} < N^{1/4}$
, and
![]() $I^{-} > -2(|x|+\theta)N$
. Since
$I^{-} > -2(|x|+\theta)N$
. Since
![]() $\big(\mathcal{B}_1^{-}\big)^c$
occurs and
$\big(\mathcal{B}_1^{-}\big)^c$
occurs and
![]() ${\tilde{I}}^{-} \geq I^{-} > -2(|x|+\theta)N$
, we get
${\tilde{I}}^{-} \geq I^{-} > -2(|x|+\theta)N$
, we get
![]() $\zeta_i=\eta_{j,-}(\ell^+(T_N,j))+1/2$
for any
$\zeta_i=\eta_{j,-}(\ell^+(T_N,j))+1/2$
for any
![]() $i\in\{{\tilde{I}}^{-}+1,\ldots,\chi(N)-1\}$
. Therefore, if
$i\in\{{\tilde{I}}^{-}+1,\ldots,\chi(N)-1\}$
. Therefore, if
![]() $i\in\{{\tilde{I}}^{-},\ldots,\chi(N)-1\}$
we get
$i\in\{{\tilde{I}}^{-},\ldots,\chi(N)-1\}$
we get
 \begin{equation*}\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{\chi(N)-1}\zeta_j=0,\end{equation*}
\begin{equation*}\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{\chi(N)-1}\zeta_j=0,\end{equation*}
and for
![]() $i \in \{I^{-},\ldots,{\tilde{I}}^{-}-1\}$
we have
$i \in \{I^{-},\ldots,{\tilde{I}}^{-}-1\}$
we have
 \begin{equation*} \left|\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{\chi(N)-1}\zeta_j\right| = \left|\sum_{j=i+1}^{{\tilde{I}}^{-}}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{{\tilde{I}}^{-}}\zeta_j\right| \end{equation*}
\begin{equation*} \left|\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{\chi(N)-1}\zeta_j\right| = \left|\sum_{j=i+1}^{{\tilde{I}}^{-}}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{{\tilde{I}}^{-}}\zeta_j\right| \end{equation*}
 \begin{equation*} \leq \sum_{j=i+1}^{{\tilde{I}}^{-}}\left(|\eta_{j,-}(\ell^+(T_N,j))+1/2|+|\zeta_j|\right) \leq 2({\tilde{I}}^{-} -I^{-})N^{1/16},\end{equation*}
\begin{equation*} \leq \sum_{j=i+1}^{{\tilde{I}}^{-}}\left(|\eta_{j,-}(\ell^+(T_N,j))+1/2|+|\zeta_j|\right) \leq 2({\tilde{I}}^{-} -I^{-})N^{1/16},\end{equation*}
since
![]() $\big(\mathcal{B}_2^{-}\big)^c$
occurs,
$\big(\mathcal{B}_2^{-}\big)^c$
occurs,
![]() $i+1 \geq I^{-} > -2(|x|+\theta)N$
, and by definition
$i+1 \geq I^{-} > -2(|x|+\theta)N$
, and by definition
![]() ${\tilde{I}}^{-} \leq \chi(N)-1 \leq 2(|x|+\theta)N$
. Moreover, we assumed
${\tilde{I}}^{-} \leq \chi(N)-1 \leq 2(|x|+\theta)N$
. Moreover, we assumed
![]() ${\tilde{I}}^{-}-I^{-} < N^{1/4}$
, which implies
${\tilde{I}}^{-}-I^{-} < N^{1/4}$
, which implies
 \begin{equation*}\left|\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{\chi(N)-1}\zeta_j \right| \leq 2 N^{1/4}N^{1/16}=2N^{5/16} < N^{1/3}\end{equation*}
\begin{equation*}\left|\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{\chi(N)-1}\zeta_j \right| \leq 2 N^{1/4}N^{1/16}=2N^{5/16} < N^{1/3}\end{equation*}
when N is large enough. Consequently, for any
![]() $i\in\{I^{-},\ldots,\chi(N)-1\}$
we have
$i\in\{I^{-},\ldots,\chi(N)-1\}$
we have
 \begin{equation*}\left|\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{\chi(N)-1}\zeta_j \right| < N^{1/3};\end{equation*}
\begin{equation*}\left|\sum_{j=i+1}^{\chi(N)-1}\big(\eta_{j,-}\big(\ell^+\big(T_N,j\big)\big)+1/2\big)-\sum_{j=i+1}^{\chi(N)-1}\zeta_j \right| < N^{1/3};\end{equation*}
therefore
![]() $\big(\mathcal{B}_4^{-}\big)^c$
occurs, which completes the proof.
$\big(\mathcal{B}_4^{-}\big)^c$
occurs, which completes the proof.
4. Skorokhod
 $M_1$
distance
$M_1$
distance
The goal of this section is to prove that when N is large,
![]() $Y_N^\pm$
is close in the Skorokhod
$Y_N^\pm$
is close in the Skorokhod
![]() $M_1$
distance to the function
$M_1$
distance to the function
![]() $Y_N$
defined as follows. For any N large enough, for
$Y_N$
defined as follows. For any N large enough, for
![]() $y\in\mathbb{R}$
, we set
$y\in\mathbb{R}$
, we set
 \begin{equation*}Y_N(y)=\frac{1}{\sqrt{N}}\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i\end{equation*}
\begin{equation*}Y_N(y)=\frac{1}{\sqrt{N}}\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i\end{equation*}
if
![]() $y \in \Big[{-}|x|-2\theta,\frac{\chi(N)}{N}\Big)$
,
$y \in \Big[{-}|x|-2\theta,\frac{\chi(N)}{N}\Big)$
,
 \begin{equation*}Y_N(y)=\frac{1}{\sqrt{N}}\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i\end{equation*}
\begin{equation*}Y_N(y)=\frac{1}{\sqrt{N}}\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i\end{equation*}
if
![]() $y \in \Big[\frac{\chi(N)}{N},|x|+2\theta\Big)$
, and
$y \in \Big[\frac{\chi(N)}{N},|x|+2\theta\Big)$
, and
![]() $Y_N(y)=0$
otherwise. We want to prove the following proposition.
$Y_N(y)=0$
otherwise. We want to prove the following proposition.
Proposition 5.
![]() $\mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y_N\big) > 3N^{-1/12}\big)$
tends to 0 when N tends to
$\mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y_N\big) > 3N^{-1/12}\big)$
tends to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
If we denote by
![]() $\mathcal{B}$
the event
$\mathcal{B}$
the event
 \begin{align*} & \mathcal{B}_1^{-} \cup \mathcal{B}_1^+ \cup \mathcal{B}_2 \cup \mathcal{B}_3^{-} \cup \mathcal{B}_3^+ \cup \mathcal{B}_4^{-} \cup \mathcal{B}_4^+ \cup \big\{|I^{-}+(|x|+2\theta)N| \geq N^{3/4}\big\}\\& \cup \big\{|I^+-(|x|+2\theta)N| \geq N^{3/4}\big\},\end{align*}
\begin{align*} & \mathcal{B}_1^{-} \cup \mathcal{B}_1^+ \cup \mathcal{B}_2 \cup \mathcal{B}_3^{-} \cup \mathcal{B}_3^+ \cup \mathcal{B}_4^{-} \cup \mathcal{B}_4^+ \cup \big\{|I^{-}+(|x|+2\theta)N| \geq N^{3/4}\big\}\\& \cup \big\{|I^+-(|x|+2\theta)N| \geq N^{3/4}\big\},\end{align*}
it will be enough to prove the following proposition.
Proposition 6.
When N is large enough, for all
![]() $a >0$
with
$a >0$
with
![]() $|(|x|+2\theta)-a|>N^{-1/8}$
, we have that
$|(|x|+2\theta)-a|>N^{-1/8}$
, we have that
![]() $\mathcal{B}^c \subset \big\{d_{M_1,a}\big(Y_N^\pm|_{[{-}a,a]},Y_N|_{[{-}a,a]}\big) \leq 2N^{-1/12}\big\}$
.
$\mathcal{B}^c \subset \big\{d_{M_1,a}\big(Y_N^\pm|_{[{-}a,a]},Y_N|_{[{-}a,a]}\big) \leq 2N^{-1/12}\big\}$
.
Proof
of Proposition 5 given Proposition 6. We assume Proposition 6 holds. Then, when N is large enough, if
![]() $\mathcal{B}^c$
occurs, for all
$\mathcal{B}^c$
occurs, for all
![]() $a >0$
with
$a >0$
with
![]() $|(|x|+2\theta)-a|>N^{-1/8}$
we have
$|(|x|+2\theta)-a|>N^{-1/8}$
we have
![]() $d_{M_1,a}\big(Y_N^\pm|_{[{-}a,a]},Y_N|_{[{-}a,a]}\big) \leq 2N^{-1/12}$
, which yields that
$d_{M_1,a}\big(Y_N^\pm|_{[{-}a,a]},Y_N|_{[{-}a,a]}\big) \leq 2N^{-1/12}$
, which yields that
 \begin{align*}d_{M_1}\big(Y_N^\pm,Y_N\big)&=\int_0^{+\infty}e^{-a}\big(d_{M_1,a}\big(Y_N^\pm|_{[{-}a,a]},Y_N|_{[{-}a,a]}\big) \wedge 1 \big)\mathrm{d}a \\&\leq \int_0^{+\infty}e^{-a}2N^{-1/12}\mathrm{d}a + 2 N^{-1/8}\\&= 2N^{-1/12}+ 2 N^{-1/8} \leq 3 N^{-1/12}.\end{align*}
\begin{align*}d_{M_1}\big(Y_N^\pm,Y_N\big)&=\int_0^{+\infty}e^{-a}\big(d_{M_1,a}\big(Y_N^\pm|_{[{-}a,a]},Y_N|_{[{-}a,a]}\big) \wedge 1 \big)\mathrm{d}a \\&\leq \int_0^{+\infty}e^{-a}2N^{-1/12}\mathrm{d}a + 2 N^{-1/8}\\&= 2N^{-1/12}+ 2 N^{-1/8} \leq 3 N^{-1/12}.\end{align*}
This implies that
![]() $\mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y_N\big) > 3 N^{-1/12}\big) \leq \mathbb{P}(\mathcal{B})$
when N is large enough. In addition,
$\mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y_N\big) > 3 N^{-1/12}\big) \leq \mathbb{P}(\mathcal{B})$
when N is large enough. In addition,
Applying Lemmas 2, 3, 5, 7, and 11 implies that
![]() $\mathbb{P}(\mathcal{B})$
tends to 0 when N tends to
$\mathbb{P}(\mathcal{B})$
tends to 0 when N tends to
![]() $+\infty$
; hence
$+\infty$
; hence
![]() $\mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y_N\big) > 3 N^{-1/12}\big)$
tends to 0 when N tends to
$\mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y_N\big) > 3 N^{-1/12}\big)$
tends to 0 when N tends to
![]() $+\infty$
, which is Proposition 5.
$+\infty$
, which is Proposition 5.
The remainder of this section is devoted to the proof of Proposition 6. The first thing we do is show that between
![]() $\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
and
$\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
and
![]() $\frac{((|x|+2\theta)N) \wedge I^+}{N}$
, the functions
$\frac{((|x|+2\theta)N) \wedge I^+}{N}$
, the functions
![]() $Y_N^\pm$
and
$Y_N^\pm$
and
![]() $Y_N$
are close in uniform distance, which is the following lemma.
$Y_N$
are close in uniform distance, which is the following lemma.
Lemma 12.
When N is large enough, if
![]() $(\mathcal{B}_2)^c$
,
$(\mathcal{B}_2)^c$
,
![]() $\big(\mathcal{B}_4^{-}\big)^c$
, and
$\big(\mathcal{B}_4^{-}\big)^c$
, and
![]() $\big(\mathcal{B}_4^+\big)^c$
occur, we have the following: if
$\big(\mathcal{B}_4^+\big)^c$
occur, we have the following: if
![]() $I^+ < (|x|+2\theta)N$
, then for any
$I^+ < (|x|+2\theta)N$
, then for any
we have
![]() $\big|Y_N^\pm(y)-Y_N(y)\big| \leq N^{-1/12}$
. If
$\big|Y_N^\pm(y)-Y_N(y)\big| \leq N^{-1/12}$
. If
![]() $I^+ \geq (|x|+2\theta)N$
, then we have
$I^+ \geq (|x|+2\theta)N$
, then we have
![]() $\big|Y_N^\pm(y)-Y_N(y)\big| \leq N^{-1/12}$
for
$\big|Y_N^\pm(y)-Y_N(y)\big| \leq N^{-1/12}$
for
![]() $y\in \left[\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{((|x|+2\theta)N) \wedge I^+}{N} \right)$
.
$y\in \left[\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{((|x|+2\theta)N) \wedge I^+}{N} \right)$
.
Proof
of Lemma 12. Writing down the proof is only a technical matter, as the meaning of
![]() $\big(\mathcal{B}_4^\pm\big)^c$
is that the local times are close to the process formed from the random variables of the coupling. The event
$\big(\mathcal{B}_4^\pm\big)^c$
is that the local times are close to the process formed from the random variables of the coupling. The event
![]() $(\mathcal{B}_2)^c$
is there to ensure that the difference terms that appear will be small. We spell out the proof only for
$(\mathcal{B}_2)^c$
is there to ensure that the difference terms that appear will be small. We spell out the proof only for
![]() $Y^{-}$
, as the proof for
$Y^{-}$
, as the proof for
![]() $Y^+$
is similar. We assume
$Y^+$
is similar. We assume
![]() $(\mathcal{B}_2)^c$
,
$(\mathcal{B}_2)^c$
,
![]() $\big(\mathcal{B}_4^{-}\big)^c$
, and
$\big(\mathcal{B}_4^{-}\big)^c$
, and
![]() $\big(\mathcal{B}_4^+\big)^c$
. Then if
$\big(\mathcal{B}_4^+\big)^c$
. Then if
![]() $\big($
if
$\big($
if
![]() $I^+\geq(|x|+2\theta)N$
we exclude the case
$I^+\geq(|x|+2\theta)N$
we exclude the case
![]() $y=\frac{((|x|+2\theta)N) \wedge I^+}{N}\big)$
, we have
$y=\frac{((|x|+2\theta)N) \wedge I^+}{N}\big)$
, we have
![]() $y \in \big[\frac{\chi(N)}{N},|x|+2\theta\big)$
, so
$y \in \big[\frac{\chi(N)}{N},|x|+2\theta\big)$
, so
 \begin{equation*}\big|Y_N^{-}(y)-Y_N(y)\big| = \frac{1}{\sqrt{N}}\bigg|\ell^{-}\big(T_N,\lfloor N y\rfloor\big)-N\left(\frac{|x|-|y|}{2}+\theta\right)_+-\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i\bigg|;\end{equation*}
\begin{equation*}\big|Y_N^{-}(y)-Y_N(y)\big| = \frac{1}{\sqrt{N}}\bigg|\ell^{-}\big(T_N,\lfloor N y\rfloor\big)-N\left(\frac{|x|-|y|}{2}+\theta\right)_+-\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i\bigg|;\end{equation*}
thus by (1) we obtain that
![]() $\big|Y_N^{-}(y)-Y_N(y)\big|$
is equal to
$\big|Y_N^{-}(y)-Y_N(y)\big|$
is equal to
 \begin{equation*} \frac{1}{\sqrt{N}}\left|\lfloor N \theta\rfloor-\mathbb{1}_{\{\iota=+\}}+\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)-N\left(\frac{|x|-|y|}{2}+\theta\right)_+-\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i\right| \end{equation*}
\begin{equation*} \frac{1}{\sqrt{N}}\left|\lfloor N \theta\rfloor-\mathbb{1}_{\{\iota=+\}}+\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)-N\left(\frac{|x|-|y|}{2}+\theta\right)_+-\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i\right| \end{equation*}
 \begin{equation*} \leq \frac{1}{\sqrt{N}}\left|\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)+\frac{\lfloor N y\rfloor-\chi(N)}{2}-\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i\right|+\frac{3}{\sqrt{N}} \end{equation*}
\begin{equation*} \leq \frac{1}{\sqrt{N}}\left|\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)+\frac{\lfloor N y\rfloor-\chi(N)}{2}-\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i\right|+\frac{3}{\sqrt{N}} \end{equation*}
 \begin{equation*} = \frac{1}{\sqrt{N}}\left|\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\big(\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)+1/2\big)-\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i\right|+\frac{3}{\sqrt{N}}. \end{equation*}
\begin{equation*} = \frac{1}{\sqrt{N}}\left|\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\big(\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)+1/2\big)-\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i\right|+\frac{3}{\sqrt{N}}. \end{equation*}
Now,
![]() $y \in \big[\frac{\chi(N)}{N},\frac{((|x|+2\theta)N) \wedge I^+}{N}\big]$
implies
$y \in \big[\frac{\chi(N)}{N},\frac{((|x|+2\theta)N) \wedge I^+}{N}\big]$
implies
![]() $\lfloor N y\rfloor \in \{\chi(N),\ldots,I^+\}$
; thus
$\lfloor N y\rfloor \in \{\chi(N),\ldots,I^+\}$
; thus
![]() $\big(\mathcal{B}_4^+\big)^c$
yields
$\big(\mathcal{B}_4^+\big)^c$
yields
![]() $\big|Y_N^{-}(y)-Y_N(y)\big| \leq \frac{1}{\sqrt{N}}N^{1/3}+\frac{3}{\sqrt{N}} \leq N^{-1/12}$
when N is large enough. We now consider the case
$\big|Y_N^{-}(y)-Y_N(y)\big| \leq \frac{1}{\sqrt{N}}N^{1/3}+\frac{3}{\sqrt{N}} \leq N^{-1/12}$
when N is large enough. We now consider the case
![]() $y \in \big[\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{\chi(N)}{N}\big)$
. Then
$y \in \big[\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{\chi(N)}{N}\big)$
. Then
![]() $y \in \big[{-}|x|-2\theta,\frac{\chi(N)}{N}\big)$
, and hence
$y \in \big[{-}|x|-2\theta,\frac{\chi(N)}{N}\big)$
, and hence
 \begin{equation*}\big|Y_N^{-}(y)-Y_N(y)\big| = \frac{1}{\sqrt{N}} \left|\ell^{-}\big(T_N,\lfloor N y\rfloor\big)-N\bigg(\frac{|x|-|y|}{2}+\theta\bigg)_+ -\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i \right|.\end{equation*}
\begin{equation*}\big|Y_N^{-}(y)-Y_N(y)\big| = \frac{1}{\sqrt{N}} \left|\ell^{-}\big(T_N,\lfloor N y\rfloor\big)-N\bigg(\frac{|x|-|y|}{2}+\theta\bigg)_+ -\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i \right|.\end{equation*}
Now, (2) yields
![]() $|\ell^{-}\big(T_N,\lfloor N y\rfloor\big)-\ell^+\big(T_N,\lfloor N y\rfloor\big)|=|\eta_{\lfloor N y\rfloor,-}\big(\ell^+\big(T_N,\lfloor N y\rfloor\big)\big)|$
, which is smaller than
$|\ell^{-}\big(T_N,\lfloor N y\rfloor\big)-\ell^+\big(T_N,\lfloor N y\rfloor\big)|=|\eta_{\lfloor N y\rfloor,-}\big(\ell^+\big(T_N,\lfloor N y\rfloor\big)\big)|$
, which is smaller than
![]() $N^{1/16}+1/2$
thanks to
$N^{1/16}+1/2$
thanks to
![]() $(\mathcal{B}_2)^c$
. We deduce that
$(\mathcal{B}_2)^c$
. We deduce that
 \begin{equation*}\big|Y_N^{-}(y)-Y_N(y)\big| \leq \frac{1}{\sqrt{N}}\left|\ell^+\big(T_N,\lfloor N y\rfloor\big)-N\bigg(\frac{|x|-|y|}{2}+\theta\bigg)_+ -\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i \right|+\frac{N^{1/16}+1/2}{\sqrt{N}};\end{equation*}
\begin{equation*}\big|Y_N^{-}(y)-Y_N(y)\big| \leq \frac{1}{\sqrt{N}}\left|\ell^+\big(T_N,\lfloor N y\rfloor\big)-N\bigg(\frac{|x|-|y|}{2}+\theta\bigg)_+ -\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i \right|+\frac{N^{1/16}+1/2}{\sqrt{N}};\end{equation*}
thus (1) implies that
![]() $\big|Y_N^{-}(y)-Y_N(y)\big|$
is smaller than
$\big|Y_N^{-}(y)-Y_N(y)\big|$
is smaller than
 \begin{equation*} \frac{1}{\sqrt{N}}\left|\lfloor N \theta\rfloor+\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\big(\eta_{i,-}\big(\ell^+\big(T_N,i\big)\big)+\mathbb{1}_{\{i > 0\}}\big)\qquad\qquad\qquad\qquad\qquad\qquad\quad\right. \end{equation*}
\begin{equation*} \frac{1}{\sqrt{N}}\left|\lfloor N \theta\rfloor+\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\big(\eta_{i,-}\big(\ell^+\big(T_N,i\big)\big)+\mathbb{1}_{\{i > 0\}}\big)\qquad\qquad\qquad\qquad\qquad\qquad\quad\right. \end{equation*}
 \begin{equation*} \qquad\qquad\qquad\qquad\qquad\qquad\left.-N\bigg(\frac{|x|-|y|}{2}+\theta\bigg)_+-\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i\right|+\frac{N^{1/16}+1/2}{\sqrt{N}} \end{equation*}
\begin{equation*} \qquad\qquad\qquad\qquad\qquad\qquad\left.-N\bigg(\frac{|x|-|y|}{2}+\theta\bigg)_+-\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i\right|+\frac{N^{1/16}+1/2}{\sqrt{N}} \end{equation*}
 \begin{equation*} \leq \frac{1}{\sqrt{N}}\left|\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\big(\eta_{i,-}\big(\ell^+\big(T_N,i\big)\big)+\mathbb{1}_{\{i > 0\}}\big)+\frac{\lfloor N y\rfloor+1-\chi(N)}{2}-\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i\right|+\frac{N^{1/16}+3}{\sqrt{N}} \end{equation*}
\begin{equation*} \leq \frac{1}{\sqrt{N}}\left|\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\big(\eta_{i,-}\big(\ell^+\big(T_N,i\big)\big)+\mathbb{1}_{\{i > 0\}}\big)+\frac{\lfloor N y\rfloor+1-\chi(N)}{2}-\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i\right|+\frac{N^{1/16}+3}{\sqrt{N}} \end{equation*}
 \begin{equation*} \leq \frac{1}{\sqrt{N}}\left|\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\big(\eta_{i,-}\big(\ell^+\big(T_N,i\big)\big)+1/2\big)-\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i\right|+\frac{N^{1/16}+3}{\sqrt{N}}. \end{equation*}
\begin{equation*} \leq \frac{1}{\sqrt{N}}\left|\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\big(\eta_{i,-}\big(\ell^+\big(T_N,i\big)\big)+1/2\big)-\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i\right|+\frac{N^{1/16}+3}{\sqrt{N}}. \end{equation*}
Furthermore,
![]() $y \in \Big[\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{\chi(N)}{N}\Big)$
implies
$y \in \Big[\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{\chi(N)}{N}\Big)$
implies
![]() $\lfloor N y\rfloor \in \{I^{-},\ldots,\chi(N)-1\}$
; hence
$\lfloor N y\rfloor \in \{I^{-},\ldots,\chi(N)-1\}$
; hence
![]() $\big(\mathcal{B}_4^{-}\big)^c$
yields
$\big(\mathcal{B}_4^{-}\big)^c$
yields
when N is large enough. Consequently, for any
![]() $y\in\big[\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{((|x|+2\theta)N) \wedge I^+}{N}\big]$
we have
$y\in\big[\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{((|x|+2\theta)N) \wedge I^+}{N}\big]$
we have
![]() $\big|Y_N^{-}(y)-Y_N(y)\big| \leq N^{-1/12}$
, which completes the proof of Lemma 12.
$\big|Y_N^{-}(y)-Y_N(y)\big| \leq N^{-1/12}$
, which completes the proof of Lemma 12.
We now prove Proposition 6. Let
![]() $a>0$
be such that
$a>0$
be such that
![]() $|(|x|+2\theta)-a|>N^{-1/8}$
. We will prove that when N is large enough,
$|(|x|+2\theta)-a|>N^{-1/8}$
. We will prove that when N is large enough,
![]() $\mathcal{B}^c \subset \big\{d_{M_1,a}\big(Y_N^\pm|_{[{-}a,a]},Y_N|_{[{-}a,a]}\big) \leq 2N^{-1/12}\big\}$
, and the threshold for N given by the proof will not depend on the value of a. There will be two cases depending on whether a is smaller than
$\mathcal{B}^c \subset \big\{d_{M_1,a}\big(Y_N^\pm|_{[{-}a,a]},Y_N|_{[{-}a,a]}\big) \leq 2N^{-1/12}\big\}$
, and the threshold for N given by the proof will not depend on the value of a. There will be two cases depending on whether a is smaller than
![]() $|x|+2\theta$
or not.
$|x|+2\theta$
or not.
4.1. Case a ∈ (0, |x| + 2θ − N−1/8)
This is the easier case. Indeed, the interval
![]() $[{-}a,a]$
will then be contained in
$[{-}a,a]$
will then be contained in
![]() $\Big[\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{((|x|+2\theta)N) \wedge I^+}{N}\Big)$
, inside which
$\Big[\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{((|x|+2\theta)N) \wedge I^+}{N}\Big)$
, inside which
![]() $Y_N^\pm$
and
$Y_N^\pm$
and
![]() $Y_N$
are close for the uniform norm by Lemma 12. We may then define parametric representations
$Y_N$
are close for the uniform norm by Lemma 12. We may then define parametric representations
![]() $\big(u_N^\pm,r_N^\pm\big)$
and
$\big(u_N^\pm,r_N^\pm\big)$
and
![]() $(u_N,r_N)$
of
$(u_N,r_N)$
of
![]() $Y_N^{-}|_{[{-}a,a]}$
and
$Y_N^{-}|_{[{-}a,a]}$
and
![]() $Y_N|_{[{-}a,a]}$
‘following the graphs of
$Y_N|_{[{-}a,a]}$
‘following the graphs of
![]() $Y_N^\pm|_{[{-}a,a]}$
and
$Y_N^\pm|_{[{-}a,a]}$
and
![]() $Y_N|_{[{-}a,a]}$
together’ so that
$Y_N|_{[{-}a,a]}$
together’ so that
![]() $u_N^\pm(t)=u_N(t)$
for all
$u_N^\pm(t)=u_N(t)$
for all
![]() $t\in[0,1]$
, and
$t\in[0,1]$
, and
(an explicit construction of these representations can be found in the first arXiv version of this paper [Reference Marêché5]). We deduce that
Moreover, if
![]() $\mathcal{B}^c$
occurs, since
$\mathcal{B}^c$
occurs, since
![]() $a\in\big(0,|x|+2\theta-N^{-1/8}\big)$
, for any
$a\in\big(0,|x|+2\theta-N^{-1/8}\big)$
, for any
![]() $y \in [{-}a,a]$
we have
$y \in [{-}a,a]$
we have
![]() $y \in \big({-}|x|-2\theta+N^{-1/8},|x|+2\theta-N^{-1/8}\big)$
; thus
$y \in \big({-}|x|-2\theta+N^{-1/8},|x|+2\theta-N^{-1/8}\big)$
; thus
![]() $-(|x|+2\theta)N+N^{3/4} \leq N y \leq (|x|+2\theta)N-N^{3/4}$
, which implies
$-(|x|+2\theta)N+N^{3/4} \leq N y \leq (|x|+2\theta)N-N^{3/4}$
, which implies
![]() $I^{-} < N y < I^+$
, and hence
$I^{-} < N y < I^+$
, and hence
![]() $y\in\big(\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{((|x|+2\theta)N) \wedge I^+}{N}\big)$
. So by Lemma 12 we have
$y\in\big(\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N},\frac{((|x|+2\theta)N) \wedge I^+}{N}\big)$
. So by Lemma 12 we have
![]() $\big|Y_N^\pm(y)-Y_N(y)\big| \leq N^{-1/12}$
. Consequently, if
$\big|Y_N^\pm(y)-Y_N(y)\big| \leq N^{-1/12}$
. Consequently, if
![]() $\mathcal{B}^c$
occurs, then
$\mathcal{B}^c$
occurs, then
![]() $d_{M_1,a}\big(Y_N^\pm|_{[{-}a,a]},Y_N|_{[{-}a,a]}\big) \leq N^{-1/12}$
.
$d_{M_1,a}\big(Y_N^\pm|_{[{-}a,a]},Y_N|_{[{-}a,a]}\big) \leq N^{-1/12}$
.
4.2. Case a > |x| + 2θ + N−1/8
This is the harder case, as we have to deal with what happens around
![]() $|x|+2\theta$
and
$|x|+2\theta$
and
![]() $-|x|-2\theta$
. We write down only the proof for
$-|x|-2\theta$
. We write down only the proof for
![]() $Y_N^{-}$
, since the proof for
$Y_N^{-}$
, since the proof for
![]() $Y_N^+$
is similar (one may remember that (2) allows us to bound the
$Y_N^+$
is similar (one may remember that (2) allows us to bound the
![]() $\ell^{-}(T_N,i)-\ell^+(T_N,i)$
when
$\ell^{-}(T_N,i)-\ell^+(T_N,i)$
when
![]() $(\mathcal{B}_2)^c$
occurs, and hence when
$(\mathcal{B}_2)^c$
occurs, and hence when
![]() $\mathcal{B}^c$
occurs). Once again, we will define parametric representations
$\mathcal{B}^c$
occurs). Once again, we will define parametric representations
![]() $\big(u_N^{-},r_N^{-}\big)$
and
$\big(u_N^{-},r_N^{-}\big)$
and
![]() $(u_N,r_N)$
of
$(u_N,r_N)$
of
![]() $Y_N^{-}|_{[{-}a,a]}$
and
$Y_N^{-}|_{[{-}a,a]}$
and
![]() $Y_N|_{[{-}a,a]}$
. The definition will depend on whether
$Y_N|_{[{-}a,a]}$
. The definition will depend on whether
![]() $I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
or not, and also on whether
$I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
or not, and also on whether
![]() $I^{-} \geq -\lfloor(|x|+2\theta)N\rfloor$
or not. We explain it for abscissas in [0,a] depending on whether
$I^{-} \geq -\lfloor(|x|+2\theta)N\rfloor$
or not. We explain it for abscissas in [0,a] depending on whether
![]() $I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
or not; the constructions for abscissas in
$I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
or not; the constructions for abscissas in
![]() $[{-}a,0]$
are similar, depending on whether
$[{-}a,0]$
are similar, depending on whether
![]() $I^{-} \geq -\lfloor(|x|+2\theta)N\rfloor$
or not.
$I^{-} \geq -\lfloor(|x|+2\theta)N\rfloor$
or not.
We first assume
![]() $I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
. Between 0 and
$I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
. Between 0 and
![]() $\frac{I^+}{N}$
, as in the case
$\frac{I^+}{N}$
, as in the case
![]() $a\in(0,|x|+2\theta-N^{-1/8})$
, the parametric representations will follow the completed graphs of
$a\in(0,|x|+2\theta-N^{-1/8})$
, the parametric representations will follow the completed graphs of
![]() $Y_N^{-}$
and
$Y_N^{-}$
and
![]() $Y_N$
in parallel (see Figure 1(a)). The next step, once
$Y_N$
in parallel (see Figure 1(a)). The next step, once
![]() $\big(u_N^{-},r_N^{-}\big)$
has reached
$\big(u_N^{-},r_N^{-}\big)$
has reached
![]() $\left(\frac{I^+}{N},Y_N^{-}\left(\frac{I^+}{N} \right)\right)$
, is to freeze it there while
$\left(\frac{I^+}{N},Y_N^{-}\left(\frac{I^+}{N} \right)\right)$
, is to freeze it there while
![]() $(u_N,r_N)$
follows the graph of
$(u_N,r_N)$
follows the graph of
![]() $Y_N$
from
$Y_N$
from
![]() $\left(\frac{I^+}{N},Y_N\left(\frac{I^+}{N} \right)\right)$
to
$\left(\frac{I^+}{N},Y_N\left(\frac{I^+}{N} \right)\right)$
to
![]() $(|x|+2\theta,Y_N((|x|+2\theta))^{-})$
(see Figure 1(b)). For
$(|x|+2\theta,Y_N((|x|+2\theta))^{-})$
(see Figure 1(b)). For
![]() $y \geq \frac{I^+}{N}$
we have
$y \geq \frac{I^+}{N}$
we have
![]() $\ell^{-}\big(T_N,\lfloor N y\rfloor\big)=0$
(see Lemma 6); thus
$\ell^{-}\big(T_N,\lfloor N y\rfloor\big)=0$
(see Lemma 6); thus
![]() $Y_N(y)=-N\Big(\frac{|x|-|y|}{2}+\theta\Big)_+$
, and hence
$Y_N(y)=-N\Big(\frac{|x|-|y|}{2}+\theta\Big)_+$
, and hence
![]() $Y_N^{-}\,:\,[\frac{I^+}{N},|x|+2\theta] \mapsto \mathbb{R}$
is affine. Therefore, the following step is to simultaneously move
$Y_N^{-}\,:\,[\frac{I^+}{N},|x|+2\theta] \mapsto \mathbb{R}$
is affine. Therefore, the following step is to simultaneously move
![]() $\big(u_N^{-},r_N^{-}\big)$
from
$\big(u_N^{-},r_N^{-}\big)$
from
![]() $\left(\frac{I^+}{N},Y_N^{-}\left(\frac{I^+}{N} \right)\right)$
to
$\left(\frac{I^+}{N},Y_N^{-}\left(\frac{I^+}{N} \right)\right)$
to
![]() $(|x|+2\theta,Y_N^{-}(|x|+2\theta))=(|x|+2\theta,0)$
and
$(|x|+2\theta,Y_N^{-}(|x|+2\theta))=(|x|+2\theta,0)$
and
![]() $(u_N,r_N)$
from
$(u_N,r_N)$
from
![]() $(|x|+2\theta,Y_N((|x|+2\theta)^{-}))$
to
$(|x|+2\theta,Y_N((|x|+2\theta)^{-}))$
to
![]() $(|x|+2\theta,0)$
(see Figure 1(c)); here the two parametric representations will remain close. After this step, both parametric representations are at
$(|x|+2\theta,0)$
(see Figure 1(c)); here the two parametric representations will remain close. After this step, both parametric representations are at
![]() $(|x|+2\theta,0)$
, and they will go together to (a,0) (see Figure 1(d)).
$(|x|+2\theta,0)$
, and they will go together to (a,0) (see Figure 1(d)).

Figure 1. The successive steps of the parametric representations of
![]() $Y_N^{-}|_{[{-}a,a]}$
and
$Y_N^{-}|_{[{-}a,a]}$
and
![]() $Y_N|_{[{-}a,a]}$
if
$Y_N|_{[{-}a,a]}$
if
![]() $I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
. At each step, the parts of the graphs through which the parametric representations travel are thickened.
$I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
. At each step, the parts of the graphs through which the parametric representations travel are thickened.
We now assume
![]() $I^+ > \lfloor(|x|+2\theta)N\rfloor$
. We also assume
$I^+ > \lfloor(|x|+2\theta)N\rfloor$
. We also assume
![]() $\frac{I^+}{N} \leq a$
$\frac{I^+}{N} \leq a$
![]() $\big($
if
$\big($
if
![]() $\frac{I^+}{N} > a$
, we may choose anything for
$\frac{I^+}{N} > a$
, we may choose anything for
![]() $\big(u_N^{-},r_N^{-}\big)$
,
$\big(u_N^{-},r_N^{-}\big)$
,
![]() $(u_N,r_N)$
; this will not happen if
$(u_N,r_N)$
; this will not happen if
![]() $\mathcal{B}^c$
occurs
$\mathcal{B}^c$
occurs
![]() $\big)$
. Between 0 and
$\big)$
. Between 0 and
![]() $|x|+2\theta$
, the parametric representations will follow the completed graphs of
$|x|+2\theta$
, the parametric representations will follow the completed graphs of
![]() $Y_N^{-}$
and
$Y_N^{-}$
and
![]() $Y_N$
in parallel (see Figure 2(a)). Once the abscissa
$Y_N$
in parallel (see Figure 2(a)). Once the abscissa
![]() $|x|+2\theta$
is reached, the next step is to move
$|x|+2\theta$
is reached, the next step is to move
![]() $\big(u_N^{-},r_N^{-}\big)$
from
$\big(u_N^{-},r_N^{-}\big)$
from
![]() $(|x|+2\theta,Y_N^{-}(|x|+2\theta))$
to
$(|x|+2\theta,Y_N^{-}(|x|+2\theta))$
to
![]() $\left(\frac{I^+}{N},Y_N^{-}\left(\frac{I^+}{N} \right)\right)$
, which is
$\left(\frac{I^+}{N},Y_N^{-}\left(\frac{I^+}{N} \right)\right)$
, which is
![]() $\big(\frac{I^+}{N},0\big)$
, and at the same time to move
$\big(\frac{I^+}{N},0\big)$
, and at the same time to move
![]() $(u_N,r_N)$
from
$(u_N,r_N)$
from
![]() $(|x|+2\theta,Y_N(|x|+2\theta))$
to
$(|x|+2\theta,Y_N(|x|+2\theta))$
to
![]() $(|x|+2\theta,0)$
(see Figure 2(b)). We will prove the two representations are close by controlling the local times. At the next step we freeze
$(|x|+2\theta,0)$
(see Figure 2(b)). We will prove the two representations are close by controlling the local times. At the next step we freeze
![]() $\big(u_N^{-},r_N^{-}\big)$
at
$\big(u_N^{-},r_N^{-}\big)$
at
![]() $\big(\frac{I^+}{N},0\big)$
while
$\big(\frac{I^+}{N},0\big)$
while
![]() $(u_N,r_N)$
goes from
$(u_N,r_N)$
goes from
![]() $(|x|+2\theta,0)$
to
$(|x|+2\theta,0)$
to
![]() $\big(\frac{I^+}{N},0\big)$
(see Figure 2(c)). After this step, both parametric representations are at
$\big(\frac{I^+}{N},0\big)$
(see Figure 2(c)). After this step, both parametric representations are at
![]() $\big(\frac{I^+}{N},0\big)$
, and they will go together from
$\big(\frac{I^+}{N},0\big)$
, and they will go together from
![]() $\big(\frac{I^+}{N},0\big)$
to (a,0) (see Figure 2(d)). Again, a more rigorous definition of the parametric representations is available in the first arXiv version of this paper [Reference Marêché5].
$\big(\frac{I^+}{N},0\big)$
to (a,0) (see Figure 2(d)). Again, a more rigorous definition of the parametric representations is available in the first arXiv version of this paper [Reference Marêché5].

Figure 2. The successive steps of the parametric representations of
![]() $Y_N^{-}|_{[{-}a,a]}$
and
$Y_N^{-}|_{[{-}a,a]}$
and
![]() $Y_N|_{[{-}a,a]}$
if
$Y_N|_{[{-}a,a]}$
if
![]() $I^+ > \lfloor(|x|+2\theta)N\rfloor$
. At each step, the parts of the graphs through which the parametric representations travel are thickened.
$I^+ > \lfloor(|x|+2\theta)N\rfloor$
. At each step, the parts of the graphs through which the parametric representations travel are thickened.
We can now bound the Skorokhod
![]() $M_1$
distance between
$M_1$
distance between
![]() $Y_N^{-}|_{[{-}a,a]}$
and
$Y_N^{-}|_{[{-}a,a]}$
and
![]() $Y_N|_{[{-}a,a]}$
. From its definition, we have
$Y_N|_{[{-}a,a]}$
. From its definition, we have
hence we only have to prove that
![]() $\mathcal{B}^c \subset \{\max\big(\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty\big) \leq 2N^{-1/12}\}$
when N is large enough. We are going to break down
$\mathcal{B}^c \subset \{\max\big(\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty\big) \leq 2N^{-1/12}\}$
when N is large enough. We are going to break down
![]() $\Big\{\max\big(\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty\big) \leq 2N^{-1/12}\Big\}$
into three events. We may write
$\Big\{\max\big(\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty\big) \leq 2N^{-1/12}\Big\}$
into three events. We may write
Consequently, to prove that
![]() $\mathcal{B}^c \subset \big\{\max\big(\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty\big) \leq 2N^{-1/12}\big\}$
when N is large enough and thus complete the proof of Proposition 6, we only have to prove the following lemmas.
$\mathcal{B}^c \subset \big\{\max\big(\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty\big) \leq 2N^{-1/12}\big\}$
when N is large enough and thus complete the proof of Proposition 6, we only have to prove the following lemmas.
Lemma 13.
We have
![]() $\mathcal{B}^c \subset \Big\{$
between
$\mathcal{B}^c \subset \Big\{$
between
![]() $\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
and
$\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
and
![]() $\frac{((|x|+2\theta)N) \wedge I^+}{N},\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\Big\}$
when N is large enough.
$\frac{((|x|+2\theta)N) \wedge I^+}{N},\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\Big\}$
when N is large enough.
Lemma 14.
We have
![]() $\mathcal{B}^c \cap \{I^+ \leq \lfloor(|x|+2\theta)N\rfloor\} \subset \Big\{$
between
$\mathcal{B}^c \cap \{I^+ \leq \lfloor(|x|+2\theta)N\rfloor\} \subset \Big\{$
between
![]() $\frac{((|x|+2\theta)N) \wedge I^+}{N}$
and a,
$\frac{((|x|+2\theta)N) \wedge I^+}{N}$
and a,
![]() $\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\Big\}$
and
$\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\Big\}$
and
![]() $\mathcal{B}^c \cap \{I^{-} \geq -\lfloor(|x|+2\theta)N\rfloor\} \subset \big\{$
between
$\mathcal{B}^c \cap \{I^{-} \geq -\lfloor(|x|+2\theta)N\rfloor\} \subset \big\{$
between
![]() $-a$
and
$-a$
and
![]() $\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
,
$\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
,
![]() $\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\big\}\big)$
when N is large enough.
$\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\big\}\big)$
when N is large enough.
Lemma 15.
We have
![]() $\mathcal{B}^c \cap \{I^+ > \lfloor(|x|+2\theta)N\rfloor\} \subset \Big\{$
between
$\mathcal{B}^c \cap \{I^+ > \lfloor(|x|+2\theta)N\rfloor\} \subset \Big\{$
between
![]() $\frac{((|x|+2\theta)N) \wedge I^+}{N}$
and a,
$\frac{((|x|+2\theta)N) \wedge I^+}{N}$
and a,
![]() $\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\Big\}$
and
$\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\Big\}$
and
![]() $\mathcal{B}^c \cap \{I^{-} < -\lfloor(|x|+2\theta)N\rfloor\} \subset \big\{$
between
$\mathcal{B}^c \cap \{I^{-} < -\lfloor(|x|+2\theta)N\rfloor\} \subset \big\{$
between
![]() $-a$
and
$-a$
and
![]() $\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
,
$\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
,
![]() $\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\big\}\big)$
when N is large enough.
$\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\big\}\big)$
when N is large enough.
We now prove Lemmas 13, 14, and 15.
Proof
of Lemma 13. We assume
![]() $\mathcal{B}^c$
occurs. In the part of the parametric representations between
$\mathcal{B}^c$
occurs. In the part of the parametric representations between
![]() $\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
and
$\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
and
![]() $\frac{((|x|+2\theta)N) \wedge I^+}{N}$
, corresponding to Figures 1(a) and 2(a), we follow the completed graphs of
$\frac{((|x|+2\theta)N) \wedge I^+}{N}$
, corresponding to Figures 1(a) and 2(a), we follow the completed graphs of
![]() $Y_N^{-}$
and
$Y_N^{-}$
and
![]() $Y_N$
in parallel. Therefore
$Y_N$
in parallel. Therefore
![]() $u_N^{-}(t)=u_N(t)$
and
$u_N^{-}(t)=u_N(t)$
and
If
![]() $(|x|+2\theta)N$
is not an integer or
$(|x|+2\theta)N$
is not an integer or
![]() $I^+<(|x|+2\theta)N$
, then by Lemma 12, this is smaller than
$I^+<(|x|+2\theta)N$
, then by Lemma 12, this is smaller than
![]() $N^{-12}$
when N is large enough, and we are done. If
$N^{-12}$
when N is large enough, and we are done. If
![]() $(|x|+2\theta)N$
is an integer and
$(|x|+2\theta)N$
is an integer and
![]() $I^+\geq(|x|+2\theta)N$
, there is a small complication, since the parametric representations follow the graph of
$I^+\geq(|x|+2\theta)N$
, there is a small complication, since the parametric representations follow the graph of
![]() $Y_N$
until
$Y_N$
until
![]() $Y_N((|x|+2\theta)^{-})$
, but should follow the graph of
$Y_N((|x|+2\theta)^{-})$
, but should follow the graph of
![]() $Y_N^{-}$
until
$Y_N^{-}$
until
![]() $Y_N^{-}(|x|+2\theta)$
. The solution is to freeze the representation of
$Y_N^{-}(|x|+2\theta)$
. The solution is to freeze the representation of
![]() $Y_N$
at
$Y_N$
at
![]() $Y_N((|x|+2\theta)^{-})$
while that of
$Y_N((|x|+2\theta)^{-})$
while that of
![]() $Y_N^{-}$
goes from
$Y_N^{-}$
goes from
![]() $Y_N^{-}((|x|+2\theta)^{-})$
to
$Y_N^{-}((|x|+2\theta)^{-})$
to
![]() $Y_N^{-}(|x|+2\theta)$
. Then, between
$Y_N^{-}(|x|+2\theta)$
. Then, between
![]() $\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
and
$\frac{({-}(|x|+2\theta)N) \vee I^{-}}{N}$
and
![]() $(|x|+2\theta)^{-}$
, we have
$(|x|+2\theta)^{-}$
, we have
by Lemma 12 when N is large enough. Furthermore, when going from
![]() $Y_N^{-}((|x|+2\theta)^{-})$
to
$Y_N^{-}((|x|+2\theta)^{-})$
to
![]() $Y_N^{-}(|x|+2\theta)$
, we have
$Y_N^{-}(|x|+2\theta)$
, we have
when N is large enough. In addition, when N is large enough, (1) yields
 \begin{align*}\big|Y_N^{-}(|x|+2\theta)-Y_N^{-}((|x|+2\theta)^{-})\big| &=\frac{1}{\sqrt{N}}\big|\ell^{-}\big(T_N,(|x|+2\theta)N\big)-\ell^{-}\big(T_N,(|x|+2\theta)N-1\big)\big|\\&=\frac{1}{\sqrt{N}}\big|\eta_{(|x|+2\theta)N-1,+}\big(\ell^{-}\big(T_N,(|x|+2\theta)N-1\big)\big)\big|\\&\leq \frac{N^{1/16}+1/2}{\sqrt{N}}\end{align*}
\begin{align*}\big|Y_N^{-}(|x|+2\theta)-Y_N^{-}((|x|+2\theta)^{-})\big| &=\frac{1}{\sqrt{N}}\big|\ell^{-}\big(T_N,(|x|+2\theta)N\big)-\ell^{-}\big(T_N,(|x|+2\theta)N-1\big)\big|\\&=\frac{1}{\sqrt{N}}\big|\eta_{(|x|+2\theta)N-1,+}\big(\ell^{-}\big(T_N,(|x|+2\theta)N-1\big)\big)\big|\\&\leq \frac{N^{1/16}+1/2}{\sqrt{N}}\end{align*}
since
![]() $(\mathcal{B}_2)^c$
occurs. This yields
$(\mathcal{B}_2)^c$
occurs. This yields
![]() $\big|r_N^{-}(t)-r_N(t)\big| \leq N^{-1/12}+\frac{N^{1/16}+1/2}{\sqrt{N}} \leq 2N^{-1/12}$
when N is large enough, which completes the proof.
$\big|r_N^{-}(t)-r_N(t)\big| \leq N^{-1/12}+\frac{N^{1/16}+1/2}{\sqrt{N}} \leq 2N^{-1/12}$
when N is large enough, which completes the proof.
Proof
of Lemma 14. This lemma deals with the ‘right part’ of the parametric representations in the case
![]() $I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
, and with the ‘left part’ in the case
$I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
, and with the ‘left part’ in the case
![]() $I^{-} \geq -\lfloor(|x|+2\theta)N\rfloor$
, corresponding to Panels (b), (c), and (d) of Figure 1. The idea of the argument is that in the step corresponding to Figure 1(b), the representation of
$I^{-} \geq -\lfloor(|x|+2\theta)N\rfloor$
, corresponding to Panels (b), (c), and (d) of Figure 1. The idea of the argument is that in the step corresponding to Figure 1(b), the representation of
![]() $Y_N$
does not move much horizontally, as
$Y_N$
does not move much horizontally, as
![]() $\frac{I^+}{N}$
is close to
$\frac{I^+}{N}$
is close to
![]() $|x|+2\theta$
by Lemma 7, so it does not have time to move too much vertically. In the step corresponding to Figure 1(c), the representations of
$|x|+2\theta$
by Lemma 7, so it does not have time to move too much vertically. In the step corresponding to Figure 1(c), the representations of
![]() $Y_N^{-}$
and
$Y_N^{-}$
and
![]() $Y_N$
will thus start from points that are close and go to the same point, which means they stay close to each other.
$Y_N$
will thus start from points that are close and go to the same point, which means they stay close to each other.
We now give the rigorous argument. We spell out the proof only for
![]() $\mathcal{B}^c \cap \{I^+ \leq \lfloor(|x|+2\theta)N\rfloor\}$
, as the other case is similar. Let us assume
$\mathcal{B}^c \cap \{I^+ \leq \lfloor(|x|+2\theta)N\rfloor\}$
, as the other case is similar. Let us assume
![]() $\mathcal{B}^c$
occurs and
$\mathcal{B}^c$
occurs and
![]() $I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
. Firstly, we notice that in the part of the parametric representations corresponding to Figure 1(d) we have
$I^+ \leq \lfloor(|x|+2\theta)N\rfloor$
. Firstly, we notice that in the part of the parametric representations corresponding to Figure 1(d) we have
![]() $\big(u_N^{-}(t),r_N^{-}(t)\big)=\big(u_N(t),r_N(t)\big)$
, so we consider only the parts corresponding to Figures 1(b) and 1(c). We first consider the case in which
$\big(u_N^{-}(t),r_N^{-}(t)\big)=\big(u_N(t),r_N(t)\big)$
, so we consider only the parts corresponding to Figures 1(b) and 1(c). We first consider the case in which
![]() $(|x|+2\theta)N$
is not an integer or
$(|x|+2\theta)N$
is not an integer or
![]() $I^+ < \lfloor(|x|+2\theta)N\rfloor$
. We begin by dealing with
$I^+ < \lfloor(|x|+2\theta)N\rfloor$
. We begin by dealing with
![]() $\big|u_N^{-}(t)-u_N(t)\big|$
. By the definition of our parametric representations,
$\big|u_N^{-}(t)-u_N(t)\big|$
. By the definition of our parametric representations,
![]() $\big|u_N^{-}(t)-u_N(t)\big| \leq ||x\big|+2\theta-\frac{I^+}{N}\big|$
. Furthermore,
$\big|u_N^{-}(t)-u_N(t)\big| \leq ||x\big|+2\theta-\frac{I^+}{N}\big|$
. Furthermore,
![]() $\mathcal{B}^c$
occurs; thus we have
$\mathcal{B}^c$
occurs; thus we have
![]() $|I^+-(|x|+2\theta)N| < N^{3/4}$
, and hence
$|I^+-(|x|+2\theta)N| < N^{3/4}$
, and hence
![]() $\big|u_N^{-}(t)-u_N(t)\big| \leq N^{-1/4}$
.
$\big|u_N^{-}(t)-u_N(t)\big| \leq N^{-1/4}$
.
We now deal with
![]() $\big|r_N^{-}(t)-r_N(t)\big|$
. Remembering the definition of our parametric representations, we notice that in the part corresponding to Figure 1(c),
$\big|r_N^{-}(t)-r_N(t)\big|$
. Remembering the definition of our parametric representations, we notice that in the part corresponding to Figure 1(c),
![]() $r_N^{-}$
and
$r_N^{-}$
and
![]() $r_N$
are affine functions, so the maximum value of
$r_N$
are affine functions, so the maximum value of
![]() $\big|r_N^{-}(t)-r_N(t)\big|$
on this part is reached either at the beginning or at the end of the part. Moreover, at the end of the part we have
$\big|r_N^{-}(t)-r_N(t)\big|$
on this part is reached either at the beginning or at the end of the part. Moreover, at the end of the part we have
![]() $r_N^{-}(t)=r_N(t)=0$
, so the maximum is reached at the beginning. Therefore, if
$r_N^{-}(t)=r_N(t)=0$
, so the maximum is reached at the beginning. Therefore, if
![]() $\big|r_N^{-}(t)-r_N(t)\big| \leq 2N^{-1/12}$
in the part corresponding to Figure 1(b), then
$\big|r_N^{-}(t)-r_N(t)\big| \leq 2N^{-1/12}$
in the part corresponding to Figure 1(b), then
![]() $\big|r_N^{-}(t)-r_N(t)\big| \leq 2N^{-1/12}$
in the part corresponding to Figure 1(c), and this completes the proof when
$\big|r_N^{-}(t)-r_N(t)\big| \leq 2N^{-1/12}$
in the part corresponding to Figure 1(c), and this completes the proof when
![]() $(|x|+2\theta)N$
is not an integer or
$(|x|+2\theta)N$
is not an integer or
![]() $I^+ < \lfloor(|x|+2\theta)N\rfloor$
.
$I^+ < \lfloor(|x|+2\theta)N\rfloor$
.
We thus have to study the part corresponding to Figure 1(b). By the definition of our parametric representations,
so it is enough to prove that when N is large enough,
![]() $\sup \left\{ \left|Y_N^{-}\left(\frac{I^+}{N} \right)-\right.\right.$
$\sup \left\{ \left|Y_N^{-}\left(\frac{I^+}{N} \right)-\right.\right.$
![]() $ \left.Y_N(y) \right|\,:\,y\in \left.\left[\frac{I^+}{N},|x|+2\theta \right) \right\} \leq 2N^{-1/12}$
. Moreover, for any
$ \left.Y_N(y) \right|\,:\,y\in \left.\left[\frac{I^+}{N},|x|+2\theta \right) \right\} \leq 2N^{-1/12}$
. Moreover, for any
![]() $y\in \left[\frac{I^+}{N},|x|+2\theta \right)$
, we have
$y\in \left[\frac{I^+}{N},|x|+2\theta \right)$
, we have
Since
![]() $\mathcal{B}^c$
occurs, we have that
$\mathcal{B}^c$
occurs, we have that
![]() $(\mathcal{B}_2)^c$
,
$(\mathcal{B}_2)^c$
,
![]() $\big(\mathcal{B}_4^{-}\big)^c$
, and
$\big(\mathcal{B}_4^{-}\big)^c$
, and
![]() $\big(\mathcal{B}_4^+\big)^c$
occur; hence Lemma 12 implies
$\big(\mathcal{B}_4^+\big)^c$
occur; hence Lemma 12 implies
![]() $\left|Y_N^{-}\left(\frac{I^+}{N} \right)-Y_N\left(\frac{I^+}{N} \right)\right| \leq N^{-1/12}$
when N is large enough, and so
$\left|Y_N^{-}\left(\frac{I^+}{N} \right)-Y_N\left(\frac{I^+}{N} \right)\right| \leq N^{-1/12}$
when N is large enough, and so
 \begin{equation*}\left|Y_N^{-} \left(\frac{I^+}{N} \right)-Y_N(y) \right| \leq \left|Y_N \left(\frac{I^+}{N} \right)-Y_N(y) \right|+N^{-1/12} \leq \frac{1}{\sqrt{N}} \left|\sum_{i=I^+}^{\lfloor Ny \rfloor-1}\zeta_i \right|+N^{-1/12}.\end{equation*}
\begin{equation*}\left|Y_N^{-} \left(\frac{I^+}{N} \right)-Y_N(y) \right| \leq \left|Y_N \left(\frac{I^+}{N} \right)-Y_N(y) \right|+N^{-1/12} \leq \frac{1}{\sqrt{N}} \left|\sum_{i=I^+}^{\lfloor Ny \rfloor-1}\zeta_i \right|+N^{-1/12}.\end{equation*}
We deduce that
 \begin{align*} \sup \!\left\{ \left|Y_N^{-}\left(\frac{I^+}{N} \right)-Y_N(y) \right|\,:\,y\in \left[\frac{I^+}{N},|x|+2\theta \right) \right\} & \leq \sup\!\left\{\frac{1}{\sqrt{N}} \left|\sum_{i=I^+}^{\lfloor Ny \rfloor-1}\zeta_i \right|:\,y\in \left[\frac{I^+}{N},|x|+2\theta \right)\!\right\}\\&\quad +N^{-1/12}.\end{align*}
\begin{align*} \sup \!\left\{ \left|Y_N^{-}\left(\frac{I^+}{N} \right)-Y_N(y) \right|\,:\,y\in \left[\frac{I^+}{N},|x|+2\theta \right) \right\} & \leq \sup\!\left\{\frac{1}{\sqrt{N}} \left|\sum_{i=I^+}^{\lfloor Ny \rfloor-1}\zeta_i \right|:\,y\in \left[\frac{I^+}{N},|x|+2\theta \right)\!\right\}\\&\quad +N^{-1/12}.\end{align*}
Furthermore,
![]() $\mathcal{B}^c$
occurs; hence
$\mathcal{B}^c$
occurs; hence
![]() $|I^+-(|x|+2\theta)N| < N^{3/4}$
, and thus
$|I^+-(|x|+2\theta)N| < N^{3/4}$
, and thus
 \begin{align*}&\sup \left\{ \left|Y_N^{-}\left(\frac{I^+}{N} \right)-Y_N(y) \right|:\,y\in \left[\frac{I^+}{N},|x|+2\theta \right) \right\} \\& \qquad \leq \frac{1}{\sqrt{N}}\max_{\lfloor(|x|+2\theta)N\rfloor-N^{3/4} \leq i_1 \leq i_2 \leq \lfloor (|x|+2\theta)N\rfloor}\frac{1}{\sqrt{N}}\left|\sum_{i=i_1}^{i_2}\zeta_i \right|+N^{-1/12}. \end{align*}
\begin{align*}&\sup \left\{ \left|Y_N^{-}\left(\frac{I^+}{N} \right)-Y_N(y) \right|:\,y\in \left[\frac{I^+}{N},|x|+2\theta \right) \right\} \\& \qquad \leq \frac{1}{\sqrt{N}}\max_{\lfloor(|x|+2\theta)N\rfloor-N^{3/4} \leq i_1 \leq i_2 \leq \lfloor (|x|+2\theta)N\rfloor}\frac{1}{\sqrt{N}}\left|\sum_{i=i_1}^{i_2}\zeta_i \right|+N^{-1/12}. \end{align*}
Since
![]() $\mathcal{B}^c$
occurs,
$\mathcal{B}^c$
occurs,
![]() $\big(\mathcal{B}_3^+\big)^c$
occurs; hence
$\big(\mathcal{B}_3^+\big)^c$
occurs; hence
 \begin{align*}&\sup \left\{ \left|Y_N^{-}\left(\frac{I^+}{N} \right)-Y_N(y) \right|\,:\,y\in \left[\frac{I^+}{N},|x|+2\theta \right) \right\} \\&\qquad \leq \frac{N^{19/48}}{\sqrt{N}}+N^{-1/12}=N^{-5/48}+N^{-1/12} \leq 2 N^{-1/12}, \end{align*}
\begin{align*}&\sup \left\{ \left|Y_N^{-}\left(\frac{I^+}{N} \right)-Y_N(y) \right|\,:\,y\in \left[\frac{I^+}{N},|x|+2\theta \right) \right\} \\&\qquad \leq \frac{N^{19/48}}{\sqrt{N}}+N^{-1/12}=N^{-5/48}+N^{-1/12} \leq 2 N^{-1/12}, \end{align*}
which is enough.
We now consider the case in which
![]() $(|x|+2\theta)N$
is an integer and
$(|x|+2\theta)N$
is an integer and
![]() $I^+ = \lfloor(|x|+2\theta)N\rfloor$
. Then the step corresponding to Figure 1(b) does not exist; we only have to deal with that of Figure 1(c), which comes mostly from Lemma 12, as this lemma ensures
$I^+ = \lfloor(|x|+2\theta)N\rfloor$
. Then the step corresponding to Figure 1(b) does not exist; we only have to deal with that of Figure 1(c), which comes mostly from Lemma 12, as this lemma ensures
![]() $Y_N^{-}((|x|+2\theta)^{-})$
and
$Y_N^{-}((|x|+2\theta)^{-})$
and
![]() $Y_N((|x|+2\theta)^{-})$
are close (we will actually prove they are both close to 0). Since
$Y_N((|x|+2\theta)^{-})$
are close (we will actually prove they are both close to 0). Since
![]() $I^+ = \lfloor(|x|+2\theta)N\rfloor$
, we have
$I^+ = \lfloor(|x|+2\theta)N\rfloor$
, we have
![]() $u_N^{-}(t)=u_N(t)$
. Moreover,
$u_N^{-}(t)=u_N(t)$
. Moreover,
![]() $\ell^{-}(T_N,\lfloor N(|x|+2\theta) \rfloor)=\ell^{-}(T_N,I^+)=0$
, so
$\ell^{-}(T_N,\lfloor N(|x|+2\theta) \rfloor)=\ell^{-}(T_N,I^+)=0$
, so
![]() $Y_N^{-}(|x|+2\theta)=0$
, and hence
$Y_N^{-}(|x|+2\theta)=0$
, and hence
![]() $r_N^{-}(t)=0$
. Furthermore,
$r_N^{-}(t)=0$
. Furthermore,
![]() $|r_N(t)|\leq |Y_N((|x|+2\theta)^{-})|$
. Therefore we only have to prove that
$|r_N(t)|\leq |Y_N((|x|+2\theta)^{-})|$
. Therefore we only have to prove that
![]() $|Y_N((|x|+2\theta)^{-})| \leq 2N^{-1/12}$
when N is large enough. In addition,
$|Y_N((|x|+2\theta)^{-})| \leq 2N^{-1/12}$
when N is large enough. In addition,
![]() $\mathcal{B}^c$
occurs; thus by Lemma 12 we have
$\mathcal{B}^c$
occurs; thus by Lemma 12 we have
![]() $|Y_N((|x|+2\theta)^{-})-Y_N^{-}((|x|+2\theta)^{-})| \leq N^{-1/12}$
when N is large enough. Moreover, by the definition of
$|Y_N((|x|+2\theta)^{-})-Y_N^{-}((|x|+2\theta)^{-})| \leq N^{-1/12}$
when N is large enough. Moreover, by the definition of
![]() $Y_N^{-}$
and by (1), we have
$Y_N^{-}$
and by (1), we have
and since
![]() $\mathcal{B}$
occurs,
$\mathcal{B}$
occurs,
![]() $(\mathcal{B}_2)^c$
occurs, which means we get
$(\mathcal{B}_2)^c$
occurs, which means we get
Since
![]() $Y_N^{-}(|x|+2\theta)=0$
, this yields
$Y_N^{-}(|x|+2\theta)=0$
, this yields
![]() $\big|Y_N^{-}((|x|+2\theta)^{-})\big|\leq N^{-1/4}$
, which implies
$\big|Y_N^{-}((|x|+2\theta)^{-})\big|\leq N^{-1/4}$
, which implies
![]() $|Y_N((|x|+2\theta)^{-})| \leq N^{-1/12}+N^{-1/4}< 2N^{-1/12}$
. This is enough to complete the proof of Lemma 14.
$|Y_N((|x|+2\theta)^{-})| \leq N^{-1/12}+N^{-1/4}< 2N^{-1/12}$
. This is enough to complete the proof of Lemma 14.
Proof
of Lemma 15. This lemma deals with the ‘right part’ of the parametric representations in the case
![]() $I^+ > \lfloor(|x|+2\theta)N\rfloor$
, and with the ‘left part’ in the case
$I^+ > \lfloor(|x|+2\theta)N\rfloor$
, and with the ‘left part’ in the case
![]() $I^{-} < -\lfloor(|x|+2\theta)N\rfloor$
, corresponding to Panels (b), (c), and (d) of Figure 2. We first give an idea of the argument. The most important part of the proof is to deal with the step corresponding to Figure 2(b). In this step, the function
$I^{-} < -\lfloor(|x|+2\theta)N\rfloor$
, corresponding to Panels (b), (c), and (d) of Figure 2. We first give an idea of the argument. The most important part of the proof is to deal with the step corresponding to Figure 2(b). In this step, the function
![]() $Y_N^{-}(y)=\frac{1}{\sqrt{N}}\ell^{-}\big(T_N,\lfloor Ny\rfloor\big)$
evolves as a sum of
$Y_N^{-}(y)=\frac{1}{\sqrt{N}}\ell^{-}\big(T_N,\lfloor Ny\rfloor\big)$
evolves as a sum of
![]() $\frac{1}{\sqrt{N}}\eta_{j,+}(\ell^{-}(T_N,j))$
by (1), which is close to the sum of
$\frac{1}{\sqrt{N}}\eta_{j,+}(\ell^{-}(T_N,j))$
by (1), which is close to the sum of
![]() $\frac{1}{\sqrt{N}}\big(\zeta_j-\frac{1}{2}\big)$
as
$\frac{1}{\sqrt{N}}\big(\zeta_j-\frac{1}{2}\big)$
as
![]() $\big(\mathcal{B}_4^+\big)^c$
occurs. Since the
$\big(\mathcal{B}_4^+\big)^c$
occurs. Since the
![]() $\zeta_j$
are i.i.d. with mean 0, the sum of
$\zeta_j$
are i.i.d. with mean 0, the sum of
![]() $\frac{1}{\sqrt{N}}\zeta_j$
will be small, and the evolution of
$\frac{1}{\sqrt{N}}\zeta_j$
will be small, and the evolution of
![]() $Y_N^{-}$
will be close to that of a deterministic sum of
$Y_N^{-}$
will be close to that of a deterministic sum of
![]() $-\frac{1}{2\sqrt{N}}$
. Thus it reaches 0 at constant speed, which is also what our parametric representation of
$-\frac{1}{2\sqrt{N}}$
. Thus it reaches 0 at constant speed, which is also what our parametric representation of
![]() $Y_N$
does.
$Y_N$
does.
We now give the proof, beginning with the details of the argument to deal with
![]() $\mathcal{B}^c \cap \{I^{-} < -\lfloor(|x|+2\theta)N\rfloor\}$
. Let us assume
$\mathcal{B}^c \cap \{I^{-} < -\lfloor(|x|+2\theta)N\rfloor\}$
. Let us assume
![]() $\mathcal{B}^c$
occurs and
$\mathcal{B}^c$
occurs and
![]() $I^{-} < -\lfloor(|x|+2\theta)N\rfloor$
. We first see that
$I^{-} < -\lfloor(|x|+2\theta)N\rfloor$
. We first see that
![]() $\frac{I^{-}}{N} \geq -a$
, as since
$\frac{I^{-}}{N} \geq -a$
, as since
![]() $\mathcal{B}^c$
occurs we have
$\mathcal{B}^c$
occurs we have
![]() $|I^{-}+(|x|+2\theta)N| < N^{3/4}$
, which implies
$|I^{-}+(|x|+2\theta)N| < N^{3/4}$
, which implies
![]() $\frac{I^{-}}{N} > -|x|-2\theta - N^{-1/4}$
, and by assumption
$\frac{I^{-}}{N} > -|x|-2\theta - N^{-1/4}$
, and by assumption
![]() $a>|x|+2\theta+N^{-1/8}$
, so
$a>|x|+2\theta+N^{-1/8}$
, so
![]() $-a<-|x|-2\theta-N^{-1/8}<\frac{I^{-}}{N}$
, which implies
$-a<-|x|-2\theta-N^{-1/8}<\frac{I^{-}}{N}$
, which implies
![]() $\frac{I^{-}}{N} \geq -a$
. Moreover, in the part of the parametric representations corresponding to Figure 2(d), we have
$\frac{I^{-}}{N} \geq -a$
. Moreover, in the part of the parametric representations corresponding to Figure 2(d), we have
![]() $\big(u_N^{-}(t),r_N^{-}(t)\big)=(u_N(t),r_N(t))$
. We now consider the equivalent of Figure 2(c). Then
$\big(u_N^{-}(t),r_N^{-}(t)\big)=(u_N(t),r_N(t))$
. We now consider the equivalent of Figure 2(c). Then
![]() $r_N^{-}(t)=r_N(t)=0$
, and
$r_N^{-}(t)=r_N(t)=0$
, and
![]() $\big|u_N^{-}(t)-u_N(t)\big| \leq \big|\frac{I^{-}}{N}+(|x|+2\theta)\big|$
, which is strictly smaller than
$\big|u_N^{-}(t)-u_N(t)\big| \leq \big|\frac{I^{-}}{N}+(|x|+2\theta)\big|$
, which is strictly smaller than
![]() $2N^{-1/12}$
since
$2N^{-1/12}$
since
![]() $|I^{-}+(|x|+2\theta)N| < N^{3/4}$
. It remains to consider the equivalent of Figure 2(b). Then
$|I^{-}+(|x|+2\theta)N| < N^{3/4}$
. It remains to consider the equivalent of Figure 2(b). Then
![]() $\big|u_N^{-}(t)-u_N(t)\big| \leq \big|\frac{I^{-}}{N}+(|x|+2\theta)\big|$
, which is strictly smaller than
$\big|u_N^{-}(t)-u_N(t)\big| \leq \big|\frac{I^{-}}{N}+(|x|+2\theta)\big|$
, which is strictly smaller than
![]() $2N^{-1/12}$
, so we only have to prove
$2N^{-1/12}$
, so we only have to prove
![]() $\big|r_N^{-}(t)-r_N(t)\big| \leq 2N^{-1/12}$
.
$\big|r_N^{-}(t)-r_N(t)\big| \leq 2N^{-1/12}$
.
We are going to study
 \begin{equation*}\sup_{y\in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\bigg|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor (|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2\sqrt{N}}\bigg|.\end{equation*}
\begin{equation*}\sup_{y\in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\bigg|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor (|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2\sqrt{N}}\bigg|.\end{equation*}
Let
![]() $y\in\big[\frac{I^{-}}{N},-|x|-2\theta\big]$
. By the definition of
$y\in\big[\frac{I^{-}}{N},-|x|-2\theta\big]$
. By the definition of
![]() $Y_N^{-}$
we have
$Y_N^{-}$
we have
By (2) and since
![]() $(\mathcal{B}_2)^c$
occurs (remembering that
$(\mathcal{B}_2)^c$
occurs (remembering that
![]() $\lfloor Ny\rfloor \geq I^{-} \geq -(|x|+2\theta)N-N^{3/4} \geq -\lceil2(|x|+2\theta)N\rceil$
), we deduce that
$\lfloor Ny\rfloor \geq I^{-} \geq -(|x|+2\theta)N-N^{3/4} \geq -\lceil2(|x|+2\theta)N\rceil$
), we deduce that
 \begin{equation*} =\left|\frac{\eta_{\lfloor Ny\rfloor,-}\big(\ell^+\big(T_N,\lfloor Ny\rfloor\big)\big)-\eta_{\lfloor -(|x|+2\theta)N\rfloor,-}\big(\ell^+\big(T_N,\lfloor -(|x|+2\theta)N\rfloor\big)\big)}{\sqrt{N}}\right|\leq \frac{2N^{1/16}}{\sqrt{N}}. \end{equation*}
\begin{equation*} =\left|\frac{\eta_{\lfloor Ny\rfloor,-}\big(\ell^+\big(T_N,\lfloor Ny\rfloor\big)\big)-\eta_{\lfloor -(|x|+2\theta)N\rfloor,-}\big(\ell^+\big(T_N,\lfloor -(|x|+2\theta)N\rfloor\big)\big)}{\sqrt{N}}\right|\leq \frac{2N^{1/16}}{\sqrt{N}}. \end{equation*}
In addition, (1) yields the following:
 \begin{equation*} =\sum_{i=\lfloor Ny\rfloor+1}^{\chi(N)-1}(\eta_{i,-}(\ell^+(T_N,i))+\mathbb{1}_{\{i>0\}})-\sum_{i=\lfloor -(|x|+2\theta)N \rfloor+1}^{\chi(N)-1}(\eta_{i,-}(\ell^+(T_N,i))+\mathbb{1}_{\{i>0\}}) \end{equation*}
\begin{equation*} =\sum_{i=\lfloor Ny\rfloor+1}^{\chi(N)-1}(\eta_{i,-}(\ell^+(T_N,i))+\mathbb{1}_{\{i>0\}})-\sum_{i=\lfloor -(|x|+2\theta)N \rfloor+1}^{\chi(N)-1}(\eta_{i,-}(\ell^+(T_N,i))+\mathbb{1}_{\{i>0\}}) \end{equation*}
 \begin{equation*} =\sum_{i=\lfloor Ny\rfloor+1}^{\chi(N)-1}\big(\eta_{i,-}\big(\ell^+\big(T_N,i\big)\big)+1/2\big)\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \end{equation*}
\begin{equation*} =\sum_{i=\lfloor Ny\rfloor+1}^{\chi(N)-1}\big(\eta_{i,-}\big(\ell^+\big(T_N,i\big)\big)+1/2\big)\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \end{equation*}
 \begin{equation*} \qquad\qquad\qquad-\sum_{i=\lfloor -(|x|+2\theta)N \rfloor+1}^{\chi(N)-1}\big(\eta_{i,-}\big(\ell^+\big(T_N,i\big)\big)+1/2\big)-\frac{\lfloor -(|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2}. \end{equation*}
\begin{equation*} \qquad\qquad\qquad-\sum_{i=\lfloor -(|x|+2\theta)N \rfloor+1}^{\chi(N)-1}\big(\eta_{i,-}\big(\ell^+\big(T_N,i\big)\big)+1/2\big)-\frac{\lfloor -(|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2}. \end{equation*}
Since
![]() $\big(\mathcal{B}_4^{-}\big)^c$
occurs, this yields
$\big(\mathcal{B}_4^{-}\big)^c$
occurs, this yields
 \begin{align*}&\left|\ell^+\big(T_N,\lfloor Ny\rfloor\big)-\ell^+\big(T_N,\lfloor -(|x|+2\theta)N \rfloor\big)+\frac{\lfloor-(|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2} \right| \\[4pt]& \qquad \leq \left|\sum_{i=\lfloor Ny\rfloor+1}^{\chi(N)-1}\zeta_i-\sum_{i=\lfloor -(|x|+2\theta)N \rfloor+1}^{\chi(N)-1}\zeta_i \right|+2N^{1/3}\\[4pt]& \qquad = \left|\sum_{i=\lfloor Ny\rfloor+1}^{\lfloor -(|x|+2\theta)N \rfloor}\zeta_i \right|+2N^{1/3}. \end{align*}
\begin{align*}&\left|\ell^+\big(T_N,\lfloor Ny\rfloor\big)-\ell^+\big(T_N,\lfloor -(|x|+2\theta)N \rfloor\big)+\frac{\lfloor-(|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2} \right| \\[4pt]& \qquad \leq \left|\sum_{i=\lfloor Ny\rfloor+1}^{\chi(N)-1}\zeta_i-\sum_{i=\lfloor -(|x|+2\theta)N \rfloor+1}^{\chi(N)-1}\zeta_i \right|+2N^{1/3}\\[4pt]& \qquad = \left|\sum_{i=\lfloor Ny\rfloor+1}^{\lfloor -(|x|+2\theta)N \rfloor}\zeta_i \right|+2N^{1/3}. \end{align*}
As we also have
this implies
 \begin{align*}&\sup_{y\in\big[\frac{I^{-}}{N},-|x|-2\theta\big]} \left|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor (|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2\sqrt{N}} \right|\\& \qquad \leq \max_{I^{-}+1 \leq i \leq \lfloor -(|x|+2\theta)N \rfloor}\frac{1}{\sqrt{N}} \left|\sum_{j=i}^{\lfloor -(|x|+2\theta)N \rfloor} \zeta_j \right| +\frac{2N^{1/16}}{\sqrt{N}}+\frac{2N^{1/3}}{\sqrt{N}}.\end{align*}
\begin{align*}&\sup_{y\in\big[\frac{I^{-}}{N},-|x|-2\theta\big]} \left|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor (|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2\sqrt{N}} \right|\\& \qquad \leq \max_{I^{-}+1 \leq i \leq \lfloor -(|x|+2\theta)N \rfloor}\frac{1}{\sqrt{N}} \left|\sum_{j=i}^{\lfloor -(|x|+2\theta)N \rfloor} \zeta_j \right| +\frac{2N^{1/16}}{\sqrt{N}}+\frac{2N^{1/3}}{\sqrt{N}}.\end{align*}
Moreover,
![]() $\mathcal{B}^c$
occurs, and hence
$\mathcal{B}^c$
occurs, and hence
![]() $|I^{-}+(|x|+2\theta)N| < N^{3/4}$
and
$|I^{-}+(|x|+2\theta)N| < N^{3/4}$
and
![]() $\big(\mathcal{B}_3^{-}\big)^c$
occurs; therefore we obtain that
$\big(\mathcal{B}_3^{-}\big)^c$
occurs; therefore we obtain that
![]() $\sup_{y\in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\Big|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor (|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2\sqrt{N}}\Big|$
is smaller than the quantity
$\sup_{y\in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\Big|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor (|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2\sqrt{N}}\Big|$
is smaller than the quantity
 \begin{align*}&\max_{ -\lfloor(|x|+2\theta)N \rfloor - N^{3/4} \leq i \leq \lfloor -(|x|+2\theta)N\rfloor}\frac{1}{\sqrt{N}} \left|\sum_{j=i}^{\lfloor -(|x|+2\theta)N \rfloor} \zeta_j \right| +\frac{2N^{1/16}}{\sqrt{N}}+\frac{2N^{1/3}}{\sqrt{N}} \\& \qquad \leq \frac{N^{19/48}}{\sqrt{N}}+\frac{2N^{1/16}}{\sqrt{N}}+\frac{2N^{1/3}}{\sqrt{N}} \leq 2 N^{-5/48} \end{align*}
\begin{align*}&\max_{ -\lfloor(|x|+2\theta)N \rfloor - N^{3/4} \leq i \leq \lfloor -(|x|+2\theta)N\rfloor}\frac{1}{\sqrt{N}} \left|\sum_{j=i}^{\lfloor -(|x|+2\theta)N \rfloor} \zeta_j \right| +\frac{2N^{1/16}}{\sqrt{N}}+\frac{2N^{1/3}}{\sqrt{N}} \\& \qquad \leq \frac{N^{19/48}}{\sqrt{N}}+\frac{2N^{1/16}}{\sqrt{N}}+\frac{2N^{1/3}}{\sqrt{N}} \leq 2 N^{-5/48} \end{align*}
when N is large enough. This yields
![]() $\sup_{y\in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\big|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor (|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2\sqrt{N}}\big|\leq 2 N^{-5/48}$
when N is large enough.
$\sup_{y\in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\big|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor (|x|+2\theta)N \rfloor-\lfloor Ny\rfloor}{2\sqrt{N}}\big|\leq 2 N^{-5/48}$
when N is large enough.
We also need an explicit expression for the parametric representations. Assume the part of [0,1] devoted to the equivalent of Figure 2(b) in the parametric representations is
![]() $[a_N,a^{\prime}_N]$
. We set
$[a_N,a^{\prime}_N]$
. We set
![]() $\phi$
equal to the affine function mapping
$\phi$
equal to the affine function mapping
![]() $a_N$
to
$a_N$
to
![]() $-\frac{2I^{-}}{N}$
and
$-\frac{2I^{-}}{N}$
and
![]() $a^{\prime}_N$
to
$a^{\prime}_N$
to
![]() $-(|x|+2\theta)N$
. Then, if
$-(|x|+2\theta)N$
. Then, if
![]() $\phi(t)$
belongs to some
$\phi(t)$
belongs to some
![]() $\big[\frac{2i}{N},\frac{2i+1}{N}\big)$
with
$\big[\frac{2i}{N},\frac{2i+1}{N}\big)$
with
![]() $i\in\{I^{-},\ldots,-\lfloor(|x|+2\theta)N\rfloor-1\}$
, we set
$i\in\{I^{-},\ldots,-\lfloor(|x|+2\theta)N\rfloor-1\}$
, we set
![]() $\big(u_N^{-}(t),r_N^{-}(t)\big)=\big(\phi(t)-\frac{i}{N},Y_N^{-}\big(\phi(t)-\frac{i}{N}\big)\big)$
, while if
$\big(u_N^{-}(t),r_N^{-}(t)\big)=\big(\phi(t)-\frac{i}{N},Y_N^{-}\big(\phi(t)-\frac{i}{N}\big)\big)$
, while if
![]() $\phi(t)$
belongs to some
$\phi(t)$
belongs to some
![]() $\big[\frac{2i+1}{N},\frac{2i+2}{N}\big]$
for
$\big[\frac{2i+1}{N},\frac{2i+2}{N}\big]$
for
![]() $i\in\{I^{-},\ldots,-\lfloor(|x|+2\theta)N\rfloor-1\}$
, we set
$i\in\{I^{-},\ldots,-\lfloor(|x|+2\theta)N\rfloor-1\}$
, we set
 \begin{equation*}\big(u_N^{-}(t),r_N^{-}(t)\big)=\left(\frac{i+1}{N},({-}N\phi(t)+2i+2)Y_N^{-}\left(\left(\frac{i+1}{N}\right)^{-}\right)+(N\phi(t)-2i-1)Y_N^{-}\left(\frac{i+1}{N}\right) \right).\end{equation*}
\begin{equation*}\big(u_N^{-}(t),r_N^{-}(t)\big)=\left(\frac{i+1}{N},({-}N\phi(t)+2i+2)Y_N^{-}\left(\left(\frac{i+1}{N}\right)^{-}\right)+(N\phi(t)-2i-1)Y_N^{-}\left(\frac{i+1}{N}\right) \right).\end{equation*}
In addition, we set
![]() $(u_N(t),r_N(t))=({-}|x|-2\theta,\hat\phi(\phi(t)))$
, where
$(u_N(t),r_N(t))=({-}|x|-2\theta,\hat\phi(\phi(t)))$
, where
![]() $\hat\phi$
is the affine function mapping
$\hat\phi$
is the affine function mapping
![]() $-|x|-2\theta-\frac{\lfloor (|x|+2\theta)N\rfloor+1}{N}$
to
$-|x|-2\theta-\frac{\lfloor (|x|+2\theta)N\rfloor+1}{N}$
to
![]() $Y_N({-}|x|-2\theta)$
and
$Y_N({-}|x|-2\theta)$
and
![]() $\frac{2I^{-}}{N}$
to 0.
$\frac{2I^{-}}{N}$
to 0.
We recall that it is enough to prove
![]() $\big|r_N^{-}(t)-r_N(t)\big| < 2N^{-1/12}$
. We are going to study
$\big|r_N^{-}(t)-r_N(t)\big| < 2N^{-1/12}$
. We are going to study
![]() $\big|r_N^{-}(t)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\big|$
. We first suppose that
$\big|r_N^{-}(t)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\big|$
. We first suppose that
![]() $\phi(t)\in\big[\frac{2i}{N},\frac{2i+1}{N}\big)$
with
$\phi(t)\in\big[\frac{2i}{N},\frac{2i+1}{N}\big)$
with
![]() $i\in\{I^{-},\ldots,-\lfloor (|x|+2\theta)N \rfloor-1\}$
. In this case,
$i\in\{I^{-},\ldots,-\lfloor (|x|+2\theta)N \rfloor-1\}$
. In this case,
![]() $r_N^{-}(t)=Y_N^{-}\big(\phi(t)-\frac{i}{N}\big)$
and
$r_N^{-}(t)=Y_N^{-}\big(\phi(t)-\frac{i}{N}\big)$
and
![]() $\big|\frac{\phi(t)}{2}-\frac{1}{N}\lfloor N\big(\phi(t)-\frac{i}{N}\big)\rfloor\big| = \big|\frac{\phi(t)}{2}-\frac{i}{N}\big| \leq \frac{1}{2N}$
; hence
$\big|\frac{\phi(t)}{2}-\frac{1}{N}\lfloor N\big(\phi(t)-\frac{i}{N}\big)\rfloor\big| = \big|\frac{\phi(t)}{2}-\frac{i}{N}\big| \leq \frac{1}{2N}$
; hence
 \begin{equation*} \left|r_N^{-}(t)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} \left|r_N^{-}(t)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} = \left|Y_N^{-}\left(\phi(t)-\frac{i}{N}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor N\big(\phi(t)-\frac{i}{N}\big)\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right. \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\left.+\frac{\frac{N}{2}\phi(t)-\lfloor N\big(\phi(t)-\frac{i}{N}\big)\rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} = \left|Y_N^{-}\left(\phi(t)-\frac{i}{N}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor N\big(\phi(t)-\frac{i}{N}\big)\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right. \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\left.+\frac{\frac{N}{2}\phi(t)-\lfloor N\big(\phi(t)-\frac{i}{N}\big)\rfloor}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} \leq \left|Y_N^{-}\left(\phi(t)-\frac{i}{N}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor N\big(\phi(t)-\frac{i}{N}\big)\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right|\qquad\qquad \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad+\frac{\sqrt{N}}{2}\left|\frac{\phi(t)}{2}-\frac{1}{N}\left\lfloor N\left(\phi(t)-\frac{i}{N}\right)\right\rfloor\right| \end{equation*}
\begin{equation*} \leq \left|Y_N^{-}\left(\phi(t)-\frac{i}{N}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor N\big(\phi(t)-\frac{i}{N}\big)\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right|\qquad\qquad \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad+\frac{\sqrt{N}}{2}\left|\frac{\phi(t)}{2}-\frac{1}{N}\left\lfloor N\left(\phi(t)-\frac{i}{N}\right)\right\rfloor\right| \end{equation*}
is smaller than
![]() $2N^{-5/48}+\frac{1}{4\sqrt{N}}$
, which implies
$2N^{-5/48}+\frac{1}{4\sqrt{N}}$
, which implies
We now consider the case
![]() $\phi(t)\in\big[\frac{2i+1}{N},\frac{2i+2}{N}\big]$
with
$\phi(t)\in\big[\frac{2i+1}{N},\frac{2i+2}{N}\big]$
with
![]() $i\in\{I^{-},\ldots,-\lfloor (|x|+2\theta)N \rfloor-1\}$
. We temporarily denote
$i\in\{I^{-},\ldots,-\lfloor (|x|+2\theta)N \rfloor-1\}$
. We temporarily denote
![]() $N\phi(t)-2i-1$
by
$N\phi(t)-2i-1$
by
![]() $\varepsilon$
for short, with
$\varepsilon$
for short, with
![]() $\varepsilon \in [0,1]$
. Then we have
$\varepsilon \in [0,1]$
. Then we have
![]() $r_N^{-}(t)=(1-\varepsilon)Y_N^{-}\big(\big(\frac{i+1}{N}\big)^{-}\big)+\varepsilon Y_N^{-}\big(\frac{i+1}{N}\big)$
,
$r_N^{-}(t)=(1-\varepsilon)Y_N^{-}\big(\big(\frac{i+1}{N}\big)^{-}\big)+\varepsilon Y_N^{-}\big(\frac{i+1}{N}\big)$
,
![]() $\big|\frac{\phi(t)}{2}-\frac{i}{N}\big| \leq \frac{1}{N}$
, and
$\big|\frac{\phi(t)}{2}-\frac{i}{N}\big| \leq \frac{1}{N}$
, and
![]() $\big|\frac{\phi(t)}{2}-\frac{i+1}{N}\big| \leq \frac{1}{2N}$
. Therefore,
$\big|\frac{\phi(t)}{2}-\frac{i+1}{N}\big| \leq \frac{1}{2N}$
. Therefore,
 \begin{equation*} \left|r_N^{-}(t)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} \left|r_N^{-}(t)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} =\left|(1-\varepsilon)\left(Y_N^{-}\left(\left(\frac{i+1}{N}\right)^{-}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right)\right. \end{equation*}
\begin{equation*} =\left|(1-\varepsilon)\left(Y_N^{-}\left(\left(\frac{i+1}{N}\right)^{-}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right)\right. \end{equation*}
 \begin{equation*} +\left.\varepsilon \left(Y_N^{-}\left(\frac{i+1}{N}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right)\right| \end{equation*}
\begin{equation*} +\left.\varepsilon \left(Y_N^{-}\left(\frac{i+1}{N}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right)\right| \end{equation*}
 \begin{equation*} \leq (1-\varepsilon)\left|Y_N^{-}\left(\left(\frac{i+1}{N}\right)^{-}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} \leq (1-\varepsilon)\left|Y_N^{-}\left(\left(\frac{i+1}{N}\right)^{-}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} +\,\varepsilon\left|Y_N^{-}\left(\frac{i+1}{N}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} +\,\varepsilon\left|Y_N^{-}\left(\frac{i+1}{N}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} \leq (1-\varepsilon)\left|Y_N^{-}\left(\left(\frac{i+1}{N}\right)^{-}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{i-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} \leq (1-\varepsilon)\left|Y_N^{-}\left(\left(\frac{i+1}{N}\right)^{-}\right)-Y_N^{-}({-}|x|-2\theta)+\frac{i-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} +\,(1-\varepsilon)\left|\frac{\sqrt{N}}{4}\phi(t)-\frac{i}{2\sqrt{N}}\right|+\varepsilon\left|\frac{\sqrt{N}}{4}\phi(t)-\frac{i+1}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} +\,(1-\varepsilon)\left|\frac{\sqrt{N}}{4}\phi(t)-\frac{i}{2\sqrt{N}}\right|+\varepsilon\left|\frac{\sqrt{N}}{4}\phi(t)-\frac{i+1}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} \leq (1-\varepsilon)\sup_{y \in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\left|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor Ny\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} \leq (1-\varepsilon)\sup_{y \in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\left|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor Ny\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} +\,\varepsilon\sup_{y \in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\left|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor Ny\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} +\,\varepsilon\sup_{y \in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\left|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor Ny\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} \leq \sup_{y \in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\left|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor Ny\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right|+\frac{1}{2\sqrt{N}} \end{equation*}
\begin{equation*} \leq \sup_{y \in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\left|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor Ny\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right|+\frac{1}{2\sqrt{N}} \end{equation*}
thanks to our bound on the supremum. Since this was also true for
![]() $\phi(t)\in\big[\frac{2i}{N},\frac{2i+1}{N}\big)$
with
$\phi(t)\in\big[\frac{2i}{N},\frac{2i+1}{N}\big)$
with
![]() $i\in\{I^{-},\ldots,-\lfloor (|x|+2\theta)N \rfloor-1\}$
, we have
$i\in\{I^{-},\ldots,-\lfloor (|x|+2\theta)N \rfloor-1\}$
, we have
The latter expression yields
 \begin{align*} \big|r_N^{-}(t)-r_N(t)\big| &\leq \bigg|r_N(t)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\bigg|+2N^{-5/48}+\frac{1}{2\sqrt{N}} \\[5pt] &=\bigg|\hat\phi(\phi(t))-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\bigg|+2N^{-5/48}+\frac{1}{2\sqrt{N}}, \end{align*}
\begin{align*} \big|r_N^{-}(t)-r_N(t)\big| &\leq \bigg|r_N(t)-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\bigg|+2N^{-5/48}+\frac{1}{2\sqrt{N}} \\[5pt] &=\bigg|\hat\phi(\phi(t))-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\bigg|+2N^{-5/48}+\frac{1}{2\sqrt{N}}, \end{align*}
where
![]() $\hat\phi$
is the affine function mapping
$\hat\phi$
is the affine function mapping
![]() $-|x|-2\theta-\frac{\lfloor(|x|+2\theta)N\rfloor+1}{N}$
to
$-|x|-2\theta-\frac{\lfloor(|x|+2\theta)N\rfloor+1}{N}$
to
![]() $Y_N({-}|x|-2\theta)$
and
$Y_N({-}|x|-2\theta)$
and
![]() $\frac{2I^{-}}{N}$
to 0. Therefore it is enough to prove
$\frac{2I^{-}}{N}$
to 0. Therefore it is enough to prove
 \begin{equation*}\left|\hat\phi(\phi(t))-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}} \right| \leq N^{-1/12}+\frac{1}{2\sqrt{N}}\end{equation*}
\begin{equation*}\left|\hat\phi(\phi(t))-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}} \right| \leq N^{-1/12}+\frac{1}{2\sqrt{N}}\end{equation*}
to complete the proof. Now,
![]() $\hat\phi(\phi(t))-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}$
is an affine function of
$\hat\phi(\phi(t))-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}$
is an affine function of
![]() $\phi(t)$
, so it is enough to prove the bound for
$\phi(t)$
, so it is enough to prove the bound for
![]() $\phi(t)=-|x|-2\theta-\frac{\lfloor(|x|+2\theta)N\rfloor+1}{N}$
and for
$\phi(t)=-|x|-2\theta-\frac{\lfloor(|x|+2\theta)N\rfloor+1}{N}$
and for
![]() $\phi(t)=\frac{2I^{-}}{N}$
. We first consider
$\phi(t)=\frac{2I^{-}}{N}$
. We first consider
![]() $\phi(t)=\frac{2I^{-}}{N}$
. By Lemma 6,
$\phi(t)=\frac{2I^{-}}{N}$
. By Lemma 6,
![]() $\ell^{-}(T_N,I^{-}) = 0$
. Moreover,
$\ell^{-}(T_N,I^{-}) = 0$
. Moreover,
![]() $I^{-} < -\lfloor(|x|+2\theta)N\rfloor$
, and hence
$I^{-} < -\lfloor(|x|+2\theta)N\rfloor$
, and hence
![]() $Y_N^{-}\big(\frac{I^{-}}{N}\big)=0$
. We deduce that
$Y_N^{-}\big(\frac{I^{-}}{N}\big)=0$
. We deduce that
 \begin{equation*} \left|\hat\phi(\phi(t))-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} \left|\hat\phi(\phi(t))-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} =\left|-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\frac{2I^{-}}{N}-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} =\left|-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\frac{2I^{-}}{N}-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
 \begin{equation*} \leq \sup_{y \in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\left|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor Ny\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right|\leq 2 N^{-5/48}, \end{equation*}
\begin{equation*} \leq \sup_{y \in\big[\frac{I^{-}}{N},-|x|-2\theta\big]}\left|Y_N^{-}(y)-Y_N^{-}({-}|x|-2\theta)+\frac{\lfloor Ny\rfloor-\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right|\leq 2 N^{-5/48}, \end{equation*}
which is enough. We now consider
![]() $\phi(t)=-|x|-2\theta-\frac{\lfloor(|x|+2\theta)N\rfloor+1}{N}$
. Then
$\phi(t)=-|x|-2\theta-\frac{\lfloor(|x|+2\theta)N\rfloor+1}{N}$
. Then
![]() $\Big|\hat\phi(\phi(t))-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\Big|$
is equal to
$\Big|\hat\phi(\phi(t))-Y_N^{-}({-}|x|-2\theta)+\frac{\sqrt{N}}{4}\phi(t)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\Big|$
is equal to
 \begin{equation*} \qquad\qquad\qquad\qquad\qquad\left.+\,\frac{\sqrt{N}}{4}\left({-}|x|-2\theta-\frac{\lfloor(|x|+2\theta)N\rfloor+1}{N}\right)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
\begin{equation*} \qquad\qquad\qquad\qquad\qquad\left.+\,\frac{\sqrt{N}}{4}\left({-}|x|-2\theta-\frac{\lfloor(|x|+2\theta)N\rfloor+1}{N}\right)-\frac{\lfloor -(|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \end{equation*}
by Lemma 12, which completes the proof for
![]() $\mathcal{B}^c \cap \{I^{-} < -\lfloor(|x|+2\theta)N\rfloor\}$
.
$\mathcal{B}^c \cap \{I^{-} < -\lfloor(|x|+2\theta)N\rfloor\}$
.
The argument to show that
![]() $\mathcal{B}^c \cap \{I^+ > \lfloor(|x|+2\theta)N\rfloor\} \subset \big\{$
between
$\mathcal{B}^c \cap \{I^+ > \lfloor(|x|+2\theta)N\rfloor\} \subset \big\{$
between
![]() $\frac{((|x|+2\theta)N) \wedge I^+}{N}$
and a,
$\frac{((|x|+2\theta)N) \wedge I^+}{N}$
and a,
![]() $\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\big\}$
is similar and simpler, except for the end of the argument, which we give here. In a similar way as in the previous case, we must bound
$\|u_N^{-}-u_N\|_\infty,\|r_N^{-}-r_N\|_\infty \leq 2N^{-1/12}\big\}$
is similar and simpler, except for the end of the argument, which we give here. In a similar way as in the previous case, we must bound
 \begin{align*} &\left|Y_N((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)+\frac{\sqrt{N}}{4}\Big(|x|+2\theta+\frac{\lfloor(|x|+2\theta)N\rfloor}{N}\Big)-\frac{\lfloor (|x|+2\theta)N \rfloor}{2\sqrt{N}} \right| \\ & \qquad \leq \left|Y_N((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta) \right|+ \left|\frac{(|x|+2\theta)N-\lfloor (|x|+2\theta)N \rfloor}{4\sqrt{N}} \right| \\ & \qquad \leq \left|Y_N((|x|+2\theta)^{-})-Y_N^{-}((|x|+2\theta)^{-}) \right|+\left|Y_N^{-}((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta) \right|+\frac{1}{4\sqrt{N}}; \end{align*}
\begin{align*} &\left|Y_N((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)+\frac{\sqrt{N}}{4}\Big(|x|+2\theta+\frac{\lfloor(|x|+2\theta)N\rfloor}{N}\Big)-\frac{\lfloor (|x|+2\theta)N \rfloor}{2\sqrt{N}} \right| \\ & \qquad \leq \left|Y_N((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta) \right|+ \left|\frac{(|x|+2\theta)N-\lfloor (|x|+2\theta)N \rfloor}{4\sqrt{N}} \right| \\ & \qquad \leq \left|Y_N((|x|+2\theta)^{-})-Y_N^{-}((|x|+2\theta)^{-}) \right|+\left|Y_N^{-}((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta) \right|+\frac{1}{4\sqrt{N}}; \end{align*}
hence Lemma 12 yields
 \begin{align*}& \left|Y_N((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)+\frac{\sqrt{N}}{4}\left(|x|+2\theta+\frac{\lfloor(|x|+2\theta)N\rfloor}{N}\right)-\frac{\lfloor (|x|+2\theta)N \rfloor}{2\sqrt{N}} \right| \\& \qquad \leq N^{-1/12}+\big|Y_N^{-}((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)\big|+\frac{1}{4\sqrt{N}}. \end{align*}
\begin{align*}& \left|Y_N((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)+\frac{\sqrt{N}}{4}\left(|x|+2\theta+\frac{\lfloor(|x|+2\theta)N\rfloor}{N}\right)-\frac{\lfloor (|x|+2\theta)N \rfloor}{2\sqrt{N}} \right| \\& \qquad \leq N^{-1/12}+\big|Y_N^{-}((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)\big|+\frac{1}{4\sqrt{N}}. \end{align*}
In addition, the definition of
![]() $Y_N^{-}$
and (1) yield that if
$Y_N^{-}$
and (1) yield that if
![]() $(|x|+2\theta)N$
is not an integer, then
$(|x|+2\theta)N$
is not an integer, then
![]() $Y_N^{-}((|x|+2\theta)^{-})=Y_N^{-}(|x|+2\theta)$
, while if
$Y_N^{-}((|x|+2\theta)^{-})=Y_N^{-}(|x|+2\theta)$
, while if
![]() $(|x|+2\theta)N$
is an integer, then
$(|x|+2\theta)N$
is an integer, then
 \begin{align*}\big|Y_N^{-}((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)\big| &=\frac{1}{\sqrt{N}}\big|\ell^{-}\big(T_N,(|x|+2\theta)N-1\big)-\ell^{-}\big(T_N,(|x|+2\theta)N\big)\big|\\&=\frac{1}{\sqrt{N}}\big|\eta_{(|x|+2\theta)N-1,+}\big(\ell^{-}\big(T_N,(|x|+2\theta)N-1\big)\big)\big| \\&\leq \frac{N^{1/16}+1/2}{\sqrt{N}},\end{align*}
\begin{align*}\big|Y_N^{-}((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)\big| &=\frac{1}{\sqrt{N}}\big|\ell^{-}\big(T_N,(|x|+2\theta)N-1\big)-\ell^{-}\big(T_N,(|x|+2\theta)N\big)\big|\\&=\frac{1}{\sqrt{N}}\big|\eta_{(|x|+2\theta)N-1,+}\big(\ell^{-}\big(T_N,(|x|+2\theta)N-1\big)\big)\big| \\&\leq \frac{N^{1/16}+1/2}{\sqrt{N}},\end{align*}
since
![]() $(\mathcal{B}_2)^c$
occurs. In all cases we obtain
$(\mathcal{B}_2)^c$
occurs. In all cases we obtain
![]() $\big|Y_N^{-}((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)\big|\leq \frac{N^{1/16}+1/2}{\sqrt{N}}$
; therefore,
$\big|Y_N^{-}((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)\big|\leq \frac{N^{1/16}+1/2}{\sqrt{N}}$
; therefore,
 \begin{align*}&\left|Y_N((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)+\frac{\sqrt{N}}{4}\left(|x|+2\theta+\frac{\lfloor(|x|+2\theta)N\rfloor}{N}\right)-\frac{\lfloor (|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \\& \qquad \leq N^{-1/12}+\frac{N^{1/16}+1/2}{\sqrt{N}}+\frac{1}{4\sqrt{N}},\end{align*}
\begin{align*}&\left|Y_N((|x|+2\theta)^{-})-Y_N^{-}(|x|+2\theta)+\frac{\sqrt{N}}{4}\left(|x|+2\theta+\frac{\lfloor(|x|+2\theta)N\rfloor}{N}\right)-\frac{\lfloor (|x|+2\theta)N \rfloor}{2\sqrt{N}}\right| \\& \qquad \leq N^{-1/12}+\frac{N^{1/16}+1/2}{\sqrt{N}}+\frac{1}{4\sqrt{N}},\end{align*}
which is a bound small enough to complete the proof of the lemma.
5. Convergence of the local times process: proof of Theorem 2 and Proposition 3
5.1. Proof of Theorem 2
Our aim is to prove that
![]() $Y_N^\pm$
converges in distribution to
$Y_N^\pm$
converges in distribution to
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
in the Skorokhod
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
in the Skorokhod
![]() $M_1$
topology on
$M_1$
topology on
![]() $D({-}\infty,+\infty)$
when N tends to
$D({-}\infty,+\infty)$
when N tends to
![]() $+\infty$
. Proposition 5 yields that
$+\infty$
. Proposition 5 yields that
![]() $Y_N^\pm$
is close to the function
$Y_N^\pm$
is close to the function
![]() $Y_N$
defined by
$Y_N$
defined by
![]() $Y_N(y)=\frac{1}{\sqrt{N}}\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i$
if
$Y_N(y)=\frac{1}{\sqrt{N}}\sum_{i=\lfloor N y\rfloor+1}^{\chi(N)-1}\zeta_i$
if
![]() $y \in \big[{-}|x|-2\theta,\frac{\chi(N)}{N}\big)$
,
$y \in \big[{-}|x|-2\theta,\frac{\chi(N)}{N}\big)$
,
![]() $Y_N(y)=\frac{1}{\sqrt{N}}\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i$
if
$Y_N(y)=\frac{1}{\sqrt{N}}\sum_{i=\chi(N)}^{\lfloor N y\rfloor-1}\zeta_i$
if
![]() $y \in \big[\frac{\chi(N)}{N},|x|+2\theta\big)$
, and
$y \in \big[\frac{\chi(N)}{N},|x|+2\theta\big)$
, and
![]() $Y_N(y)=0$
otherwise. One has the feeling that by Donsker’s invariance principle,
$Y_N(y)=0$
otherwise. One has the feeling that by Donsker’s invariance principle,
![]() $Y_N$
should converge to
$Y_N$
should converge to
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
, and so we should be able to conclude quickly, but rigorously proving the convergence in the Skorokhod
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
, and so we should be able to conclude quickly, but rigorously proving the convergence in the Skorokhod
![]() $M_1$
topology on
$M_1$
topology on
![]() $D({-}\infty,+\infty)$
is harder than it looks. We are instead going to use a similar argument with a new process
$D({-}\infty,+\infty)$
is harder than it looks. We are instead going to use a similar argument with a new process
![]() $Y^{\prime\prime}_N$
which will be ‘like
$Y^{\prime\prime}_N$
which will be ‘like
![]() $Y_N$
, but continuous in
$Y_N$
, but continuous in
![]() $[{-}|x|-2\theta,|x|+2\theta)$
’. We define it as follows. We first set a process
$[{-}|x|-2\theta,|x|+2\theta)$
’. We define it as follows. We first set a process
![]() $Y^{\prime}_N$
thus: if
$Y^{\prime}_N$
thus: if
![]() $Ny\in\mathbb{Z}$
, then
$Ny\in\mathbb{Z}$
, then
![]() $Y^{\prime}_N(y)=\frac{1}{\sqrt{N}}\sum_{i= N y+1}^{\chi(N)-1}\zeta_i$
if
$Y^{\prime}_N(y)=\frac{1}{\sqrt{N}}\sum_{i= N y+1}^{\chi(N)-1}\zeta_i$
if
![]() $y \in \big({-}\infty,\frac{\chi(N)}{N}\big)$
and
$y \in \big({-}\infty,\frac{\chi(N)}{N}\big)$
and
![]() $Y^{\prime}_N(y)=\frac{1}{\sqrt{N}}\sum_{i=\chi(N)}^{N y-1}\zeta_i$
if
$Y^{\prime}_N(y)=\frac{1}{\sqrt{N}}\sum_{i=\chi(N)}^{N y-1}\zeta_i$
if
![]() $y \in \big[\frac{\chi(N)}{N},+\infty\big)$
; in between,
$y \in \big[\frac{\chi(N)}{N},+\infty\big)$
; in between,
![]() $Y^{\prime}_N$
is linearly interpolated. We then define
$Y^{\prime}_N$
is linearly interpolated. We then define
![]() $Y^{\prime\prime}_N$
by
$Y^{\prime\prime}_N$
by
![]() $Y^{\prime\prime}_N(y)=Y^{\prime}_N(y)\mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}$
for any
$Y^{\prime\prime}_N(y)=Y^{\prime}_N(y)\mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}$
for any
![]() $y\in\mathbb{R}$
. Then
$y\in\mathbb{R}$
. Then
![]() $Y^{\prime\prime}_N$
will converge to
$Y^{\prime\prime}_N$
will converge to
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
and be close to
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
and be close to
![]() $Y_N$
, as stated in the following two lemmas.
$Y_N$
, as stated in the following two lemmas.
Lemma 16.
![]() $Y^{\prime\prime}_N$
converges to
$Y^{\prime\prime}_N$
converges to
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
in distribution when N tends to
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
in distribution when N tends to
![]() $+\infty$
for the Skorokhod
$+\infty$
for the Skorokhod
![]() $M_1$
topology in
$M_1$
topology in
![]() $D({-}\infty,\infty)$
.
$D({-}\infty,\infty)$
.
Lemma 17.
![]() $\mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y^{\prime\prime}_N\big)>N^{-7/16}\big)$
tends to 0 when N tends to
$\mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y^{\prime\prime}_N\big)>N^{-7/16}\big)$
tends to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
Given these two lemmas, the proof of Theorem 2 is fairly standard. One may for example look at the end of the proof of the Donsker invariance principle in [Reference Mörters and Peres8] (here
![]() $Y^{\prime\prime}_N$
converges to the desired distribution instead of having it outright, but this convergence yields that the probability that
$Y^{\prime\prime}_N$
converges to the desired distribution instead of having it outright, but this convergence yields that the probability that
![]() $Y^{\prime\prime}_N$
is in a closed set has the right limit). Thus we only have to prove Lemmas 16 and 17. In order to do this, we first need two easy lemmas which will also be used later in this work. If we denote by
$Y^{\prime\prime}_N$
is in a closed set has the right limit). Thus we only have to prove Lemmas 16 and 17. In order to do this, we first need two easy lemmas which will also be used later in this work. If we denote by
![]() $C[{-}|x|-2\theta,|x|+2\theta]$
the space of continuous functions
$C[{-}|x|-2\theta,|x|+2\theta]$
the space of continuous functions
![]() $[{-}|x|-2\theta,|x|+2\theta] \mapsto \mathbb{R}$
, then since the
$[{-}|x|-2\theta,|x|+2\theta] \mapsto \mathbb{R}$
, then since the
![]() $(\zeta_i)_{i\in\mathbb{Z}}$
are i.i.d. with law
$(\zeta_i)_{i\in\mathbb{Z}}$
are i.i.d. with law
![]() $\rho_0$
, which is symmetric and so has zero mean, Donsker’s invariance principle yields the following.
$\rho_0$
, which is symmetric and so has zero mean, Donsker’s invariance principle yields the following.
Lemma 18.
![]() $Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}$
converges in distribution to
$Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}$
converges in distribution to
![]() $B^x|_{[{-}|x|-2\theta,|x|+2\theta]}$
when N tends to
$B^x|_{[{-}|x|-2\theta,|x|+2\theta]}$
when N tends to
![]() $+\infty$
for the topology defined on
$+\infty$
for the topology defined on
![]() $C[{-}|x|-2\theta,|x|+2\theta]$
by the uniform norm.
$C[{-}|x|-2\theta,|x|+2\theta]$
by the uniform norm.
The following lemma is also easy to prove.
Lemma 19.
If
![]() $(\mathcal{B}_2)^c$
occurs, then
$(\mathcal{B}_2)^c$
occurs, then
![]() $\sup\{|Y_N(y)-Y^{\prime\prime}_N(y)|\,:\,y\in[{-}|x|-2\theta,|x|+2\theta)\} \leq N^{-7/16}$
.
$\sup\{|Y_N(y)-Y^{\prime\prime}_N(y)|\,:\,y\in[{-}|x|-2\theta,|x|+2\theta)\} \leq N^{-7/16}$
.
Proof. By the definition of
![]() $Y_N$
and
$Y_N$
and
![]() $Y^{\prime\prime}_N$
, we have
$Y^{\prime\prime}_N$
, we have
 \begin{align*} & \sup\big\{\big|Y_N(y)-Y^{\prime\prime}_N(y)\big|\,:\,y\in[{-}|x|-2\theta,|x|+2\theta)\big\}\\& \quad \leq \frac{1}{\sqrt{N}}\sup\{|\zeta_i|\,:\,-(|x|+2\theta)N \leq i \leq (|x|+2\theta)N\},\end{align*}
\begin{align*} & \sup\big\{\big|Y_N(y)-Y^{\prime\prime}_N(y)\big|\,:\,y\in[{-}|x|-2\theta,|x|+2\theta)\big\}\\& \quad \leq \frac{1}{\sqrt{N}}\sup\{|\zeta_i|\,:\,-(|x|+2\theta)N \leq i \leq (|x|+2\theta)N\},\end{align*}
which is smaller than
![]() $\frac{N^{1/16}}{\sqrt{N}}=N^{-7/16}$
if
$\frac{N^{1/16}}{\sqrt{N}}=N^{-7/16}$
if
![]() $(\mathcal{B}_2)^c$
occurs.
$(\mathcal{B}_2)^c$
occurs.
We also need the following technical lemma in order to deduce results on the Skorokhod
![]() $M_1$
topology from Lemmas 18 and 19.
$M_1$
topology from Lemmas 18 and 19.
Lemma 20.
Let
![]() $N>0$
, and let
$N>0$
, and let
![]() $Z_1,Z_2 \in D({-}\infty,+\infty)$
be functions whose possible discontinuities belong to
$Z_1,Z_2 \in D({-}\infty,+\infty)$
be functions whose possible discontinuities belong to
![]() $\frac{1}{N}\mathbb{Z}$
. Then
$\frac{1}{N}\mathbb{Z}$
. Then
Proof. Lemma 20 can be proved by writing, for each
![]() $a \neq |x|+2\theta$
, parametric representations of the two processes on
$a \neq |x|+2\theta$
, parametric representations of the two processes on
![]() $[{-}a,a]$
‘following their completed graphs together’ (one can find an explicit construction of such representations in the first arXiv version of this paper [Reference Marêché5]).
$[{-}a,a]$
‘following their completed graphs together’ (one can find an explicit construction of such representations in the first arXiv version of this paper [Reference Marêché5]).
Lemma 20 will allow us to deduce Lemma 16 from Lemma 18, and Lemma 17 from Lemma 19 and Proposition 5, which will complete the proof of Theorem 2.
Proof
of Lemma 16. Let
![]() $f\,:\,D({-}\infty,+\infty) \mapsto \mathbb{R}$
be bounded and continuous with respect to the Skorokhod
$f\,:\,D({-}\infty,+\infty) \mapsto \mathbb{R}$
be bounded and continuous with respect to the Skorokhod
![]() $M_1$
topology on
$M_1$
topology on
![]() $D({-}\infty,+\infty)$
. We need to prove that
$D({-}\infty,+\infty)$
. We need to prove that
![]() $\mathbb{E}\big(f\big(Y^{\prime\prime}_N\big)\big)$
converges to
$\mathbb{E}\big(f\big(Y^{\prime\prime}_N\big)\big)$
converges to
![]() $\mathbb{E}\big(f\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}\big)\big)$
when N tends to
$\mathbb{E}\big(f\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}\big)\big)$
when N tends to
![]() $+\infty$
. We define
$+\infty$
. We define
![]() $g \,:\, C[{-}|x|-2\theta,|x|+2\theta] \mapsto \mathbb{R}$
by
$g \,:\, C[{-}|x|-2\theta,|x|+2\theta] \mapsto \mathbb{R}$
by
![]() $g(Z)=f\big(\big(Z(y)\mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}\big)$
for any
$g(Z)=f\big(\big(Z(y)\mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}\big)$
for any
![]() $Z \in C[{-}|x|-2\theta,|x|+2\theta]$
. We then have
$Z \in C[{-}|x|-2\theta,|x|+2\theta]$
. We then have
![]() $\mathbb{E}\big(f\big(Y^{\prime\prime}_N\big)\big)=\mathbb{E}\big(g\big(Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}\big)\big)$
and
$\mathbb{E}\big(f\big(Y^{\prime\prime}_N\big)\big)=\mathbb{E}\big(g\big(Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}\big)\big)$
and
![]() $\mathbb{E}\big(f\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}\big)\big)=\mathbb{E}\big(g\big(B^x |_{[{-}|x|-2\theta,|x|+2\theta]}\big)\big)$
; hence it is enough to prove that
$\mathbb{E}\big(f\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}\big)\big)=\mathbb{E}\big(g\big(B^x |_{[{-}|x|-2\theta,|x|+2\theta]}\big)\big)$
; hence it is enough to prove that
![]() $\mathbb{E}\big(g\big(Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}\big)\big)$
converges to
$\mathbb{E}\big(g\big(Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}\big)\big)$
converges to
![]() $\mathbb{E}\big(g\big(B^x |_{[{-}|x|-2\theta,|x|+2\theta]}\big)\big)$
when N tends to
$\mathbb{E}\big(g\big(B^x |_{[{-}|x|-2\theta,|x|+2\theta]}\big)\big)$
when N tends to
![]() $+\infty$
. Furthermore, Lemma 18 yields that
$+\infty$
. Furthermore, Lemma 18 yields that
![]() $Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}$
converges in distribution to
$Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}$
converges in distribution to
![]() $B^x|_{[{-}|x|-2\theta,|x|+2\theta]}$
when N tends to
$B^x|_{[{-}|x|-2\theta,|x|+2\theta]}$
when N tends to
![]() $+\infty$
for the topology defined on
$+\infty$
for the topology defined on
![]() $C[{-}|x|-2\theta,|x|+2\theta]$
by the uniform norm. Consequently, we only have to prove that g is continuous for this topology.
$C[{-}|x|-2\theta,|x|+2\theta]$
by the uniform norm. Consequently, we only have to prove that g is continuous for this topology.
Let
![]() $(Z_k)_{k\in\mathbb{N}}$
be a sequence in
$(Z_k)_{k\in\mathbb{N}}$
be a sequence in
![]() $C[{-}|x|-2\theta,|x|+2\theta]$
converging uniformly to
$C[{-}|x|-2\theta,|x|+2\theta]$
converging uniformly to
![]() $Z \in C[{-}|x|-2\theta,|x|+2\theta]$
when k tends to
$Z \in C[{-}|x|-2\theta,|x|+2\theta]$
when k tends to
![]() $+\infty$
. Then Lemma 20 states that for all
$+\infty$
. Then Lemma 20 states that for all
![]() $k\in\mathbb{N}$
,
$k\in\mathbb{N}$
,
Since the latter tends to 0 when k tends to
![]() $+\infty$
,
$+\infty$
,
![]() $(Z_k(y)\mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}})_{y\in\mathbb{R}}$
converges to
$(Z_k(y)\mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}})_{y\in\mathbb{R}}$
converges to
![]() $\big(Z(y)\mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
when k tends to
$\big(Z(y)\mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
when k tends to
![]() $+\infty$
with respect to the Skorokhod
$+\infty$
with respect to the Skorokhod
![]() $M_1$
topology on
$M_1$
topology on
![]() $D({-}\infty,+\infty)$
. Since f is continuous with respect to this topology,
$D({-}\infty,+\infty)$
. Since f is continuous with respect to this topology,
![]() $(g(Z_k))_{k\in\mathbb{N}}$
converges to g(Z) when k tends to
$(g(Z_k))_{k\in\mathbb{N}}$
converges to g(Z) when k tends to
![]() $+\infty$
. Consequently g is continuous for the topology defined on
$+\infty$
. Consequently g is continuous for the topology defined on
![]() $C[{-}|x|-2\theta,|x|+2\theta]$
by the uniform norm, which completes the proof.
$C[{-}|x|-2\theta,|x|+2\theta]$
by the uniform norm, which completes the proof.
Proof of Lemma 17. We have
when N is large enough. By Lemmas 19 and 20 we have
![]() $\mathbb{P}\big(d_{M_1}\big(Y_N,Y^{\prime\prime}_N\big)>N^{-7/16}\big) \leq \mathbb{P}(\mathcal{B}_2)$
. Therefore
$\mathbb{P}\big(d_{M_1}\big(Y_N,Y^{\prime\prime}_N\big)>N^{-7/16}\big) \leq \mathbb{P}(\mathcal{B}_2)$
. Therefore
![]() $\mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y^{\prime\prime}_N\big)>4N^{-1/12}\big) \leq \mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y_N\big)>3N^{-1/12}\big)+\mathbb{P}(\mathcal{B}_2)$
, which tends to 0 when N tends to
$\mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y^{\prime\prime}_N\big)>4N^{-1/12}\big) \leq \mathbb{P}\big(d_{M_1}\big(Y_N^\pm,Y_N\big)>3N^{-1/12}\big)+\mathbb{P}(\mathcal{B}_2)$
, which tends to 0 when N tends to
![]() $+\infty$
by Proposition 5 and Lemma 3.
$+\infty$
by Proposition 5 and Lemma 3.
5.2. Proof of Proposition 3
Our goal is to prove that for any closed interval
![]() $I\in\mathbb{R}$
that does not contain
$I\in\mathbb{R}$
that does not contain
![]() $-|x|-2\theta$
or
$-|x|-2\theta$
or
![]() $|x|+2\theta$
, the process
$|x|+2\theta$
, the process
![]() $\big(Y_N^\pm(y)\big)_{y\in I}$
converges in distribution to
$\big(Y_N^\pm(y)\big)_{y\in I}$
converges in distribution to
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in I}$
in the topology on D I given by the uniform norm when N tends to
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in I}$
in the topology on D I given by the uniform norm when N tends to
![]() $+\infty$
. We first assume
$+\infty$
. We first assume
![]() $I=[a,b]$
or
$I=[a,b]$
or
![]() $I=[a,+\infty)$
with
$I=[a,+\infty)$
with
![]() $a>|x|+2\theta$
(the case
$a>|x|+2\theta$
(the case
![]() $I=[a,b]$
or
$I=[a,b]$
or
![]() $I=({-}\infty,b]$
with
$I=({-}\infty,b]$
with
![]() $b<-|x|-2\theta$
can be dealt with in the same way). We are going to prove that outside an event of small probability,
$b<-|x|-2\theta$
can be dealt with in the same way). We are going to prove that outside an event of small probability,
![]() $\big(Y_N^\pm(y)\big)_{y\in I}=0=\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in I}$
. For any
$\big(Y_N^\pm(y)\big)_{y\in I}=0=\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in I}$
. For any
![]() $y \geq (|x|+2\theta)\vee\frac{I^+}{N}$
, by Lemma 6 we have
$y \geq (|x|+2\theta)\vee\frac{I^+}{N}$
, by Lemma 6 we have
![]() $\ell^\pm\big(T_N,\lfloor Ny \rfloor\big)=0$
, and thus
$\ell^\pm\big(T_N,\lfloor Ny \rfloor\big)=0$
, and thus
![]() $Y_N^\pm(y)=0$
. We deduce that as soon as
$Y_N^\pm(y)=0$
. We deduce that as soon as
![]() $\frac{I^+}{N} \leq a$
, we have
$\frac{I^+}{N} \leq a$
, we have
![]() $\big(Y_N^\pm(y)\big)_{y\in I}=0=\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in I}$
. In addition, when N is large enough we have
$\big(Y_N^\pm(y)\big)_{y\in I}=0=\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in I}$
. In addition, when N is large enough we have
![]() $a \geq |x|+2\theta+N^{-1/4}$
. Therefore, when N is large enough,
$a \geq |x|+2\theta+N^{-1/4}$
. Therefore, when N is large enough,
which tends to 0 when N tends to
![]() $+\infty$
by Lemma 7. This yields that
$+\infty$
by Lemma 7. This yields that
![]() $\big(Y_N^\pm(y)\big)_{y\in I}$
converges in distribution to
$\big(Y_N^\pm(y)\big)_{y\in I}$
converges in distribution to
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in I}\big)$
in the topology on D I given by the uniform norm.
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in I}\big)$
in the topology on D I given by the uniform norm.
We now deal with the case
![]() $I=[a,b]$
with
$I=[a,b]$
with
![]() $-|x|-2\theta < a < b < |x|+2\theta$
. The idea is that we will be far from the problems at
$-|x|-2\theta < a < b < |x|+2\theta$
. The idea is that we will be far from the problems at
![]() $-|x|-2\theta$
and
$-|x|-2\theta$
and
![]() $|x|+2\theta$
, so that
$|x|+2\theta$
, so that
![]() $Y_N^\pm$
will be close to
$Y_N^\pm$
will be close to
![]() $Y^{\prime}_N$
in all I, and
$Y^{\prime}_N$
in all I, and
![]() $Y^{\prime}_N$
converges to the right limit, which means
$Y^{\prime}_N$
converges to the right limit, which means
![]() $Y_N^\pm$
does as well. We first prove the following lemma.
$Y_N^\pm$
does as well. We first prove the following lemma.
Lemma 21.
For any
![]() $-|x|-2\theta < a < b < |x|+2\theta$
, we have that
$-|x|-2\theta < a < b < |x|+2\theta$
, we have that
![]() $\mathbb{P}\big(\|Y_N^\pm|_{[a,b]}-Y^{\prime}_N|_{[a,b]}\|_\infty > 2N^{-1/12}\big)$
tends to 0 when N tends to
$\mathbb{P}\big(\|Y_N^\pm|_{[a,b]}-Y^{\prime}_N|_{[a,b]}\|_\infty > 2N^{-1/12}\big)$
tends to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
Proof. We assume
![]() $(\mathcal{B}_2)^c$
,
$(\mathcal{B}_2)^c$
,
![]() $\big(\mathcal{B}_4^{-}\big)^c$
, and
$\big(\mathcal{B}_4^{-}\big)^c$
, and
![]() $\big(\mathcal{B}_4^+\big)^c$
occur, as well as
$\big(\mathcal{B}_4^+\big)^c$
occur, as well as
![]() $|I^{-}+(|x|+2\theta)N|< N^{3/4}$
,
$|I^{-}+(|x|+2\theta)N|< N^{3/4}$
,
![]() $|I^+-(|x|+2\theta)N|< N^{3/4}$
. When N is large enough, we have
$|I^+-(|x|+2\theta)N|< N^{3/4}$
. When N is large enough, we have
![]() $a \geq -|x|-2\theta+N^{-1/4} > \frac{I^{-}}{N}$
and
$a \geq -|x|-2\theta+N^{-1/4} > \frac{I^{-}}{N}$
and
![]() $b \leq |x|+2\theta-N^{-1/4} < \frac{I^+}{N}$
, so
$b \leq |x|+2\theta-N^{-1/4} < \frac{I^+}{N}$
, so
![]() $[a,b] \subset \big(\frac{I^{-}}{N},\frac{I^+}{N}\big)$
. Therefore, for any
$[a,b] \subset \big(\frac{I^{-}}{N},\frac{I^+}{N}\big)$
. Therefore, for any
![]() $y\in[a,b]$
, Lemma 12 yields
$y\in[a,b]$
, Lemma 12 yields
![]() $\big|Y_N^\pm(y)-Y_N(y)\big| \leq N^{-1/12}$
, and Lemma 19 gives
$\big|Y_N^\pm(y)-Y_N(y)\big| \leq N^{-1/12}$
, and Lemma 19 gives
![]() $\big|Y_N(y)-Y^{\prime}_N(y)\big| \leq N^{-7/16}$
. Hence we get
$\big|Y_N(y)-Y^{\prime}_N(y)\big| \leq N^{-7/16}$
. Hence we get
![]() $\big|Y_N^\pm(y)-Y^{\prime}_N(y)\big| \leq 2N^{-1/12}$
, and we deduce
$\big|Y_N^\pm(y)-Y^{\prime}_N(y)\big| \leq 2N^{-1/12}$
, and we deduce
![]() $\big\|Y_N^\pm|_{[a,b]}-Y^{\prime}_N|_{[a,b]}\big\|_\infty \leq 2N^{-1/12}$
. This implies
$\big\|Y_N^\pm|_{[a,b]}-Y^{\prime}_N|_{[a,b]}\big\|_\infty \leq 2N^{-1/12}$
. This implies
 \begin{align*}&\mathbb{P}\big(\big\|Y_N^\pm|_{[a,b]}-Y^{\prime}_N|_{[a,b]}\big\|_\infty > 2N^{-1/12}\big) \\&\qquad \leq \mathbb{P}\big(\mathcal{B}_2\cup\mathcal{B}_4^{-}\cup\mathcal{B}_4^+ \cup \big\{|I^{-}+(|x|+2\theta)N| \geq N^{3/4}\big\} \cup \big\{|I^+-(|x|+2\theta)N| \geq N^{3/4}\big\}\big), \end{align*}
\begin{align*}&\mathbb{P}\big(\big\|Y_N^\pm|_{[a,b]}-Y^{\prime}_N|_{[a,b]}\big\|_\infty > 2N^{-1/12}\big) \\&\qquad \leq \mathbb{P}\big(\mathcal{B}_2\cup\mathcal{B}_4^{-}\cup\mathcal{B}_4^+ \cup \big\{|I^{-}+(|x|+2\theta)N| \geq N^{3/4}\big\} \cup \big\{|I^+-(|x|+2\theta)N| \geq N^{3/4}\big\}\big), \end{align*}
which tends to 0 when N tends to
![]() $+\infty$
thanks to Lemmas 3, 7, and 11.
$+\infty$
thanks to Lemmas 3, 7, and 11.
Moreover, for any
![]() $-|x|-2\theta < a < b < |x|+2\theta$
, by Donsker’s invariance principle,
$-|x|-2\theta < a < b < |x|+2\theta$
, by Donsker’s invariance principle,
![]() $Y^{\prime}_N|_{[a,b]}$
converges in distribution to
$Y^{\prime}_N|_{[a,b]}$
converges in distribution to
![]() $B^x|_{[a,b]}$
when N tends to
$B^x|_{[a,b]}$
when N tends to
![]() $+\infty$
for the topology defined on D[a, b] by the uniform norm. The proof of Proposition 3 from this is standard, as was the proof of Theorem 2 from Lemmas 16 and 17.
$+\infty$
for the topology defined on D[a, b] by the uniform norm. The proof of Proposition 3 from this is standard, as was the proof of Theorem 2 from Lemmas 16 and 17.
6. No convergence in the Skorokhod
 $J_1$
topology: proof of Proposition 2
$J_1$
topology: proof of Proposition 2
In this section, our aim is to prove that
![]() $Y_N^\pm$
does not converge in distribution in the Skorokhod
$Y_N^\pm$
does not converge in distribution in the Skorokhod
![]() $J_1$
topology on
$J_1$
topology on
![]() $D({-}\infty,+\infty)$
when N tends to
$D({-}\infty,+\infty)$
when N tends to
![]() $+\infty$
. We will first prove that if
$+\infty$
. We will first prove that if
![]() $Y_N^\pm$
converges in the Skorokhod
$Y_N^\pm$
converges in the Skorokhod
![]() $J_1$
topology, then the limit has to be the same as in the Skorokhod
$J_1$
topology, then the limit has to be the same as in the Skorokhod
![]() $M_1$
topology, that is,
$M_1$
topology, that is,
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
, by Theorem 2 (this will be Lemma 22). Afterwards, we will prove that
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
, by Theorem 2 (this will be Lemma 22). Afterwards, we will prove that
![]() $Y_N^\pm$
does not converge in distribution in the Skorokhod
$Y_N^\pm$
does not converge in distribution in the Skorokhod
![]() $J_1$
topology to
$J_1$
topology to
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
, by finding some closed set
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
, by finding some closed set
![]() $\Xi$
such that
$\Xi$
such that
![]() $\limsup_{N\to+\infty}\mathbb{P}\big(Y_N^\pm \in \Xi\big) > \mathbb{P}\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}\in \Xi\big)$
, which is enough by the portmanteau theorem.
$\limsup_{N\to+\infty}\mathbb{P}\big(Y_N^\pm \in \Xi\big) > \mathbb{P}\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}\in \Xi\big)$
, which is enough by the portmanteau theorem.
Lemma 22.
If
![]() $Y_N^\pm$
converges in distribution in the Skorokhod
$Y_N^\pm$
converges in distribution in the Skorokhod
![]() $J_1$
topology on
$J_1$
topology on
![]() $D({-}\infty,+\infty)$
when N tends to
$D({-}\infty,+\infty)$
when N tends to
![]() $+\infty$
, the limit is
$+\infty$
, the limit is
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
.
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
.
Proof. The idea is that the Skorokhod
![]() $J_1$
topology is stronger than the Skorokhod
$J_1$
topology is stronger than the Skorokhod
![]() $M_1$
topology. We assume
$M_1$
topology. We assume
![]() $Y_N^\pm$
converges in distribution to some Z in the Skorokhod
$Y_N^\pm$
converges in distribution to some Z in the Skorokhod
![]() $J_1$
topology on
$J_1$
topology on
![]() $D({-}\infty,+\infty)$
when N tends to
$D({-}\infty,+\infty)$
when N tends to
![]() $+\infty$
. It can be proven that for any
$+\infty$
. It can be proven that for any
![]() $a>0$
we have
$a>0$
we have
![]() $d_{M_1,a} \leq d_{J_1,-a,a}$
. Indeed, this is Theorem 12.3.2 of [Reference Whitt19], whose proof is in the internet supplement of that book (just replace the points of discontinuity of
$d_{M_1,a} \leq d_{J_1,-a,a}$
. Indeed, this is Theorem 12.3.2 of [Reference Whitt19], whose proof is in the internet supplement of that book (just replace the points of discontinuity of
![]() $x_1$
with their image by
$x_1$
with their image by
![]() $\lambda^{-1}$
). This implies
$\lambda^{-1}$
). This implies
![]() $d_{M_1} \leq d_{J_1}$
. Therefore, a function
$d_{M_1} \leq d_{J_1}$
. Therefore, a function
![]() $g \,:\, D({-}\infty,+\infty) \mapsto \mathbb{R}$
that is bounded and continuous for the Skorokhod
$g \,:\, D({-}\infty,+\infty) \mapsto \mathbb{R}$
that is bounded and continuous for the Skorokhod
![]() $M_1$
topology is also continuous for the Skorokhod
$M_1$
topology is also continuous for the Skorokhod
![]() $J_1$
topology. We deduce that
$J_1$
topology. We deduce that
![]() $\mathbb{E}\big(g\big(Y_N^\pm\big)\big)$
converges to
$\mathbb{E}\big(g\big(Y_N^\pm\big)\big)$
converges to
![]() $\mathbb{E}(g(Z))$
when N tends to
$\mathbb{E}(g(Z))$
when N tends to
![]() $+\infty$
; thus
$+\infty$
; thus
![]() $Y_N^\pm$
converges in distribution to Z in the Skorokhod
$Y_N^\pm$
converges in distribution to Z in the Skorokhod
![]() $M_1$
topology when N tends to
$M_1$
topology when N tends to
![]() $+\infty$
. By Theorem 2, the limit has to be
$+\infty$
. By Theorem 2, the limit has to be
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
.
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
.
We now define our closed set
![]() $\Xi$
. The idea behind this definition is that with high probability,
$\Xi$
. The idea behind this definition is that with high probability,
![]() $B_{|x|+2\theta}^x$
is at some distance from 0; hence, at some point around
$B_{|x|+2\theta}^x$
is at some distance from 0; hence, at some point around
![]() $|x|+2\theta$
,
$|x|+2\theta$
,
![]() $Y_N^\pm$
will be close to
$Y_N^\pm$
will be close to
![]() $B_{|x|+2\theta}^x$
, and therefore at some distance from 0. Furthermore, at
$B_{|x|+2\theta}^x$
, and therefore at some distance from 0. Furthermore, at
![]() $|x|+2\theta$
the process
$|x|+2\theta$
the process
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
will jump directly from
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
will jump directly from
![]() $B_{|x|+2\theta}^x$
to 0, while
$B_{|x|+2\theta}^x$
to 0, while
![]() $Y_N^\pm$
, which can make only jumps of order
$Y_N^\pm$
, which can make only jumps of order
![]() $\frac{1}{\sqrt{N}}$
, will have to cross the distance separating
$\frac{1}{\sqrt{N}}$
, will have to cross the distance separating
![]() $B_{|x|+2\theta}^x$
from 0 without any big jumps. Therefore, if
$B_{|x|+2\theta}^x$
from 0 without any big jumps. Therefore, if
![]() $\delta_1>0$
is much smaller than
$\delta_1>0$
is much smaller than
![]() $B_{|x|+2\theta}^x$
, then
$B_{|x|+2\theta}^x$
, then
![]() $Y_N^\pm(y)$
will enter the interval
$Y_N^\pm(y)$
will enter the interval
![]() $[\delta_1,2\delta_1]$
for y near
$[\delta_1,2\delta_1]$
for y near
![]() $|x|+2\theta$
, while
$|x|+2\theta$
, while
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
will not. We thus set
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
will not. We thus set
![]() $\Xi$
to be roughly ‘the function enters
$\Xi$
to be roughly ‘the function enters
![]() $[\delta_1,2\delta_1]$
around
$[\delta_1,2\delta_1]$
around
![]() $|x|+2\theta$
’. More rigorously, by the definition of
$|x|+2\theta$
’. More rigorously, by the definition of
![]() $B^x$
, the random variable
$B^x$
, the random variable
![]() $B_{|x|+2\theta}^x$
has distribution
$B_{|x|+2\theta}^x$
has distribution
![]() $\mathcal{N}(0,2\theta)$
, which means there exists
$\mathcal{N}(0,2\theta)$
, which means there exists
![]() $\delta_1>0$
such that
$\delta_1>0$
such that
![]() $\mathbb{P}\big(\big|B_{|x|+2\theta}^x\big| \leq 4\delta_1\big) \leq 1/8$
. Moreover,
$\mathbb{P}\big(\big|B_{|x|+2\theta}^x\big| \leq 4\delta_1\big) \leq 1/8$
. Moreover,
![]() $B^x$
is continuous; hence there exists
$B^x$
is continuous; hence there exists
![]() $0 < \delta_2 <\theta$
such that
$0 < \delta_2 <\theta$
such that
![]() $\mathbb{P}\big(\exists\, y \in \big[|x|+2\theta-\delta_2,|x|+2\theta\big], \big|B_y^x\big| \leq 3\delta_1\big) \leq 1/4$
. We then define
$\mathbb{P}\big(\exists\, y \in \big[|x|+2\theta-\delta_2,|x|+2\theta\big], \big|B_y^x\big| \leq 3\delta_1\big) \leq 1/4$
. We then define
(the inclusion of
![]() $Z(y^{-})$
is necessary for
$Z(y^{-})$
is necessary for
![]() $\Xi$
to be closed). Then
$\Xi$
to be closed). Then
![]() $\mathbb{P}\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}} \in \Xi\big) \leq 1/4$
. We will prove the following two lemmas.
$\mathbb{P}\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}} \in \Xi\big) \leq 1/4$
. We will prove the following two lemmas.
Lemma 23.
When N is large enough,
![]() $\mathbb{P}\big(Y_N^\pm \in \Xi\big) \geq 1/2$
.
$\mathbb{P}\big(Y_N^\pm \in \Xi\big) \geq 1/2$
.
Lemma 24.
![]() $\Xi$
is closed in the Skorokhod
$\Xi$
is closed in the Skorokhod
![]() $J_1$
topology on
$J_1$
topology on
![]() $D({-}\infty,+\infty)$
.
$D({-}\infty,+\infty)$
.
With these two lemmas, the proof of Proposition 2 becomes easy.
Proof
of Proposition 2. Lemma 23 yields
![]() $\limsup_{N\to+\infty}\mathbb{P}\big(Y_N^\pm \in \Xi\big) \geq 1/2$
, and the definition of
$\limsup_{N\to+\infty}\mathbb{P}\big(Y_N^\pm \in \Xi\big) \geq 1/2$
, and the definition of
![]() $\Xi$
ensures that
$\Xi$
ensures that
![]() $\mathbb{P}\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}} \in \Xi\big) \leq 1/4$
; hence
$\mathbb{P}\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}} \in \Xi\big) \leq 1/4$
; hence
![]() $\limsup_{N\to+\infty}\mathbb{P}\big(Y_N^\pm \in \Xi\big) > \mathbb{P}\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}\in \Xi\big)$
. Since Lemma 24 yields that
$\limsup_{N\to+\infty}\mathbb{P}\big(Y_N^\pm \in \Xi\big) > \mathbb{P}\big(\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}\in \Xi\big)$
. Since Lemma 24 yields that
![]() $\Xi$
is closed in the Skorokhod
$\Xi$
is closed in the Skorokhod
![]() $J_1$
topology on
$J_1$
topology on
![]() $D({-}\infty,+\infty)$
, the portmanteau theorem implies that
$D({-}\infty,+\infty)$
, the portmanteau theorem implies that
![]() $Y_N^\pm$
does not converge in distribution in the Skorokhod
$Y_N^\pm$
does not converge in distribution in the Skorokhod
![]() $J_1$
topology on
$J_1$
topology on
![]() $D({-}\infty,+\infty)$
to
$D({-}\infty,+\infty)$
to
![]() $\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
when N tends to
$\big(B_y^x \mathbb{1}_{\{y\in[{-}|x|-2\theta,|x|+2\theta)\}}\big)_{y\in\mathbb{R}}$
when N tends to
![]() $+\infty$
. Hence Lemma 22 yields that
$+\infty$
. Hence Lemma 22 yields that
![]() $Y_N^\pm$
does not converge in distribution in the Skorokhod
$Y_N^\pm$
does not converge in distribution in the Skorokhod
![]() $J_1$
topology on
$J_1$
topology on
![]() $D({-}\infty,+\infty)$
when N tends to
$D({-}\infty,+\infty)$
when N tends to
![]() $+\infty$
, which is Proposition 2.
$+\infty$
, which is Proposition 2.
Thus it remains only to prove Lemmas 23 and 24.
Proof
of Lemma 23. The idea is that with good probability, when y is a bit smaller than
![]() $|x|+2\theta$
, we have that
$|x|+2\theta$
, we have that
![]() $Y_N^\pm(y)$
is of the same order as
$Y_N^\pm(y)$
is of the same order as
![]() $B_{|x|+2\theta}^x$
, and is thus away from 0, while when y is a bit larger than
$B_{|x|+2\theta}^x$
, and is thus away from 0, while when y is a bit larger than
![]() $|x|+2\theta$
, we have
$|x|+2\theta$
, we have
![]() $Y_N^\pm(y)=0$
, so, since
$Y_N^\pm(y)=0$
, so, since
![]() $Y_N$
can only make jumps of order
$Y_N$
can only make jumps of order
![]() $\frac{1}{\sqrt{N}}$
, it will enter
$\frac{1}{\sqrt{N}}$
, it will enter
![]() $[\delta_1,2\delta_1]$
.
$[\delta_1,2\delta_1]$
.
We now give the rigorous argument. We begin by assuming that
![]() $\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| > 3\delta_1$
(that is,
$\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| > 3\delta_1$
(that is,
![]() $Y_N(y)$
is indeed away from 0 when y is a bit smaller than
$Y_N(y)$
is indeed away from 0 when y is a bit smaller than
![]() $|x|+2\theta$
), that
$|x|+2\theta$
), that
![]() $(\mathcal{B}_2)^c$
occurs, and that
$(\mathcal{B}_2)^c$
occurs, and that
![]() $|I^+-(|x|+2\theta)N| < N^{3/4}$
; and we prove that when N is large enough,
$|I^+-(|x|+2\theta)N| < N^{3/4}$
; and we prove that when N is large enough,
![]() $Y_N^\pm \in \Xi$
. We first show that
$Y_N^\pm \in \Xi$
. We first show that
![]() $Y_N^\pm(|x|+2\theta+\delta_2)=0$
. When N is large enough,
$Y_N^\pm(|x|+2\theta+\delta_2)=0$
. When N is large enough,
![]() $\frac{I^+}{N} \leq |x|+2\theta+N^{-1/4} \leq |x|+2\theta+\delta_2$
. Moreover, Lemma 6 implies
$\frac{I^+}{N} \leq |x|+2\theta+N^{-1/4} \leq |x|+2\theta+\delta_2$
. Moreover, Lemma 6 implies
![]() $\ell^\pm\big(T_N,\lfloor Ny \rfloor\big)=0$
for any
$\ell^\pm\big(T_N,\lfloor Ny \rfloor\big)=0$
for any
![]() $y \geq \frac{I^+}{N}$
, and hence for
$y \geq \frac{I^+}{N}$
, and hence for
![]() $y=|x|+2\theta+\delta_2$
. This yields
$y=|x|+2\theta+\delta_2$
. This yields
![]() $Y_N^\pm(|x|+2\theta+\delta_2)=0$
. Moreover, we assumed
$Y_N^\pm(|x|+2\theta+\delta_2)=0$
. Moreover, we assumed
![]() $\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| > 3\delta_1$
. Equations (1) and (2) yield that the jumps of
$\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| > 3\delta_1$
. Equations (1) and (2) yield that the jumps of
![]() $Y_N^\pm$
in
$Y_N^\pm$
in
![]() $[|x|+2\theta-\delta_2,|x|+2\theta+\delta_2]$
are either
$[|x|+2\theta-\delta_2,|x|+2\theta+\delta_2]$
are either
![]() $\frac{1}{\sqrt{N}}\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)$
(if we are dealing with
$\frac{1}{\sqrt{N}}\eta_{i,+}\big(\ell^{-}\big(T_N,i\big)\big)$
(if we are dealing with
![]() $Y_N^{-}$
) or
$Y_N^{-}$
) or
![]() $\frac{1}{\sqrt{N}}\eta_{i+1,+}(\ell^{-}(T_N,i+1))$
(if we are dealing with
$\frac{1}{\sqrt{N}}\eta_{i+1,+}(\ell^{-}(T_N,i+1))$
(if we are dealing with
![]() $Y_N^+$
), with
$Y_N^+$
), with
![]() $i\in\{\lfloor(|x|+2\theta-\delta_2)N\rfloor,\ldots,\lfloor(|x|+2\theta+\delta_2)N\rfloor-1\}$
. Since
$i\in\{\lfloor(|x|+2\theta-\delta_2)N\rfloor,\ldots,\lfloor(|x|+2\theta+\delta_2)N\rfloor-1\}$
. Since
![]() $(\mathcal{B}_2)^c$
occurs, the jumps of
$(\mathcal{B}_2)^c$
occurs, the jumps of
![]() $Y_N^\pm$
in
$Y_N^\pm$
in
![]() $[|x|+2\theta-\delta_2,|x|+2\theta+\delta_2]$
have size at most
$[|x|+2\theta-\delta_2,|x|+2\theta+\delta_2]$
have size at most
![]() $\frac{1}{\sqrt{N}}\big(N^{1/16}+1/2\big)$
, which tends to 0 when N tends to
$\frac{1}{\sqrt{N}}\big(N^{1/16}+1/2\big)$
, which tends to 0 when N tends to
![]() $+\infty$
. Therefore, when N is large enough, there exists
$+\infty$
. Therefore, when N is large enough, there exists
![]() $y \in [|x|+2\theta-\delta_2,|x|+2\theta+\delta_2]$
such that
$y \in [|x|+2\theta-\delta_2,|x|+2\theta+\delta_2]$
such that
![]() $|Y_N^\pm(y)|\in[\delta_1,2\delta_1]$
; hence
$|Y_N^\pm(y)|\in[\delta_1,2\delta_1]$
; hence
![]() $Y_N^\pm\in\Xi$
. Consequently, when N is large enough, if
$Y_N^\pm\in\Xi$
. Consequently, when N is large enough, if
![]() $\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| > 3\delta_1$
,
$\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| > 3\delta_1$
,
![]() $(\mathcal{B}_2)^c$
, and
$(\mathcal{B}_2)^c$
, and
![]() $|I^+-(|x|+2\theta)N| < N^{3/4}$
then
$|I^+-(|x|+2\theta)N| < N^{3/4}$
then
![]() $Y_N^\pm\in\Xi$
. This implies that
$Y_N^\pm\in\Xi$
. This implies that
In addition, Lemma 3 and Lemma 7 yield respectively that
![]() $\mathbb{P}(\mathcal{B}_2)$
and
$\mathbb{P}(\mathcal{B}_2)$
and
![]() $\mathbb{P}\big(|I^+-(|x|+2\theta)N| \geq N^{3/4}\big)$
tend to 0 when N tends to
$\mathbb{P}\big(|I^+-(|x|+2\theta)N| \geq N^{3/4}\big)$
tend to 0 when N tends to
![]() $+\infty$
. Therefore, it is enough to prove that
$+\infty$
. Therefore, it is enough to prove that
![]() $\mathbb{P}\big(\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| \leq 3\delta_1\big) \leq 3/8$
when N is large enough to deduce that
$\mathbb{P}\big(\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| \leq 3\delta_1\big) \leq 3/8$
when N is large enough to deduce that
![]() $\mathbb{P}(Y_N^\pm \not\in \Xi) \leq 1/2$
when N is large enough and complete the proof of Lemma 23.
$\mathbb{P}(Y_N^\pm \not\in \Xi) \leq 1/2$
when N is large enough and complete the proof of Lemma 23.
We now prove that
![]() $\mathbb{P}\big(\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| \leq 3\delta_1\big) \leq 3/8$
when N is large enough, by noticing that
$\mathbb{P}\big(\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| \leq 3\delta_1\big) \leq 3/8$
when N is large enough, by noticing that
![]() $Y_N^\pm(|x|+2\theta-\delta_2)$
is close to
$Y_N^\pm(|x|+2\theta-\delta_2)$
is close to
![]() $Y^{\prime}_N(|x|+2\theta-\delta_2)$
, which will converge in distribution to
$Y^{\prime}_N(|x|+2\theta-\delta_2)$
, which will converge in distribution to
![]() $B_{|x|+2\theta-\delta_2}^x$
when N tends to
$B_{|x|+2\theta-\delta_2}^x$
when N tends to
![]() $+\infty$
. Lemma 21 implies that
$+\infty$
. Lemma 21 implies that
![]() $\mathbb{P}\big(\|Y_N^\pm|_{[0,|x|+2\theta-\delta_2]}-Y^{\prime}_N|_{[0,|x|+2\theta-\delta_2]}\|_\infty > 2N^{-1/12}\big)$
tends to 0 when N tends to
$\mathbb{P}\big(\|Y_N^\pm|_{[0,|x|+2\theta-\delta_2]}-Y^{\prime}_N|_{[0,|x|+2\theta-\delta_2]}\|_\infty > 2N^{-1/12}\big)$
tends to 0 when N tends to
![]() $+\infty$
; hence
$+\infty$
; hence
![]() $\mathbb{P}\big(\big|Y_N^\pm(|x|+2\theta-\delta_2)-Y^{\prime}_N(|x|+2\theta-\delta_2)\big| > 2N^{-1/12}\big)$
tends to 0 when N tends to
$\mathbb{P}\big(\big|Y_N^\pm(|x|+2\theta-\delta_2)-Y^{\prime}_N(|x|+2\theta-\delta_2)\big| > 2N^{-1/12}\big)$
tends to 0 when N tends to
![]() $+\infty$
, which implies
$+\infty$
, which implies
![]() $Y_N^\pm(|x|+2\theta-\delta_2)-Y^{\prime}_N(|x|+2\theta-\delta_2)$
converges in probability to 0 when N tends to
$Y_N^\pm(|x|+2\theta-\delta_2)-Y^{\prime}_N(|x|+2\theta-\delta_2)$
converges in probability to 0 when N tends to
![]() $+\infty$
. In addition, Lemma 18 states that
$+\infty$
. In addition, Lemma 18 states that
![]() $Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}$
converges in distribution to
$Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}$
converges in distribution to
![]() $B^x|_{[{-}|x|-2\theta,|x|+2\theta]}$
when N tends to
$B^x|_{[{-}|x|-2\theta,|x|+2\theta]}$
when N tends to
![]() $+\infty$
for the topology defined on
$+\infty$
for the topology defined on
![]() $C[{-}|x|-2\theta,|x|+2\theta]$
by the uniform norm; hence
$C[{-}|x|-2\theta,|x|+2\theta]$
by the uniform norm; hence
![]() $Y^{\prime}_N(|x|+2\theta-\delta_2)$
converges in distribution to
$Y^{\prime}_N(|x|+2\theta-\delta_2)$
converges in distribution to
![]() $B_{|x|+2\theta-\delta_2}^x$
when N tends to
$B_{|x|+2\theta-\delta_2}^x$
when N tends to
![]() $+\infty$
. Therefore, Slutsky’s theorem yields that
$+\infty$
. Therefore, Slutsky’s theorem yields that
![]() $Y_N^\pm(|x|+2\theta-\delta_2)$
converges in distribution to
$Y_N^\pm(|x|+2\theta-\delta_2)$
converges in distribution to
![]() $B_{|x|+2\theta-\delta_2}^x$
when N tends to
$B_{|x|+2\theta-\delta_2}^x$
when N tends to
![]() $+\infty$
. Moreover, we defined
$+\infty$
. Moreover, we defined
![]() $\Xi$
so that
$\Xi$
so that
![]() $\mathbb{P}(\exists\, y \in [|x|+2\theta-\delta_2,|x|+2\theta], |B_y^x| \leq 3\delta_1) \leq 1/4$
; hence
$\mathbb{P}(\exists\, y \in [|x|+2\theta-\delta_2,|x|+2\theta], |B_y^x| \leq 3\delta_1) \leq 1/4$
; hence
![]() $\mathbb{P}\big(\big|B_{|x|+2\theta-\delta_2}^x\big| \leq 3\delta_1\big) \leq 1/4$
. This implies that when N is large enough,
$\mathbb{P}\big(\big|B_{|x|+2\theta-\delta_2}^x\big| \leq 3\delta_1\big) \leq 1/4$
. This implies that when N is large enough,
![]() $\mathbb{P}\big(\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| \leq 3\delta_1\big) \leq 3/8$
.
$\mathbb{P}\big(\big|Y_N^\pm(|x|+2\theta-\delta_2)\big| \leq 3\delta_1\big) \leq 3/8$
.
Proof
of Lemma 24. Let
![]() $(Z_N)_{N\in\mathbb{N}}$
be a sequence of elements of
$(Z_N)_{N\in\mathbb{N}}$
be a sequence of elements of
![]() $\Xi$
converging to Z in the Skorokhod
$\Xi$
converging to Z in the Skorokhod
![]() $J_1$
topology on
$J_1$
topology on
![]() $D({-}\infty,+\infty)$
; we will prove that
$D({-}\infty,+\infty)$
; we will prove that
![]() $Z \in \Xi$
. By taking a subsequence, we may assume
$Z \in \Xi$
. By taking a subsequence, we may assume
![]() $d_{J_1}(Z,Z_N) < e^{-|x|-2\theta-\delta_2-1}/N$
for any
$d_{J_1}(Z,Z_N) < e^{-|x|-2\theta-\delta_2-1}/N$
for any
![]() $N\in\mathbb{N}^*$
. Then for any
$N\in\mathbb{N}^*$
. Then for any
![]() $N\in\mathbb{N}^*$
, some
$N\in\mathbb{N}^*$
, some
![]() $a_N > |x|+2\theta+\delta_2+1$
such that
$a_N > |x|+2\theta+\delta_2+1$
such that
![]() $d_{J_1,-a_N,a_N}\big(Z|_{[{-}a_N,a_N]},Z_N|_{[{-}a_N,a_N]}\big) \leq 1/N$
will exist. Indeed, if this were not the case, for some N we would have
$d_{J_1,-a_N,a_N}\big(Z|_{[{-}a_N,a_N]},Z_N|_{[{-}a_N,a_N]}\big) \leq 1/N$
will exist. Indeed, if this were not the case, for some N we would have
 \begin{align*} d_{J_1}(Z,Z_N)&=\int_0^{+\infty}e^{-a}\big(d_{J_1,-a,a}\big(Z|_{[{-}a,a]},Z_N|_{[{-}a,a]}\big) \wedge 1 \big)\mathrm{d}a \\ &\geq \int_{|x|+2\theta+\delta_2+1}^{+\infty}e^{-a}\frac{1}{N}\mathrm{d}a=e^{-|x|-2\theta-\delta_2-1}/N, \end{align*}
\begin{align*} d_{J_1}(Z,Z_N)&=\int_0^{+\infty}e^{-a}\big(d_{J_1,-a,a}\big(Z|_{[{-}a,a]},Z_N|_{[{-}a,a]}\big) \wedge 1 \big)\mathrm{d}a \\ &\geq \int_{|x|+2\theta+\delta_2+1}^{+\infty}e^{-a}\frac{1}{N}\mathrm{d}a=e^{-|x|-2\theta-\delta_2-1}/N, \end{align*}
which does not happen. For all
![]() $N\in \mathbb{N}^*$
, since
$N\in \mathbb{N}^*$
, since
![]() $d_{J_1,-a_N,a_N}\big(Z|_{[{-}a_N,a_N]},Z_N|_{[{-}a_N,a_N]}\big) \leq 1/N$
, there exists
$d_{J_1,-a_N,a_N}\big(Z|_{[{-}a_N,a_N]},Z_N|_{[{-}a_N,a_N]}\big) \leq 1/N$
, there exists
![]() $\lambda_N \in \Lambda_{-a_N,a_N}$
with
$\lambda_N \in \Lambda_{-a_N,a_N}$
with
![]() $\|Z|_{[{-}a_N,a_N]} \circ \lambda_N - Z_N|_{[{-}a_N,a_N]}\|_\infty\leq 2/N$
and
$\|Z|_{[{-}a_N,a_N]} \circ \lambda_N - Z_N|_{[{-}a_N,a_N]}\|_\infty\leq 2/N$
and
![]() $\|\lambda_N-\mathrm{Id}_{-a_N,a_N}\|_\infty \leq 2/N$
. Moreover,
$\|\lambda_N-\mathrm{Id}_{-a_N,a_N}\|_\infty \leq 2/N$
. Moreover,
![]() $Z_N\in\Xi$
; hence there exists
$Z_N\in\Xi$
; hence there exists
![]() $y_N \in [|x|+2\theta-\delta_2,|x|+2\theta+\delta_2]$
such that
$y_N \in [|x|+2\theta-\delta_2,|x|+2\theta+\delta_2]$
such that
![]() $|Z_N(y_N)|\in[\delta_1,2\delta_1]$
or
$|Z_N(y_N)|\in[\delta_1,2\delta_1]$
or
![]() $|Z_N\big(y_N^{-}\big)|\in[\delta_1,2\delta_1]$
. We now define
$|Z_N\big(y_N^{-}\big)|\in[\delta_1,2\delta_1]$
. We now define
![]() $y^{\prime}_N$
as follows: if
$y^{\prime}_N$
as follows: if
![]() $|Z_N(y_N)|\in[\delta_1,2\delta_1]$
we set
$|Z_N(y_N)|\in[\delta_1,2\delta_1]$
we set
![]() $y^{\prime}_N=y_N$
. Otherwise, since
$y^{\prime}_N=y_N$
. Otherwise, since
![]() $|Z_N\big(y_N^{-}\big)|\in[\delta_1,2\delta_1]$
, we can take some
$|Z_N\big(y_N^{-}\big)|\in[\delta_1,2\delta_1]$
, we can take some
![]() $y^{\prime}_N$
in
$y^{\prime}_N$
in
![]() $\big[y_N-\frac{1}{N},y_N\big]$
such that
$\big[y_N-\frac{1}{N},y_N\big]$
such that
![]() $\big|Z_N\big(y^{\prime}_N\big)\big|\in[\delta_1-1/N,2\delta_1+1/N]$
. In both cases, we have
$\big|Z_N\big(y^{\prime}_N\big)\big|\in[\delta_1-1/N,2\delta_1+1/N]$
. In both cases, we have
![]() $y^{\prime}_N \in [|x|+2\theta-\delta_2-1/N,|x|+2\theta+\delta_2]$
and
$y^{\prime}_N \in [|x|+2\theta-\delta_2-1/N,|x|+2\theta+\delta_2]$
and
![]() $\big|Z_N\big(y^{\prime}_N\big)\big|\in[\delta_1-1/N,2\delta_1+1/N]$
. Furthermore,
$\big|Z_N\big(y^{\prime}_N\big)\big|\in[\delta_1-1/N,2\delta_1+1/N]$
. Furthermore,
![]() $\|\lambda_N-\mathrm{Id}_{-a_N,a_N}\|_\infty \leq 2/N$
; hence
$\|\lambda_N-\mathrm{Id}_{-a_N,a_N}\|_\infty \leq 2/N$
; hence
![]() $|\lambda_N\big(y^{\prime}_N\big)-y^{\prime}_N| \leq 2/N$
, and thus
$|\lambda_N\big(y^{\prime}_N\big)-y^{\prime}_N| \leq 2/N$
, and thus
![]() $\lambda_N\big(y^{\prime}_N\big) \in [|x|+2\theta-\delta_2-3/N,|x|+2\theta+\delta_2+2/N]$
. In addition,
$\lambda_N\big(y^{\prime}_N\big) \in [|x|+2\theta-\delta_2-3/N,|x|+2\theta+\delta_2+2/N]$
. In addition,
![]() $\big\|Z\big(\lambda_N\big(y^{\prime}_N\big)\big) - Z_N\big(y^{\prime}_N\big)\big\|_\infty\leq 2/N$
; hence
$\big\|Z\big(\lambda_N\big(y^{\prime}_N\big)\big) - Z_N\big(y^{\prime}_N\big)\big\|_\infty\leq 2/N$
; hence
![]() $\big|Z\big(\lambda_N\big(y^{\prime}_N\big)\big)\big|\in[\delta_1-3/N,2\delta_1+3/N]$
. By taking a subsequence, we may assume that
$\big|Z\big(\lambda_N\big(y^{\prime}_N\big)\big)\big|\in[\delta_1-3/N,2\delta_1+3/N]$
. By taking a subsequence, we may assume that
![]() $\lambda_N\big(y^{\prime}_N\big)$
converges to some
$\lambda_N\big(y^{\prime}_N\big)$
converges to some
![]() $y_\infty\in [|x|+2\theta-\delta_2,|x|+2\theta+\delta_2]$
. In addition, Z is càdlàg, so there is a subsequence of
$y_\infty\in [|x|+2\theta-\delta_2,|x|+2\theta+\delta_2]$
. In addition, Z is càdlàg, so there is a subsequence of
![]() $\big(Z\big(\lambda_N\big(y^{\prime}_N\big)\big)_{N\in\mathbb{N}^*}$
that converges to either
$\big(Z\big(\lambda_N\big(y^{\prime}_N\big)\big)_{N\in\mathbb{N}^*}$
that converges to either
![]() $Z(y_\infty)$
or
$Z(y_\infty)$
or
![]() $Z\big(y_\infty^{-}\big)$
. Since
$Z\big(y_\infty^{-}\big)$
. Since
![]() $\big|Z\big(\lambda_N\big(y^{\prime}_N\big)\big)\big|\in[\delta_1-3/N,2\delta_1+3/N]$
, we have
$\big|Z\big(\lambda_N\big(y^{\prime}_N\big)\big)\big|\in[\delta_1-3/N,2\delta_1+3/N]$
, we have
![]() $|Z(y_\infty)|$
or
$|Z(y_\infty)|$
or
![]() $\big|Z\big(y_\infty^{-}\big)\big|$
in
$\big|Z\big(y_\infty^{-}\big)\big|$
in
![]() $[\delta_1,2\delta_1]$
. Therefore
$[\delta_1,2\delta_1]$
. Therefore
![]() $Z\in \Xi$
, which completes the proof.
$Z\in \Xi$
, which completes the proof.
7. Convergence of the stopping time: proof of Proposition 4
We want to prove Proposition 4, that is, the convergence in distribution of
![]() $\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)$
to the law
$\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)$
to the law
![]() $\mathcal{N}\big(0,\frac{32}{3}\mathrm{Var}(\rho_-)\big((|x|+\theta)^3+\theta^3\big)\big)$
when N tends to
$\mathcal{N}\big(0,\frac{32}{3}\mathrm{Var}(\rho_-)\big((|x|+\theta)^3+\theta^3\big)\big)$
when N tends to
![]() $+\infty$
. In order to do that, we will prove that
$+\infty$
. In order to do that, we will prove that
![]() $\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)$
is close to
$\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)$
is close to
![]() $2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
(where
$2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
(where
![]() $Y^{\prime}_N$
was defined at the beginning of Section 5.1), then that
$Y^{\prime}_N$
was defined at the beginning of Section 5.1), then that
![]() $2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges to the desired distribution.
$2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges to the desired distribution.
Proposition 7. We have that
 \begin{equation*}\mathbb{P}\left( \left|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)-2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y \right| > 5(|x|+2\theta)N^{-1/12}\right)\end{equation*}
\begin{equation*}\mathbb{P}\left( \left|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)-2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y \right| > 5(|x|+2\theta)N^{-1/12}\right)\end{equation*}
tends to 0 when N tends to
![]() $+\infty$
.
$+\infty$
.
Proof. The result will come from the fact that
![]() $T_N$
can be written as the sum of the local times, which is itself related to the integrals of
$T_N$
can be written as the sum of the local times, which is itself related to the integrals of
![]() $Y_N^{-}$
and
$Y_N^{-}$
and
![]() $Y_N^+$
, which are close to
$Y_N^+$
, which are close to
![]() $Y_N$
by Lemma 12 and hence to
$Y_N$
by Lemma 12 and hence to
![]() $Y^{\prime}_N$
by Lemma 19. It is enough to prove that if
$Y^{\prime}_N$
by Lemma 19. It is enough to prove that if
![]() $(\mathcal{B}_2)^c$
,
$(\mathcal{B}_2)^c$
,
![]() $\big(\mathcal{B}_4^{-}\big)^c$
, and
$\big(\mathcal{B}_4^{-}\big)^c$
, and
![]() $\big(\mathcal{B}_4^+\big)^c$
occur and if
$\big(\mathcal{B}_4^+\big)^c$
occur and if
![]() $|I^{-}+(|x|+2\theta)N| < N^{5/8}$
,
$|I^{-}+(|x|+2\theta)N| < N^{5/8}$
,
![]() $|I^+-(|x|+2\theta)N| < N^{5/8}$
, then
$|I^+-(|x|+2\theta)N| < N^{5/8}$
, then
 \begin{equation*}\left|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)-2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y \right| \leq 5(|x|+2\theta)N^{-1/12},\end{equation*}
\begin{equation*}\left|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)-2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y \right| \leq 5(|x|+2\theta)N^{-1/12},\end{equation*}
since Lemma 3 implies that
![]() $\mathbb{P}(\mathcal{B}_2)$
tends to 0 when N tends to
$\mathbb{P}(\mathcal{B}_2)$
tends to 0 when N tends to
![]() $+\infty$
, Lemma 11 implies that
$+\infty$
, Lemma 11 implies that
![]() $\mathbb{P}\big(\mathcal{B}_4^{-}\big)$
and
$\mathbb{P}\big(\mathcal{B}_4^{-}\big)$
and
![]() $\mathbb{P}\big(\mathcal{B}_4^+\big)$
tend to 0 when N tends to
$\mathbb{P}\big(\mathcal{B}_4^+\big)$
tend to 0 when N tends to
![]() $+\infty$
, and Lemma 7 implies that
$+\infty$
, and Lemma 7 implies that
![]() $\mathbb{P}\big(|I^{-}+(|x|+2\theta)N| \geq N^{5/8}\big)$
and
$\mathbb{P}\big(|I^{-}+(|x|+2\theta)N| \geq N^{5/8}\big)$
and
![]() $\mathbb{P}\big(|I^+-(|x|+2\theta)N| \geq N^{5/8}\big)$
tend to 0 when N tends to
$\mathbb{P}\big(|I^+-(|x|+2\theta)N| \geq N^{5/8}\big)$
tend to 0 when N tends to
![]() $+\infty$
. We assume that
$+\infty$
. We assume that
![]() $(\mathcal{B}_2)^c$
,
$(\mathcal{B}_2)^c$
,
![]() $\big(\mathcal{B}_4^{-}\big)^c$
, and
$\big(\mathcal{B}_4^{-}\big)^c$
, and
![]() $\big(\mathcal{B}_4^+\big)^c$
occur and that
$\big(\mathcal{B}_4^+\big)^c$
occur and that
![]() $|I^{-}+(|x|+2\theta)N| < N^{5/8}$
,
$|I^{-}+(|x|+2\theta)N| < N^{5/8}$
,
![]() $|I^+-(|x|+2\theta)N| < N^{5/8}$
. Let us study
$|I^+-(|x|+2\theta)N| < N^{5/8}$
. Let us study
![]() $T_N$
.
$T_N$
.
In order to do this, we first need to prove an auxiliary result—more precisely, that the following holds when N is large enough:
We prove (6) for the case
![]() $|i-I^{-}| \leq N^{5/8}+1$
, since the other case is similar. Let
$|i-I^{-}| \leq N^{5/8}+1$
, since the other case is similar. Let
![]() $i \in \mathbb{Z}$
so that
$i \in \mathbb{Z}$
so that
![]() $|i-I^{-}| < N^{5/8}+1$
. We notice that since
$|i-I^{-}| < N^{5/8}+1$
. We notice that since
![]() $|I^{-}+(|x|+2\theta)N| < N^{5/8}$
we have
$|I^{-}+(|x|+2\theta)N| < N^{5/8}$
we have
![]() $I^{-},i < 0$
when N is large enough, so (1) yields
$I^{-},i < 0$
when N is large enough, so (1) yields
thus, since
![]() $\ell^+(T_N,I^{-})=0$
, we have
$\ell^+(T_N,I^{-})=0$
, we have
In addition, we assumed
![]() $(\mathcal{B}_2)^c$
; hence
$(\mathcal{B}_2)^c$
; hence
when N is large enough. Furthermore, (2) implies
thanks to
![]() $(\mathcal{B}_2)^c$
, and hence
$(\mathcal{B}_2)^c$
, and hence
![]() $\ell^{-}(T_N,i) \leq 3N^{11/16}+N^{1/16}+1/2 \leq 4 N^{11/16}$
when N is large enough, which completes the proof of (6).
$\ell^{-}(T_N,i) \leq 3N^{11/16}+N^{1/16}+1/2 \leq 4 N^{11/16}$
when N is large enough, which completes the proof of (6).
We now write
![]() $T_N$
as the sum of the local times and relate
$T_N$
as the sum of the local times and relate
![]() $\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)$
to the integral of
$\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)$
to the integral of
![]() $Y^+$
and
$Y^+$
and
![]() $Y^{-}$
. We have
$Y^{-}$
. We have
![]() $T_N = \sum_{i\in\mathbb{Z}}(\ell^+(T_N,i)+\ell^{-}(T_N,i))$
. Moreover, Lemma 6 implies that for all
$T_N = \sum_{i\in\mathbb{Z}}(\ell^+(T_N,i)+\ell^{-}(T_N,i))$
. Moreover, Lemma 6 implies that for all
![]() $i \geq I^+$
and
$i \geq I^+$
and
![]() $i \leq I^{-}$
we have
$i \leq I^{-}$
we have
![]() $\ell^+(T_N,i)=\ell^{-}(T_N,i)=0$
. Consequently,
$\ell^+(T_N,i)=\ell^{-}(T_N,i)=0$
. Consequently,
 \begin{equation*}T_N = \sum_{i=I^{-} \wedge ({-}\lfloor (|x|+2\theta)N\rfloor)}^{I^+ \vee \lfloor (|x|+2\theta)N\rfloor}\big(\ell^+(T_N,i)+\ell^{-}(T_N,i)\big).\end{equation*}
\begin{equation*}T_N = \sum_{i=I^{-} \wedge ({-}\lfloor (|x|+2\theta)N\rfloor)}^{I^+ \vee \lfloor (|x|+2\theta)N\rfloor}\big(\ell^+(T_N,i)+\ell^{-}(T_N,i)\big).\end{equation*}
We thus have
 \begin{align*} &\left|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)-\int_{(I^{-}\wedge ({-}(|x|+2\theta)N))/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y \right|\\&\qquad \leq \frac{1}{N^{3/2}}\big(\ell^+\big(T_N,I^+ \vee \lfloor (|x|+2\theta)N\rfloor\big)+\ell^{-}\big(T_N,I^+ \vee \lfloor (|x|+2\theta)N\rfloor\big)\\&\qquad \quad +\ell^+\big(T_N,-\lfloor (|x|+2\theta)N\rfloor-1\big)+\ell^{-}\big(T_N,-\lfloor (|x|+2\theta)N\rfloor-1\big)\big). \end{align*}
\begin{align*} &\left|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)-\int_{(I^{-}\wedge ({-}(|x|+2\theta)N))/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y \right|\\&\qquad \leq \frac{1}{N^{3/2}}\big(\ell^+\big(T_N,I^+ \vee \lfloor (|x|+2\theta)N\rfloor\big)+\ell^{-}\big(T_N,I^+ \vee \lfloor (|x|+2\theta)N\rfloor\big)\\&\qquad \quad +\ell^+\big(T_N,-\lfloor (|x|+2\theta)N\rfloor-1\big)+\ell^{-}\big(T_N,-\lfloor (|x|+2\theta)N\rfloor-1\big)\big). \end{align*}
Since we assumed
![]() $|I^{-}+(|x|+2\theta)N| < N^{5/8}$
and
$|I^{-}+(|x|+2\theta)N| < N^{5/8}$
and
![]() $|I^+-(|x|+2\theta)N| < N^{5/8}$
, Equation (6) yields
$|I^+-(|x|+2\theta)N| < N^{5/8}$
, Equation (6) yields
 \begin{equation} \begin{split} \left|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)-\int_{(I^{-}\wedge ({-}(|x|+2\theta)N))/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y\right| \\ \leq \frac{1}{N^{3/2}}16 N^{11/16}=16N^{-13/16}.\qquad\qquad\qquad\qquad \end{split} \end{equation}
\begin{equation} \begin{split} \left|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)-\int_{(I^{-}\wedge ({-}(|x|+2\theta)N))/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y\right| \\ \leq \frac{1}{N^{3/2}}16 N^{11/16}=16N^{-13/16}.\qquad\qquad\qquad\qquad \end{split} \end{equation}
We now prove that
is close to
![]() $2\int_{-(|x|+2\theta)}^{|x|+2\theta}Y_N(y)\mathrm{d}y$
. We begin by considering
$2\int_{-(|x|+2\theta)}^{|x|+2\theta}Y_N(y)\mathrm{d}y$
. We begin by considering
We first assume
![]() $I^+ \geq (|x|+2\theta)N$
. Since we assumed that
$I^+ \geq (|x|+2\theta)N$
. Since we assumed that
![]() $(\mathcal{B}_2)^c$
,
$(\mathcal{B}_2)^c$
,
![]() $\big(\mathcal{B}_4^{-}\big)^c$
, and
$\big(\mathcal{B}_4^{-}\big)^c$
, and
![]() $\big(\mathcal{B}_4^+\big)^c$
occur, Lemma 12 yields
$\big(\mathcal{B}_4^+\big)^c$
occur, Lemma 12 yields
 \begin{align*} &\left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y \right| \\ &\qquad \leq 2\left(|x|+2\theta-\frac{\chi(N)}{N}\right)N^{-1/12}+\int_{|x|+2\theta}^{I^+/N}|Y_N^+(y)+Y_N^{-}(y))|\mathrm{d}y. \end{align*}
\begin{align*} &\left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y \right| \\ &\qquad \leq 2\left(|x|+2\theta-\frac{\chi(N)}{N}\right)N^{-1/12}+\int_{|x|+2\theta}^{I^+/N}|Y_N^+(y)+Y_N^{-}(y))|\mathrm{d}y. \end{align*}
In addition, we know
![]() $I^+ - (|x|+2\theta)N \leq N^{5/8}$
and (6); hence
$I^+ - (|x|+2\theta)N \leq N^{5/8}$
and (6); hence
We deduce that
 \begin{equation*} \left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y\right| \end{equation*}
\begin{equation*} \left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y\right| \end{equation*}
We now assume
![]() $I^+ < (|x|+2\theta)N$
. In this case, we have
$I^+ < (|x|+2\theta)N$
. In this case, we have
 \begin{equation*} \left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y\right| \end{equation*}
\begin{equation*} \left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y\right| \end{equation*}
Moreover, Lemma 12 yields
Furthermore, for
![]() $y \geq \frac{I^+}{N}$
we have
$y \geq \frac{I^+}{N}$
we have
![]() $\ell^\pm\big(T_N,\lfloor Ny\rfloor\big)=0$
. Since
$\ell^\pm\big(T_N,\lfloor Ny\rfloor\big)=0$
. Since
![]() $|I^+ - (|x|+2\theta)N| < N^{5/8}$
, this yields
$|I^+ - (|x|+2\theta)N| < N^{5/8}$
, this yields
![]() $\big|Y_N^\pm(y)\big| \leq \frac{1}{2}N^{1/8}$
. Thus
$\big|Y_N^\pm(y)\big| \leq \frac{1}{2}N^{1/8}$
. Thus
We deduce that
 \begin{equation*} \left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y\right| \end{equation*}
\begin{equation*} \left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y\right| \end{equation*}
In addition, for any
![]() $y\in[\frac{I^+}{N},|x|+2\theta]$
, we have
$y\in[\frac{I^+}{N},|x|+2\theta]$
, we have
Lemma 12 yields that
![]() $\left|Y_N\left(\frac{I^+}{N} \right)-Y_N^{-}\left(\frac{I^+}{N} \right)\right| \leq N^{-1/12}$
, and since
$\left|Y_N\left(\frac{I^+}{N} \right)-Y_N^{-}\left(\frac{I^+}{N} \right)\right| \leq N^{-1/12}$
, and since
![]() $|I^+ - (|x|+2\theta)N| < N^{5/8}$
we have
$|I^+ - (|x|+2\theta)N| < N^{5/8}$
we have
hence
 \begin{equation*}|Y_N(y)| \leq \left|Y_N(y)-Y_N\left(\frac{I^+}{N}\right)\right|+N^{-1/12}+\frac{1}{2}N^{1/8}=\frac{1}{\sqrt{N}}\left|\sum_{i=I^+}^{\lfloor Ny\rfloor-1}\zeta_i\right|+N^{-1/12}+\frac{1}{2}N^{1/8}\end{equation*}
\begin{equation*}|Y_N(y)| \leq \left|Y_N(y)-Y_N\left(\frac{I^+}{N}\right)\right|+N^{-1/12}+\frac{1}{2}N^{1/8}=\frac{1}{\sqrt{N}}\left|\sum_{i=I^+}^{\lfloor Ny\rfloor-1}\zeta_i\right|+N^{-1/12}+\frac{1}{2}N^{1/8}\end{equation*}
 \begin{equation*}\leq \frac{1}{\sqrt{N}}\sum_{i=I^+}^{\lfloor (|x|+2\theta)N\rfloor-1}|\zeta_i|+N^{-1/12}+\frac{1}{2}N^{1/8} \leq \frac{1}{\sqrt{N}}N^{5/8}N^{1/16}+N^{-1/12}+\frac{1}{2}N^{1/8} \leq 2N^{3/16}\end{equation*}
\begin{equation*}\leq \frac{1}{\sqrt{N}}\sum_{i=I^+}^{\lfloor (|x|+2\theta)N\rfloor-1}|\zeta_i|+N^{-1/12}+\frac{1}{2}N^{1/8} \leq \frac{1}{\sqrt{N}}N^{5/8}N^{1/16}+N^{-1/12}+\frac{1}{2}N^{1/8} \leq 2N^{3/16}\end{equation*}
since
![]() $(\mathcal{B}_2)^c$
occurs. Thus
$(\mathcal{B}_2)^c$
occurs. Thus
We deduce that
 \begin{align*}&\left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y \right| \\&\qquad \leq 2\left(|x|+2\theta-\frac{\chi(N)}{N}\right)N^{-1/12}+5N^{-3/16}.\end{align*}
\begin{align*}&\left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y \right| \\&\qquad \leq 2\left(|x|+2\theta-\frac{\chi(N)}{N}\right)N^{-1/12}+5N^{-3/16}.\end{align*}
Consequently, in all cases,
 \begin{align*}&\left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y \right| \\&\qquad \leq 2\left(|x|+2\theta-\frac{\chi(N)}{N}\right)N^{-1/12}+8N^{-3/16}.\end{align*}
\begin{align*}&\left|\int_{\chi(N)/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{\chi(N)/N}^{|x|+2\theta}Y_N(y)\mathrm{d}y \right| \\&\qquad \leq 2\left(|x|+2\theta-\frac{\chi(N)}{N}\right)N^{-1/12}+8N^{-3/16}.\end{align*}
One can prove similarly that
 \begin{align*}&\left|\int_{(I^{-}\wedge ({-}(|x|+2\theta)N))/N}^{\chi(N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{-(|x|+2\theta)}^{\chi(N)/N}Y_N(y)\mathrm{d}y \right| \\&\qquad \leq 2\left(|x|+2\theta+\frac{\chi(N)}{N}\right)N^{-1/12}+8N^{-3/16}.\end{align*}
\begin{align*}&\left|\int_{(I^{-}\wedge ({-}(|x|+2\theta)N))/N}^{\chi(N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{-(|x|+2\theta)}^{\chi(N)/N}Y_N(y)\mathrm{d}y \right| \\&\qquad \leq 2\left(|x|+2\theta+\frac{\chi(N)}{N}\right)N^{-1/12}+8N^{-3/16}.\end{align*}
We conclude that
 \begin{align*}&\left|\int_{(I^{-}\wedge ({-}(|x|+2\theta)N))/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{-(|x|+2\theta)}^{|x|+2\theta}Y_N(y)\mathrm{d}y \right| \\& \qquad \leq 4(|x|+2\theta)N^{-1/12}+16N^{-3/16}.\end{align*}
\begin{align*}&\left|\int_{(I^{-}\wedge ({-}(|x|+2\theta)N))/N}^{(I^+\vee (|x|+2\theta)N)/N}\big(Y_N^+(y)+Y_N^{-}(y)\big)\mathrm{d}y-2\int_{-(|x|+2\theta)}^{|x|+2\theta}Y_N(y)\mathrm{d}y \right| \\& \qquad \leq 4(|x|+2\theta)N^{-1/12}+16N^{-3/16}.\end{align*}
We are now in position to conclude. Indeed, the previous result and (7) imply that when N is large enough,
![]() $|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)- 2\int_{-(|x|+2\theta)}^{|x|+2\theta}Y_N(y)\mathrm{d}y| \leq 16N^{-13/16}+4(|x|+2\theta)N^{-1/12}+16N^{-3/16}$
. Moreover,
$|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)- 2\int_{-(|x|+2\theta)}^{|x|+2\theta}Y_N(y)\mathrm{d}y| \leq 16N^{-13/16}+4(|x|+2\theta)N^{-1/12}+16N^{-3/16}$
. Moreover,
![]() $(\mathcal{B}_2)^c$
occurs, so Lemma 19 yields
$(\mathcal{B}_2)^c$
occurs, so Lemma 19 yields
![]() $\sup\{\big|Y_N(y)-Y^{\prime}_N(y)\big|\,:\,y\in[{-}|x|-2\theta,|x|+2\theta)\} \leq N^{-7/16}$
; therefore
$\sup\{\big|Y_N(y)-Y^{\prime}_N(y)\big|\,:\,y\in[{-}|x|-2\theta,|x|+2\theta)\} \leq N^{-7/16}$
; therefore
 \begin{equation*}\left|\int_{-(|x|+2\theta)}^{|x|+2\theta}Y_N(y)\mathrm{d}y-\int_{-(|x|+2\theta)}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y \right| \leq 2(|x|+2\theta)N^{-7/16}.\end{equation*}
\begin{equation*}\left|\int_{-(|x|+2\theta)}^{|x|+2\theta}Y_N(y)\mathrm{d}y-\int_{-(|x|+2\theta)}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y \right| \leq 2(|x|+2\theta)N^{-7/16}.\end{equation*}
We deduce that when N is large enough,
 \begin{align*}&\left|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)- 2\int_{-(|x|+2\theta)}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y\right|\\& \qquad \leq 16N^{-13/16}+4(|x|+2\theta)N^{-1/12}+16N^{-3/16}+4(|x|+2\theta)N^{-7/16}\\& \qquad \leq 5(|x|+2\theta)N^{-1/12},\end{align*}
\begin{align*}&\left|\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)- 2\int_{-(|x|+2\theta)}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y\right|\\& \qquad \leq 16N^{-13/16}+4(|x|+2\theta)N^{-1/12}+16N^{-3/16}+4(|x|+2\theta)N^{-7/16}\\& \qquad \leq 5(|x|+2\theta)N^{-1/12},\end{align*}
which completes the proof.
Now that we know
![]() $\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)$
is close to
$\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)$
is close to
![]() $2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
, we need to prove that
$2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
, we need to prove that
![]() $2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges to the desired distribution. In order to do so, we will use the convergence of
$2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges to the desired distribution. In order to do so, we will use the convergence of
![]() $Y^{\prime}_N$
to a Brownian motion as stated in Lemma 18; thus
$Y^{\prime}_N$
to a Brownian motion as stated in Lemma 18; thus
![]() $2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
will converge to the integral of a Brownian motion. The law of the latter is characterized by the following lemma, where we denote by
$2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
will converge to the integral of a Brownian motion. The law of the latter is characterized by the following lemma, where we denote by
![]() $(B_t)_{t\in\mathbb{R}^+}$
a standard Brownian motion with
$(B_t)_{t\in\mathbb{R}^+}$
a standard Brownian motion with
![]() $B_0=0$
. This lemma is quite standard (the interested reader can find a proof in the first arXiv version of this paper [Reference Marêché5]).
$B_0=0$
. This lemma is quite standard (the interested reader can find a proof in the first arXiv version of this paper [Reference Marêché5]).
Lemma 25.
For any
![]() $y>0$
, the integral
$y>0$
, the integral
![]() $\int_0^y B_{z} \mathrm{d}z$
has distribution
$\int_0^y B_{z} \mathrm{d}z$
has distribution
![]() $\mathcal{N}\Big(0,\frac{y^3}{3}\Big)$
.
$\mathcal{N}\Big(0,\frac{y^3}{3}\Big)$
.
We are now able to prove Proposition 4.
Proof
of Proposition 4. Proposition 7 implies that the quantity
![]() $\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)-2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges in probability to 0 when N tends to
$\frac{1}{N^{3/2}}\big(T_N-N^2(|x|+2\theta)^2\big)-2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges in probability to 0 when N tends to
![]() $+\infty$
. Hence, by Slutsky’s theorem, to prove Proposition 4, it is enough to prove that
$+\infty$
. Hence, by Slutsky’s theorem, to prove Proposition 4, it is enough to prove that
![]() $2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges in distribution to
$2\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges in distribution to
![]() $\mathcal{N}\big(0,\mathrm{Var}(\rho_-)\frac{32}{3}\big((|x|+\theta)^3+\theta^3\big)\big)$
when N tends to
$\mathcal{N}\big(0,\mathrm{Var}(\rho_-)\frac{32}{3}\big((|x|+\theta)^3+\theta^3\big)\big)$
when N tends to
![]() $+\infty$
. In addition, by Lemma 18,
$+\infty$
. In addition, by Lemma 18,
![]() $Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}$
converges in distribution to
$Y^{\prime}_N|_{[{-}|x|-2\theta,|x|+2\theta]}$
converges in distribution to
![]() $B^x|_{[{-}|x|-2\theta,|x|+2\theta]}$
when N tends to
$B^x|_{[{-}|x|-2\theta,|x|+2\theta]}$
when N tends to
![]() $+\infty$
, for the topology defined on
$+\infty$
, for the topology defined on
![]() $C[{-}|x|-2\theta,|x|+2\theta]$
by the uniform norm. The integral between
$C[{-}|x|-2\theta,|x|+2\theta]$
by the uniform norm. The integral between
![]() $-|x|-2\theta$
and
$-|x|-2\theta$
and
![]() $|x|+2\theta$
is continuous for this topology, so
$|x|+2\theta$
is continuous for this topology, so
![]() $\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges in distribution to
$\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges in distribution to
![]() $\int_{-|x|-2\theta}^{|x|+2\theta}B_y^x\mathrm{d}y$
when N tends to
$\int_{-|x|-2\theta}^{|x|+2\theta}B_y^x\mathrm{d}y$
when N tends to
![]() $+\infty$
. Furthermore,
$+\infty$
. Furthermore,
![]() $B^x$
is a two-sided Brownian motion with
$B^x$
is a two-sided Brownian motion with
![]() $B_x^x=0$
and variance
$B_x^x=0$
and variance
![]() $\mathrm{Var}(\rho_-)$
, which means we can write
$\mathrm{Var}(\rho_-)$
, which means we can write
where
![]() $\int_{-|x|-2\theta}^{x}B_y^x\mathrm{d}y$
and
$\int_{-|x|-2\theta}^{x}B_y^x\mathrm{d}y$
and
![]() $\int_{x}^{|x|+2\theta}B_y^x\mathrm{d}y$
are independent. In addition,
$\int_{x}^{|x|+2\theta}B_y^x\mathrm{d}y$
are independent. In addition,
![]() $\int_{x}^{|x|+2\theta}B_y^x\mathrm{d}y$
has the distribution of
$\int_{x}^{|x|+2\theta}B_y^x\mathrm{d}y$
has the distribution of
![]() $\sqrt{\mathrm{Var}(\rho_-)}\int_{0}^{2\theta}B_y\mathrm{d}y$
, which we know is
$\sqrt{\mathrm{Var}(\rho_-)}\int_{0}^{2\theta}B_y\mathrm{d}y$
, which we know is
![]() $\mathcal{N}\Big(0,\mathrm{Var}(\rho_-)\frac{(2\theta)^3}{3}\Big)$
by Lemma 25, and
$\mathcal{N}\Big(0,\mathrm{Var}(\rho_-)\frac{(2\theta)^3}{3}\Big)$
by Lemma 25, and
![]() $\int_{-|x|-2\theta}^x B_y^x\mathrm{d}y$
has the distribution of
$\int_{-|x|-2\theta}^x B_y^x\mathrm{d}y$
has the distribution of
![]() $\sqrt{\mathrm{Var}(\rho_-)}\int_{0}^{2|x|+2\theta}B_y\mathrm{d}y$
, which is
$\sqrt{\mathrm{Var}(\rho_-)}\int_{0}^{2|x|+2\theta}B_y\mathrm{d}y$
, which is
![]() $\mathcal{N}\Big(0,\mathrm{Var}(\rho_-)\frac{(2|x|+2\theta)^3}{3}\Big)$
by Lemma 25. We obtain that
$\mathcal{N}\Big(0,\mathrm{Var}(\rho_-)\frac{(2|x|+2\theta)^3}{3}\Big)$
by Lemma 25. We obtain that
![]() $\int_{-|x|-2\theta}^{|x|+2\theta}B_y^x\mathrm{d}y$
has the distribution
$\int_{-|x|-2\theta}^{|x|+2\theta}B_y^x\mathrm{d}y$
has the distribution
Consequently,
![]() $\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges in distribution to
$\int_{-|x|-2\theta}^{|x|+2\theta}Y^{\prime}_N(y)\mathrm{d}y$
converges in distribution to
![]() $\mathcal{N}\big(0,\mathrm{Var}(\rho_-)\frac{8}{3}\big((|x|+\theta)^3+\theta^3\big)\big)$
when N tends to
$\mathcal{N}\big(0,\mathrm{Var}(\rho_-)\frac{8}{3}\big((|x|+\theta)^3+\theta^3\big)\big)$
when N tends to
![]() $+\infty$
, which completes the proof of Proposition 4.
$+\infty$
, which completes the proof of Proposition 4.
Acknowledgement
The author wishes to thank Thomas Mountford for introducing her to this random walk and pointing her to some references.
Funding information
The author was supported by the University of Strasbourg Initiative of Excellence.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.