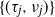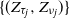1. Introduction
Branching processes and their variants are used to model various biological, biochemical, and epidemic processes [Reference Jagers1–Reference Kimmel and Axelrod4]. More recently, these methods have been used to model the spread of COVID cases in communities during the early stages of the pandemic [Reference Yanev, Stoimenova and Atanasov5, Reference Atanasov, Stoimenova and Yanev6]. As time progressed, varying local containment efforts caused changes in the number of infected members in each community [Reference Falcó and Corral7, Reference Sun, Kryven and Bianconi8], leading to periods of increase and decrease. In this paper, we describe a stochastic process model built on a branching process in random environments (BPRE) that explicitly takes into account periods of growth and decrease in the transmission rate of the virus.
Specifically, we consider a branching process model initiated by a random number of ancestors (thought of as initiators of the pandemic within a community). During the first several generations, the process grows uncontrolled, allowing immigration into the system. This initial phase is modeled using a supercritical branching process with immigration in random environments, specifically independent and identically distributed (i.i.d.) environments. When consequences of rapid spread become significant, policymakers introduce restrictions to reduce the rate of growth, hopefully resulting in a reduced number of infected cases. The limitations are modeled using upper thresholds on the number of infected cases, and beyond the threshold the process changes its character to evolve as a subcritical branching process in random environments. During this period—owing to strict controls—immigration is also not allowed. In practical terms, this period typically involves a ‘lockdown’ and other social containment efforts, the intensity of which varies across communities.
The period of restrictions is not sustainable for various reasons, including political, social, and economic pressures leading to the easing of controls. Policymakers use multiple metrics to gradually reduce controls, leading to an ‘opening of communities’, resulting in increased human interaction. As a result, or because of changes undergone by the virus, the number of infected cases increases again. We use lower thresholds in the number of ‘newly infected’ to model the period of change and let the process evolve again as a supercritical BPRE in i.i.d. environments after it crosses the lower threshold. The process continues to evolve in this manner, alternating between periods of increase and decrease. In this paper, we provide a rigorous probabilistic analysis of this model.
Although we have taken the dynamics of COVID spread as a motivation for the proposed model, the aforementioned cyclic behavior is often observed in other biological systems, such as those modeled by predator–prey models or the susceptible–infected–recovered (SIR) model. In some biological populations, the cyclical behavior can be attributed to a decline in fecundity as the population size approaches some threshold [Reference Klebaner9]. Deterministic models such as ordinary differential equations, dynamical systems, and corresponding discrete-time models are used for analysis in the applications mentioned above [Reference Teschl10–Reference Iannelli and Pugliese12]. While many of the models described above yield good qualitative descriptions, uncertainty estimates are typically unavailable. It is worth pointing out that the previously described branching process methods also produce reasonable point estimates for the mean growth during the early stages of the pandemic. However, these point estimates are unreliable during the later stages of the pandemic. In this paper, we address statistical estimation of the mean growth and characterize the variance of the estimates. We end the discussion with a plot, Figure 1, of the total number of confirmed COVID cases per week in Italy from 23 February 2020 to 20 July 2022. The plot also includes the number of cases estimated using the proposed model. Other examples with similar plots include the hare–lynx predator–prey dynamics and measles cases [Reference Iannelli and Pugliese12–Reference Hempel and Earn14].

Figure 1. In black weekly COVID cases in Italy from February 23, 2020 to February 3, 2023. In blue a BPRE starting with the same initial value and offspring mean having the negative binomial distribution with predefined number of successful trials
![]() $r=10$
and Gamma-distributed mean with shape parameter equal to the mean of the data and rate parameter 1.
$r=10$
and Gamma-distributed mean with shape parameter equal to the mean of the data and rate parameter 1.
Before we provide a precise description of our model, we begin with a brief description of BPREs with immigration. Let
![]() $\Pi_{n} = \big(P_{n},Q_{n}\big)$
be i.i.d. random variables taking values in
$\Pi_{n} = \big(P_{n},Q_{n}\big)$
be i.i.d. random variables taking values in
![]() $\mathcal{P} \times \mathcal{P}$
, where
$\mathcal{P} \times \mathcal{P}$
, where
![]() $\mathcal{P}$
is the space of probability distributions on
$\mathcal{P}$
is the space of probability distributions on
![]() $\mathbb{N}_{0}$
; that is,
$\mathbb{N}_{0}$
; that is,
![]() $P_{n}=\{ P_{n,r} \}_{r=0}^{\infty}$
and
$P_{n}=\{ P_{n,r} \}_{r=0}^{\infty}$
and
![]() $Q_{n}=\{ Q_{n,r} \}_{r=0}^{\infty}$
for some non-negative integers
$Q_{n}=\{ Q_{n,r} \}_{r=0}^{\infty}$
for some non-negative integers
![]() $P_{n,r}$
and
$P_{n,r}$
and
![]() $Q_{n,r}$
such that
$Q_{n,r}$
such that
![]() $\sum_{r=0}^{\infty} P_{n,r}=1$
and
$\sum_{r=0}^{\infty} P_{n,r}=1$
and
![]() $\sum_{r=0}^{\infty} Q_{n,r}=1$
. The process
$\sum_{r=0}^{\infty} Q_{n,r}=1$
. The process
![]() $\Pi=\{ \Pi_{n} \}_{n=0}^{\infty}$
is referred to as the environmental sequence. For each realization of
$\Pi=\{ \Pi_{n} \}_{n=0}^{\infty}$
is referred to as the environmental sequence. For each realization of
![]() $\Pi$
, we associate a population process
$\Pi$
, we associate a population process
![]() $\{ Z_{n} \}_{n=0}^{\infty}$
defined recursively as follows: let
$\{ Z_{n} \}_{n=0}^{\infty}$
defined recursively as follows: let
![]() $Z_{0}$
take values on the positive integers, and for
$Z_{0}$
take values on the positive integers, and for
![]() $n \geq 0$
, let
$n \geq 0$
, let
 \begin{equation*} Z_{n+1}=\sum_{i=1}^{Z_{n}} \xi_{n,i}+I_{n},\end{equation*}
\begin{equation*} Z_{n+1}=\sum_{i=1}^{Z_{n}} \xi_{n,i}+I_{n},\end{equation*}
where, given
![]() $\Pi_{n}=\big(P_{n},Q_{n}\big)$
,
$\Pi_{n}=\big(P_{n},Q_{n}\big)$
,
![]() $\{ \xi_{n,i} \}_{i=1}^{\infty}$
are i.i.d. with distribution
$\{ \xi_{n,i} \}_{i=1}^{\infty}$
are i.i.d. with distribution
![]() $P_{n}$
and
$P_{n}$
and
![]() $I_{n}$
is an independent random variable with distribution
$I_{n}$
is an independent random variable with distribution
![]() $Q_{n}$
. The random variable
$Q_{n}$
. The random variable
![]() $Y_{n}=\log(\overline{P}_{n})$
, where
$Y_{n}=\log(\overline{P}_{n})$
, where
![]() $\overline{P}_{n}=\sum_{r=0}^{\infty} r P_{n,r}$
, plays an important role in the classification of BPREs with immigration. It is well known that when
$\overline{P}_{n}=\sum_{r=0}^{\infty} r P_{n,r}$
, plays an important role in the classification of BPREs with immigration. It is well known that when
![]() $\mathbb{E}[Y_{0}] > 0$
, the process diverges to infinity with probability one, and if
$\mathbb{E}[Y_{0}] > 0$
, the process diverges to infinity with probability one, and if
![]() $\mathbb{E}[Y_{0}] \leq 0$
and the immigration is degenerate at zero for all environments, then the process becomes extinct with probability one [Reference Athreya and Karlin15]. Furthermore, in the subcritical case, that is,
$\mathbb{E}[Y_{0}] \leq 0$
and the immigration is degenerate at zero for all environments, then the process becomes extinct with probability one [Reference Athreya and Karlin15]. Furthermore, in the subcritical case, that is,
![]() $\mathbb{E}[Y_{0}] < 0$
, one can identify three distinct regimes: (i) weakly subcritical, (ii) moderately subcritical, and (iii) strongly subcritical. The regime (i) corresponds to the case when there exists a
$\mathbb{E}[Y_{0}] < 0$
, one can identify three distinct regimes: (i) weakly subcritical, (ii) moderately subcritical, and (iii) strongly subcritical. The regime (i) corresponds to the case when there exists a
![]() $0 < \rho < 1$
such that
$0 < \rho < 1$
such that
![]() $\mathbb{E}\big[Y_{0} e^{\rho Y_{0}}\big]=0$
, while (ii) corresponds to the case when
$\mathbb{E}\big[Y_{0} e^{\rho Y_{0}}\big]=0$
, while (ii) corresponds to the case when
![]() $\mathbb{E}[Y_{0} e^{Y_{0}}]=0$
. Finally, (iii) corresponds to the case when
$\mathbb{E}[Y_{0} e^{Y_{0}}]=0$
. Finally, (iii) corresponds to the case when
![]() $\mathbb{E}[Y_{0} e^{Y_{0}}]<0$
[Reference Kersting and Vatutin16]. In this paper, when working with the subcritical regime, we will assume that the process is strongly subcritical, and we will refer to it as a subcritical process in the rest of the manuscript.
$\mathbb{E}[Y_{0} e^{Y_{0}}]<0$
[Reference Kersting and Vatutin16]. In this paper, when working with the subcritical regime, we will assume that the process is strongly subcritical, and we will refer to it as a subcritical process in the rest of the manuscript.
We now turn to a description of the model. Let
![]() $\Pi^{U} = \{ \Pi_{n}^{U} \}_{n=0}^{\infty}$
, where
$\Pi^{U} = \{ \Pi_{n}^{U} \}_{n=0}^{\infty}$
, where
![]() $\Pi_{n}^{U}=\big(P_{n}^{U},Q_{n}^{U}\big)$
, denote a collection of supercritical environmental sequences. Here,
$\Pi_{n}^{U}=\big(P_{n}^{U},Q_{n}^{U}\big)$
, denote a collection of supercritical environmental sequences. Here,
![]() $P_{n}^{U}=\{ P_{n,r}^{U} \}_{r=0}^{\infty}$
indicates the offspring distribution and
$P_{n}^{U}=\{ P_{n,r}^{U} \}_{r=0}^{\infty}$
indicates the offspring distribution and
![]() $Q_{n}^{U}=\{ Q_{n,r}^{U} \}_{r=0}^{\infty}$
represents the immigration distribution. Also, let
$Q_{n}^{U}=\{ Q_{n,r}^{U} \}_{r=0}^{\infty}$
represents the immigration distribution. Also, let
![]() $\Pi^{L}=\{\Pi_{n}^{L}\}_{n=0}^{\infty}$
, where
$\Pi^{L}=\{\Pi_{n}^{L}\}_{n=0}^{\infty}$
, where
![]() $\Pi_{n}^{L}=P_{n}^{L}=\{ P_{n,r}^{L} \}_{r=0}^{\infty}$
, denote a collection of subcritical environmental sequences. We now provide an evolutionary description of the process: at time zero the process starts with a random number of ancestors
$\Pi_{n}^{L}=P_{n}^{L}=\{ P_{n,r}^{L} \}_{r=0}^{\infty}$
, denote a collection of subcritical environmental sequences. We now provide an evolutionary description of the process: at time zero the process starts with a random number of ancestors
![]() $Z_{0}$
. Each of them lives one unit of time and reproduces according to the distribution
$Z_{0}$
. Each of them lives one unit of time and reproduces according to the distribution
![]() $P_{0}^{U}$
. Thus, the size of the first-generation population is
$P_{0}^{U}$
. Thus, the size of the first-generation population is
 \begin{equation*} Z_{1}=\sum_{i=1}^{Z_{0}} \xi_{0,i}^{U}+I_{0}^{U},\end{equation*}
\begin{equation*} Z_{1}=\sum_{i=1}^{Z_{0}} \xi_{0,i}^{U}+I_{0}^{U},\end{equation*}
where, given
![]() $\Pi_{0}^{U}=(P_{0}^{U},Q_{0}^{U})$
, the
$\Pi_{0}^{U}=(P_{0}^{U},Q_{0}^{U})$
, the
![]() $\xi_{0,i}^{U}$
are i.i.d. random variables with offspring distribution
$\xi_{0,i}^{U}$
are i.i.d. random variables with offspring distribution
![]() $P_{0}^{U}$
and are independent of the immigration random variable
$P_{0}^{U}$
and are independent of the immigration random variable
![]() $I_{0}^{U}$
with distribution
$I_{0}^{U}$
with distribution
![]() $Q_{0}^{U}$
. The random variable
$Q_{0}^{U}$
. The random variable
![]() $\xi_{0,i}^{U}$
is interpreted as the number of children produced by the ith parent in the 0th generation, and
$\xi_{0,i}^{U}$
is interpreted as the number of children produced by the ith parent in the 0th generation, and
![]() $I_{0}^{U}$
is interpreted as the number of immigrants whose distribution is generated by the same environmental random variable
$I_{0}^{U}$
is interpreted as the number of immigrants whose distribution is generated by the same environmental random variable
![]() $\Pi^{U}_{0}$
.
$\Pi^{U}_{0}$
.
Let
![]() $U_{1}$
denote the random variable representing the upper threshold. If
$U_{1}$
denote the random variable representing the upper threshold. If
![]() $Z_{1} < U_{1}$
, each member of the first-generation population lives one unit of time and evolves, conditionally on the environment, as the ancestors independent of the population size at time one. That is,
$Z_{1} < U_{1}$
, each member of the first-generation population lives one unit of time and evolves, conditionally on the environment, as the ancestors independent of the population size at time one. That is,
 \begin{equation*} Z_{2} = \sum_{i=1}^{Z_{1}} \xi_{1,i}^{U}+I_{1}^{U}.\end{equation*}
\begin{equation*} Z_{2} = \sum_{i=1}^{Z_{1}} \xi_{1,i}^{U}+I_{1}^{U}.\end{equation*}
As before, given
![]() $\Pi_{1}^{U}=\big(P_{1}^{U},Q_{1}^{U}\big)$
, the
$\Pi_{1}^{U}=\big(P_{1}^{U},Q_{1}^{U}\big)$
, the
![]() $\xi_{1,i}^{U}$
are i.i.d. with distribution
$\xi_{1,i}^{U}$
are i.i.d. with distribution
![]() $P_{1}^{U}$
and
$P_{1}^{U}$
and
![]() $I_{1}^{U}$
has distribution
$I_{1}^{U}$
has distribution
![]() $Q_{1}^{U}$
. The random variables
$Q_{1}^{U}$
. The random variables
![]() $\xi_{1,i}^{U}$
are independent of
$\xi_{1,i}^{U}$
are independent of
![]() $Z_{1}$
,
$Z_{1}$
,
![]() $\xi_{0,i}^{U}$
, and
$\xi_{0,i}^{U}$
, and
![]() $I_{0}^{U}$
,
$I_{0}^{U}$
,
![]() $I_{1}^{U}$
. If
$I_{1}^{U}$
. If
![]() $Z_{1} \geq U_{1}$
, then
$Z_{1} \geq U_{1}$
, then
 \begin{equation*} Z_{2} = \sum_{i=1}^{Z_{1}} \xi_{1,i}^{L},\end{equation*}
\begin{equation*} Z_{2} = \sum_{i=1}^{Z_{1}} \xi_{1,i}^{L},\end{equation*}
where, given
![]() $\Pi_{1}^{L}=P_{1}^{L}$
, the
$\Pi_{1}^{L}=P_{1}^{L}$
, the
![]() $\xi_{1,i}^{L}$
are i.i.d. with distribution
$\xi_{1,i}^{L}$
are i.i.d. with distribution
![]() $P_{1}^{L}$
. Thus, the size of the second-generation population is
$P_{1}^{L}$
. Thus, the size of the second-generation population is
 \begin{equation*} Z_{2} = \begin{cases} \sum_{i=1}^{Z_{1}} \xi_{1,i}^{U}+I_{1}^{U} &\text{ if } Z_{1}<U_{1}, \\[5pt] \sum_{i=1}^{Z_{1}} \xi_{1,i}^{L} &\text{ if } Z_{1} \geq U_{1}. \end{cases}\end{equation*}
\begin{equation*} Z_{2} = \begin{cases} \sum_{i=1}^{Z_{1}} \xi_{1,i}^{U}+I_{1}^{U} &\text{ if } Z_{1}<U_{1}, \\[5pt] \sum_{i=1}^{Z_{1}} \xi_{1,i}^{L} &\text{ if } Z_{1} \geq U_{1}. \end{cases}\end{equation*}
The process
![]() $Z_{3}$
is defined recursively as before. As an example, if
$Z_{3}$
is defined recursively as before. As an example, if
![]() $Z_{1} < U_{1}$
,
$Z_{1} < U_{1}$
,
![]() $Z_{2} < U_{1}$
or
$Z_{2} < U_{1}$
or
![]() $Z_{1} \geq U_{1}$
,
$Z_{1} \geq U_{1}$
,
![]() $Z_{2} \leq L_{1}$
, for a random lower threshold
$Z_{2} \leq L_{1}$
, for a random lower threshold
![]() $L_{1}$
, then the process will evolve like a supercritical BPRE with offspring distribution
$L_{1}$
, then the process will evolve like a supercritical BPRE with offspring distribution
![]() $P_{2}^{U}$
and immigration distribution
$P_{2}^{U}$
and immigration distribution
![]() $Q_{2}^{U}$
. Otherwise (that is,
$Q_{2}^{U}$
. Otherwise (that is,
![]() $Z_1< U_1$
and
$Z_1< U_1$
and
![]() $Z_2 \ge U_1$
or
$Z_2 \ge U_1$
or
![]() $Z_1 \ge U_1$
and
$Z_1 \ge U_1$
and
![]() $Z_2 >L_1$
), the process will evolve like a subcritical BPRE with offspring distribution
$Z_2 >L_1$
), the process will evolve like a subcritical BPRE with offspring distribution
![]() $P_{2}^{L}$
. This dynamics continues with different thresholds
$P_{2}^{L}$
. This dynamics continues with different thresholds
![]() $(U_j, L_j)$
, yielding the process
$(U_j, L_j)$
, yielding the process
![]() $\{ Z_{n} \}_{n=0}^{\infty}$
, which we refer to as a branching process in random environments with thresholds (BPRET). The consecutive set of generations where the reproduction is governed by a supercritical BPRE is referred to as the supercritical regime, while the other is referred to as the subcritical regime. As we will see below, non-trivial immigration in the supercritical regime is required to obtain alternating periods of increase and decrease.
$\{ Z_{n} \}_{n=0}^{\infty}$
, which we refer to as a branching process in random environments with thresholds (BPRET). The consecutive set of generations where the reproduction is governed by a supercritical BPRE is referred to as the supercritical regime, while the other is referred to as the subcritical regime. As we will see below, non-trivial immigration in the supercritical regime is required to obtain alternating periods of increase and decrease.
The model described above is related to size-dependent branching processes with a threshold as studied by Klebaner [Reference Klebaner9] and more recently by Athreya and Schuh [Reference Athreya and Schuh17]. Specifically, in that model the offspring distribution depends on a fixed threshold K and the size of the previous generation. As observed in these papers, these Markov processes either explode to infinity or are absorbed at zero. In our model the thresholds are random and dynamic, resulting in a non-Markov process; however, the offspring distribution does not depend on the size of the previous generation as long as they belong to the same regime. Indeed, when
![]() $U_{j}-1=L_{j}=K$
for all
$U_{j}-1=L_{j}=K$
for all
![]() $j \geq 1$
, the immigration distribution is degenerate at zero, and the environment is fixed, one obtains as a special case the density-dependent branching process (see for example [Reference Klebaner9, Reference Athreya and Schuh17–Reference Jagers and Klebaner20]. Additionally, while the model of Klebaner [Reference Klebaner9] uses Galton–Watson processes as a building block, our model uses branching processes in i.i.d. environments.
$j \geq 1$
, the immigration distribution is degenerate at zero, and the environment is fixed, one obtains as a special case the density-dependent branching process (see for example [Reference Klebaner9, Reference Athreya and Schuh17–Reference Jagers and Klebaner20]. Additionally, while the model of Klebaner [Reference Klebaner9] uses Galton–Watson processes as a building block, our model uses branching processes in i.i.d. environments.
Continuing with our discussion on the literature, Athreya and Schuh [Reference Athreya and Schuh17] show that in the fixed-environment case, the special case of a size-dependent process with a single threshold becomes extinct with probability one. We show that this is also the case for the BPRE when there is no immigration; the details are in Theorem 2.1. Similar phenomena have been observed in slightly different contexts in Jagers and Zuyev [Reference Jagers and Zuyev21, Reference Jagers and Zuyev22]. The incorporation of an immigration component ensures that the process is not absorbed at zero and hence may be useful for modeling stable populations at equilibrium as done in deterministic models. For additional discussion see Section 7.
For ease of further discussion, we introduce some notation. Let
![]() $Y_{n}^{U} \;:\!=\; \log\!\Big(\overline{P}_{n}^{U}\Big)$
and
$Y_{n}^{U} \;:\!=\; \log\!\Big(\overline{P}_{n}^{U}\Big)$
and
![]() $Y_{n}^{L} \;:\!=\; \log\!\Big(\overline{P}_{n}^{L}\Big)$
, where
$Y_{n}^{L} \;:\!=\; \log\!\Big(\overline{P}_{n}^{L}\Big)$
, where
that is,
![]() $\overline{P}_{n}^{U}$
and
$\overline{P}_{n}^{U}$
and
![]() $\overline{P}_{n}^{L}$
represent the offspring means conditional on the environments
$\overline{P}_{n}^{L}$
represent the offspring means conditional on the environments
![]() $\Pi_{n}^{U}=\big(P_{n}^{U},Q_{n}^{U}\big)$
and
$\Pi_{n}^{U}=\big(P_{n}^{U},Q_{n}^{U}\big)$
and
![]() $\Pi_{n}^{L}=P_{n}^{L}$
, respectively. Also, let
$\Pi_{n}^{L}=P_{n}^{L}$
, respectively. Also, let
![]() $\overline{Q}_{n}^{U}=\sum_{r=0}^{\infty} r Q_{n,r}^{U}$
denote the immigration mean conditional on the environment, and let
$\overline{Q}_{n}^{U}=\sum_{r=0}^{\infty} r Q_{n,r}^{U}$
denote the immigration mean conditional on the environment, and let
denote the conditional variance of the offspring distributions given the environment.
From the description, it is clear that the crossing times at the thresholds
![]() $(U_{j},L_{j})$
of
$(U_{j},L_{j})$
of
![]() $Z_{n}$
, namely
$Z_{n}$
, namely
![]() $\tau_{j}$
and
$\tau_{j}$
and
![]() $\nu_{j}$
, will play a significant role in the analysis. It will turn out that
$\nu_{j}$
, will play a significant role in the analysis. It will turn out that
![]() $\{Z_{\tau_{j}}\}$
and
$\{Z_{\tau_{j}}\}$
and
![]() $\{Z_{\nu_{j}}\}$
form time-homogeneous Markov chains with state spaces
$\{Z_{\nu_{j}}\}$
form time-homogeneous Markov chains with state spaces
![]() $S^{L} \;:\!=\; \mathbb{N}_{0} \cap [0,L_{U}]$
and
$S^{L} \;:\!=\; \mathbb{N}_{0} \cap [0,L_{U}]$
and
![]() $S^{U} \;:\!=\; \mathbb{N} \cap [L_{U}+1,\infty)$
, respectively, where we take
$S^{U} \;:\!=\; \mathbb{N} \cap [L_{U}+1,\infty)$
, respectively, where we take
![]() $L_{j} \leq L_{U}$
and
$L_{j} \leq L_{U}$
and
![]() $U_{j} \geq L_{U}+1$
for all
$U_{j} \geq L_{U}+1$
for all
![]() $j \geq 1$
. Under additional conditions on the offspring distribution and the environment sequence, the processes
$j \geq 1$
. Under additional conditions on the offspring distribution and the environment sequence, the processes
![]() $\{Z_{\tau_{j}}\}$
and
$\{Z_{\tau_{j}}\}$
and
![]() $\{Z_{\nu_{j}}\}$
will be uniformly ergodic. These results are established in Section 3.
$\{Z_{\nu_{j}}\}$
will be uniformly ergodic. These results are established in Section 3.
The amount of time the process spends in the supercritical and subcritical regimes, beyond its mathematical and scientific interest, will also arise in the study of the central limit theorem for the estimates of
![]() $M^{U} \;:\!=\; \mathbb{E}\Big[\overline{P}_{n}^{U}\Big]$
and
$M^{U} \;:\!=\; \mathbb{E}\Big[\overline{P}_{n}^{U}\Big]$
and
![]() $M^{L} \;:\!=\; \mathbb{E}\Big[\overline{P}_{n}^{L}\Big]$
. Using the uniform ergodicity alluded to above, we will establish that the time averages of
$M^{L} \;:\!=\; \mathbb{E}\Big[\overline{P}_{n}^{L}\Big]$
. Using the uniform ergodicity alluded to above, we will establish that the time averages of
![]() $\tau_{j}-\nu_{j-1}$
and
$\tau_{j}-\nu_{j-1}$
and
![]() $\nu_{j}-\tau_{j}$
converge to finite positive constants,
$\nu_{j}-\tau_{j}$
converge to finite positive constants,
![]() $\mu^{U}$
and
$\mu^{U}$
and
![]() $\mu^{L}$
. Additionally, we establish a central limit theorem related to this convergence under a finite-second-moment hypothesis after an appropriate centering and scaling, that is,
$\mu^{L}$
. Additionally, we establish a central limit theorem related to this convergence under a finite-second-moment hypothesis after an appropriate centering and scaling, that is,
 \begin{align*} \frac{1}{\sqrt{n}}\sum_{j=1}^n (\tau_j -\nu_{j-1}) \xrightarrow[n \to \infty]{d} N\big( \mu^U, \sigma^{2,U}\big),\end{align*}
\begin{align*} \frac{1}{\sqrt{n}}\sum_{j=1}^n (\tau_j -\nu_{j-1}) \xrightarrow[n \to \infty]{d} N\big( \mu^U, \sigma^{2,U}\big),\end{align*}
and we characterize
![]() $\sigma^{2,U}$
in terms of the stationary distribution of the Markov chain. A similar result also holds for
$\sigma^{2,U}$
in terms of the stationary distribution of the Markov chain. A similar result also holds for
![]() $\nu_j-\tau_{j}$
. This, in turn, provides qualitative information regarding the proportion of time the process spends in these regimes. That is, if
$\nu_j-\tau_{j}$
. This, in turn, provides qualitative information regarding the proportion of time the process spends in these regimes. That is, if
![]() $C_{n}^{U}$
is the amount of time the process spends in the supercritical regime up to time
$C_{n}^{U}$
is the amount of time the process spends in the supercritical regime up to time
![]() $n-1$
, we show that
$n-1$
, we show that
![]() $n^{-1}C_n^{U}$
converges to
$n^{-1}C_n^{U}$
converges to
![]() $\mu^U\big(\mu^U+\mu^L\big)^{-1}$
; a related central limit theorem is also established, and in the process we characterize the limiting variance. Interestingly, we show that the central limit theorem prevails even for the joint distribution of the length of time and the proportion of time the process spends in the supercritical and subcritical regimes. These results are described in Sections 4 and 5.
$\mu^U\big(\mu^U+\mu^L\big)^{-1}$
; a related central limit theorem is also established, and in the process we characterize the limiting variance. Interestingly, we show that the central limit theorem prevails even for the joint distribution of the length of time and the proportion of time the process spends in the supercritical and subcritical regimes. These results are described in Sections 4 and 5.
An interesting question concerns the rate of growth of the BPRET in the supercritical and subcritical regimes described by the corresponding expectations, namely
![]() $M^{U}$
and
$M^{U}$
and
![]() $M^{L}$
. Specifically, we establish that the limiting joint distribution of the estimators is bivariate normal with a diagonal covariance matrix, yielding asymptotic independence of the mean estimators derived using data from supercritical and subcritical regimes. In the classical setting of a supercritical BPRE without immigration, this problem has received some attention (see for instance Dion and Esty [Reference Yanev, Stoimenova and Atanasov23]). The problem considered here is different in the following four ways: (i) the population size does not converge to infinity, (ii) the lengths of the regimes are random, (iii) in the supercritical regime the population size may be zero, and (iv) there is an additional immigration term. While (iii) and (iv) can be accounted for in the classical settings as well, their effect on the point estimates is minimized because of the exponential growth of the population size. Here, while the exponential growth is ruled out, perhaps as anticipated, the Markov property of the process at crossing times, namely
$M^{L}$
. Specifically, we establish that the limiting joint distribution of the estimators is bivariate normal with a diagonal covariance matrix, yielding asymptotic independence of the mean estimators derived using data from supercritical and subcritical regimes. In the classical setting of a supercritical BPRE without immigration, this problem has received some attention (see for instance Dion and Esty [Reference Yanev, Stoimenova and Atanasov23]). The problem considered here is different in the following four ways: (i) the population size does not converge to infinity, (ii) the lengths of the regimes are random, (iii) in the supercritical regime the population size may be zero, and (iv) there is an additional immigration term. While (iii) and (iv) can be accounted for in the classical settings as well, their effect on the point estimates is minimized because of the exponential growth of the population size. Here, while the exponential growth is ruled out, perhaps as anticipated, the Markov property of the process at crossing times, namely
![]() $\{Z_{\tau_j}\}$
and
$\{Z_{\tau_j}\}$
and
![]() $\{Z_{\nu_j}\}$
, and their associated regeneration times plays a central role in the proof. It is important to note that it is possible for both regimes to occur between regeneration times. Hence, the proportion of time that the process spends in the supercritical and subcritical regimes also plays a vital role in the derivation of the asymptotic limit distribution. The limiting variance of the estimators depends additionally on
$\{Z_{\nu_j}\}$
, and their associated regeneration times plays a central role in the proof. It is important to note that it is possible for both regimes to occur between regeneration times. Hence, the proportion of time that the process spends in the supercritical and subcritical regimes also plays a vital role in the derivation of the asymptotic limit distribution. The limiting variance of the estimators depends additionally on
![]() $\mu^{U}$
and
$\mu^{U}$
and
![]() $\mu^{L}$
, beyond
$\mu^{L}$
, beyond
![]() $V_{1}^{U} \;:\!=\; \mathbb{V}\Big[\overline{P}_{0}^{U}\Big]$
,
$V_{1}^{U} \;:\!=\; \mathbb{V}\Big[\overline{P}_{0}^{U}\Big]$
,
![]() $V_{1}^{L} \;:\!=\; \mathbb{V}\Big[\overline{P}_{0}^{L}\Big]$
,
$V_{1}^{L} \;:\!=\; \mathbb{V}\Big[\overline{P}_{0}^{L}\Big]$
,
![]() $V_{2}^{U} \;:\!=\; \mathbb{E}\Big[\overline{\overline{P}}_{0}^{U}\Big]$
, and
$V_{2}^{U} \;:\!=\; \mathbb{E}\Big[\overline{\overline{P}}_{0}^{U}\Big]$
, and
![]() $V_{2}^{L} \;:\!=\; \mathbb{E}\Big[\overline{\overline{P}}_{0}^{L}\Big]$
. In the special case of fixed environments, the limit behavior of the estimators takes a different form compared to the traditional results, as described for example in Heyde [Reference Heyde24]. These results are in Section 6.
$V_{2}^{L} \;:\!=\; \mathbb{E}\Big[\overline{\overline{P}}_{0}^{L}\Big]$
. In the special case of fixed environments, the limit behavior of the estimators takes a different form compared to the traditional results, as described for example in Heyde [Reference Heyde24]. These results are in Section 6.
Finally, in Appendix B we provide some numerical experiments illustrating the behavior of the model. Specifically, we illustrate the effects of different distributions on the path behavior of the process and describe how they change when the thresholds increase. The experiments also suggests that if different regimes are not taken into account, the true growth rate of the virus may be underestimated. We now turn to Section 2, where we develop additional notation and provide precise statements of the main results.
2. Main results
The branching process in random environments with thresholds (BPRET) is a supercritical BPRE with immigration until it reaches an upper threshold, after which it transitions to a subcritical BPRE until it crosses a lower threshold. Beyond this time, the process reverts to a supercritical BPRE with immigration, and the above cycle continues. Specifically, let
![]() $\{ (U_{j},L_{j}) \}_{j=1}^{\infty}$
denote a collection of thresholds (assumed to be i.i.d.). Then the BPRET evolves like a supercritical BPRE with immigration until it reaches the upper threshold
$\{ (U_{j},L_{j}) \}_{j=1}^{\infty}$
denote a collection of thresholds (assumed to be i.i.d.). Then the BPRET evolves like a supercritical BPRE with immigration until it reaches the upper threshold
![]() $U_{1}$
, at which time it becomes a subcritical BPRE. The process remains subcritical until it crosses the threshold
$U_{1}$
, at which time it becomes a subcritical BPRE. The process remains subcritical until it crosses the threshold
![]() $L_{1}$
; after that it evolves again as a supercritical BPRE with immigration, and so on. We now provide a precise description of the BPRET.
$L_{1}$
; after that it evolves again as a supercritical BPRE with immigration, and so on. We now provide a precise description of the BPRET.
Let
![]() $\{ (U_{j},L_{j})\}_{j=1}^{\infty}$
be i.i.d. random vectors with support
$\{ (U_{j},L_{j})\}_{j=1}^{\infty}$
be i.i.d. random vectors with support
![]() $S_{B}^{U} \times S_{B}^{L}$
, where
$S_{B}^{U} \times S_{B}^{L}$
, where
![]() $S_{B}^{U} \;:\!=\; \mathbb{N} \cap [L_U+1, \infty)$
,
$S_{B}^{U} \;:\!=\; \mathbb{N} \cap [L_U+1, \infty)$
,
![]() $S_{B}^{L} \;:\!=\; \mathbb{N} \cap [L_{0}, L_{U}]$
, and
$S_{B}^{L} \;:\!=\; \mathbb{N} \cap [L_{0}, L_{U}]$
, and
![]() $1 \leq L_{0} \leq L_{U}$
are fixed integers. We denote by
$1 \leq L_{0} \leq L_{U}$
are fixed integers. We denote by
![]() $\Pi^{U}$
and
$\Pi^{U}$
and
![]() $\Pi^{L}$
the supercritical and subcritical environmental sequences; that is,
$\Pi^{L}$
the supercritical and subcritical environmental sequences; that is,
We use the notation
![]() $\mathbb{P}_{E^{U}}$
and
$\mathbb{P}_{E^{U}}$
and
![]() $\mathbb{P}_{E^{L}}$
for probability statements with respect to the supercritical and subcritical environmental sequences. As in the introduction, given the environment, the
$\mathbb{P}_{E^{L}}$
for probability statements with respect to the supercritical and subcritical environmental sequences. As in the introduction, given the environment, the
![]() $\xi_{n,i}^{U}$
are i.i.d. random variables with distribution
$\xi_{n,i}^{U}$
are i.i.d. random variables with distribution
![]() $P_{n}^{U}$
and are independent of the immigration random variable
$P_{n}^{U}$
and are independent of the immigration random variable
![]() $I_{n}^{U}$
. Similarly, conditionally on the environment, the
$I_{n}^{U}$
. Similarly, conditionally on the environment, the
![]() $\xi_{n,i}^{L}$
are i.i.d. random variables with offspring distribution
$\xi_{n,i}^{L}$
are i.i.d. random variables with offspring distribution
![]() $P_{n}^{L}$
. Finally, let
$P_{n}^{L}$
. Finally, let
![]() $Z_{0}$
be an independent random variable with support included in
$Z_{0}$
be an independent random variable with support included in
![]() $\mathbb{N} \cap [1, L_{U}]$
. We emphasize that the thresholds are independent of the environmental sequences, offspring random variables, immigration random variables, and
$\mathbb{N} \cap [1, L_{U}]$
. We emphasize that the thresholds are independent of the environmental sequences, offspring random variables, immigration random variables, and
![]() $Z_{0}$
. For technical details regarding the construction of the probability space we refer the reader to Appendix A.1. We denote by
$Z_{0}$
. For technical details regarding the construction of the probability space we refer the reader to Appendix A.1. We denote by
![]() $M^{T} \;:\!=\; \mathbb{E}\Big[\overline{P}_{0}^{T}\Big]$
,
$M^{T} \;:\!=\; \mathbb{E}\Big[\overline{P}_{0}^{T}\Big]$
,
![]() $T \in \{ L, U \}$
, and
$T \in \{ L, U \}$
, and
![]() $N^{U} \;:\!=\; \mathbb{E}\Big[\overline{Q}_{0}^{U}\Big]$
the annealed (averaged over the environment) offspring mean and the annealed immigration mean, respectively. Throughout the manuscript, we make the following assumptions on the environmental sequences.
$N^{U} \;:\!=\; \mathbb{E}\Big[\overline{Q}_{0}^{U}\Big]$
the annealed (averaged over the environment) offspring mean and the annealed immigration mean, respectively. Throughout the manuscript, we make the following assumptions on the environmental sequences.
Assumptions:
-
(H1)
 $\Pi^{T} = \big\{ \Pi_{n}^{T} \big\}_{n=0}^{\infty}$
are i.i.d. environments such that
$\Pi^{T} = \big\{ \Pi_{n}^{T} \big\}_{n=0}^{\infty}$
are i.i.d. environments such that
 $P_{0,0}^{T}<1$
and
$P_{0,0}^{T}<1$
and
 $0 < \overline{P}_{0}^{T} < \infty$
$0 < \overline{P}_{0}^{T} < \infty$
 $\mathbb{P}_{E^{T}}$
-almost surely (a.s.).
$\mathbb{P}_{E^{T}}$
-almost surely (a.s.). -
(H2)
 $\mathbb{E}\Big[Y_{0}^{L} e^{Y_{0}^{L}}\Big] < 0$
,
$\mathbb{E}\Big[Y_{0}^{L} e^{Y_{0}^{L}}\Big] < 0$
,
 $\mathbb{E}\big[Y_{0}^{U}\big] >0$
,
$\mathbb{E}\big[Y_{0}^{U}\big] >0$
,
 $M^{U} < \infty$
, and
$M^{U} < \infty$
, and
 $\mathbb{E}\big[\!\log\!\big(1-P_{0,0}^{U}\big)\big]>-\infty$
.
$\mathbb{E}\big[\!\log\!\big(1-P_{0,0}^{U}\big)\big]>-\infty$
. -
(H3)
 $\mathbb{P}_{E^{U}}(Q_{0,0}^{U}<1)>0$
and
$\mathbb{P}_{E^{U}}(Q_{0,0}^{U}<1)>0$
and
 $N^{U}<\infty$
.
$N^{U}<\infty$
. -
(H4)
 $\big\{(U_{j}, L_{j})\big\}_{j=1}^{\infty}$
are i.i.d. and have support
$\big\{(U_{j}, L_{j})\big\}_{j=1}^{\infty}$
are i.i.d. and have support
 $S_{B}^{U} \times S_{B}^{L}$
, where
$S_{B}^{U} \times S_{B}^{L}$
, where
 $1 \leq L_{0} \leq M^{L} L_{U}$
and
$1 \leq L_{0} \leq M^{L} L_{U}$
and
 $\mathbb{E}[U_{1}]<\infty$
.
$\mathbb{E}[U_{1}]<\infty$
.
The above assumptions rule out degenerate behavior of the process and are commonly used in the literature on BPRE (see Assumption R and Theorem 2.2 of Kersting and Vatutin [Reference Kersting and Vatutin16]). Assumption (
H2
) states that
![]() $\Pi_{n}^{U}$
is a supercritical environment and
$\Pi_{n}^{U}$
is a supercritical environment and
![]() $\Pi_{n}^{L}$
is a (strongly) subcritical environment. Additionally, by Jensen’s inequality it follows that
$\Pi_{n}^{L}$
is a (strongly) subcritical environment. Additionally, by Jensen’s inequality it follows that
![]() $M^{L} < 1$
and
$M^{L} < 1$
and
![]() $1 < M^{U} < \infty$
. Assumption (
H3
) states that immigration is positive with positive probability and has finite expectation
$1 < M^{U} < \infty$
. Assumption (
H3
) states that immigration is positive with positive probability and has finite expectation
![]() $N^{U}$
, while (
H4
) states that the upper thresholds
$N^{U}$
, while (
H4
) states that the upper thresholds
![]() $U_{j}$
have finite expectation.
$U_{j}$
have finite expectation.
We are now ready to give a precise definition of the BPRET. Let
![]() $\nu_{0} \;:\!=\; 0$
. Starting from
$\nu_{0} \;:\!=\; 0$
. Starting from
![]() $Z_{0}$
, the BPRET
$Z_{0}$
, the BPRET
![]() $\{ Z_{n} \}_{n=0}^{\infty}$
is defined recursively over
$\{ Z_{n} \}_{n=0}^{\infty}$
is defined recursively over
![]() $j \geq 0$
as follows:
$j \geq 0$
as follows:
-
1j. For
 $n \geq \nu_{j}$
and until
$n \geq \nu_{j}$
and until
 $Z_{n} < U_{j+1}$
, (1)Next, let
$Z_{n} < U_{j+1}$
, (1)Next, let \begin{equation} Z_{n+1} = \sum_{i=1}^{Z_n} \xi_{n,i}^{U} + I_{n}^{U}.\end{equation}
\begin{equation} Z_{n+1} = \sum_{i=1}^{Z_n} \xi_{n,i}^{U} + I_{n}^{U}.\end{equation}
 $\tau_{j+1} \;:\!=\; \inf\{n \ge \nu_{j} \;:\; Z_{n} \ge U_{j+1}\}$
.
$\tau_{j+1} \;:\!=\; \inf\{n \ge \nu_{j} \;:\; Z_{n} \ge U_{j+1}\}$
.
-
2j. For
 $n \geq \tau_{j+1}$
and until
$n \geq \tau_{j+1}$
and until
 $Z_{n} > L_{j+1}$
, (2)Next, let
$Z_{n} > L_{j+1}$
, (2)Next, let \begin{equation} Z_{n+1} = \sum_{i=1}^{Z_n} \xi_{n,i}^{L}.\end{equation}
\begin{equation} Z_{n+1} = \sum_{i=1}^{Z_n} \xi_{n,i}^{L}.\end{equation}
 $\nu_{j+1} \;:\!=\; \inf \{ n \geq \tau_{j+1} \;:\; Z_{n} \leq L_{j+1} \}$
.
$\nu_{j+1} \;:\!=\; \inf \{ n \geq \tau_{j+1} \;:\; Z_{n} \leq L_{j+1} \}$
.
It is clear from the definition that
![]() $\nu_{j}$
and
$\nu_{j}$
and
![]() $\tau_{j}$
are stopping times with respect to the
$\tau_{j}$
are stopping times with respect to the
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\mathcal{F}_{n}$
generated by
$\mathcal{F}_{n}$
generated by
![]() $\{ Z_{j} \}_{j=0}^{n}$
and the thresholds
$\{ Z_{j} \}_{j=0}^{n}$
and the thresholds
![]() $\{ (U_{j},L_{j}) \}_{j=1}^{\infty}$
. Thus,
$\{ (U_{j},L_{j}) \}_{j=1}^{\infty}$
. Thus,
![]() $Z_{\nu_{j}}$
,
$Z_{\nu_{j}}$
,
![]() $Z_{\tau_{j}}$
,
$Z_{\tau_{j}}$
,
![]() $\xi_{\nu_{j},i}^{U}$
,
$\xi_{\nu_{j},i}^{U}$
,
![]() $\xi_{\tau_{j+1},i}^{L}$
, and
$\xi_{\tau_{j+1},i}^{L}$
, and
![]() $I_{\nu_{j}}^{U}$
are well-defined random variables.
$I_{\nu_{j}}^{U}$
are well-defined random variables.
It is also clear from the above definition that the intervals
![]() $[\nu_{j-1},\tau_{j})$
and
$[\nu_{j-1},\tau_{j})$
and
![]() $[\tau_{j},\nu_{j})$
represent supercritical and subcritical intervals, respectively. We show below that the process
$[\tau_{j},\nu_{j})$
represent supercritical and subcritical intervals, respectively. We show below that the process
![]() $\{ Z_{n} \}_{n=0}^{\infty}$
exits and enters the above intervals infinitely often. Let
$\{ Z_{n} \}_{n=0}^{\infty}$
exits and enters the above intervals infinitely often. Let
![]() $\Delta_{j}^{U} \;:\!=\; \tau_{j}-\nu_{j-1}$
and
$\Delta_{j}^{U} \;:\!=\; \tau_{j}-\nu_{j-1}$
and
![]() $\Delta_{j}^{L} \;:\!=\; \nu_{j}-\tau_{j}$
denote the lengths of these intervals. Since a supercritical BPRE with immigration diverges with probability one (see Theorem 2.2 of Kersting and Vatutin [Reference Kersting and Vatutin16]), it follows that
$\Delta_{j}^{L} \;:\!=\; \nu_{j}-\tau_{j}$
denote the lengths of these intervals. Since a supercritical BPRE with immigration diverges with probability one (see Theorem 2.2 of Kersting and Vatutin [Reference Kersting and Vatutin16]), it follows that
![]() $\tau_{j+1}$
is finite whenever
$\tau_{j+1}$
is finite whenever
![]() $\nu_{j}$
is finite:
$\nu_{j}$
is finite:
We emphasize that Assumption (
H3
) is required, since otherwise, if
![]() $I_{0}^{U} \equiv 0$
, the process may fail to cross the upper threshold and thus may become extinct (see Theorem 2.1 below). On the other hand, since a strongly subcritical BPRE becomes extinct with probability one,
$I_{0}^{U} \equiv 0$
, the process may fail to cross the upper threshold and thus may become extinct (see Theorem 2.1 below). On the other hand, since a strongly subcritical BPRE becomes extinct with probability one,
![]() $\Delta_{j+1}^{L}<\infty$
whenever
$\Delta_{j+1}^{L}<\infty$
whenever
![]() $\tau_{j+1}<\infty$
; that is,
$\tau_{j+1}<\infty$
; that is,
Using
![]() $\nu_{0}=0$
and induction over j, we see that
$\nu_{0}=0$
and induction over j, we see that
![]() $\Delta_{j+1}^{U}$
,
$\Delta_{j+1}^{U}$
,
![]() $\Delta_{j+1}^{L}$
,
$\Delta_{j+1}^{L}$
,
![]() $\tau_{j+1}$
, and
$\tau_{j+1}$
, and
![]() $\nu_{j+1}$
are finite a.s. We emphasize that (4) holds whenever
$\nu_{j+1}$
are finite a.s. We emphasize that (4) holds whenever
![]() $\Pi^{L}$
is a subcritical or critical (but not strongly critical) environmental sequence (see Definition 2.3 in Kersting and Vatutin [Reference Kersting and Vatutin16]). That is, it remains valid if the assumption
$\Pi^{L}$
is a subcritical or critical (but not strongly critical) environmental sequence (see Definition 2.3 in Kersting and Vatutin [Reference Kersting and Vatutin16]). That is, it remains valid if the assumption
![]() $\mathbb{E}\Big[Y_{0}^{L} e^{Y_{0}^{L}}\Big] < 0$
in (
H2
) is weakened to
$\mathbb{E}\Big[Y_{0}^{L} e^{Y_{0}^{L}}\Big] < 0$
in (
H2
) is weakened to
![]() $\mathbb{E}\big[Y_{0}^{L}\big] \leq 0$
and
$\mathbb{E}\big[Y_{0}^{L}\big] \leq 0$
and
![]() $\mathbb{P}_{E^{L}}\big(Y_{0}^{L} \neq 0\big)>0$
, which leads to the following assumption:
$\mathbb{P}_{E^{L}}\big(Y_{0}^{L} \neq 0\big)>0$
, which leads to the following assumption:
-
(H2′ )
 $\mathbb{E}\big[Y_{0}^{L}\big] \leq 0$
,
$\mathbb{E}\big[Y_{0}^{L}\big] \leq 0$
,
 $\mathbb{P}_{E^{L}}\big(Y_{0}^{L} \neq 0\big)>0$
, and
$\mathbb{P}_{E^{L}}\big(Y_{0}^{L} \neq 0\big)>0$
, and
 $\mathbb{E}\big[Y_{0}^{U}\big] >0$
.
$\mathbb{E}\big[Y_{0}^{U}\big] >0$
.
The next theorem shows that if immigration is zero, the process becomes extinct a.s.
Theorem 2.1.
Assume (
H1
), (
H2′
), and
![]() $Q_{0,0}^{U} \equiv 1$
a.s. Let
$Q_{0,0}^{U} \equiv 1$
a.s. Let
![]() $\mathrm{T} \;:\!=\; \inf\{n \ge 1 \;:\; Z_n=0 \}$
. Then
$\mathrm{T} \;:\!=\; \inf\{n \ge 1 \;:\; Z_n=0 \}$
. Then
![]() $\mathbb{P}(\mathrm{T}<\infty)=1$
.
$\mathbb{P}(\mathrm{T}<\infty)=1$
.
Theorem 1 of Athreya and Schuh [Reference Kersting and Vatutin16] follows from the above theorem by taking
![]() $L_{U}=K$
,
$L_{U}=K$
,
![]() $L_{j} \equiv K$
,
$L_{j} \equiv K$
,
![]() $U_{j} \equiv K+1$
, where K is a finite positive integer, and assuming that the environments are fixed in both regimes.
$U_{j} \equiv K+1$
, where K is a finite positive integer, and assuming that the environments are fixed in both regimes.
2.1. Path properties of BPRET
We now turn to transience and recurrence of the BPRET
![]() $\{Z_{n}\}_{n=0}^{\infty}$
. Notice that even though
$\{Z_{n}\}_{n=0}^{\infty}$
. Notice that even though
![]() $\{Z_{n}\}_{n=0}^{\infty}$
is not Markov, the concepts of recurrence and transience can be studied using the definition given below (due to [Reference Lamperti25, Reference Lamperti26]).
$\{Z_{n}\}_{n=0}^{\infty}$
is not Markov, the concepts of recurrence and transience can be studied using the definition given below (due to [Reference Lamperti25, Reference Lamperti26]).
Definition 2.1. A non-negative stochastic process
![]() $\{X_n\}_{n=0}^{\infty}$
satisfying
$\{X_n\}_{n=0}^{\infty}$
satisfying
![]() $\mathbb{P}(\!\limsup_{n \rightarrow \infty} X_n= \infty)=1$
is said to be recurrent if there exists an
$\mathbb{P}(\!\limsup_{n \rightarrow \infty} X_n= \infty)=1$
is said to be recurrent if there exists an
![]() $ r < \infty$
such that
$ r < \infty$
such that
![]() $\mathbb{P}(\!\liminf_{n \rightarrow \infty} X_n \le r)=1$
, and transient if
$\mathbb{P}(\!\liminf_{n \rightarrow \infty} X_n \le r)=1$
, and transient if
![]() $\mathbb{P}(\!\lim_{n \rightarrow \infty} X_n=\infty)=1$
.
$\mathbb{P}(\!\lim_{n \rightarrow \infty} X_n=\infty)=1$
.
Our next result is concerned with the path behavior of
![]() $\{ Z_{n} \}_{n =0 }^{\infty}$
and the stopped sequences
$\{ Z_{n} \}_{n =0 }^{\infty}$
and the stopped sequences
![]() $\big\{ Z_{\nu_{j}} \big\}_{j = 0 }^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j = 0 }^{\infty}$
and
![]() $\big\{ Z_{\tau_{j}} \big\}_{j = 1 }^{\infty}$
.
$\big\{ Z_{\tau_{j}} \big\}_{j = 1 }^{\infty}$
.
Theorem 2.2. Assume ( H1 )–( H4 ). Then
-
(i) the process
 $\{ Z_{n} \}_{n=0}^{\infty}$
is recurrent;
$\{ Z_{n} \}_{n=0}^{\infty}$
is recurrent; -
(ii)
 $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
 $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
are time-homogeneous Markov chains.
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
are time-homogeneous Markov chains.
We now turn to the ergodicity properties of
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
. These rely on conditions on the offspring distribution that ensure that the Markov chains
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
. These rely on conditions on the offspring distribution that ensure that the Markov chains
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
are irreducible and aperiodic. While several sufficient conditions are possible, we provide below some possible conditions:
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
are irreducible and aperiodic. While several sufficient conditions are possible, we provide below some possible conditions:
-
(H5)
 $\mathbb{P}_{E^{L}}\big(\!\cap_{r=0}^{1} \big\{ P_{0,r}^{L} > 0 \big\} \big)>0$
.
$\mathbb{P}_{E^{L}}\big(\!\cap_{r=0}^{1} \big\{ P_{0,r}^{L} > 0 \big\} \big)>0$
. -
(H6)
 $\mathbb{P}_{E^{U}}\big(\!\cap_{r=0}^{\infty} \big\{ P_{0,r}^{U}>0 \big\} \cap \big\{ Q_{0,0}^{U}>0 \big\}\big)>0$
and
$\mathbb{P}_{E^{U}}\big(\!\cap_{r=0}^{\infty} \big\{ P_{0,r}^{U}>0 \big\} \cap \big\{ Q_{0,0}^{U}>0 \big\}\big)>0$
and
 $\mathbb{P}_{E^{U}}\big(Q_{0,s}^{U}>0\big)>0$
for some
$\mathbb{P}_{E^{U}}\big(Q_{0,s}^{U}>0\big)>0$
for some
 $s \in \{ 1, \dots, L_{U} \}$
.
$s \in \{ 1, \dots, L_{U} \}$
. -
(H7)
 $\mathbb{P}_{E^{U}}\big( \big\{P_{0,0}^{U}>0\big\} \cap \cap_{r=L_{U}+1}^{\infty} \big\{ Q_{0,r}^{U}>0\big\}\big)> 0$
.
$\mathbb{P}_{E^{U}}\big( \big\{P_{0,0}^{U}>0\big\} \cap \cap_{r=L_{U}+1}^{\infty} \big\{ Q_{0,r}^{U}>0\big\}\big)> 0$
.
The condition (
H5
) requires that on a set of positive
![]() $\mathbb{P}_{E^{L}}$
probability, an individual can produce zero and one offspring, while (
H6
) requires that on a set of positive
$\mathbb{P}_{E^{L}}$
probability, an individual can produce zero and one offspring, while (
H6
) requires that on a set of positive
![]() $\mathbb{P}_{E^{U}}$
probability,
$\mathbb{P}_{E^{U}}$
probability,
![]() $P_{0,r}^{U}>0$
for all
$P_{0,r}^{U}>0$
for all
![]() $r \in \mathbb{N}_{0}$
and
$r \in \mathbb{N}_{0}$
and
![]() $Q_{0,0}^{U}> 0$
. Also, on a set of positive
$Q_{0,0}^{U}> 0$
. Also, on a set of positive
![]() $\mathbb{P}_{E^{U}}$
probability,
$\mathbb{P}_{E^{U}}$
probability,
![]() $Q_{0,s}^{U}>0$
for some
$Q_{0,s}^{U}>0$
for some
![]() $s \in \{ 1, \dots, L_{U} \}$
. Finally, (
H7
) states that on a set of positive
$s \in \{ 1, \dots, L_{U} \}$
. Finally, (
H7
) states that on a set of positive
![]() $\mathbb{P}_{E^{U}}$
probability,
$\mathbb{P}_{E^{U}}$
probability,
![]() $P_{0,0}^{U}>0$
and
$P_{0,0}^{U}>0$
and
![]() $Q_{0,r}^{U}>0$
for all
$Q_{0,r}^{U}>0$
for all
![]() $r \geq L_{U}+1$
. These are weak conditions on the environment sequences and are part of the standard BPRE literature. We recall that
$r \geq L_{U}+1$
. These are weak conditions on the environment sequences and are part of the standard BPRE literature. We recall that
![]() $S^{L}$
is the set of non-negative integers not larger than
$S^{L}$
is the set of non-negative integers not larger than
![]() $L_{U}$
, and
$L_{U}$
, and
![]() $S^{U}$
is the set of integers larger than
$S^{U}$
is the set of integers larger than
![]() $L_{U}$
.
$L_{U}$
.
Theorem 2.3.
Assume (
H1
)–(
H4
). (i) If (
H5
) also holds, then
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
is a uniformly ergodic Markov chain with state space
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
is a uniformly ergodic Markov chain with state space
![]() $S^{L}$
. (ii) If (
H6
) (or (
H7
)) holds, then
$S^{L}$
. (ii) If (
H6
) (or (
H7
)) holds, then
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
is a uniformly ergodic Markov chain with state space
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
is a uniformly ergodic Markov chain with state space
![]() $S^{U}$
.
$S^{U}$
.
When the assumptions (
H1
)–(
H6
) (or (
H7
)) hold, we denote by
![]() $\pi^{L} = \{ \pi^{L}_{i} \}_{i \in S^{L}}$
and
$\pi^{L} = \{ \pi^{L}_{i} \}_{i \in S^{L}}$
and
![]() $\pi^{U} = \{ \pi^{U}_{i} \}_{i \in S^{U}}$
the stationary distributions of the ergodic Markov chains
$\pi^{U} = \{ \pi^{U}_{i} \}_{i \in S^{U}}$
the stationary distributions of the ergodic Markov chains
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
, respectively. While
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
, respectively. While
![]() $\pi^{L}$
has moments of all orders, we show in Proposition A.1 below that
$\pi^{L}$
has moments of all orders, we show in Proposition A.1 below that
![]() $\pi^{U}$
has a finite first moment. These distributions will play a significant role in the study of the lengths of the supercritical and subcritical regimes, which we now undertake.
$\pi^{U}$
has a finite first moment. These distributions will play a significant role in the study of the lengths of the supercritical and subcritical regimes, which we now undertake.
2.2. Lengths of supercritical and subcritical regimes
We now turn to the law of large numbers and central limit theorem for the differences
![]() $\Delta_{j}^{U}$
and
$\Delta_{j}^{U}$
and
![]() $\Delta_{j}^{L}$
. We denote by
$\Delta_{j}^{L}$
. We denote by
![]() $\mathbb{P}_{\pi^{L}}(\!\cdot\!)$
,
$\mathbb{P}_{\pi^{L}}(\!\cdot\!)$
,
![]() $\mathbb{E}_{\pi^{L}}[\!\cdot\!]$
,
$\mathbb{E}_{\pi^{L}}[\!\cdot\!]$
,
![]() $\mathbb{V}_{\pi^{L}}[\!\cdot\!]$
, and
$\mathbb{V}_{\pi^{L}}[\!\cdot\!]$
, and
![]() $\mathbb{C}_{\pi^{L}}[\cdot,\cdot]$
the probability, expectation, variance, and covariance conditionally on
$\mathbb{C}_{\pi^{L}}[\cdot,\cdot]$
the probability, expectation, variance, and covariance conditionally on
![]() $Z_{\nu_{0}} \sim \pi^{L}$
. Similarly, when
$Z_{\nu_{0}} \sim \pi^{L}$
. Similarly, when
![]() $\pi^{L}$
is replaced by
$\pi^{L}$
is replaced by
![]() $\pi^{U}$
in the above quantities, we understand that they are conditioned on
$\pi^{U}$
in the above quantities, we understand that they are conditioned on
![]() $Z_{\tau_{1}} \sim \pi^{U}$
. We define
$Z_{\tau_{1}} \sim \pi^{U}$
. We define
![]() $\mu^{U} \;:\!=\; \mathbb{E}_{\pi^{L}}\big[\Delta_{1}^{U}\big]$
,
$\mu^{U} \;:\!=\; \mathbb{E}_{\pi^{L}}\big[\Delta_{1}^{U}\big]$
,
![]() $\mu^{L} \;:\!=\; \mathbb{E}_{\pi^{U}}\big[\Delta_{1}^{L}\big]$
,
$\mu^{L} \;:\!=\; \mathbb{E}_{\pi^{U}}\big[\Delta_{1}^{L}\big]$
,
 \begin{align} \sigma^{2,U} \;:\!=\; & \mathbb{V}_{\pi^{L}}\big[\Delta_{1}^{U}\big] + 2 \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{L}}\big[\Delta_{1}^{U}, \Delta_{j+1}^{U}\big], \quad \text{ and } \end{align}
\begin{align} \sigma^{2,U} \;:\!=\; & \mathbb{V}_{\pi^{L}}\big[\Delta_{1}^{U}\big] + 2 \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{L}}\big[\Delta_{1}^{U}, \Delta_{j+1}^{U}\big], \quad \text{ and } \end{align}
 \begin{align} \sigma^{2,L} \;:\!=\; & \mathbb{V}_{\pi^{U}}\big[\Delta_{1}^{L}\big] + 2 \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{U}}\big[\Delta_{1}^{L}, \Delta_{j+1}^{L} \big]. \end{align}
\begin{align} \sigma^{2,L} \;:\!=\; & \mathbb{V}_{\pi^{U}}\big[\Delta_{1}^{L}\big] + 2 \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{U}}\big[\Delta_{1}^{L}, \Delta_{j+1}^{L} \big]. \end{align}
In the supercritical regime, we impose the additional assumption ( H8 ) below, to avoid needing to qualify our statements with the phrase ‘on the set of non-extinction’. Assumption ( H9 ) below ensures that the immigration distribution stochastically dominates the upper threshold.
-
(H8)
 $P_{0,0}^{U} = 0$
$P_{0,0}^{U} = 0$
 $\mathbb{P}_{E^{U}}$
-a.s.
$\mathbb{P}_{E^{U}}$
-a.s. -
(H9)
 $\mathbb{E}\Big[\frac{U_{1}}{\mathbb{P}(I_{0}^{U^{\,}} \geq U_{1} | U_{1})}\Big]<\infty$
.
$\mathbb{E}\Big[\frac{U_{1}}{\mathbb{P}(I_{0}^{U^{\,}} \geq U_{1} | U_{1})}\Big]<\infty$
.
Let
![]() $S_{n}^{U} \;:\!=\; \sum_{j=1}^{n} \Delta_{j}^{U}$
and
$S_{n}^{U} \;:\!=\; \sum_{j=1}^{n} \Delta_{j}^{U}$
and
![]() $S_{n}^{L} \;:\!=\; \sum_{j=1}^{n} \Delta_{j}^{L}$
. We now state the main result of this subsection.
$S_{n}^{L} \;:\!=\; \sum_{j=1}^{n} \Delta_{j}^{L}$
. We now state the main result of this subsection.
Theorem 2.4. Assume ( H1 )–(H2). (i) If ( H5 ) and ( H8 ) hold, then
(ii) If ( H6 ) (or ( H7 )) and ( H9 ) hold, then
2.3. Proportion of time spent in supercritical and subcritical regimes
We now consider the proportion of time the process spends in the subcritical and supercritical regimes. To this end, for
![]() $n \geq 0$
, let
$n \geq 0$
, let
![]() $\chi_{n}^U \;:\!=\; \textbf{I}_{\cup_{j=1}^{\infty} [\nu_{j-1},\tau_{j})}(n)$
be the indicator function assuming value 1 if at time n the process is in the supercritical regime and 0 otherwise. Similarly, let
$\chi_{n}^U \;:\!=\; \textbf{I}_{\cup_{j=1}^{\infty} [\nu_{j-1},\tau_{j})}(n)$
be the indicator function assuming value 1 if at time n the process is in the supercritical regime and 0 otherwise. Similarly, let
![]() $\chi_{n}^L \;:\!=\; 1-\chi_{n}^U = \textbf{I}_{\cup_{j=1}^{\infty} [\tau_{j},\nu_{j})}(n)$
take value 1 if at time n the process is in the subcritical regime and 0 otherwise. Furthermore, let
$\chi_{n}^L \;:\!=\; 1-\chi_{n}^U = \textbf{I}_{\cup_{j=1}^{\infty} [\tau_{j},\nu_{j})}(n)$
take value 1 if at time n the process is in the subcritical regime and 0 otherwise. Furthermore, let
![]() $C_{n}^U \;:\!=\; \sum_{j=1}^{n} \chi_{j-1}^U$
and
$C_{n}^U \;:\!=\; \sum_{j=1}^{n} \chi_{j-1}^U$
and
![]() $C_{n}^L \;:\!=\; \sum_{j=1}^{n} \chi_{j-1}^L = n-C_{n}^U$
be the total time that the process spends in the supercritical and the subcritical regime, respectively, up to time
$C_{n}^L \;:\!=\; \sum_{j=1}^{n} \chi_{j-1}^L = n-C_{n}^U$
be the total time that the process spends in the supercritical and the subcritical regime, respectively, up to time
![]() $n-1$
. Let
$n-1$
. Let
denote the proportion of time the process spends in the supercritical and the subcritical regime. Our main result in this section is concerned with the central limit theorem for
![]() $\theta_{n}^{U}$
and
$\theta_{n}^{U}$
and
![]() $\theta_{n}^{L}$
. To this end, let
$\theta_{n}^{L}$
. To this end, let
Theorem 2.5.
Assume (
H1
)–(
H6
) (or (
H7
)) and (
H8
)–(
H9
). Then, for
![]() $T \in \{ L, U\}$
,
$T \in \{ L, U\}$
,
![]() $\theta_{n}^{T}$
converges a.s. to
$\theta_{n}^{T}$
converges a.s. to
![]() $\theta^{T}$
. Furthermore,
$\theta^{T}$
. Furthermore,
where
![]() $\eta^{2,T}$
is defined in (19).
$\eta^{2,T}$
is defined in (19).
We now use these results to describe the growth rate of the process in the supercritical and subcritical regime, as defined by their expectations (that is,
![]() $M^{U}$
and
$M^{U}$
and
![]() $M^{L}$
).
$M^{L}$
).
2.4. Offspring mean estimation
We begin by noticing that
![]() $Z_{\tau_{j}} \geq L_{U}+1$
and
$Z_{\tau_{j}} \geq L_{U}+1$
and
![]() $Z_{\tau_{j}+1}, \dots, Z_{\nu_{j}-1} \geq L_{0}$
are positive for all
$Z_{\tau_{j}+1}, \dots, Z_{\nu_{j}-1} \geq L_{0}$
are positive for all
![]() $j \in \mathbb{N}$
. However, there may be instances where
$j \in \mathbb{N}$
. However, there may be instances where
![]() $Z_{\nu_{j}}, \dots, Z_{\tau_{j}-1}$
could be zero. To avoid division by zero in (7) below, we let
$Z_{\nu_{j}}, \dots, Z_{\tau_{j}-1}$
could be zero. To avoid division by zero in (7) below, we let
![]() $\tilde{\chi}_{n}^{U} \;:\!=\; \chi_{n}^{U} \textbf{I}_{ \{ Z_{n} \geq 1 \}}$
,
$\tilde{\chi}_{n}^{U} \;:\!=\; \chi_{n}^{U} \textbf{I}_{ \{ Z_{n} \geq 1 \}}$
,
![]() $\tilde{C}_{n}^{U} \;:\!=\; \sum_{j=1}^{n} \tilde{\chi}_{j-1}^{U}$
, and use the convention that
$\tilde{C}_{n}^{U} \;:\!=\; \sum_{j=1}^{n} \tilde{\chi}_{j-1}^{U}$
, and use the convention that
![]() $0/0= 0 \cdot \infty=0$
. The generalized method-of-moments estimators of
$0/0= 0 \cdot \infty=0$
. The generalized method-of-moments estimators of
![]() $M^{U}$
and
$M^{U}$
and
![]() $M^{L}$
are given by
$M^{L}$
are given by
 \begin{equation} M_{n}^{U} \;:\!=\; \frac{1}{\tilde{C}_{n}^{U}} \sum_{j=1}^n \frac{Z_{j}-I_{j-1}^{U}}{Z_{j-1}} \tilde{\chi}_{j-1}^U \quad \text{ and } \quad M_{n}^L \;:\!=\; \frac{1}{C_{n}^{L}} \sum_{j=1}^n \frac{Z_{j}}{Z_{j-1}} \chi_{j-1}^L,\end{equation}
\begin{equation} M_{n}^{U} \;:\!=\; \frac{1}{\tilde{C}_{n}^{U}} \sum_{j=1}^n \frac{Z_{j}-I_{j-1}^{U}}{Z_{j-1}} \tilde{\chi}_{j-1}^U \quad \text{ and } \quad M_{n}^L \;:\!=\; \frac{1}{C_{n}^{L}} \sum_{j=1}^n \frac{Z_{j}}{Z_{j-1}} \chi_{j-1}^L,\end{equation}
where the last term is non-trivial whenever
![]() $C_{n}^{L} \geq 1$
, that is,
$C_{n}^{L} \geq 1$
, that is,
![]() $n \geq \tau_{1}+1$
. Our assumptions will involve first- and second-moment assumptions on the centered offspring means
$n \geq \tau_{1}+1$
. Our assumptions will involve first- and second-moment assumptions on the centered offspring means
![]() $\Big(\overline{P}_{n}^{T}-M^{T}\Big)$
and the centered offspring random variables
$\Big(\overline{P}_{n}^{T}-M^{T}\Big)$
and the centered offspring random variables
![]() $\Big( \xi_{n,i}^{T} - \overline{P}_{n}^{T}\Big)$
. To this end, we define the quantities
$\Big( \xi_{n,i}^{T} - \overline{P}_{n}^{T}\Big)$
. To this end, we define the quantities
![]() $\Lambda_{n,1}^{T,s} \;:\!=\; \Big\lvert\overline{P}_{n}^{T}-M^{T}\Big\rvert^{s}$
and
$\Lambda_{n,1}^{T,s} \;:\!=\; \Big\lvert\overline{P}_{n}^{T}-M^{T}\Big\rvert^{s}$
and
![]() $\Lambda_{n,2}^{T,s} \;:\!=\; \mathbb{E}\Big[\lvert\xi_{n,1}-\overline{P}_{n}^{T}\rvert^{s} | \Pi_{n}^{T}\Big]$
. Next, let
$\Lambda_{n,2}^{T,s} \;:\!=\; \mathbb{E}\Big[\lvert\xi_{n,1}-\overline{P}_{n}^{T}\rvert^{s} | \Pi_{n}^{T}\Big]$
. Next, let
![]() $\boldsymbol{M}_{n} \;:\!=\; \big(M_{n}^{U}, M_{n}^{L}\big)^{\top}$
,
$\boldsymbol{M}_{n} \;:\!=\; \big(M_{n}^{U}, M_{n}^{L}\big)^{\top}$
,
![]() $\boldsymbol{M} \;:\!=\; \big(M^{U}, M^{L}\big)^{\top}$
, and let
$\boldsymbol{M} \;:\!=\; \big(M^{U}, M^{L}\big)^{\top}$
, and let
![]() $\Sigma$
be the
$\Sigma$
be the
![]() $2 \times 2$
diagonal matrix with elements
$2 \times 2$
diagonal matrix with elements
where
![]() $\tilde{\mu}^{U} \;:\!=\; \mathbb{E}_{\pi^{L}}\big[\!\sum_{k=1}^{\tau_{1}} \tilde{\chi}_{k-1}^{U}\big]$
is the average length of supercritical regime, not taking into account the times at which the process is zero;
$\tilde{\mu}^{U} \;:\!=\; \mathbb{E}_{\pi^{L}}\big[\!\sum_{k=1}^{\tau_{1}} \tilde{\chi}_{k-1}^{U}\big]$
is the average length of supercritical regime, not taking into account the times at which the process is zero;
is the average proportion of time the process spends in the supercritical regime and is positive;
 \begin{align*}\tilde{A}^{U} \;:\!=\; \mathbb{E}_{\pi^{L}}\left[\sum_{k=1}^{\tau_{1}} \frac{\tilde{\chi}_{k-1}^{U}}{Z_{k-1}}\right]\end{align*}
\begin{align*}\tilde{A}^{U} \;:\!=\; \mathbb{E}_{\pi^{L}}\left[\sum_{k=1}^{\tau_{1}} \frac{\tilde{\chi}_{k-1}^{U}}{Z_{k-1}}\right]\end{align*}
is the average sum of
![]() $\frac{1}{Z_{n}}$
over a supercritical regime, discarding the times at which
$\frac{1}{Z_{n}}$
over a supercritical regime, discarding the times at which
![]() $Z_{n}$
is zero; and
$Z_{n}$
is zero; and
 \begin{align*}A^{L} \;:\!=\; \mathbb{E}_{\pi^{U}}\left[ \sum_{k=\tau_{1}+1}^{\nu_{1}} \frac{\chi_{k-1}^{L}}{Z_{k-1}} \right]\end{align*}
\begin{align*}A^{L} \;:\!=\; \mathbb{E}_{\pi^{U}}\left[ \sum_{k=\tau_{1}+1}^{\nu_{1}} \frac{\chi_{k-1}^{L}}{Z_{k-1}} \right]\end{align*}
is the average sum of
![]() $\frac{1}{Z_{n}}$
over a subcritical regime. Obviously,
$\frac{1}{Z_{n}}$
over a subcritical regime. Obviously,
![]() $0 \leq \tilde{\mu}^{U} \leq \mu^{U}$
. Finally, we recall that
$0 \leq \tilde{\mu}^{U} \leq \mu^{U}$
. Finally, we recall that
![]() $V_{1}^{T} = \mathbb{V}\Big[\overline{P}_{0}^{T}\Big]$
is the variance of the random offspring mean
$V_{1}^{T} = \mathbb{V}\Big[\overline{P}_{0}^{T}\Big]$
is the variance of the random offspring mean
![]() $\overline{P}_{0}^{T}$
and
$\overline{P}_{0}^{T}$
and
![]() $V_{2}^{T} = \mathbb{E}\Big[\overline{\overline{P}}_{0}^{T}\Big]$
is the expectation of the random offspring variance
$V_{2}^{T} = \mathbb{E}\Big[\overline{\overline{P}}_{0}^{T}\Big]$
is the expectation of the random offspring variance
![]() $\overline{\overline{P}}_{0}^{T}$
.
$\overline{\overline{P}}_{0}^{T}$
.
Theorem 2.6.
Assume (
H1
)–(
H6
) (or (
H7
)). (i) If
![]() $\mu^{T}<\infty$
and if
$\mu^{T}<\infty$
and if
![]() $\mathbb{E}\big[\Lambda_{0,i}^{T,s}\big]<\infty$
for some
$\mathbb{E}\big[\Lambda_{0,i}^{T,s}\big]<\infty$
for some
![]() $s > 1$
, where
$s > 1$
, where
![]() $i=1,2$
and
$i=1,2$
and
![]() $T \in \{L,U\}$
, then
$T \in \{L,U\}$
, then
![]() $\boldsymbol{M}_{n}$
is a strongly consistent estimator of
$\boldsymbol{M}_{n}$
is a strongly consistent estimator of
![]() $\boldsymbol{M}$
. (ii) If additionally for some
$\boldsymbol{M}$
. (ii) If additionally for some
![]() $\delta >0$
$\delta >0$
![]() $\mathbb{E}\big[\Lambda_{0,i}^{T,2+\delta}\big]<\infty$
for
$\mathbb{E}\big[\Lambda_{0,i}^{T,2+\delta}\big]<\infty$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $T \in \{L,U\}$
, then
$T \in \{L,U\}$
, then
Remark 2.1. In the fixed-environment case,
![]() $\overline{P}_{0}^{T} = M^{T}$
and
$\overline{P}_{0}^{T} = M^{T}$
and
![]() $\overline{\overline{P}}_{0}^{T} = V_{2}^{T}$
are deterministic constants. Therefore,
$\overline{\overline{P}}_{0}^{T} = V_{2}^{T}$
are deterministic constants. Therefore,
![]() $V_{1}^{T}=0$
, and
$V_{1}^{T}=0$
, and
![]() $\Sigma$
is the
$\Sigma$
is the
![]() $2 \times 2$
diagonal matrix with elements
$2 \times 2$
diagonal matrix with elements
3. Path properties of BPRET
In this section we provide the proofs of Theorems 2.1, 2.2, and 2.3, along with the required probability estimates. The proofs rely on the fact that both the environmental sequence and the thresholds are i.i.d. It follows that probability statements like
![]() $\mathbb{P}(Z_{\tau_{j+1}} = k | Z_{\nu_{j}}=i, \nu_{j}<\infty)$
and
$\mathbb{P}(Z_{\tau_{j+1}} = k | Z_{\nu_{j}}=i, \nu_{j}<\infty)$
and
![]() $\mathbb{P}(Z_{\nu_{j+1}}=i | Z_{\tau_{j+1}}=k, \tau_{j+1} < \infty)$
do not depend on the index j. This idea is made precise in Lemma A.1 in Appendix A.2 and will lead to time-homogeneity of
$\mathbb{P}(Z_{\nu_{j+1}}=i | Z_{\tau_{j+1}}=k, \tau_{j+1} < \infty)$
do not depend on the index j. This idea is made precise in Lemma A.1 in Appendix A.2 and will lead to time-homogeneity of
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
. As expected, this property does not depend on the process being strongly subcritical: Assumptions (
H1
) and (
H2′
) are more than enough. We denote by
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
. As expected, this property does not depend on the process being strongly subcritical: Assumptions (
H1
) and (
H2′
) are more than enough. We denote by
![]() $\mathbb{P}_{\delta_{i}^{L}}(\!\cdot\!)$
,
$\mathbb{P}_{\delta_{i}^{L}}(\!\cdot\!)$
,
![]() $\mathbb{E}_{\delta_{i}^{L}}[\!\cdot\!]$
,
$\mathbb{E}_{\delta_{i}^{L}}[\!\cdot\!]$
,
![]() $\mathbb{V}_{\delta_{i}^{L}}[\!\cdot\!]$
, and
$\mathbb{V}_{\delta_{i}^{L}}[\!\cdot\!]$
, and
![]() $\mathbb{C}_{\delta_{i}^{L}}[\cdot,\cdot]$
the probability, expectation, variance, and covariance conditionally on
$\mathbb{C}_{\delta_{i}^{L}}[\cdot,\cdot]$
the probability, expectation, variance, and covariance conditionally on
![]() $Z_{\nu_{0}} \sim \delta_{i}^{L}$
, where
$Z_{\nu_{0}} \sim \delta_{i}^{L}$
, where
![]() $\delta_{(\!\cdot\!)}^{L}$
is the restriction of the Dirac delta to
$\delta_{(\!\cdot\!)}^{L}$
is the restriction of the Dirac delta to
![]() $S^{L}$
. Similarly, when
$S^{L}$
. Similarly, when
![]() $\delta_{i}^{L}$
is replaced by
$\delta_{i}^{L}$
is replaced by
![]() $\delta_{i}^{U}$
in the above quantities, we understand that they are conditioned on
$\delta_{i}^{U}$
in the above quantities, we understand that they are conditioned on
![]() $Z_{\tau_{1}} \sim \delta_{i}^{U}$
, where
$Z_{\tau_{1}} \sim \delta_{i}^{U}$
, where
![]() $\delta_{(\!\cdot\!)}^{U}$
is the restriction of the Dirac delta to
$\delta_{(\!\cdot\!)}^{U}$
is the restriction of the Dirac delta to
![]() $S^{U}$
.
$S^{U}$
.
3.1. Extinction when immigration is zero
In this subsection, we provide the proof of Theorem 2.1, which is an adaptation of Theorem 1 of Athreya and Schuh [Reference Athreya and Schuh17] for BPRE. Recall that for this theorem there is no immigration in the supercritical regime, and hence the extinction time T is finite with probability one.
Proof of Theorem
2.1. For simplicity, set
![]() $\tau_{0} \;:\!=\; -1$
. We partition the sample space as
$\tau_{0} \;:\!=\; -1$
. We partition the sample space as
and show that (i)
![]() $\{ \tau_{j+1}=\infty, \tau_{j}<\infty \} \subset \{ \mathrm{T}<\infty \}$
for all
$\{ \tau_{j+1}=\infty, \tau_{j}<\infty \} \subset \{ \mathrm{T}<\infty \}$
for all
![]() $j \in \mathbb{N}_{0}$
and (ii)
$j \in \mathbb{N}_{0}$
and (ii)
![]() $\mathbb{P}\big(\!\cap_{j=1}^{\infty} \{ \tau_{j}< \infty \} \big)=0$
. First, we notice that if
$\mathbb{P}\big(\!\cap_{j=1}^{\infty} \{ \tau_{j}< \infty \} \big)=0$
. First, we notice that if
![]() $\tau_{j}<\infty$
, then
$\tau_{j}<\infty$
, then
![]() $\nu_{j}<\infty$
by Theorem 2.1 of Kersting and Vatutin [Reference Kersting and Vatutin16]. Thus,
$\nu_{j}<\infty$
by Theorem 2.1 of Kersting and Vatutin [Reference Kersting and Vatutin16]. Thus,
where
![]() $\{ Z_{n} \}_{n=\nu_{j}}^{\infty}$
is a supercritical BPRE until
$\{ Z_{n} \}_{n=\nu_{j}}^{\infty}$
is a supercritical BPRE until
![]() $U_{j+1}$
is reached. Since
$U_{j+1}$
is reached. Since
![]() $Z_{n} < U_{j+1}$
for all
$Z_{n} < U_{j+1}$
for all
![]() $n \geq \nu_{j}$
, (2.6) of Kersting and Vatutin [Reference Kersting and Vatutin16] yields that
$n \geq \nu_{j}$
, (2.6) of Kersting and Vatutin [Reference Kersting and Vatutin16] yields that
![]() $\lim_{n \to \infty} Z_{n} = 0$
a.s. and
$\lim_{n \to \infty} Z_{n} = 0$
a.s. and
![]() $\{ \tau_{j+1}=\infty, \tau_{j}<\infty \} \subset \{ \mathrm{T} < \infty \}$
. Turning to (ii), since the events
$\{ \tau_{j+1}=\infty, \tau_{j}<\infty \} \subset \{ \mathrm{T} < \infty \}$
. Turning to (ii), since the events
![]() $\{ \tau_{j} < \infty \}$
are nonincreasing,
$\{ \tau_{j} < \infty \}$
are nonincreasing,
![]() $\mathbb{P}\big(\!\cap_{j=1}^{\infty} \{ \tau_{j}< \infty\}\big)= \lim_{j \to \infty} \mathbb{P}(\tau_{j+1}< \infty)$
and
$\mathbb{P}\big(\!\cap_{j=1}^{\infty} \{ \tau_{j}< \infty\}\big)= \lim_{j \to \infty} \mathbb{P}(\tau_{j+1}< \infty)$
and
![]() $\mathbb{P}(\tau_{j+1}< \infty) = \mathbb{P}(\tau_{j+1} < \infty | \tau_{j}<\infty) \mathbb{P}(\tau_{j}<\infty)$
. Since
$\mathbb{P}(\tau_{j+1}< \infty) = \mathbb{P}(\tau_{j+1} < \infty | \tau_{j}<\infty) \mathbb{P}(\tau_{j}<\infty)$
. Since
![]() $\tau_{j}=\infty$
, if
$\tau_{j}=\infty$
, if
![]() $Z_{\nu_{j-1}}=0$
, it follows that
$Z_{\nu_{j-1}}=0$
, it follows that
 \begin{align*} \mathbb{P}(\tau_{j+1} < \infty | \tau_{j}<\infty) &\leq \mathbb{P}\big(\tau_{j+1} < \infty | \tau_{j}<\infty, Z_{\nu_{j-1}} \in [1,L_{U}]\big) \\[5pt] &\leq \max_{i=1,\dots,L_{U}} \mathbb{P}\big(\tau_{j+1} < \infty | \tau_{j}<\infty, Z_{\nu_{j-1}}=i\big) \\[5pt] &\leq 1-\min_{i=1,\dots,L_{U}} \mathbb{P}\big(Z_{\tau_{j}+1} = 0 | \tau_{j}<\infty, Z_{\nu_{j-1}}=i\big).\end{align*}
\begin{align*} \mathbb{P}(\tau_{j+1} < \infty | \tau_{j}<\infty) &\leq \mathbb{P}\big(\tau_{j+1} < \infty | \tau_{j}<\infty, Z_{\nu_{j-1}} \in [1,L_{U}]\big) \\[5pt] &\leq \max_{i=1,\dots,L_{U}} \mathbb{P}\big(\tau_{j+1} < \infty | \tau_{j}<\infty, Z_{\nu_{j-1}}=i\big) \\[5pt] &\leq 1-\min_{i=1,\dots,L_{U}} \mathbb{P}\big(Z_{\tau_{j}+1} = 0 | \tau_{j}<\infty, Z_{\nu_{j-1}}=i\big).\end{align*}
Lemma A.1 yields that for all
![]() $k \in S_{B}^{U}$
,
$k \in S_{B}^{U}$
,
Also, for all
![]() $j \geq 1$
,
$j \geq 1$
,
 \begin{align*} \mathbb{P}\big(Z_{\tau_{j}+1}=0 | \tau_{j}<\infty, Z_{\tau_{j}}=k\big) &=\mathbb{P} \big(\!\cap_{i=1}^{k} \big\{ \xi_{\tau_{j},i}^{L}=0 \big\} | \tau_{j}<\infty \big) \\[5pt] &=\sum_{n=1}^{\infty} \mathbb{P} \big(\!\cap_{i=1}^{k} \big\{ \xi_{n,i}^{L}=0 \big\} | \tau_{j}=n \big) \mathbb{P}(\tau_{j}=n) \\[5pt] &= \mathbb{P}\big(\xi_{0,1}^{L}=0\big)^{k}.\end{align*}
\begin{align*} \mathbb{P}\big(Z_{\tau_{j}+1}=0 | \tau_{j}<\infty, Z_{\tau_{j}}=k\big) &=\mathbb{P} \big(\!\cap_{i=1}^{k} \big\{ \xi_{\tau_{j},i}^{L}=0 \big\} | \tau_{j}<\infty \big) \\[5pt] &=\sum_{n=1}^{\infty} \mathbb{P} \big(\!\cap_{i=1}^{k} \big\{ \xi_{n,i}^{L}=0 \big\} | \tau_{j}=n \big) \mathbb{P}(\tau_{j}=n) \\[5pt] &= \mathbb{P}\big(\xi_{0,1}^{L}=0\big)^{k}.\end{align*}
Multiplying by
![]() $\mathbb{P}\big(Z_{\tau_{j}+1}=0 | \tau_{j}<\infty, Z_{\tau_{j}}=k\big)$
and
$\mathbb{P}\big(Z_{\tau_{j}+1}=0 | \tau_{j}<\infty, Z_{\tau_{j}}=k\big)$
and
![]() $\mathbb{P}\big(Z_{\tau_{1}+1}=0 | \tau_{1}<\infty, Z_{\tau_{1}}=k\big)$
and summing over
$\mathbb{P}\big(Z_{\tau_{1}+1}=0 | \tau_{1}<\infty, Z_{\tau_{1}}=k\big)$
and summing over
![]() $k \geq L_{U}+1$
in (8), we obtain that
$k \geq L_{U}+1$
in (8), we obtain that
 \begin{align*} \mathbb{P}\big(Z_{\tau_{j}+1}=0 | \tau_{j}<\infty, Z_{\nu_{j-1}}=i\big) &=\mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}+1}=0 | \tau_{1} < \infty\big) \\[5pt] &=\sum_{k=L_{U}+1}^{\infty} \mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}}=k | \tau_{1} < \infty\big) \mathbb{P}\big(\xi_{0,1}^{L}=0\big)^{k}.\end{align*}
\begin{align*} \mathbb{P}\big(Z_{\tau_{j}+1}=0 | \tau_{j}<\infty, Z_{\nu_{j-1}}=i\big) &=\mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}+1}=0 | \tau_{1} < \infty\big) \\[5pt] &=\sum_{k=L_{U}+1}^{\infty} \mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}}=k | \tau_{1} < \infty\big) \mathbb{P}\big(\xi_{0,1}^{L}=0\big)^{k}.\end{align*}
Set
![]() $\underline{p} \;:\!=\; \min_{i=1,\dots,L_{U}} p_{i}$
, where
$\underline{p} \;:\!=\; \min_{i=1,\dots,L_{U}} p_{i}$
, where
![]() $p_{i} \;:\!=\; \mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}+1}=0 | \tau_{1} < \infty\big)$
. Since
$p_{i} \;:\!=\; \mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}+1}=0 | \tau_{1} < \infty\big)$
. Since
![]() $\mathbb{P}\big(\xi_{0,1}^{L}=0\big)>0$
and
$\mathbb{P}\big(\xi_{0,1}^{L}=0\big)>0$
and
![]() $\mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}}=k | \tau_{1} < \infty\big)>0$
for some k, we have that
$\mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}}=k | \tau_{1} < \infty\big)>0$
for some k, we have that
![]() $p_{i}>0$
and
$p_{i}>0$
and
![]() $\underline{p}>0$
. Hence,
$\underline{p}>0$
. Hence,
![]() $\mathbb{P}(\tau_{j+1}< \infty) \leq (1-\underline{p}) \mathbb{P}(\tau_{j}< \infty)$
. Iterating the above argument, it follows that
$\mathbb{P}(\tau_{j+1}< \infty) \leq (1-\underline{p}) \mathbb{P}(\tau_{j}< \infty)$
. Iterating the above argument, it follows that
![]() $\mathbb{P}(\tau_{j+1}< \infty) \leq \big(1-\underline{p}\big)^{j} \mathbb{P}(\tau_{1}<\infty)$
, yielding
$\mathbb{P}(\tau_{j+1}< \infty) \leq \big(1-\underline{p}\big)^{j} \mathbb{P}(\tau_{1}<\infty)$
, yielding
![]() $\lim_{j \to \infty} \mathbb{P}(\tau_{j+1}< \infty)=0$
.
$\lim_{j \to \infty} \mathbb{P}(\tau_{j+1}< \infty)=0$
.
3.2. Markov property at crossing times
Proof of Theorem
2.2. We begin by proving (i). We first notice that since
![]() $\{U_{j}\}_{j=1}^{\infty}$
are i.i.d. random variables with unbounded support
$\{U_{j}\}_{j=1}^{\infty}$
are i.i.d. random variables with unbounded support
![]() $S_{B}^{U}$
,
$S_{B}^{U}$
,
![]() $\limsup_{j \rightarrow \infty} U_{j} = \infty$
with probability one. Next, observe that along the subsequence
$\limsup_{j \rightarrow \infty} U_{j} = \infty$
with probability one. Next, observe that along the subsequence
![]() $\{\tau_{j}\}_{j=1}^{\infty}$
,
$\{\tau_{j}\}_{j=1}^{\infty}$
,
![]() $Z_{\tau_{j}} \ge U_{j}$
. Hence,
$Z_{\tau_{j}} \ge U_{j}$
. Hence,
![]() $\limsup_{n \rightarrow \infty} Z_{n} =\infty$
. On the other hand, along the subsequence
$\limsup_{n \rightarrow \infty} Z_{n} =\infty$
. On the other hand, along the subsequence
![]() $\{\nu_{j} \}_{j=1}^{\infty}$
, we have
$\{\nu_{j} \}_{j=1}^{\infty}$
, we have
![]() $Z_{\nu_{j}} \le L_{j}$
. Thus,
$Z_{\nu_{j}} \le L_{j}$
. Thus,
![]() $0 \le \liminf_{j\rightarrow \infty} Z_{j} \le L_U<\infty$
. It follows that
$0 \le \liminf_{j\rightarrow \infty} Z_{j} \le L_U<\infty$
. It follows that
![]() $\{ Z_{n} \}_{n=0}^{\infty}$
is recurrent in the sense of Definition 2.1. Turning to (ii), we first notice that, since
$\{ Z_{n} \}_{n=0}^{\infty}$
is recurrent in the sense of Definition 2.1. Turning to (ii), we first notice that, since
![]() $Z_{0} \leq L_{U}$
,
$Z_{0} \leq L_{U}$
,
![]() $Z_{\nu_{j}} \leq L_{j} \leq L_{U}$
, and
$Z_{\nu_{j}} \leq L_{j} \leq L_{U}$
, and
![]() $Z_{\tau_{j}} \geq U_{j} \geq L_{U}+1$
for all
$Z_{\tau_{j}} \geq U_{j} \geq L_{U}+1$
for all
![]() $j \geq 1$
, the state spaces
$j \geq 1$
, the state spaces
![]() $S^{L}$
of
$S^{L}$
of
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
![]() $S^{U}$
of
$S^{U}$
of
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
are included in
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
are included in
![]() $S^{L}$
and
$S^{L}$
and
![]() $S^{U}$
, respectively. We now establish the Markov property of
$S^{U}$
, respectively. We now establish the Markov property of
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
. For all
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
. For all
![]() $j \geq 0$
,
$j \geq 0$
,
![]() $k \in S^{L}$
, and
$k \in S^{L}$
, and
![]() $i_{0},i_{1},\dots,i_{j} \in S^{L}$
, we consider the probability
$i_{0},i_{1},\dots,i_{j} \in S^{L}$
, we consider the probability
![]() $\mathbb{P}(Z_{\nu_{j+1}}=k | Z_{\nu_{0}}=i_{0},\dots,Z_{\nu_{j}}=i_{j})$
. By the law of total expectation, this is equal to
$\mathbb{P}(Z_{\nu_{j+1}}=k | Z_{\nu_{0}}=i_{0},\dots,Z_{\nu_{j}}=i_{j})$
. By the law of total expectation, this is equal to
Now, setting
![]() $A_{\nu_{j},s}(u) \;:\!=\; \{ Z_{\nu_{j}+s} \geq u, Z_{\nu_{j}+s-1} <u, \dots, Z_{\nu_{j}+1} < u \}$
,
$A_{\nu_{j},s}(u) \;:\!=\; \{ Z_{\nu_{j}+s} \geq u, Z_{\nu_{j}+s-1} <u, \dots, Z_{\nu_{j}+1} < u \}$
,
![]() $B_{\nu_{j},s,t}(l) \;:\!=\; \{ Z_{\nu_{j}+t}=k, Z_{\nu_{j}+t-1} > l, \dots, Z_{\nu_{j}+s+1} > l \}$
, we have that
$B_{\nu_{j},s,t}(l) \;:\!=\; \{ Z_{\nu_{j}+t}=k, Z_{\nu_{j}+t-1} > l, \dots, Z_{\nu_{j}+s+1} > l \}$
, we have that
 \begin{align*} &\mathbb{P}\big(Z_{\nu_{j+1}}=k | Z_{\nu_{0}}=i_{0},\dots,Z_{\nu_{j}}=i_{j},L_{j+1},U_{j+1},\pi^{L}, \pi^{U} \big) \\[5pt] =\ & \sum_{s=1}^{\infty} \sum_{t=s+1}^{\infty} \mathbb{P}\big(A_{\nu_{j},s}(U_{j+1}) | Z_{\nu_{j}}=i_{j},U_{j+1},\pi^{U}\big) \mathbb{P}\big( B_{\nu_{j},s,t}(L_{j+1}) | A_{\nu_{j},s}, L_{j+1},\pi^{L}\big) \\[5pt] =\ &\mathbb{P}\big(Z_{\nu_{j+1}}=k | Z_{\nu_{j}}=i_{j},L_{j+1},U_{j+1},\pi^{L}, \pi^{U}\big),\end{align*}
\begin{align*} &\mathbb{P}\big(Z_{\nu_{j+1}}=k | Z_{\nu_{0}}=i_{0},\dots,Z_{\nu_{j}}=i_{j},L_{j+1},U_{j+1},\pi^{L}, \pi^{U} \big) \\[5pt] =\ & \sum_{s=1}^{\infty} \sum_{t=s+1}^{\infty} \mathbb{P}\big(A_{\nu_{j},s}(U_{j+1}) | Z_{\nu_{j}}=i_{j},U_{j+1},\pi^{U}\big) \mathbb{P}\big( B_{\nu_{j},s,t}(L_{j+1}) | A_{\nu_{j},s}, L_{j+1},\pi^{L}\big) \\[5pt] =\ &\mathbb{P}\big(Z_{\nu_{j+1}}=k | Z_{\nu_{j}}=i_{j},L_{j+1},U_{j+1},\pi^{L}, \pi^{U}\big),\end{align*}
where in the second line we have used that
![]() $\{ Z_{n} \}_{n=\nu_{j}}^{\infty}$
is a supercritical BPRE with immigration until it crosses the threshold
$\{ Z_{n} \}_{n=\nu_{j}}^{\infty}$
is a supercritical BPRE with immigration until it crosses the threshold
![]() $U_{j+1}$
at time
$U_{j+1}$
at time
![]() $\tau_{j+1}=\nu_{j}+s$
, and similarly
$\tau_{j+1}=\nu_{j}+s$
, and similarly
![]() $\{ Z_{n} \}_{n=\tau_{j+1}}^{\infty}$
is a subcritical BPRE until it crosses the threshold
$\{ Z_{n} \}_{n=\tau_{j+1}}^{\infty}$
is a subcritical BPRE until it crosses the threshold
![]() $L_{j+1}$
at time
$L_{j+1}$
at time
![]() $\nu_{j+1}=\nu_{j}+t$
. By taking the expectation on both sides, we obtain that
$\nu_{j+1}=\nu_{j}+t$
. By taking the expectation on both sides, we obtain that
Turning to the time-homogeneity property, we obtain from Lemma A.1(iii) that
 \begin{align*} \mathbb{P}\big(Z_{\nu_{j+1}}=k | Z_{\nu_{j}}=i_{j}\big) &= \sum_{l=L_{U}+1}^{\infty} \mathbb{P}\big(Z_{\nu_{j+1}}=k | Z_{\tau_{j+1}}=l\big) \mathbb{P}\big(Z_{\tau_{j+1}}=l | Z_{\nu_{j}}=i_{j}\big) \\[5pt] &= \sum_{l=L_{U}+1}^{\infty} \mathbb{P}\big(Z_{\nu_{1}}=k | Z_{\tau_{1}}=l\big) \mathbb{P}\big(Z_{\tau_{1}}=l | Z_{\nu_{0}}=i_{j}\big) \\[5pt] &=\mathbb{P}\big(Z_{\nu_{1}}=k | Z_{\nu_{0}}=i_{j}\big).\end{align*}
\begin{align*} \mathbb{P}\big(Z_{\nu_{j+1}}=k | Z_{\nu_{j}}=i_{j}\big) &= \sum_{l=L_{U}+1}^{\infty} \mathbb{P}\big(Z_{\nu_{j+1}}=k | Z_{\tau_{j+1}}=l\big) \mathbb{P}\big(Z_{\tau_{j+1}}=l | Z_{\nu_{j}}=i_{j}\big) \\[5pt] &= \sum_{l=L_{U}+1}^{\infty} \mathbb{P}\big(Z_{\nu_{1}}=k | Z_{\tau_{1}}=l\big) \mathbb{P}\big(Z_{\tau_{1}}=l | Z_{\nu_{0}}=i_{j}\big) \\[5pt] &=\mathbb{P}\big(Z_{\nu_{1}}=k | Z_{\nu_{0}}=i_{j}\big).\end{align*}
The proof for
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
is similar.
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
is similar.
3.3. Uniform ergodicity of
 $\{Z_{\nu_{\boldsymbol{j}}}\}_{\boldsymbol{j}=0}^{\infty}$
and
$\{Z_{\nu_{\boldsymbol{j}}}\}_{\boldsymbol{j}=0}^{\infty}$
and
 $\{ Z_{\tau_{\boldsymbol{j}}} \}_{\boldsymbol{j}=1}^{\infty}$
$\{ Z_{\tau_{\boldsymbol{j}}} \}_{\boldsymbol{j}=1}^{\infty}$
In this subsection we prove Theorem 2.3. The proof relies on the following lemma. We denote by
![]() $p_{ik}^{L}(j)=\mathbb{P}_{\delta_{i}^{L}}(Z_{\nu_{j}}=k)$
,
$p_{ik}^{L}(j)=\mathbb{P}_{\delta_{i}^{L}}(Z_{\nu_{j}}=k)$
,
![]() $i,k \in S^{L}$
, and
$i,k \in S^{L}$
, and
![]() $p_{ik}^{U}(j)=\mathbb{P}_{\delta_{i}^{U}}(Z_{\tau_{j+1}}=k)$
,
$p_{ik}^{U}(j)=\mathbb{P}_{\delta_{i}^{U}}(Z_{\tau_{j+1}}=k)$
,
![]() $i,k \in S^{U}$
, the j-step transition probability of the (time-homogeneous) Markov chains
$i,k \in S^{U}$
, the j-step transition probability of the (time-homogeneous) Markov chains
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
. For
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
. For
![]() $j=1$
, we also write
$j=1$
, we also write
![]() $p_{ik}^{L}=p_{ik}^{L}(1)$
and
$p_{ik}^{L}=p_{ik}^{L}(1)$
and
![]() $p_{ik}^{U}=p_{ik}^{U}(1)$
. Finally, let
$p_{ik}^{U}=p_{ik}^{U}(1)$
. Finally, let
![]() $p_{i}^{L}(j)=\{ p_{ik}^{L}(j) \}_{k \in S^{L}}$
and
$p_{i}^{L}(j)=\{ p_{ik}^{L}(j) \}_{k \in S^{L}}$
and
![]() $p_{i}^{U}(j)=\{ p_{ik}^{U}(j) \}_{k \in S^{U}}$
be the j-step transition probability of the Markov chains
$p_{i}^{U}(j)=\{ p_{ik}^{U}(j) \}_{k \in S^{U}}$
be the j-step transition probability of the Markov chains
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
from state
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
from state
![]() $i \in S^{L}$
(resp.
$i \in S^{L}$
(resp.
![]() $i \in S^{U}$
).
$i \in S^{U}$
).
Lemma 3.1.
Assume (
H1
)–(
H4
). Then (i) if (
H5
) also holds, then
![]() $p_{ik}^{L} \geq \underline{p}^{L}>0$
for all
$p_{ik}^{L} \geq \underline{p}^{L}>0$
for all
![]() $i,k \in S^{L}$
. Also, (ii) if 2 (or 3) holds, then
$i,k \in S^{L}$
. Also, (ii) if 2 (or 3) holds, then
![]() $p_{ik}^{U} \geq \underline{p}_{k}^{U}>0$
for all
$p_{ik}^{U} \geq \underline{p}_{k}^{U}>0$
for all
![]() $i,k \in S^{U}$
.
$i,k \in S^{U}$
.
Proof of Lemma
3.1. The idea of proof is to establish a lower bound on
![]() $p_{ik}^{L}$
and
$p_{ik}^{L}$
and
![]() $p_{ik}^{U}$
using (9) and (10) below, respectively. We begin by proving (i). Using Assumption (
H5
), let A be a measurable subset of
$p_{ik}^{U}$
using (9) and (10) below, respectively. We begin by proving (i). Using Assumption (
H5
), let A be a measurable subset of
![]() $\mathcal{P}$
satisfying
$\mathcal{P}$
satisfying
![]() $\mathbb{P}_{E^{L}}\big(\Pi_{0}^{L} \in A\big)>0$
and
$\mathbb{P}_{E^{L}}\big(\Pi_{0}^{L} \in A\big)>0$
and
![]() $P_{0,r}^{L} > 0$
for
$P_{0,r}^{L} > 0$
for
![]() $r=0,1$
and
$r=0,1$
and
![]() $\Pi_{0}^{L} \in A$
. By the law of total expectation,
$\Pi_{0}^{L} \in A$
. By the law of total expectation,
Since
![]() $\mathbb{P}\big(Z_{\nu_{1}}=k | Z_{\tau_{1}}, L_{1},\pi^{L}\big)=0$
on the event
$\mathbb{P}\big(Z_{\nu_{1}}=k | Z_{\tau_{1}}, L_{1},\pi^{L}\big)=0$
on the event
![]() $\{L_{1} < k\}$
, it follows that
$\{L_{1} < k\}$
, it follows that
Now, notice that on the event
![]() $\{L_{1} \geq k\}$
, the term
$\{L_{1} \geq k\}$
, the term
![]() $\mathbb{P}\big(Z_{\nu_{1}}=k | Z_{\tau_{1}}, L_{1},\pi^{L}\big)$
is bounded below by the probability of reaching state k from
$\mathbb{P}\big(Z_{\nu_{1}}=k | Z_{\tau_{1}}, L_{1},\pi^{L}\big)$
is bounded below by the probability of reaching state k from
![]() $Z_{\tau_{1}}$
in one step; that is,
$Z_{\tau_{1}}$
in one step; that is,
The right-hand side of the above inequality is bounded below by the probability that the first k individuals have exactly one offspring and the remaining
![]() $Z_{\tau_{1}}-k$
have no offspring; that is,
$Z_{\tau_{1}}-k$
have no offspring; that is,
 \begin{equation*} \textbf{I}_{\{L_{1} \geq k\}} \prod_{r=1}^{k} \mathbb{P}\big(\xi_{\tau_{1},r}^{L}=1 | \Pi_{\tau_{1}}^{L}\big) \prod_{r=k+1}^{Z_{\tau_{1}}} \mathbb{P}\big(\xi_{\tau_{1},r}^{L}=0 | \Pi_{\tau_{1}}^{L}\big).\end{equation*}
\begin{equation*} \textbf{I}_{\{L_{1} \geq k\}} \prod_{r=1}^{k} \mathbb{P}\big(\xi_{\tau_{1},r}^{L}=1 | \Pi_{\tau_{1}}^{L}\big) \prod_{r=k+1}^{Z_{\tau_{1}}} \mathbb{P}\big(\xi_{\tau_{1},r}^{L}=0 | \Pi_{\tau_{1}}^{L}\big).\end{equation*}
Once again, using that, conditional on the environment
![]() $\Pi_{\tau_{1}}^{L}$
, the
$\Pi_{\tau_{1}}^{L}$
, the
![]() $\xi_{\tau_{1},r}^{L}$
are i.i.d., this is equal to
$\xi_{\tau_{1},r}^{L}$
are i.i.d., this is equal to
Since
![]() $\textbf{I}_{\{\Pi_{\tau_{1}}^{L} \in A\}} \leq 1$
and
$\textbf{I}_{\{\Pi_{\tau_{1}}^{L} \in A\}} \leq 1$
and
![]() $\{L_{1} \geq k\} \supset \{L_{1}=L_{U}\}$
because
$\{L_{1} \geq k\} \supset \{L_{1}=L_{U}\}$
because
![]() $k \leq L_{U}$
, the last term is bounded below by
$k \leq L_{U}$
, the last term is bounded below by
Finally, again using that the
![]() $\Pi_{n}^{L}$
are i.i.d., and taking the expectation
$\Pi_{n}^{L}$
are i.i.d., and taking the expectation
![]() $\mathbb{E}_{\delta_{i}^{L}}[\!\cdot\!]$
as in (9), we obtain that
$\mathbb{E}_{\delta_{i}^{L}}[\!\cdot\!]$
as in (9), we obtain that
![]() $p_{ik}^{L} \geq \underline{p}_{ik}^{L}$
, where
$p_{ik}^{L} \geq \underline{p}_{ik}^{L}$
, where
Notice that
![]() $\underline{p}_{k}^{L}$
is positive, because
$\underline{p}_{k}^{L}$
is positive, because
![]() $\mathbb{P}(L_{1}=L_{U}) > 0$
,
$\mathbb{P}(L_{1}=L_{U}) > 0$
,
![]() $\mathbb{P}_{E^{L}}\big(\Pi_{0}^{L} \in A\big)>0$
,
$\mathbb{P}_{E^{L}}\big(\Pi_{0}^{L} \in A\big)>0$
,
![]() $P_{0,r}^{L} > 0$
for
$P_{0,r}^{L} > 0$
for
![]() $r=0,1$
, and
$r=0,1$
, and
![]() $\Pi_{0}^{L} \in A$
, and the environments
$\Pi_{0}^{L} \in A$
, and the environments
![]() $\Pi_{n}^{L}$
are i.i.d. Finally, since
$\Pi_{n}^{L}$
are i.i.d. Finally, since
![]() $S^{L}$
is finite,
$S^{L}$
is finite,
![]() $\underline{p}^{L} \;:\!=\; \min_{i,k \in S^{L}} \underline{p}_{ik}^{L} > 0$
.
$\underline{p}^{L} \;:\!=\; \min_{i,k \in S^{L}} \underline{p}_{ik}^{L} > 0$
.
We now turn to the proof of (ii), which is similar to the proof of (i). Using (
H6
), let A and B be measurable subsets of
![]() $\mathcal{P} \times \mathcal{P}$
satisfying the following conditions:
$\mathcal{P} \times \mathcal{P}$
satisfying the following conditions:
-
(a)
 $\mathbb{P}_{E^{U}}\big( \Pi_{0}^{U} \in A\big) > 0$
and
$\mathbb{P}_{E^{U}}\big( \Pi_{0}^{U} \in A\big) > 0$
and
 $Q_{0,0}^{U}>0$
,
$Q_{0,0}^{U}>0$
,
 $P_{0,r}^{U}>0$
for all
$P_{0,r}^{U}>0$
for all
 $r \in \mathbb{N}_{0}$
and
$r \in \mathbb{N}_{0}$
and
 $\Pi_{0}^{U} \in A$
; and
$\Pi_{0}^{U} \in A$
; and -
(b)
 $\mathbb{P}_{E^{U}}\big( \Pi_{0}^{U} \in B\big) > 0$
and
$\mathbb{P}_{E^{U}}\big( \Pi_{0}^{U} \in B\big) > 0$
and
 $Q_{0,s}^{U}>0$
for some (fixed)
$Q_{0,s}^{U}>0$
for some (fixed)
 $s \in \{1,\dots, L_{u}\}$
and
$s \in \{1,\dots, L_{u}\}$
and
 $\Pi_{0}^{U} \in B$
.
$\Pi_{0}^{U} \in B$
.
Again using the law of total expectation, we obtain
Since
![]() $\mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big)=0$
on the event
$\mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big)=0$
on the event
![]() $\{U_{2} > k\}$
, it follows that
$\{U_{2} > k\}$
, it follows that
 \begin{equation} \mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big) = \sum_{z=0}^{L_{U}} \mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big) \textbf{I}_{\{U_{2} \leq k\}} I_{\{Z_{\nu_{1}}=z\}}.\end{equation}
\begin{equation} \mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big) = \sum_{z=0}^{L_{U}} \mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big) \textbf{I}_{\{U_{2} \leq k\}} I_{\{Z_{\nu_{1}}=z\}}.\end{equation}
If
![]() $U_{2} \leq k$
and
$U_{2} \leq k$
and
![]() $Z_{\nu_{1}}=z>0$
, then
$Z_{\nu_{1}}=z>0$
, then
![]() $\mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big)$
is bounded below by the probability that z individuals have a total of exactly k offspring and no immigration occurs; that is,
$\mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big)$
is bounded below by the probability that z individuals have a total of exactly k offspring and no immigration occurs; that is,
 \begin{align*} &\mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big) \textbf{I}_{\{U_{2} \leq k\}} I_{\{Z_{\nu_{1}}=z\}} \\[5pt] \geq &\mathbb{P}\Bigg( \sum_{r=1}^{z} \xi_{\nu_{1},r}^{U}=k, I_{\nu_{1}}^{U}=0 | Z_{\nu_{1}}, U_{2},\pi^{U}\Bigg) \textbf{I}_{\{U_{2} \leq k\}} I_{\{Z_{\nu_{1}}=z\}}.\end{align*}
\begin{align*} &\mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big) \textbf{I}_{\{U_{2} \leq k\}} I_{\{Z_{\nu_{1}}=z\}} \\[5pt] \geq &\mathbb{P}\Bigg( \sum_{r=1}^{z} \xi_{\nu_{1},r}^{U}=k, I_{\nu_{1}}^{U}=0 | Z_{\nu_{1}}, U_{2},\pi^{U}\Bigg) \textbf{I}_{\{U_{2} \leq k\}} I_{\{Z_{\nu_{1}}=z\}}.\end{align*}
The right-hand side of the above inequality is bounded below by the probability that the first
![]() $z_{1} \;:\!=\; (k_{1}+1)z-k$
individuals have
$z_{1} \;:\!=\; (k_{1}+1)z-k$
individuals have
![]() $k_{1} \;:\!=\; \lfloor \frac{k}{z} \rfloor$
offspring and the last
$k_{1} \;:\!=\; \lfloor \frac{k}{z} \rfloor$
offspring and the last
![]() $z_{2} \;:\!=\; z-z_{1}$
individuals have
$z_{2} \;:\!=\; z-z_{1}$
individuals have
![]() $k_{2} \;:\!=\; k_{1}+1$
offspring (indeed
$k_{2} \;:\!=\; k_{1}+1$
offspring (indeed
![]() $k_{1} z_{1} + k_{2} z_{2}=k$
) and no immigration occurs—that is, by
$k_{1} z_{1} + k_{2} z_{2}=k$
) and no immigration occurs—that is, by
Using that, conditional on the environment,
![]() $\Pi_{\nu_{1}}^{U}$
,
$\Pi_{\nu_{1}}^{U}$
,
![]() $\xi_{\nu_{1},r}^{U}$
are i.i.d., the above is equal to
$\xi_{\nu_{1},r}^{U}$
are i.i.d., the above is equal to
Next, if
![]() $U_{2} \leq k$
and
$U_{2} \leq k$
and
![]() $Z_{\nu_{1}}=z=0$
, then
$Z_{\nu_{1}}=z=0$
, then
![]() $\mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big)$
is bounded below by the probability
$\mathbb{P}\big(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U}\big)$
is bounded below by the probability
![]() $\mathbb{P}\big(Z_{\tau_{2}}=k, \tau_{2}=\nu_{1}+2 | Z_{\nu_{1}}, U_{2},\pi^{U}\big)$
. Now, this probability is bounded below by the probability that there are s immigrants at time
$\mathbb{P}\big(Z_{\tau_{2}}=k, \tau_{2}=\nu_{1}+2 | Z_{\nu_{1}}, U_{2},\pi^{U}\big)$
. Now, this probability is bounded below by the probability that there are s immigrants at time
![]() $\nu_{1}+1$
, these immigrants have a total of exactly k offspring, and no immigration occurs at time
$\nu_{1}+1$
, these immigrants have a total of exactly k offspring, and no immigration occurs at time
![]() $\nu_{1}+2$
—that is, by
$\nu_{1}+2$
—that is, by
 \begin{equation*} \mathbb{P} \Bigg(I_{\nu_{1}}^{U}=s, \sum_{r=1}^{s} \xi_{\nu_{1}+1,r}^{U}=k, I_{\nu_{1}+1}^{U}=0 | Z_{\nu_{1}}, U_{2},\pi^{U} \Bigg) \textbf{I}_{\{U_{2} \leq k\}} I_{\{Z_{\nu_{1}}=0\}}.\end{equation*}
\begin{equation*} \mathbb{P} \Bigg(I_{\nu_{1}}^{U}=s, \sum_{r=1}^{s} \xi_{\nu_{1}+1,r}^{U}=k, I_{\nu_{1}+1}^{U}=0 | Z_{\nu_{1}}, U_{2},\pi^{U} \Bigg) \textbf{I}_{\{U_{2} \leq k\}} I_{\{Z_{\nu_{1}}=0\}}.\end{equation*}
As before, this last probability is bounded below by the probability that
![]() $s_{1} \;:\!=\; (t_{1}+1)s-k$
individuals have
$s_{1} \;:\!=\; (t_{1}+1)s-k$
individuals have
![]() $t_{1} \;:\!=\; \lfloor \frac{k}{s} \rfloor$
offspring and
$t_{1} \;:\!=\; \lfloor \frac{k}{s} \rfloor$
offspring and
![]() $s_{2} \;:\!=\; s-s_{1}$
individuals have
$s_{2} \;:\!=\; s-s_{1}$
individuals have
![]() $t_{2} \;:\!=\; t_{1}+1$
offspring. Thus, the above probability is bounded below by
$t_{2} \;:\!=\; t_{1}+1$
offspring. Thus, the above probability is bounded below by
Combining (11), (12), and (13) and using that
![]() $\textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in A\}}, \textbf{I}_{\{\Pi_{\nu_{1}+1}^{U} \in A\}}, \textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in B\}} \leq 1$
, we obtain that
$\textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in A\}}, \textbf{I}_{\{\Pi_{\nu_{1}+1}^{U} \in A\}}, \textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in B\}} \leq 1$
, we obtain that
![]() $\mathbb{P}(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U})$
is bounded below by
$\mathbb{P}(Z_{\tau_{2}}=k | Z_{\nu_{1}}, U_{2},\pi^{U})$
is bounded below by
 \begin{align*} & \textbf{I}_{\{ U_{2} \leq k\}} \sum_{z=1}^{L_{U}} \textbf{I}_{\{Z_{\nu_{1}} = z\} } \Big(P_{\nu_{1},k_{1}}^{U}\Big)^{z_{1}} \Big(P_{\nu_{1},k_{2}}^{U}\Big)^{z_{2}} Q_{\nu_{1},0}^{U} \textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in A\}} \\[5pt] +\ &\textbf{I}_{\{U_{2} \leq k\}} \textbf{I}_{\{Z_{\nu_{1}} = 0\} } Q_{\nu_{1},s}^{U} \Big(P_{\nu_{1}+1,t_{1}}^{U}\Big)^{s_{1}} \Big(P_{\nu_{1}+1,t_{2}}^{U}\Big)^{s_{2}} Q_{\nu_{1}+1,0}^{U} \textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in B\}} \textbf{I}_{\{\Pi_{\nu_{1}+1}^{U} \in A\}}.\end{align*}
\begin{align*} & \textbf{I}_{\{ U_{2} \leq k\}} \sum_{z=1}^{L_{U}} \textbf{I}_{\{Z_{\nu_{1}} = z\} } \Big(P_{\nu_{1},k_{1}}^{U}\Big)^{z_{1}} \Big(P_{\nu_{1},k_{2}}^{U}\Big)^{z_{2}} Q_{\nu_{1},0}^{U} \textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in A\}} \\[5pt] +\ &\textbf{I}_{\{U_{2} \leq k\}} \textbf{I}_{\{Z_{\nu_{1}} = 0\} } Q_{\nu_{1},s}^{U} \Big(P_{\nu_{1}+1,t_{1}}^{U}\Big)^{s_{1}} \Big(P_{\nu_{1}+1,t_{2}}^{U}\Big)^{s_{2}} Q_{\nu_{1}+1,0}^{U} \textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in B\}} \textbf{I}_{\{\Pi_{\nu_{1}+1}^{U} \in A\}}.\end{align*}
Using that the
![]() $\Pi_{n}^{U}$
are i.i.d. and taking the expectation
$\Pi_{n}^{U}$
are i.i.d. and taking the expectation
![]() $\mathbb{E}_{\delta_{i}^{U}}[\!\cdot\!]$
as in (10), we obtain that
$\mathbb{E}_{\delta_{i}^{U}}[\!\cdot\!]$
as in (10), we obtain that
 \begin{equation*} p_{ik}^{U} \geq \mathbb{P}(U_{1} \leq k) \sum_{z=0}^{L_{U}} H_{k}(z) \mathbb{P}_{\delta_{i}^{U}}(Z_{\nu_{1}}=z),\end{equation*}
\begin{equation*} p_{ik}^{U} \geq \mathbb{P}(U_{1} \leq k) \sum_{z=0}^{L_{U}} H_{k}(z) \mathbb{P}_{\delta_{i}^{U}}(Z_{\nu_{1}}=z),\end{equation*}
where
![]() $H_{k}\;:\; S^{L} \to \mathbb{R}$
is given by
$H_{k}\;:\; S^{L} \to \mathbb{R}$
is given by
 \begin{equation*} H_{k}(z) = \begin{cases} \mathbb{E}\Big[Q_{\nu_{1},s}^{U} \Big(P_{\nu_{1}+1,t_{1}}^{U}\Big)^{s_{1}} \Big(P_{\nu_{1}+1,t_{2}}^{U}\Big)^{s_{2}} Q_{\nu_{1}+1,0}^{U} \textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in B\}} \textbf{I}_{\{\Pi_{\nu_{1}+1}^{U} \in A\}}\Big] & \text{ if } z = 0, \\[5pt] \mathbb{E}\Big[\Big(P_{\nu_{1},k_{1}}^{U}\Big)^{z_{1}} \Big(P_{\nu_{1},k_{2}}^{U}\Big)^{z_{2}} Q_{\nu_{1},0}^{U} \textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in A\}}\Big] & \text{ if } z \neq 0.\end{cases}\end{equation*}
\begin{equation*} H_{k}(z) = \begin{cases} \mathbb{E}\Big[Q_{\nu_{1},s}^{U} \Big(P_{\nu_{1}+1,t_{1}}^{U}\Big)^{s_{1}} \Big(P_{\nu_{1}+1,t_{2}}^{U}\Big)^{s_{2}} Q_{\nu_{1}+1,0}^{U} \textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in B\}} \textbf{I}_{\{\Pi_{\nu_{1}+1}^{U} \in A\}}\Big] & \text{ if } z = 0, \\[5pt] \mathbb{E}\Big[\Big(P_{\nu_{1},k_{1}}^{U}\Big)^{z_{1}} \Big(P_{\nu_{1},k_{2}}^{U}\Big)^{z_{2}} Q_{\nu_{1},0}^{U} \textbf{I}_{\{\Pi_{\nu_{1}}^{U} \in A\}}\Big] & \text{ if } z \neq 0.\end{cases}\end{equation*}
Since
![]() $\sum_{z=0}^{L_{U}} \mathbb{P}_{\delta_{i}^{U}}\big(Z_{\nu_{1}}=z\big) = 1$
, we conclude that
$\sum_{z=0}^{L_{U}} \mathbb{P}_{\delta_{i}^{U}}\big(Z_{\nu_{1}}=z\big) = 1$
, we conclude that
![]() $p_{ik}^{U} \geq \underline{p}_{k}^{U}$
, where
$p_{ik}^{U} \geq \underline{p}_{k}^{U}$
, where
This concludes the proof of (ii). If, instead of 2, 3 holds, the proof is similar: one notices that for all
![]() $z \in S^{L}$
, on the event
$z \in S^{L}$
, on the event
![]() $\{U_{1} \leq k\} \cap \{Z_{\nu_{1}}=z\}$
, there is a positive probability that at time
$\{U_{1} \leq k\} \cap \{Z_{\nu_{1}}=z\}$
, there is a positive probability that at time
![]() $\nu_{1}+1$
there are k immigrants and the z individuals have no offspring. A detailed proof can be obtained in the same manner as above.
$\nu_{1}+1$
there are k immigrants and the z individuals have no offspring. A detailed proof can be obtained in the same manner as above.
Before turning to the proof of Theorem 2.3, we introduce some notation. Let
![]() $T_{i,0}^{L} \;:\!=\; 0$
and
$T_{i,0}^{L} \;:\!=\; 0$
and
![]() $T_{i,l}^{L} \;:\!=\; \inf \big\{ j > T_{i,l-1}^{L} \;:\; Z_{\nu_{j}}=i \big\}$
,
$T_{i,l}^{L} \;:\!=\; \inf \big\{ j > T_{i,l-1}^{L} \;:\; Z_{\nu_{j}}=i \big\}$
,
![]() $l \geq 1$
, be the random times at which the Markov chain
$l \geq 1$
, be the random times at which the Markov chain
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
enters state
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
enters state
![]() $i \in S^{L}$
when the initial state is
$i \in S^{L}$
when the initial state is
![]() $Z_{\nu_{0}}=i$
. Similarly, we let
$Z_{\nu_{0}}=i$
. Similarly, we let
![]() $T_{i,0}^{U} \;:\!=\; 1$
and
$T_{i,0}^{U} \;:\!=\; 1$
and
![]() $T_{i,l}^{U} \;:\!=\; \inf \{ j > T_{i,l-1}^{U} \;:\; Z_{\tau_{j}}=i \}$
,
$T_{i,l}^{U} \;:\!=\; \inf \{ j > T_{i,l-1}^{U} \;:\; Z_{\tau_{j}}=i \}$
,
![]() $l \geq 1$
, be the random times at which the Markov chain
$l \geq 1$
, be the random times at which the Markov chain
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
enters state
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
enters state
![]() $i \in S^{U}$
when the initial state is
$i \in S^{U}$
when the initial state is
![]() $Z_{\tau_{1}}=i$
. The expected times of visiting state k starting from i are denoted by
$Z_{\tau_{1}}=i$
. The expected times of visiting state k starting from i are denoted by
![]() $f_{ik}^{L} \;:\!=\; \mathbb{E}_{\delta_{i}^{L}}\big[T_{k,1}^{L}\big]$
and
$f_{ik}^{L} \;:\!=\; \mathbb{E}_{\delta_{i}^{L}}\big[T_{k,1}^{L}\big]$
and
![]() $f_{ik}^{U} \;:\!=\; \mathbb{E}_{\delta_{i}^{U}}\big[T_{k,1}^{U}-1\big]$
, respectively.
$f_{ik}^{U} \;:\!=\; \mathbb{E}_{\delta_{i}^{U}}\big[T_{k,1}^{U}-1\big]$
, respectively.
Proof of Theorem
2.3. Lemma 3.1 implies that the state spaces of
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
are
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
are
![]() $S^{L}$
and
$S^{L}$
and
![]() $S^{U}$
, respectively. Next, to establish ergodicity of these Markov chains, it is sufficient to verify irreducibility, aperiodicity, and positive recurrence. Irreducibility and aperiodicity follow from Lemma 3.1 in both cases. Now, turning to positive recurrence, let
$S^{U}$
, respectively. Next, to establish ergodicity of these Markov chains, it is sufficient to verify irreducibility, aperiodicity, and positive recurrence. Irreducibility and aperiodicity follow from Lemma 3.1 in both cases. Now, turning to positive recurrence, let
![]() $I_{n}^{L}(k) \;:\!=\; \{ (i_{1},i_{2}, \dots, i_{n-1}) \;:\; i_{j} \in S^{L} \setminus \{ k \} \}$
for
$I_{n}^{L}(k) \;:\!=\; \{ (i_{1},i_{2}, \dots, i_{n-1}) \;:\; i_{j} \in S^{L} \setminus \{ k \} \}$
for
![]() $k \in S^{L}$
. Then, using the Markov property and Part (i) of Lemma 3.1, it follows that
$k \in S^{L}$
. Then, using the Markov property and Part (i) of Lemma 3.1, it follows that
 \begin{align*} f_{kk}^{L} &=\sum_{n=1}^{\infty} \mathbb{P}_{\delta_{k}^{L}}\big(T_{k,1}^{L} \geq n\big) =\sum_{n=1}^{\infty} \mathbb{P}_{\delta_{k}^{L}}\Big(\!\cap_{j=1}^{n-1} \big\{Z_{\nu_{j}} \neq k\big\}\Big) \\[5pt] &=\sum_{n=1}^{\infty} p_{k i_{1}} \prod_{I_{n}^{L}(k)} p_{i_{j-1}i_{j}} \leq \sum_{n=1}^{\infty} \Big(1-\underline{p}^{L}\Big)^{n-1} < \infty.\end{align*}
\begin{align*} f_{kk}^{L} &=\sum_{n=1}^{\infty} \mathbb{P}_{\delta_{k}^{L}}\big(T_{k,1}^{L} \geq n\big) =\sum_{n=1}^{\infty} \mathbb{P}_{\delta_{k}^{L}}\Big(\!\cap_{j=1}^{n-1} \big\{Z_{\nu_{j}} \neq k\big\}\Big) \\[5pt] &=\sum_{n=1}^{\infty} p_{k i_{1}} \prod_{I_{n}^{L}(k)} p_{i_{j-1}i_{j}} \leq \sum_{n=1}^{\infty} \Big(1-\underline{p}^{L}\Big)^{n-1} < \infty.\end{align*}
Now from the finiteness of
![]() $S^{L}$
it follows that
$S^{L}$
it follows that
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
is uniformly ergodic. Next, as above, for all
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
is uniformly ergodic. Next, as above, for all
![]() $k \in S^{U}$
,
$k \in S^{U}$
,
To complete the proof of uniform ergodicity of
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
, we will verify the Doeblin condition for one-step transition: that is, for a probability distribution
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
, we will verify the Doeblin condition for one-step transition: that is, for a probability distribution
![]() $q=\{ q_{k} \}_{k \in S^{U}}$
and every set
$q=\{ q_{k} \}_{k \in S^{U}}$
and every set
![]() $A \subset S^{U}$
satisfying
$A \subset S^{U}$
satisfying
![]() $\sum_{k \in A} q_{k} > \epsilon$
,
$\sum_{k \in A} q_{k} > \epsilon$
,
 \begin{equation*} \inf_{l \in S^{U}} \Bigg( \sum_{k \in A} p_{lk}^{U}\Bigg) > \delta.\end{equation*}
\begin{equation*} \inf_{l \in S^{U}} \Bigg( \sum_{k \in A} p_{lk}^{U}\Bigg) > \delta.\end{equation*}
Now, taking
![]() $q_{k} \;:\!=\; \big(\underline{p}_{k}^{U}\big)/\big(\sum_{k \in S} \underline{p}_{k}^{U}\big)$
, it follows from Lemma 3.1(ii) that
$q_{k} \;:\!=\; \big(\underline{p}_{k}^{U}\big)/\big(\sum_{k \in S} \underline{p}_{k}^{U}\big)$
, it follows from Lemma 3.1(ii) that
 \begin{equation*} \inf_{l \in S^{U}} \Bigg( \sum_{k \in A} p_{lk}^{U} \Bigg) \geq \Bigg(\sum_{k \in S} \underline{p}_{k}^{U}\Bigg) \sum_{k \in A} q_{k}.\end{equation*}
\begin{equation*} \inf_{l \in S^{U}} \Bigg( \sum_{k \in A} p_{lk}^{U} \Bigg) \geq \Bigg(\sum_{k \in S} \underline{p}_{k}^{U}\Bigg) \sum_{k \in A} q_{k}.\end{equation*}
Choosing
![]() $\delta=(\sum_{k \in S} \underline{p}_{k}^{U}) \epsilon$
yields uniform ergodicity of
$\delta=(\sum_{k \in S} \underline{p}_{k}^{U}) \epsilon$
yields uniform ergodicity of
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
.
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
.
Remark 3.1. An immediate consequence of the above theorem is that
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
possesses a proper stationary distribution
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
possesses a proper stationary distribution
![]() $\pi^{L}=\big\{ \pi_{k}^{L} \big\}_{k \in S^{L}}$
, where
$\pi^{L}=\big\{ \pi_{k}^{L} \big\}_{k \in S^{L}}$
, where
![]() $\pi_{k}^{L} \;:\!=\; 1/f_{kk}^{L}>0$
and satisfies
$\pi_{k}^{L} \;:\!=\; 1/f_{kk}^{L}>0$
and satisfies
![]() $\pi_{k}^{L}=\sum_{i \in S} \pi_{i}^{L} p_{ik}^{L}$
for all
$\pi_{k}^{L}=\sum_{i \in S} \pi_{i}^{L} p_{ik}^{L}$
for all
![]() $k \in S^{L}$
. Furthermore,
$k \in S^{L}$
. Furthermore,
![]() $\lim_{j \to \infty} \sup_{l \in S^{L}} \lVert p_{l}^{L}(j)- \pi^{L}\rVert = 0$
, where
$\lim_{j \to \infty} \sup_{l \in S^{L}} \lVert p_{l}^{L}(j)- \pi^{L}\rVert = 0$
, where
![]() $\lVert\cdot\rVert$
denotes the total variation norm. Furthermore, under a finite-second-moment hypothesis, the central limit theorem holds for functions of
$\lVert\cdot\rVert$
denotes the total variation norm. Furthermore, under a finite-second-moment hypothesis, the central limit theorem holds for functions of
![]() $Z_{\nu_{j}}$
. A similar comment also holds for
$Z_{\nu_{j}}$
. A similar comment also holds for
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
with L replaced by U.
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
with L replaced by U.
Remark 3.2. It is worth noticing that the stationary distributions
![]() $\pi^{L}$
and
$\pi^{L}$
and
![]() $\pi^{U}$
are connected using
$\pi^{U}$
are connected using
![]() $\pi_{i}^{L}=\sum_{l \in S^{U}} \mathbb{P}_{\delta_{l}^{U}}\big(Z_{\nu_{1}}=i\big) \pi_{l}^{U}$
for all
$\pi_{i}^{L}=\sum_{l \in S^{U}} \mathbb{P}_{\delta_{l}^{U}}\big(Z_{\nu_{1}}=i\big) \pi_{l}^{U}$
for all
![]() $i \in S^{L}$
, since by time-homogeneity (Lemma A.1) we have
$i \in S^{L}$
, since by time-homogeneity (Lemma A.1) we have
![]() $\mathbb{P}\big(Z_{\nu_{j+1}}=i | Z_{\tau_{j+1}}=l\big)=\mathbb{P}_{\delta_{l}^{U}}\big(Z_{\nu_{1}}=i\big)$
. Now, if we take the limit as
$\mathbb{P}\big(Z_{\nu_{j+1}}=i | Z_{\tau_{j+1}}=l\big)=\mathbb{P}_{\delta_{l}^{U}}\big(Z_{\nu_{1}}=i\big)$
. Now, if we take the limit as
![]() $j \to \infty$
in
$j \to \infty$
in
the above expression follows. Similarly,
![]() $\pi_{k}^{U}=\sum_{l \in S^{L}} \mathbb{P}_{\delta_{l}^{L}}\big(Z_{\tau_{1}}=k\big) \pi_{l}^{L}$
for all
$\pi_{k}^{U}=\sum_{l \in S^{L}} \mathbb{P}_{\delta_{l}^{L}}\big(Z_{\tau_{1}}=k\big) \pi_{l}^{L}$
for all
![]() $k \in S^{U}$
.
$k \in S^{U}$
.
Since the state space
![]() $S^{L}$
is finite,
$S^{L}$
is finite,
![]() $\pi^{L}$
has moments of all orders. Proposition A.1 in Appendix A.3 shows that
$\pi^{L}$
has moments of all orders. Proposition A.1 in Appendix A.3 shows that
![]() $\pi^{U}$
has a finite first moment
$\pi^{U}$
has a finite first moment
![]() $\overline{\pi}^{U} \;:\!=\; \sum_{k \in S^{U}} k \pi_{k}^{U}$
.
$\overline{\pi}^{U} \;:\!=\; \sum_{k \in S^{U}} k \pi_{k}^{U}$
.
4. Regenerative property of crossing times
In this section, we establish the law of large numbers and central limit theorem for the lengths of the supercritical and subcritical regimes
![]() $\big\{ \Delta_{j}^{U} \big\}_{j=1}^{\infty}$
and
$\big\{ \Delta_{j}^{U} \big\}_{j=1}^{\infty}$
and
![]() $\big\{ \Delta_{j}^{L} \big\}_{j=1}^{\infty}$
. To this end, we will show that
$\big\{ \Delta_{j}^{L} \big\}_{j=1}^{\infty}$
. To this end, we will show that
![]() $\big\{ \Delta_{j}^{U} \big\}_{j=1}^{\infty}$
and
$\big\{ \Delta_{j}^{U} \big\}_{j=1}^{\infty}$
and
![]() $\big\{ \Delta_{j}^{L} \big\}_{j=1}^{\infty}$
are regenerative over the times
$\big\{ \Delta_{j}^{L} \big\}_{j=1}^{\infty}$
are regenerative over the times
![]() $\big\{ T_{i,l}^{L} \big\}_{l=0}^{\infty}$
and
$\big\{ T_{i,l}^{L} \big\}_{l=0}^{\infty}$
and
![]() $\big\{ T_{i,l}^{U} \big\}_{l=1}^{\infty}$
, respectively. In our analysis we will also encounter the random variables
$\big\{ T_{i,l}^{U} \big\}_{l=1}^{\infty}$
, respectively. In our analysis we will also encounter the random variables
![]() $\overline{\Delta}_{j}^{U} \;:\!=\; \Delta_{j}^{U}+\Delta_{j}^{L}$
and
$\overline{\Delta}_{j}^{U} \;:\!=\; \Delta_{j}^{U}+\Delta_{j}^{L}$
and
![]() $\overline{\Delta}_{j}^{L} \;:\!=\; \Delta_{j}^{L}+\Delta_{j+1}^{U}$
. For
$\overline{\Delta}_{j}^{L} \;:\!=\; \Delta_{j}^{L}+\Delta_{j+1}^{U}$
. For
![]() $l \geq 1$
and
$l \geq 1$
and
![]() $i \in S^{L}$
, let
$i \in S^{L}$
, let
![]() $B_{i,l}^{L} \;:\!=\; \Big(K_{i,l}^{L}, \boldsymbol{\Delta}_{i,l}^{L}, \overline{\boldsymbol{\Delta}}_{i,l}^{L}\Big)$
, where
$B_{i,l}^{L} \;:\!=\; \Big(K_{i,l}^{L}, \boldsymbol{\Delta}_{i,l}^{L}, \overline{\boldsymbol{\Delta}}_{i,l}^{L}\Big)$
, where
The triple
![]() $B_{i,l}^{L}$
consists of the random time
$B_{i,l}^{L}$
consists of the random time
![]() $K_{i,l}^{L}$
required for
$K_{i,l}^{L}$
required for
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
to return for the lth time to state i, the lengths of all supercritical regimes
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
to return for the lth time to state i, the lengths of all supercritical regimes
![]() $\Delta_{j}^{U}$
between the
$\Delta_{j}^{U}$
between the
![]() $(l-1)$
th return and the lth return, and the lengths
$(l-1)$
th return and the lth return, and the lengths
![]() $\overline{\Delta}_{j}^{U}$
of both regimes in the same time interval. Similarly, for
$\overline{\Delta}_{j}^{U}$
of both regimes in the same time interval. Similarly, for
![]() $l \geq 1$
and
$l \geq 1$
and
![]() $i \in S^{U}$
we let
$i \in S^{U}$
we let
![]() $B_{i,l}^{U} \;:\!=\; \Big(K_{i,l}^{U}, \boldsymbol{\Delta}_{i,l}^{U}, \overline{\boldsymbol{\Delta}}_{i,l}^{U}\Big)$
, where
$B_{i,l}^{U} \;:\!=\; \Big(K_{i,l}^{U}, \boldsymbol{\Delta}_{i,l}^{U}, \overline{\boldsymbol{\Delta}}_{i,l}^{U}\Big)$
, where
The proof of the following lemma is included in Appendix A.4.
Lemma 4.1.
Assume (
H1
)–(
H4
). (i) If (
H5
)also holds and
![]() $Z_{\nu_{0}}=i \in S^{L}$
, then
$Z_{\nu_{0}}=i \in S^{L}$
, then
![]() $\{ B_{i,l}^{L} \}_{l=1}^{\infty}$
are i.i.d. (ii) (
H6
) (or (
H7
)) holds and
$\{ B_{i,l}^{L} \}_{l=1}^{\infty}$
are i.i.d. (ii) (
H6
) (or (
H7
)) holds and
![]() $Z_{\tau_{1}}=i \in S^{U}$
, then
$Z_{\tau_{1}}=i \in S^{U}$
, then
![]() $\{ B_{i,l}^{U} \}_{l=1}^{\infty}$
are i.i.d.
$\{ B_{i,l}^{U} \}_{l=1}^{\infty}$
are i.i.d.
The proof of the following lemma, which is required in the proof of the Theorem 2.4, is also included in Appendix A.4. We need the following additional notation:
![]() $\overline{S}_{n}^{U} \;:\!=\; \sum_{j=1}^{n} \overline{\Delta}_{j}^{U}$
,
$\overline{S}_{n}^{U} \;:\!=\; \sum_{j=1}^{n} \overline{\Delta}_{j}^{U}$
,
![]() $\overline{S}_{n}^{L} \;:\!=\; \sum_{j=1}^{n} \overline{\Delta}_{j}^{L}$
,
$\overline{S}_{n}^{L} \;:\!=\; \sum_{j=1}^{n} \overline{\Delta}_{j}^{L}$
,
 \begin{align*} &\overline{\sigma}^{2,U} \;:\!=\; \mathbb{V}_{\pi^{L}}\Big[\overline{\Delta}_{1}^{U}\Big] + 2\sum_{j=1}^{\infty} \mathbb{C}_{\pi^{L}}\Big[\overline{\Delta}_{1}^{U}, \overline{\Delta}_{j+1}^{U}\Big], \\[5pt] &\overline{\sigma}^{2,L} \;:\!=\; \mathbb{V}_{\pi^{U}}\Big[\overline{\Delta}_{1}^{L}\Big] +2 \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{U}}\Big[\overline{\Delta}_{1}^{L}, \overline{\Delta}_{j+1}^{L}\Big], \\[5pt] &\mathbb{C}^{U} \;:\!=\; \sum_{j=0}^{\infty} \mathbb{C}_{\pi^{L}}\Big[ \Delta_{1}^{U}, \overline{\Delta}_{j+1}^{U}\Big] + \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{L}}\Big[ \overline{\Delta}_{1}^{U}, \Delta_{j+1}^{U}\Big],\quad \text{ and} \\[5pt] &\mathbb{C}^{L} \;:\!=\; \sum_{j=0}^{\infty} \mathbb{C}_{\pi^{U}}\Big[\Delta_{1}^{L}, \overline{\Delta}_{j+1}^{L}\Big] + \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{U}}\Big[\overline{\Delta}_{1}^{L}, \Delta_{j+1}^{L}\Big].\end{align*}
\begin{align*} &\overline{\sigma}^{2,U} \;:\!=\; \mathbb{V}_{\pi^{L}}\Big[\overline{\Delta}_{1}^{U}\Big] + 2\sum_{j=1}^{\infty} \mathbb{C}_{\pi^{L}}\Big[\overline{\Delta}_{1}^{U}, \overline{\Delta}_{j+1}^{U}\Big], \\[5pt] &\overline{\sigma}^{2,L} \;:\!=\; \mathbb{V}_{\pi^{U}}\Big[\overline{\Delta}_{1}^{L}\Big] +2 \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{U}}\Big[\overline{\Delta}_{1}^{L}, \overline{\Delta}_{j+1}^{L}\Big], \\[5pt] &\mathbb{C}^{U} \;:\!=\; \sum_{j=0}^{\infty} \mathbb{C}_{\pi^{L}}\Big[ \Delta_{1}^{U}, \overline{\Delta}_{j+1}^{U}\Big] + \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{L}}\Big[ \overline{\Delta}_{1}^{U}, \Delta_{j+1}^{U}\Big],\quad \text{ and} \\[5pt] &\mathbb{C}^{L} \;:\!=\; \sum_{j=0}^{\infty} \mathbb{C}_{\pi^{U}}\Big[\Delta_{1}^{L}, \overline{\Delta}_{j+1}^{L}\Big] + \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{U}}\Big[\overline{\Delta}_{1}^{L}, \Delta_{j+1}^{L}\Big].\end{align*}
Lemma 4.2.
Under the assumptions of Theorem 2.4, for all
![]() $i \in S^{L}$
the following hold:
$i \in S^{L}$
the following hold:
 \begin{align*} &\text{(i) } \mathbb{E}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U}\Big] = \big(\pi_{i}^{L}\big)^{-1} \mu^{U} \quad \text{ and } \quad\mathbb{E}_{\delta_{i}^{L}}\Big[\overline{S}_{T_{i,1}^{L}}^{U}\Big] = \big(\pi_{i}^{L}\big)^{-1} \big(\mu^{U}+\mu^{L}\big); \\[5pt] &\text{(ii) } \mathbb{V}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U}\Big] = \big(\pi_{i}^{L}\big)^{-1} \sigma^{2,U} \quad \text{ and } \quad\mathbb{V}_{\delta_{i}^{L}}\Big[\overline{S}_{T_{i,1}^{L}}^{U}\Big] = \big(\pi_{i}^{L}\big)^{-1} \overline{\sigma}^{2,U}; \quad \text{ and} \\[5pt] &\text{(iii) } \mathbb{C}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U},\overline{S}_{T_{i,1}^{L}}^{U}\Big] = \big(\pi_{i}^{L}\big)^{-1} \mathbb{C}^{U}.\end{align*}
\begin{align*} &\text{(i) } \mathbb{E}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U}\Big] = \big(\pi_{i}^{L}\big)^{-1} \mu^{U} \quad \text{ and } \quad\mathbb{E}_{\delta_{i}^{L}}\Big[\overline{S}_{T_{i,1}^{L}}^{U}\Big] = \big(\pi_{i}^{L}\big)^{-1} \big(\mu^{U}+\mu^{L}\big); \\[5pt] &\text{(ii) } \mathbb{V}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U}\Big] = \big(\pi_{i}^{L}\big)^{-1} \sigma^{2,U} \quad \text{ and } \quad\mathbb{V}_{\delta_{i}^{L}}\Big[\overline{S}_{T_{i,1}^{L}}^{U}\Big] = \big(\pi_{i}^{L}\big)^{-1} \overline{\sigma}^{2,U}; \quad \text{ and} \\[5pt] &\text{(iii) } \mathbb{C}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U},\overline{S}_{T_{i,1}^{L}}^{U}\Big] = \big(\pi_{i}^{L}\big)^{-1} \mathbb{C}^{U}.\end{align*}
The above statements also hold with U replaced by L.
Proposition A.2 in Appendix A.5 shows that
![]() $\sigma^{2,T}$
and
$\sigma^{2,T}$
and
![]() $\overline{\sigma}^{2,T}$
are positive and finite, and
$\overline{\sigma}^{2,T}$
are positive and finite, and
![]() $\lvert\mathbb{C}^{T}\rvert<\infty$
. We are now ready to prove Theorem 2.4. The proof relies on decomposing
$\lvert\mathbb{C}^{T}\rvert<\infty$
. We are now ready to prove Theorem 2.4. The proof relies on decomposing
![]() $S_{n}^{U}$
and
$S_{n}^{U}$
and
![]() $S_{n}^{L}$
into i.i.d. cycles using Lemma 4.1. Specifically, conditionally on
$S_{n}^{L}$
into i.i.d. cycles using Lemma 4.1. Specifically, conditionally on
![]() $Z_{\nu_{0}}=i \in S^{L}$
(resp.
$Z_{\nu_{0}}=i \in S^{L}$
(resp.
![]() $Z_{\tau_{1}}=i \in S^{U}$
), the random variables
$Z_{\tau_{1}}=i \in S^{U}$
), the random variables
![]() $\Big\{ S_{T_{i,l}^{L}}^{U}-S_{T_{i,l-1}^{L}}^{U} \Big\}_{l=1}^{\infty}$
$\Big\{ S_{T_{i,l}^{L}}^{U}-S_{T_{i,l-1}^{L}}^{U} \Big\}_{l=1}^{\infty}$
![]() $\Big(\textrm{resp.}\;\Big\{ S_{T_{i,l}^{U}-1}^{L}-S_{T_{i,l-1}^{U}-1}^{L} \Big\}_{l=1}^{\infty}\Big)$
are i.i.d.
$\Big(\textrm{resp.}\;\Big\{ S_{T_{i,l}^{U}-1}^{L}-S_{T_{i,l-1}^{U}-1}^{L} \Big\}_{l=1}^{\infty}\Big)$
are i.i.d.
Proof of Theorem
2.4. We begin by proving (i). For
![]() $i \in S^{L}$
and
$i \in S^{L}$
and
![]() $n \in \mathbb{N}$
, let
$n \in \mathbb{N}$
, let
be the number of times
![]() $T_{i,l}^{L}$
is in
$T_{i,l}^{L}$
is in
![]() $\{ 0,1,\dots,n \}$
. Conditionally on
$\{ 0,1,\dots,n \}$
. Conditionally on
![]() $Z_{\nu_{0}}=i$
, notice that
$Z_{\nu_{0}}=i$
, notice that
![]() $N_{i}^{L}(n)$
is a renewal process (recall that
$N_{i}^{L}(n)$
is a renewal process (recall that
![]() $T_{i,0}^{L}=0$
). We recall that
$T_{i,0}^{L}=0$
). We recall that
![]() $K_{i,l}^{L} = T_{i,l}^{L}-T_{i,l-1}^{L}$
and let
$K_{i,l}^{L} = T_{i,l}^{L}-T_{i,l-1}^{L}$
and let
Using the decomposition
 \begin{equation} \frac{1}{n} S_{n}^{U} = \frac{N_{i}^{L}(n)}{n} \Bigg( \frac{1}{N_{i}^{L}(n)} \sum_{l=1}^{N_{i}^{L}(n)} R_{i,l}^{L} + \frac{1}{N_{i}^{L}(n)} R_{i,n}^{*,L} \Bigg)\end{equation}
\begin{equation} \frac{1}{n} S_{n}^{U} = \frac{N_{i}^{L}(n)}{n} \Bigg( \frac{1}{N_{i}^{L}(n)} \sum_{l=1}^{N_{i}^{L}(n)} R_{i,l}^{L} + \frac{1}{N_{i}^{L}(n)} R_{i,n}^{*,L} \Bigg)\end{equation}
and the fact that
![]() $\big\{ R_{i,l}^{L} \big\}_{l=1}^{\infty}$
are i.i.d. and
$\big\{ R_{i,l}^{L} \big\}_{l=1}^{\infty}$
are i.i.d. and
![]() $\lim_{n \to \infty} N_{i}^{L}(n) = \infty$
a.s., we obtain using the law of large numbers for random sums and Lemma 4.2(i) that
$\lim_{n \to \infty} N_{i}^{L}(n) = \infty$
a.s., we obtain using the law of large numbers for random sums and Lemma 4.2(i) that
 \begin{equation} \lim_{n \to \infty} \frac{1}{N_{i}^{L}(n)} \sum_{l=1}^{N_{i}^{L}(n)} R_{i,l}^{L} = \mathbb{E}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U}\Big]=(\pi_{i}^{L})^{-1} \mu^{U} \text{ a.s.}\end{equation}
\begin{equation} \lim_{n \to \infty} \frac{1}{N_{i}^{L}(n)} \sum_{l=1}^{N_{i}^{L}(n)} R_{i,l}^{L} = \mathbb{E}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U}\Big]=(\pi_{i}^{L})^{-1} \mu^{U} \text{ a.s.}\end{equation}
Also,
Finally, using the key renewal theorem (Corollary 2.11 of Serfozo [Reference Serfozo27]) and Remark 3.1, we have
Using (15) and (16) in (14), we obtain the strong law of large numbers for
![]() $S_{n}^{U}$
. Turning to the central limit theorem, we let
$S_{n}^{U}$
. Turning to the central limit theorem, we let
![]() $\underline{R}_{i,l}^{L} \;:\!=\; R_{i,l}^{L} - \mu^{U} K_{i,l}^{L}$
and
$\underline{R}_{i,l}^{L} \;:\!=\; R_{i,l}^{L} - \mu^{U} K_{i,l}^{L}$
and
![]() $\underline{R}_{i,n}^{*,L} \;:\!=\; R_{i,n}^{*,L} - \mu^{U} K_{i,n}^{*,L}$
. Conditionally on
$\underline{R}_{i,n}^{*,L} \;:\!=\; R_{i,n}^{*,L} - \mu^{U} K_{i,n}^{*,L}$
. Conditionally on
![]() $Z_{\nu_{0}}=i$
, using the decomposition in (14) and centering, we obtain
$Z_{\nu_{0}}=i$
, using the decomposition in (14) and centering, we obtain
 \begin{equation*} \frac{1}{\sqrt{n}}\big(S_{n}^{U}-n\mu^{U}\big) = \sqrt{\frac{N_{i}^{L}(n)}{n}} \left( \frac{1}{\sqrt{N_{i}^{L}(n)}} \sum_{l=1}^{N_{i}^{L}(n)} \underline{R}_{i,l}^{L} + \frac{1}{\sqrt{N_{i}^{L}(n)}} \underline{R}_{i,n}^{*,L} \right),\end{equation*}
\begin{equation*} \frac{1}{\sqrt{n}}\big(S_{n}^{U}-n\mu^{U}\big) = \sqrt{\frac{N_{i}^{L}(n)}{n}} \left( \frac{1}{\sqrt{N_{i}^{L}(n)}} \sum_{l=1}^{N_{i}^{L}(n)} \underline{R}_{i,l}^{L} + \frac{1}{\sqrt{N_{i}^{L}(n)}} \underline{R}_{i,n}^{*,L} \right),\end{equation*}
where
![]() $\big\{ \underline{R}_{i,l}^{L} \big\}_{l=1}^{\infty}$
are i.i.d. with mean 0 and variance
$\big\{ \underline{R}_{i,l}^{L} \big\}_{l=1}^{\infty}$
are i.i.d. with mean 0 and variance
by Lemma 4.2. Finally, using the central limit theorem for i.i.d. random sums and (16), it follows that
 \begin{equation*} \sqrt{\frac{N_{i}^{L}(n)}{n}} \left( \frac{1}{\sqrt{N_{i}^{L}(n)}} \sum_{l=1}^{N_{i}^{L}(n)} \underline{R}_{i,l}^{L} \right) \xrightarrow[n \to \infty]{d} N\big(0,\sigma^{2,U}\big).\end{equation*}
\begin{equation*} \sqrt{\frac{N_{i}^{L}(n)}{n}} \left( \frac{1}{\sqrt{N_{i}^{L}(n)}} \sum_{l=1}^{N_{i}^{L}(n)} \underline{R}_{i,l}^{L} \right) \xrightarrow[n \to \infty]{d} N\big(0,\sigma^{2,U}\big).\end{equation*}
To complete the proof notice that
 \begin{equation*} \lvert \frac{1}{\sqrt{N_{i}^{L}(n)}} \underline{R}_{i,n}^{*,L}\rvert \leq \frac{1}{\sqrt{N_{i}^{L}(n)}} \lvert\underline{R}_{i,N_{i}^{L}(n)+1}^{L}\rvert \xrightarrow[n \to \infty]{p} 0.\end{equation*}
\begin{equation*} \lvert \frac{1}{\sqrt{N_{i}^{L}(n)}} \underline{R}_{i,n}^{*,L}\rvert \leq \frac{1}{\sqrt{N_{i}^{L}(n)}} \lvert\underline{R}_{i,N_{i}^{L}(n)+1}^{L}\rvert \xrightarrow[n \to \infty]{p} 0.\end{equation*}
The proof for
![]() $S_{n}^{L}$
is similar.
$S_{n}^{L}$
is similar.
When studying the proportion of time the process spends in the supercritical and subcritical regimes, we will need the above theorem with n replaced by a random time
![]() $\tilde{N}(n)$
.
$\tilde{N}(n)$
.
Remark 4.1. Theorem 2.4 holds if n is replaced by a random time
![]() $\tilde{N}(n)$
, where
$\tilde{N}(n)$
, where
![]() $\lim_{n \to \infty} \tilde{N}(n)=\infty$
a.s.
$\lim_{n \to \infty} \tilde{N}(n)=\infty$
a.s.
5. Proportion of time spent in supercritical and subcritical regimes
We recall that
![]() $\chi_{n}^U =\textbf{I}_{\cup_{j=1}^{\infty} [\nu_{j-1},\tau_{j})}(n)$
is 1 if the process is in the supercritical regime and 0 otherwise, and similarly
$\chi_{n}^U =\textbf{I}_{\cup_{j=1}^{\infty} [\nu_{j-1},\tau_{j})}(n)$
is 1 if the process is in the supercritical regime and 0 otherwise, and similarly
![]() $\chi_{n}^L=1-\chi_{n}^U$
. Also,
$\chi_{n}^L=1-\chi_{n}^U$
. Also,
![]() $\theta_{n}^{U}=\frac{1}{n} C_{n}^U$
is the proportion of time the process spends in the supercritical regime up to time
$\theta_{n}^{U}=\frac{1}{n} C_{n}^U$
is the proportion of time the process spends in the supercritical regime up to time
![]() $n-1$
; the quantity
$n-1$
; the quantity
![]() $\theta_{n}^{L}$
is defined similarly. The limit theorems for
$\theta_{n}^{L}$
is defined similarly. The limit theorems for
![]() $\theta_{n}^{U}$
and
$\theta_{n}^{U}$
and
![]() $\theta_{n}^{L}$
will invoke the i.i.d. blocks developed in Section 4. Let
$\theta_{n}^{L}$
will invoke the i.i.d. blocks developed in Section 4. Let
![]() $\boldsymbol{S}_{n}^{U} \;:\!=\; \big(S_{n}^{U}, \overline{S}_{n}^{U}\big)^{\top}$
,
$\boldsymbol{S}_{n}^{U} \;:\!=\; \big(S_{n}^{U}, \overline{S}_{n}^{U}\big)^{\top}$
,
![]() $\boldsymbol{\mu}^{U} \;:\!=\; \big(\mu^{U},\mu^{U}+\mu^{L}\big)^{\top}$
,
$\boldsymbol{\mu}^{U} \;:\!=\; \big(\mu^{U},\mu^{U}+\mu^{L}\big)^{\top}$
,
![]() $\boldsymbol{\mu}^{L} \;:\!=\; \big(\mu^{L},\mu^{U}+\mu^{L}\big)^{\top}$
, and
$\boldsymbol{\mu}^{L} \;:\!=\; \big(\mu^{L},\mu^{U}+\mu^{L}\big)^{\top}$
, and
 \begin{equation*} \Sigma^{U} \;:\!=\; \begin{pmatrix} \sigma^{2,U} & \mathbb{C}^{U} \\[5pt] \mathbb{C}^{U} & \overline{\sigma}^{2,U} \end{pmatrix}, \qquad \Sigma^{L} \;:\!=\; \begin{pmatrix} \sigma^{2,L} & \mathbb{C}^{L} \\[5pt] \mathbb{C}^{L} & \overline{\sigma}^{2,L} \end{pmatrix}.\end{equation*}
\begin{equation*} \Sigma^{U} \;:\!=\; \begin{pmatrix} \sigma^{2,U} & \mathbb{C}^{U} \\[5pt] \mathbb{C}^{U} & \overline{\sigma}^{2,U} \end{pmatrix}, \qquad \Sigma^{L} \;:\!=\; \begin{pmatrix} \sigma^{2,L} & \mathbb{C}^{L} \\[5pt] \mathbb{C}^{L} & \overline{\sigma}^{2,L} \end{pmatrix}.\end{equation*}
We note that while
![]() $S_{n}^{U}$
represents the length of the first n supercritical regimes,
$S_{n}^{U}$
represents the length of the first n supercritical regimes,
![]() $\overline{S}_{n}^{U}$
is the total time taken for the process to complete the first n cycles.
$\overline{S}_{n}^{U}$
is the total time taken for the process to complete the first n cycles.
Lemma 5.1.
Under the conditions of Theorem 2.5,
![]() $\frac{1}{\sqrt{n}} \big(\boldsymbol{S}_{n}^{U}-n\boldsymbol{\mu}^{U}\big) \xrightarrow[n \to \infty]{d} N\big(\textbf{0},\Sigma^{U}\big)$
, and
$\frac{1}{\sqrt{n}} \big(\boldsymbol{S}_{n}^{U}-n\boldsymbol{\mu}^{U}\big) \xrightarrow[n \to \infty]{d} N\big(\textbf{0},\Sigma^{U}\big)$
, and
![]() $\frac{1}{\sqrt{n}} \big(\boldsymbol{S}_{n}^{L}-n\boldsymbol{\mu}^{L}\big) \xrightarrow[n \to \infty]{d} N\big(\textbf{0},\Sigma^{L}\big)$
.
$\frac{1}{\sqrt{n}} \big(\boldsymbol{S}_{n}^{L}-n\boldsymbol{\mu}^{L}\big) \xrightarrow[n \to \infty]{d} N\big(\textbf{0},\Sigma^{L}\big)$
.
Proof of Lemma 5.1. The proof is similar to that of Theorem 2.4. We let
 \begin{align*} \boldsymbol{R}_{i,l}^{L} &\;:\!=\; \boldsymbol{S}_{T_{i,l}^{L}}^{U}-\boldsymbol{S}_{T_{i,l-1}^{L}}^{U}, \qquad \boldsymbol{R}_{i,n}^{*,L} \;:\!=\; \boldsymbol{S}_{n}^{U}-\boldsymbol{S}_{T_{i,N_{i}^{L}(n)}^{L}}^{U}, \\[5pt] \underline{\boldsymbol{R}}_{i,l}^{L} &\;:\!=\; \boldsymbol{R}_{i,l}^{L} - K_{i,l}^{L} \boldsymbol{\mu}^{U}, \qquad \underline{\boldsymbol{R}}_{i,n}^{*,L} \;:\!=\; \boldsymbol{R}_{i,n}^{*,L} - K_{i,n}^{*,L} \boldsymbol{\mu}^{U}. \end{align*}
\begin{align*} \boldsymbol{R}_{i,l}^{L} &\;:\!=\; \boldsymbol{S}_{T_{i,l}^{L}}^{U}-\boldsymbol{S}_{T_{i,l-1}^{L}}^{U}, \qquad \boldsymbol{R}_{i,n}^{*,L} \;:\!=\; \boldsymbol{S}_{n}^{U}-\boldsymbol{S}_{T_{i,N_{i}^{L}(n)}^{L}}^{U}, \\[5pt] \underline{\boldsymbol{R}}_{i,l}^{L} &\;:\!=\; \boldsymbol{R}_{i,l}^{L} - K_{i,l}^{L} \boldsymbol{\mu}^{U}, \qquad \underline{\boldsymbol{R}}_{i,n}^{*,L} \;:\!=\; \boldsymbol{R}_{i,n}^{*,L} - K_{i,n}^{*,L} \boldsymbol{\mu}^{U}. \end{align*}
Conditionally on
![]() $Z_{\nu_{0}}=i$
, we write
$Z_{\nu_{0}}=i$
, we write
 \begin{equation*} \frac{1}{\sqrt{n}} \big(\boldsymbol{S}_{n}^{U}-n\boldsymbol{\mu}^{U}\big) = \sqrt{\frac{N_{i}^{L}(n)}{n}} \left( \frac{1}{\sqrt{N_{i}^{L}(n)}} \sum_{l=1}^{N_{i}^{L}(n)} \underline{\boldsymbol{R}}_{i,l}^{L} + \frac{1}{\sqrt{N_{i}^{L}(n)}} \underline{\boldsymbol{R}}_{i,n}^{*,L} \right).\end{equation*}
\begin{equation*} \frac{1}{\sqrt{n}} \big(\boldsymbol{S}_{n}^{U}-n\boldsymbol{\mu}^{U}\big) = \sqrt{\frac{N_{i}^{L}(n)}{n}} \left( \frac{1}{\sqrt{N_{i}^{L}(n)}} \sum_{l=1}^{N_{i}^{L}(n)} \underline{\boldsymbol{R}}_{i,l}^{L} + \frac{1}{\sqrt{N_{i}^{L}(n)}} \underline{\boldsymbol{R}}_{i,n}^{*,L} \right).\end{equation*}
Now, by Lemma 4.1 and Lemma 4.2,
![]() $\big\{ \underline{\boldsymbol{R}}_{i,l}^{L} \big\}_{l=1}^{\infty}$
are i.i.d. with mean
$\big\{ \underline{\boldsymbol{R}}_{i,l}^{L} \big\}_{l=1}^{\infty}$
are i.i.d. with mean
![]() $\textbf{0}=(0,0)^{\top}$
and covariance matrix
$\textbf{0}=(0,0)^{\top}$
and covariance matrix
![]() $(\pi_{i}^{L})^{-1} \Sigma^{U}$
. Using the key renewal theorem, we conclude that
$(\pi_{i}^{L})^{-1} \Sigma^{U}$
. Using the key renewal theorem, we conclude that
 \begin{equation*} \sqrt{\frac{N_{i}^{L}(n)}{n}} \left( \frac{1}{\sqrt{N_{i}^{L}(n)}} \sum_{l=1}^{N_{i}^{L}(n)} \underline{\boldsymbol{R}}_{i,l}^{L} \right) \xrightarrow[n \to \infty]{d} N\big(\textbf{0},\Sigma^{U}\big)\end{equation*}
\begin{equation*} \sqrt{\frac{N_{i}^{L}(n)}{n}} \left( \frac{1}{\sqrt{N_{i}^{L}(n)}} \sum_{l=1}^{N_{i}^{L}(n)} \underline{\boldsymbol{R}}_{i,l}^{L} \right) \xrightarrow[n \to \infty]{d} N\big(\textbf{0},\Sigma^{U}\big)\end{equation*}
and
 \begin{equation*} \frac{1}{\sqrt{N_{i}^{L}(n)}} \lvert\underline{\boldsymbol{R}}_{i,n}^{*,L}\rvert \xrightarrow[n \to \infty]{p} 0.\end{equation*}
\begin{equation*} \frac{1}{\sqrt{N_{i}^{L}(n)}} \lvert\underline{\boldsymbol{R}}_{i,n}^{*,L}\rvert \xrightarrow[n \to \infty]{p} 0.\end{equation*}
The proof of (ii) is similar.
Remark 5.1. Lemma 5.1 also holds with n replaced by a random time
![]() $\tilde{N}(n)$
such that
$\tilde{N}(n)$
such that
![]() $\lim_{n \to \infty} \tilde{N}(n)=\infty$
a.s. The next lemma concerns the number of crossings of upper and lower thresholds, namely,
$\lim_{n \to \infty} \tilde{N}(n)=\infty$
a.s. The next lemma concerns the number of crossings of upper and lower thresholds, namely,
![]() $\tilde{N}^{U}(n) \;:\!=\; \sup \{ j \geq 0 \;:\; \tau_{j} \leq n \}$
and
$\tilde{N}^{U}(n) \;:\!=\; \sup \{ j \geq 0 \;:\; \tau_{j} \leq n \}$
and
![]() $\tilde{N}^{L}(n) \;:\!=\; \sup \{ j \geq 0 \;:\; \nu_{j} \leq n \}$
, where
$\tilde{N}^{L}(n) \;:\!=\; \sup \{ j \geq 0 \;:\; \nu_{j} \leq n \}$
, where
![]() $n \in \mathbb{N}_{0}$
.
$n \in \mathbb{N}_{0}$
.
Lemma 5.2. Under the conditions of Theorem 2.5,
-
(i)
 $\lim_{n \to \infty} \frac{\tilde{N}^{U}(n)}{n+1} = \frac{1}{\mu^{U}+\mu^{L}}$
and
$\lim_{n \to \infty} \frac{\tilde{N}^{U}(n)}{n+1} = \frac{1}{\mu^{U}+\mu^{L}}$
and
 $\lim_{n \to \infty} \frac{\tilde{N}^{L}(n)}{n+1} = \frac{1}{\mu^{U}+\mu^{L}}$
a.s.;
$\lim_{n \to \infty} \frac{\tilde{N}^{L}(n)}{n+1} = \frac{1}{\mu^{U}+\mu^{L}}$
a.s.;
-
(ii)
 $\lim_{n \to \infty} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} = \mu^{U}$
and
$\lim_{n \to \infty} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} = \mu^{U}$
and
 $\lim_{n \to \infty} \frac{C_{n+1}^{L}}{\tilde{N}^{L}(n)} = \mu^{L}$
a.s.
$\lim_{n \to \infty} \frac{C_{n+1}^{L}}{\tilde{N}^{L}(n)} = \mu^{L}$
a.s.
Proof of Lemma
5.2. We begin by proving (i). We recall that
![]() $\tau_{0}=-1$
and
$\tau_{0}=-1$
and
![]() $\tau_{j} < \nu_{j} < \tau_{j+1}$
a.s. for all
$\tau_{j} < \nu_{j} < \tau_{j+1}$
a.s. for all
![]() $j \geq 0$
, yielding that
$j \geq 0$
, yielding that
Since
![]() $\tau_{j}$
and
$\tau_{j}$
and
![]() $\nu_{j}$
are finite a.s., we obtain that
$\nu_{j}$
are finite a.s., we obtain that
![]() $\lim_{n \to \infty} \tilde{N}^{U}(n)=\infty$
and
$\lim_{n \to \infty} \tilde{N}^{U}(n)=\infty$
and
![]() $\lim_{n \to \infty} \tilde{N}^{L}(n)=\infty$
a.s. Part (i) follows if we show that
$\lim_{n \to \infty} \tilde{N}^{L}(n)=\infty$
a.s. Part (i) follows if we show that
To this end, we notice that
![]() $\nu_{\tilde{N}^{L}(n)} \leq n \leq \nu_{\tilde{N}^{L}(n)+1}$
, and for
$\nu_{\tilde{N}^{L}(n)} \leq n \leq \nu_{\tilde{N}^{L}(n)+1}$
, and for
![]() $n \geq \nu_{1}$
,
$n \geq \nu_{1}$
,
Clearly,
![]() $\lim_{n \to \infty} \frac{\tilde{N}^{L}(n)+1}{\tilde{N}^{L}(n)} = 1$
a.s. By Remark 4.1 with
$\lim_{n \to \infty} \frac{\tilde{N}^{L}(n)+1}{\tilde{N}^{L}(n)} = 1$
a.s. By Remark 4.1 with
![]() $\tilde{N}(n)=\tilde{N}^{U}(n)$
,
$\tilde{N}(n)=\tilde{N}^{U}(n)$
,
 \begin{equation*} \lim_{n \to \infty} \frac{\nu_{\tilde{N}^{L}(n)}}{\tilde{N}^{L}(n)}=\lim_{n \to \infty} \frac{1}{\tilde{N}^{L}(n)} \sum_{j=1}^{\tilde{N}^{L}(n)} \overline{\Delta}_{j}^{U} = \mu^{U}+\mu^{L} \text{ a.s.}\end{equation*}
\begin{equation*} \lim_{n \to \infty} \frac{\nu_{\tilde{N}^{L}(n)}}{\tilde{N}^{L}(n)}=\lim_{n \to \infty} \frac{1}{\tilde{N}^{L}(n)} \sum_{j=1}^{\tilde{N}^{L}(n)} \overline{\Delta}_{j}^{U} = \mu^{U}+\mu^{L} \text{ a.s.}\end{equation*}
Thus, we obtain
Turning to (ii), we notice that
 \begin{equation*} C_{n+1}^{U} = \sum_{j=0}^{n} \chi_{j}^{U} = \sum_{j=1}^{\tilde{N}^{U}(n)} \Delta_{j}^{U}+\sum_{l=\nu_{\tilde{N}^{U}(n)}}^{n} 1,\end{equation*}
\begin{equation*} C_{n+1}^{U} = \sum_{j=0}^{n} \chi_{j}^{U} = \sum_{j=1}^{\tilde{N}^{U}(n)} \Delta_{j}^{U}+\sum_{l=\nu_{\tilde{N}^{U}(n)}}^{n} 1,\end{equation*}
where
![]() $\sum_{l=r}^{n}=0$
for
$\sum_{l=r}^{n}=0$
for
![]() $r>n$
. Remark 4.1 with
$r>n$
. Remark 4.1 with
![]() $\tilde{N}(n)=\tilde{N}^{U}(n)$
yields that
$\tilde{N}(n)=\tilde{N}^{U}(n)$
yields that
 \begin{align*} &\lim_{n \to \infty} \frac{1}{\tilde{N}^{U}(n)} \sum_{j=1}^{\tilde{N}^{U}(n)} \Delta_{j}^{U} = \mu^{U} \text{ a.s. and } \\[5pt] &\limsup_{n \to \infty} \frac{1}{\tilde{N}^{U}(n)} \sum_{l=\nu_{\tilde{N}^{U}(n)}}^{n} 1 \leq \lim_{n \to \infty} \frac{1}{\tilde{N}^{U}(n)} \Delta_{\tilde{N}^{U}(n)+1}^{U} = 0 \text{ a.s.}\end{align*}
\begin{align*} &\lim_{n \to \infty} \frac{1}{\tilde{N}^{U}(n)} \sum_{j=1}^{\tilde{N}^{U}(n)} \Delta_{j}^{U} = \mu^{U} \text{ a.s. and } \\[5pt] &\limsup_{n \to \infty} \frac{1}{\tilde{N}^{U}(n)} \sum_{l=\nu_{\tilde{N}^{U}(n)}}^{n} 1 \leq \lim_{n \to \infty} \frac{1}{\tilde{N}^{U}(n)} \Delta_{\tilde{N}^{U}(n)+1}^{U} = 0 \text{ a.s.}\end{align*}
Thus, we obtain that
![]() $\lim_{n \to \infty} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} = \mu^{U}$
a.s. Similarly,
$\lim_{n \to \infty} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} = \mu^{U}$
a.s. Similarly,
![]() $\lim_{n \to \infty} \frac{C_{n+1}^{L}}{\tilde{N}^{L}(n)} = \mu^{L}$
a.s.
$\lim_{n \to \infty} \frac{C_{n+1}^{L}}{\tilde{N}^{L}(n)} = \mu^{L}$
a.s.
Our next result is concerned with the joint distribution of the last time when the process is in a specific regime and the proportion of time the process spends in that regime, under the assumptions of Theorem 2.5. Let
 \begin{equation*} \overline{\Sigma}^{U} \;:\!=\; \begin{pmatrix} \sigma^{2,U}\big(\mu^{U}+\mu^{L}\big)\;\;\;\;\;\; & -\frac{\mathbb{C}^{U}}{\mu^{U}+\mu^{L}} \\[5pt] -\frac{\mathbb{C}^{U}}{\mu^{U}+\mu^{L}}\;\;\;\;\;\; & \frac{\overline{\sigma}^{2,U}}{\big(\mu^{U}+\mu^{L}\big)^{3}} \end{pmatrix} \quad \text{ and } \quad \overline{\Sigma}^{L} \;:\!=\; \begin{pmatrix} \sigma^{2,L}\big(\mu^{U}+\mu^{L}\big)\;\;\;\;\;\; & -\frac{\mathbb{C}^{L}}{\mu^{U}+\mu^{L}} \\[5pt] -\frac{\mathbb{C}^{L}}{\mu^{U}+\mu^{L}}\;\;\;\;\;\; & \frac{\overline{\sigma}^{2,L}}{\big(\mu^{U}+\mu^{L}\big)^{3}} \end{pmatrix}.\end{equation*}
\begin{equation*} \overline{\Sigma}^{U} \;:\!=\; \begin{pmatrix} \sigma^{2,U}\big(\mu^{U}+\mu^{L}\big)\;\;\;\;\;\; & -\frac{\mathbb{C}^{U}}{\mu^{U}+\mu^{L}} \\[5pt] -\frac{\mathbb{C}^{U}}{\mu^{U}+\mu^{L}}\;\;\;\;\;\; & \frac{\overline{\sigma}^{2,U}}{\big(\mu^{U}+\mu^{L}\big)^{3}} \end{pmatrix} \quad \text{ and } \quad \overline{\Sigma}^{L} \;:\!=\; \begin{pmatrix} \sigma^{2,L}\big(\mu^{U}+\mu^{L}\big)\;\;\;\;\;\; & -\frac{\mathbb{C}^{L}}{\mu^{U}+\mu^{L}} \\[5pt] -\frac{\mathbb{C}^{L}}{\mu^{U}+\mu^{L}}\;\;\;\;\;\; & \frac{\overline{\sigma}^{2,L}}{\big(\mu^{U}+\mu^{L}\big)^{3}} \end{pmatrix}.\end{equation*}
Lemma 5.3. Under the conditions of Theorem 2.5,
 \begin{align*}\sqrt{n+1}\begin{pmatrix} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} - \mu^{U} \\[5pt] \frac{\tilde{N}^{U}(n)}{n+1}-\frac{1}{\mu^{U}+\mu^{L}}\end{pmatrix} &\xrightarrow[n \to \infty]{d} N\Big(\textbf{0},\overline{\Sigma}^{U}\Big) \quad \text{ and } \quad\\[5pt] \sqrt{n+1}\begin{pmatrix} \frac{C_{n+1}^{L}}{\tilde{N}^{L}(n)} - \mu^{L} \\[5pt] \frac{\tilde{N}^{L}(n)}{n+1}-\frac{1}{\mu^{U}+\mu^{L}}\end{pmatrix} &\xrightarrow[n \to \infty]{d} N\Big(\textbf{0},\overline{\Sigma}^{L}\Big).\end{align*}
\begin{align*}\sqrt{n+1}\begin{pmatrix} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} - \mu^{U} \\[5pt] \frac{\tilde{N}^{U}(n)}{n+1}-\frac{1}{\mu^{U}+\mu^{L}}\end{pmatrix} &\xrightarrow[n \to \infty]{d} N\Big(\textbf{0},\overline{\Sigma}^{U}\Big) \quad \text{ and } \quad\\[5pt] \sqrt{n+1}\begin{pmatrix} \frac{C_{n+1}^{L}}{\tilde{N}^{L}(n)} - \mu^{L} \\[5pt] \frac{\tilde{N}^{L}(n)}{n+1}-\frac{1}{\mu^{U}+\mu^{L}}\end{pmatrix} &\xrightarrow[n \to \infty]{d} N\Big(\textbf{0},\overline{\Sigma}^{L}\Big).\end{align*}
Proof of Lemma
5.3. We only prove the statement for
![]() $C_{n+1}^{U}$
and
$C_{n+1}^{U}$
and
![]() $\tilde{N}^{U}(n)$
, since the other case is similar. We write
$\tilde{N}^{U}(n)$
, since the other case is similar. We write
 \begin{align*}&\sqrt{\tilde{N}^{U}(n)}\begin{pmatrix} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} - \mu^{U} \\[5pt] \frac{n+1}{\tilde{N}^{U}(n)}-\big(\mu^{U}+\mu^{L}\big)\end{pmatrix} \\[5pt] =\ &\frac{1}{\sqrt{\tilde{N}^{U}(n)}} \sum_{j=1}^{\tilde{N}^{U}(n)}\begin{pmatrix} \Delta_{j}^{U}-\mu^{U} \\[5pt] \overline{\Delta}_{j}^{U}-\big(\mu^{U}+\mu^{L}\big)\end{pmatrix} + \frac{1}{\sqrt{\tilde{N}^{U}(n)}} \sum_{l=\nu_{\tilde{N}^{U}(n)}}^{n} \begin{pmatrix} 1 \\[5pt] 1 \end{pmatrix},\end{align*}
\begin{align*}&\sqrt{\tilde{N}^{U}(n)}\begin{pmatrix} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} - \mu^{U} \\[5pt] \frac{n+1}{\tilde{N}^{U}(n)}-\big(\mu^{U}+\mu^{L}\big)\end{pmatrix} \\[5pt] =\ &\frac{1}{\sqrt{\tilde{N}^{U}(n)}} \sum_{j=1}^{\tilde{N}^{U}(n)}\begin{pmatrix} \Delta_{j}^{U}-\mu^{U} \\[5pt] \overline{\Delta}_{j}^{U}-\big(\mu^{U}+\mu^{L}\big)\end{pmatrix} + \frac{1}{\sqrt{\tilde{N}^{U}(n)}} \sum_{l=\nu_{\tilde{N}^{U}(n)}}^{n} \begin{pmatrix} 1 \\[5pt] 1 \end{pmatrix},\end{align*}
and using Lemma 5.1 and Remark 5.1 with
![]() $\tilde{N}(n)=\tilde{N}^{U}(n)$
, we obtain that
$\tilde{N}(n)=\tilde{N}^{U}(n)$
, we obtain that
 \begin{equation*}\sqrt{\tilde{N}^{U}(n)}\begin{pmatrix} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} - \mu^{U} \\[5pt] \frac{n+1}{\tilde{N}^{U}(n)}-\big(\mu^{U}+\mu^{L}\big)\end{pmatrix} \xrightarrow[n \to \infty]{d} N\big(\textbf{0},\Sigma^{U}\big).\end{equation*}
\begin{equation*}\sqrt{\tilde{N}^{U}(n)}\begin{pmatrix} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} - \mu^{U} \\[5pt] \frac{n+1}{\tilde{N}^{U}(n)}-\big(\mu^{U}+\mu^{L}\big)\end{pmatrix} \xrightarrow[n \to \infty]{d} N\big(\textbf{0},\Sigma^{U}\big).\end{equation*}
Next, we apply the delta method with
![]() $g:\mathbb{R}^{2} \to \mathbb{R}^{2}$
given by
$g:\mathbb{R}^{2} \to \mathbb{R}^{2}$
given by
![]() $g(x,y)=(x,1/y)$
and obtain that
$g(x,y)=(x,1/y)$
and obtain that
 \begin{equation*}\sqrt{\tilde{N}^{U}(n)}\begin{pmatrix} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} - \mu^{U} \\[5pt] \frac{\tilde{N}^{U}(n)}{n+1}-\frac{1}{\mu^{U}+\mu^{L}}\end{pmatrix} \xrightarrow[n \to \infty]{d} N\big(\textbf{0},\Sigma_{2}^{U}\big),\end{equation*}
\begin{equation*}\sqrt{\tilde{N}^{U}(n)}\begin{pmatrix} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} - \mu^{U} \\[5pt] \frac{\tilde{N}^{U}(n)}{n+1}-\frac{1}{\mu^{U}+\mu^{L}}\end{pmatrix} \xrightarrow[n \to \infty]{d} N\big(\textbf{0},\Sigma_{2}^{U}\big),\end{equation*}
where
 \begin{equation*} \Sigma_{2}^{U}=J_{g}\big(\boldsymbol{\mu}^{U}\big) \Sigma^{U} J_{g}\big(\boldsymbol{\mu}^{U}\big)^{\top} =\begin{pmatrix} \sigma^{2,U} & -\frac{\mathbb{C}^{U}}{\big(\mu^{U}+\mu^{L}\big)^{2}} \\[5pt] -\frac{\mathbb{C}^{U}}{\big(\mu^{U}+\mu^{L}\big)^{2}} & \frac{\overline{\sigma}^{2,U}}{\big(\mu^{U}+\mu^{L}\big)^{4}} \end{pmatrix}\end{equation*}
\begin{equation*} \Sigma_{2}^{U}=J_{g}\big(\boldsymbol{\mu}^{U}\big) \Sigma^{U} J_{g}\big(\boldsymbol{\mu}^{U}\big)^{\top} =\begin{pmatrix} \sigma^{2,U} & -\frac{\mathbb{C}^{U}}{\big(\mu^{U}+\mu^{L}\big)^{2}} \\[5pt] -\frac{\mathbb{C}^{U}}{\big(\mu^{U}+\mu^{L}\big)^{2}} & \frac{\overline{\sigma}^{2,U}}{\big(\mu^{U}+\mu^{L}\big)^{4}} \end{pmatrix}\end{equation*}
and
![]() $J_{g}(\!\cdot\!)$
is the Jacobian matrix of
$J_{g}(\!\cdot\!)$
is the Jacobian matrix of
![]() $g(\!\cdot\!)$
. Using Lemma 5.2(i), we obtain that
$g(\!\cdot\!)$
. Using Lemma 5.2(i), we obtain that
 \begin{equation*}\sqrt{n+1}\begin{pmatrix} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} - \mu^{U} \\[5pt] \frac{\tilde{N}^{U}(n)}{n+1}-\frac{1}{\mu^{U}+\mu^{L}}\end{pmatrix} \xrightarrow[n \to \infty]{d} N\Big(\textbf{0},\overline{\Sigma}^{U}\Big).\end{equation*}
\begin{equation*}\sqrt{n+1}\begin{pmatrix} \frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)} - \mu^{U} \\[5pt] \frac{\tilde{N}^{U}(n)}{n+1}-\frac{1}{\mu^{U}+\mu^{L}}\end{pmatrix} \xrightarrow[n \to \infty]{d} N\Big(\textbf{0},\overline{\Sigma}^{U}\Big).\end{equation*}
We are now ready to prove Theorem 2.5. Recall that
![]() $\theta_{n}^{U} = \frac{C_{n}^{U}}{n}$
,
$\theta_{n}^{U} = \frac{C_{n}^{U}}{n}$
,
![]() $\theta_{n}^{L} = \frac{C_{n}^{L}}{n}$
,
$\theta_{n}^{L} = \frac{C_{n}^{L}}{n}$
,
![]() $\theta^{U} = \frac{\mu^{U}}{\mu^{U}+\mu^{L}}$
, and
$\theta^{U} = \frac{\mu^{U}}{\mu^{U}+\mu^{L}}$
, and
![]() $\theta^{L} = \frac{\mu^{L}}{\mu^{L}+\mu^{U}}$
, and let
$\theta^{L} = \frac{\mu^{L}}{\mu^{L}+\mu^{U}}$
, and let
![]() $\theta^{k,U}$
and
$\theta^{k,U}$
and
![]() $\theta^{k,L}$
be the kth powers of
$\theta^{k,L}$
be the kth powers of
![]() $\theta^{U}$
and
$\theta^{U}$
and
![]() $\theta^{L}$
, respectively.
$\theta^{L}$
, respectively.
Proof of Theorem
2.5. Almost sure convergence of
![]() $\theta_{n}^{T}$
follows from Lemma 5.3 upon noticing that
$\theta_{n}^{T}$
follows from Lemma 5.3 upon noticing that
 \begin{align*}\frac{C_{n+1}^{T}}{n+1}= \left(\frac{C_{n+1}^{T}}{\tilde{N}^{T}(n)} \right) \left( \frac{\tilde{N}^{T}(n)}{n+1}\right).\end{align*}
\begin{align*}\frac{C_{n+1}^{T}}{n+1}= \left(\frac{C_{n+1}^{T}}{\tilde{N}^{T}(n)} \right) \left( \frac{\tilde{N}^{T}(n)}{n+1}\right).\end{align*}
Using Lemma 5.2 and the decomposition
 \begin{align*} &\sqrt{n+1} \biggl( \frac{C_{n+1}^{T}}{n+1} - \frac{\mu^{T}}{\mu^{U}+\mu^{L}} \biggr) \\[5pt] = &\frac{\tilde{N}^{T}(n)}{n+1} \cdot \sqrt{n+1} \biggl(\frac{C_{n+1}^{T}}{\tilde{N}^{T}(n)} - \mu^{T} \biggr) + \mu^{T} \cdot \sqrt{n+1} \biggl(\frac{\tilde{N}^{T}(n)}{n+1}-\frac{1}{\mu^{U}+\mu^{L}} \biggr),\end{align*}
\begin{align*} &\sqrt{n+1} \biggl( \frac{C_{n+1}^{T}}{n+1} - \frac{\mu^{T}}{\mu^{U}+\mu^{L}} \biggr) \\[5pt] = &\frac{\tilde{N}^{T}(n)}{n+1} \cdot \sqrt{n+1} \biggl(\frac{C_{n+1}^{T}}{\tilde{N}^{T}(n)} - \mu^{T} \biggr) + \mu^{T} \cdot \sqrt{n+1} \biggl(\frac{\tilde{N}^{T}(n)}{n+1}-\frac{1}{\mu^{U}+\mu^{L}} \biggr),\end{align*}
it follows that
![]() $\sqrt{n+1} \big(\theta_{n+1}^{T} - \theta^{T} \big)$
is asymptotically normal with mean zero and variance
$\sqrt{n+1} \big(\theta_{n+1}^{T} - \theta^{T} \big)$
is asymptotically normal with mean zero and variance
Corollary 5.1.
Under the conditions of Theorem 2.4, for
![]() $T \in \{L,U\}$
,
$T \in \{L,U\}$
,
 \begin{equation*} \sqrt{\tilde{N}^{T}(n)} \Bigg(\frac{C_{n+1}^{T}}{\tilde{N}^{T}(n)}- \mu^{T} \Bigg) \xrightarrow[n \to \infty]{d} N\big(0,\sigma^{2,T}\big).\end{equation*}
\begin{equation*} \sqrt{\tilde{N}^{T}(n)} \Bigg(\frac{C_{n+1}^{T}}{\tilde{N}^{T}(n)}- \mu^{T} \Bigg) \xrightarrow[n \to \infty]{d} N\big(0,\sigma^{2,T}\big).\end{equation*}
Proof of Corollary
5.1. We only prove the case
![]() $T=U$
. We write
$T=U$
. We write
 \begin{equation*} \sqrt{\tilde{N}^{U}(n)} \biggl(\frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)}- \mu^{U}\biggr) = \frac{1}{\sqrt{\tilde{N}^{U}(n)}} \sum_{j=1}^{\tilde{N}^{U}(n)} \big(\Delta_{j}^{U} - \mu^{U}\big) + \frac{1}{\sqrt{\tilde{N}^{U}(n)}} \sum_{l=\nu_{\tilde{N}^{U}(n)}}^{n} 1.\end{equation*}
\begin{equation*} \sqrt{\tilde{N}^{U}(n)} \biggl(\frac{C_{n+1}^{U}}{\tilde{N}^{U}(n)}- \mu^{U}\biggr) = \frac{1}{\sqrt{\tilde{N}^{U}(n)}} \sum_{j=1}^{\tilde{N}^{U}(n)} \big(\Delta_{j}^{U} - \mu^{U}\big) + \frac{1}{\sqrt{\tilde{N}^{U}(n)}} \sum_{l=\nu_{\tilde{N}^{U}(n)}}^{n} 1.\end{equation*}
Taking the limit in the above equation and using Remark 4.1 yields the result.
6. Estimating the mean of the offspring distribution
We recall that
![]() $\tilde{\chi}_{n}^{U} = \chi_{n}^{U} \textbf{I}_{\{Z_{n} \geq 1\}}$
,
$\tilde{\chi}_{n}^{U} = \chi_{n}^{U} \textbf{I}_{\{Z_{n} \geq 1\}}$
,
![]() $\tilde{C}_{n}^{U} = \sum_{j=1}^{n} \tilde{\chi}_{j-1}^{U}$
, and for the subcritical regime we set
$\tilde{C}_{n}^{U} = \sum_{j=1}^{n} \tilde{\chi}_{j-1}^{U}$
, and for the subcritical regime we set
![]() $\tilde{\chi}_{n}^{L} \;:\!=\; \chi_{n}^{L}$
and
$\tilde{\chi}_{n}^{L} \;:\!=\; \chi_{n}^{L}$
and
![]() $\tilde{C}_{n}^{L} \;:\!=\; C_{n}^{L}$
. We also recall that the offspring mean estimates of the BPRET
$\tilde{C}_{n}^{L} \;:\!=\; C_{n}^{L}$
. We also recall that the offspring mean estimates of the BPRET
![]() $\{Z_{n} \}_{n=0}^{\infty}$
in the supercritical and subcritical regimes are given by
$\{Z_{n} \}_{n=0}^{\infty}$
in the supercritical and subcritical regimes are given by
 \begin{equation*} M_{n}^{U} = \frac{1}{\tilde{C}_{n}^{U}} \sum_{j=1}^n \frac{Z_{j}-I_{j-1}^{U}}{Z_{j-1}} \tilde{\chi}_{j-1}^U \quad \text{ and } \quad M_{n}^L = \frac{1}{\tilde{C}_{n}^{L}} \sum_{j=1}^n \frac{Z_{j}}{Z_{j-1}} \tilde{\chi}_{j-1}^L.\end{equation*}
\begin{equation*} M_{n}^{U} = \frac{1}{\tilde{C}_{n}^{U}} \sum_{j=1}^n \frac{Z_{j}-I_{j-1}^{U}}{Z_{j-1}} \tilde{\chi}_{j-1}^U \quad \text{ and } \quad M_{n}^L = \frac{1}{\tilde{C}_{n}^{L}} \sum_{j=1}^n \frac{Z_{j}}{Z_{j-1}} \tilde{\chi}_{j-1}^L.\end{equation*}
The decomposition
will be used in the proof of Theorem 2.6 and involves the martingale structure of
![]() $M_{n,i}^{T} \;:\!=\; \sum_{j=1}^{n} D_{j,i}^{T}$
, where
$M_{n,i}^{T} \;:\!=\; \sum_{j=1}^{n} D_{j,i}^{T}$
, where
 \begin{equation} D_{j,1}^{T} \;:\!=\; \Big(\overline{P}_{j-1}^{T}-M^{T}\Big) \tilde{\chi}_{j-1}^T \quad \text{ and } \quad D_{j,2}^{T} \;:\!=\; \frac{\tilde{\chi}_{j-1}^{T}}{Z_{j-1}} \sum_{i=1}^{Z_{j-1}} \Big(\xi_{j-1,i}^{T} - \overline{P}_{j-1}^{T}\Big).\end{equation}
\begin{equation} D_{j,1}^{T} \;:\!=\; \Big(\overline{P}_{j-1}^{T}-M^{T}\Big) \tilde{\chi}_{j-1}^T \quad \text{ and } \quad D_{j,2}^{T} \;:\!=\; \frac{\tilde{\chi}_{j-1}^{T}}{Z_{j-1}} \sum_{i=1}^{Z_{j-1}} \Big(\xi_{j-1,i}^{T} - \overline{P}_{j-1}^{T}\Big).\end{equation}
Specifically, let
![]() $\mathcal{G}_{n}$
be the
$\mathcal{G}_{n}$
be the
![]() $\sigma$
-algebra generated by the random environments
$\sigma$
-algebra generated by the random environments
![]() $\big\{ \Pi_{j}^{T} \big\}_{j=0}^{n}$
;
$\big\{ \Pi_{j}^{T} \big\}_{j=0}^{n}$
;
![]() $\mathcal{H}_{n,1}$
the
$\mathcal{H}_{n,1}$
the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $\mathcal{F}_{n}$
and
$\mathcal{F}_{n}$
and
![]() $\mathcal{G}_{n-1}$
; and
$\mathcal{G}_{n-1}$
; and
![]() $\mathcal{H}_{n,2}$
the
$\mathcal{H}_{n,2}$
the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $\mathcal{F}_{n}$
,
$\mathcal{F}_{n}$
,
![]() $\mathcal{G}_{n-1}$
, and the offspring distributions
$\mathcal{G}_{n-1}$
, and the offspring distributions
![]() $\{ \xi_{j,i}^{T} \}_{i=0}^{\infty}$
,
$\{ \xi_{j,i}^{T} \}_{i=0}^{\infty}$
,
![]() $j=0,1,\dots,n-1$
. Hence,
$j=0,1,\dots,n-1$
. Hence,
![]() $Z_{n}$
,
$Z_{n}$
,
![]() $\tilde{\chi}_{n}^{T}$
, and
$\tilde{\chi}_{n}^{T}$
, and
![]() $\Pi_{n-1}^{T}$
are
$\Pi_{n-1}^{T}$
are
![]() $\mathcal{H}_{n,1}$
-measurable, whereas
$\mathcal{H}_{n,1}$
-measurable, whereas
![]() $\Pi_{n}^{T}$
is not
$\Pi_{n}^{T}$
is not
![]() $\mathcal{H}_{n,1}$
-measurable. We also denote by
$\mathcal{H}_{n,1}$
-measurable. We also denote by
![]() $\tilde{\mathcal{H}}_{n,1}$
the
$\tilde{\mathcal{H}}_{n,1}$
the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $\mathcal{F}_{n-1}$
and
$\mathcal{F}_{n-1}$
and
![]() $\mathcal{G}_{n-1}$
, and by
$\mathcal{G}_{n-1}$
, and by
![]() $\tilde{\mathcal{H}}_{n,2}$
the
$\tilde{\mathcal{H}}_{n,2}$
the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $\mathcal{F}_{n-1}$
,
$\mathcal{F}_{n-1}$
,
![]() $\mathcal{G}_{n-1}$
, and
$\mathcal{G}_{n-1}$
, and
![]() $\{ \xi_{j,i}^{T} \}_{i=0}^{\infty}$
,
$\{ \xi_{j,i}^{T} \}_{i=0}^{\infty}$
,
![]() $j=0,1,\dots,n-1$
. Hence,
$j=0,1,\dots,n-1$
. Hence,
![]() $Z_{n-1}$
,
$Z_{n-1}$
,
![]() $\tilde{\chi}_{n-1}^{T}$
, and
$\tilde{\chi}_{n-1}^{T}$
, and
![]() $\Pi_{n-1}^{T}$
are all
$\Pi_{n-1}^{T}$
are all
![]() $\tilde{\mathcal{H}}_{n,1}$
-measurable but not
$\tilde{\mathcal{H}}_{n,1}$
-measurable but not
![]() $\tilde{\mathcal{H}}_{n-1,1}$
-measurable. We establish in Proposition A.3 in Appendix A.6 that
$\tilde{\mathcal{H}}_{n-1,1}$
-measurable. We establish in Proposition A.3 in Appendix A.6 that
are mean-zero martingale sequences. Additionally,
where
 \begin{align*}\tilde{A}_{n}^{U} \;:\!=\; \sum_{j=1}^n \frac{\tilde{\chi}_{j-1}^U}{Z_{j-1}}\end{align*}
\begin{align*}\tilde{A}_{n}^{U} \;:\!=\; \sum_{j=1}^n \frac{\tilde{\chi}_{j-1}^U}{Z_{j-1}}\end{align*}
is the sum of
![]() $\frac{1}{Z_{j}}$
over supercritical time steps up to time
$\frac{1}{Z_{j}}$
over supercritical time steps up to time
![]() $n-1$
, discarding times at which
$n-1$
, discarding times at which
![]() $Z_{j}$
is zero, and
$Z_{j}$
is zero, and
 \begin{align*}\tilde{A}_{n}^{L} \;:\!=\; A_{n}^{L} \;:\!=\; \sum_{j=1}^n \frac{\chi_{j-1}^L}{Z_{j-1}}\end{align*}
\begin{align*}\tilde{A}_{n}^{L} \;:\!=\; A_{n}^{L} \;:\!=\; \sum_{j=1}^n \frac{\chi_{j-1}^L}{Z_{j-1}}\end{align*}
is the sum of
![]() $\frac{1}{Z_{j}}$
over subcritical time steps up to time
$\frac{1}{Z_{j}}$
over subcritical time steps up to time
![]() $n-1$
. Proposition A.3 contains other two martingales involving the terms
$n-1$
. Proposition A.3 contains other two martingales involving the terms
![]() $D_{j,1}^{T}$
and
$D_{j,1}^{T}$
and
![]() $D_{j,2}^{T}$
in (21) and related moment bounds, which will be used in the proof of Theorem 2.6. As a first step, we derive the limit of the variances
$D_{j,2}^{T}$
in (21) and related moment bounds, which will be used in the proof of Theorem 2.6. As a first step, we derive the limit of the variances
![]() $\mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big]$
and
$\mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big]$
and
![]() $\mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big]$
when rescaled by n. By Proposition A.3, this entails studying the limit behavior of the quantities
$\mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big]$
when rescaled by n. By Proposition A.3, this entails studying the limit behavior of the quantities
![]() $\frac{1}{n} \tilde{C}_{n}^{T}$
and
$\frac{1}{n} \tilde{C}_{n}^{T}$
and
![]() $\frac{1}{n} \tilde{A}_{n}^{T}$
. To this end, we build i.i.d. blocks as in Section 4. For
$\frac{1}{n} \tilde{A}_{n}^{T}$
. To this end, we build i.i.d. blocks as in Section 4. For
![]() $l \geq 1$
and
$l \geq 1$
and
![]() $i \in S^{L}$
, let
$i \in S^{L}$
, let
![]() $\overline{B}_{i,l}^{L} \;:\!=\; \Big(K_{i,l}^{L}, \tilde{\boldsymbol{\Delta}}_{i,l}^{L}, \tilde{\boldsymbol{\Gamma}}_{i,l}^{L}\Big)$
, where
$\overline{B}_{i,l}^{L} \;:\!=\; \Big(K_{i,l}^{L}, \tilde{\boldsymbol{\Delta}}_{i,l}^{L}, \tilde{\boldsymbol{\Gamma}}_{i,l}^{L}\Big)$
, where
 \begin{align*} K_{i,l}^{L} &= T_{i,l}^{L}-T_{i,l-1}^{L}, \qquad \tilde{\boldsymbol{\Delta}}_{i,l}^{L} \;:\!=\; \Big( \tilde{\Delta}_{T_{i,l-1}^{L}+1}^{U}, \dots, \tilde{\Delta}_{T_{i,l}^{L}}^{U}\Big), \qquad \tilde{\boldsymbol{\Gamma}}_{i,l}^{L} \;:\!=\; \Big( \tilde{\Gamma}_{T_{i,l-1}^{L}+1}^{U}, \dots, \tilde{\Gamma}_{T_{i,l}^{L}}^{U}\Big), \\[5pt] \tilde{\Delta}_{j+1}^{U} &\;:\!=\; \sum_{k=\nu_{j}+1}^{\tau_{j+1}} \tilde{\chi}_{k-1}^{U}, \qquad \tilde{\Gamma}_{j+1}^{U} \;:\!=\; \sum_{k=\nu_{j}+1}^{\tau_{j+1}} \frac{\tilde{\chi}_{k-1}^{U}}{Z_{k-1}}.\end{align*}
\begin{align*} K_{i,l}^{L} &= T_{i,l}^{L}-T_{i,l-1}^{L}, \qquad \tilde{\boldsymbol{\Delta}}_{i,l}^{L} \;:\!=\; \Big( \tilde{\Delta}_{T_{i,l-1}^{L}+1}^{U}, \dots, \tilde{\Delta}_{T_{i,l}^{L}}^{U}\Big), \qquad \tilde{\boldsymbol{\Gamma}}_{i,l}^{L} \;:\!=\; \Big( \tilde{\Gamma}_{T_{i,l-1}^{L}+1}^{U}, \dots, \tilde{\Gamma}_{T_{i,l}^{L}}^{U}\Big), \\[5pt] \tilde{\Delta}_{j+1}^{U} &\;:\!=\; \sum_{k=\nu_{j}+1}^{\tau_{j+1}} \tilde{\chi}_{k-1}^{U}, \qquad \tilde{\Gamma}_{j+1}^{U} \;:\!=\; \sum_{k=\nu_{j}+1}^{\tau_{j+1}} \frac{\tilde{\chi}_{k-1}^{U}}{Z_{k-1}}.\end{align*}
The triple
![]() $B_{i,l}^{L}$
consists of the random time
$B_{i,l}^{L}$
consists of the random time
![]() $K_{i,l}^{L}$
required for
$K_{i,l}^{L}$
required for
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
to return for the lth time to state i, the lengths of all supercritical regimes
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
to return for the lth time to state i, the lengths of all supercritical regimes
![]() $\tilde{\Delta}_{j}^{U}$
between the
$\tilde{\Delta}_{j}^{U}$
between the
![]() $(l-1)$
th return and the lth return, and the sum of
$(l-1)$
th return and the lth return, and the sum of
![]() $Z_{j}$
-inverse over supercritical regimes, disregarding the times when the process hits zero. Similarly, for
$Z_{j}$
-inverse over supercritical regimes, disregarding the times when the process hits zero. Similarly, for
![]() $l \geq 1$
and
$l \geq 1$
and
![]() $i \in S^{U}$
we let
$i \in S^{U}$
we let
![]() $\overline{B}_{i,l}^{U} \;:\!=\; \big(K_{i,l}^{U}, \boldsymbol{\Delta}_{i,l}^{U}, \boldsymbol{\Gamma}_{i,l}^{U}\big)$
, where
$\overline{B}_{i,l}^{U} \;:\!=\; \big(K_{i,l}^{U}, \boldsymbol{\Delta}_{i,l}^{U}, \boldsymbol{\Gamma}_{i,l}^{U}\big)$
, where
 \begin{align*} K_{i,l}^{U} &= T_{i,l}^{U}-T_{i,l-1}^{U}, \qquad \boldsymbol{\Delta}_{i,l}^{U} = \Big( \Delta_{T_{i,l-1}^{U}}^{L}, \dots, \Delta_{T_{i,l}^{U}-1}^{L}\Big), \qquad\boldsymbol{\Gamma}_{i,l}^{U} \;:\!=\; \Big( \Gamma_{T_{i,l-1}^{U}}^{L}, \dots, \Gamma_{T_{i,l}^{U}-1}^{L}\Big), \\[5pt] \Gamma_{j}^{L} &\;:\!=\; \sum_{k=\tau_{j}+1}^{\nu_{j}} \frac{\chi_{k-1}^{L}}{Z_{k-1}}.\end{align*}
\begin{align*} K_{i,l}^{U} &= T_{i,l}^{U}-T_{i,l-1}^{U}, \qquad \boldsymbol{\Delta}_{i,l}^{U} = \Big( \Delta_{T_{i,l-1}^{U}}^{L}, \dots, \Delta_{T_{i,l}^{U}-1}^{L}\Big), \qquad\boldsymbol{\Gamma}_{i,l}^{U} \;:\!=\; \Big( \Gamma_{T_{i,l-1}^{U}}^{L}, \dots, \Gamma_{T_{i,l}^{U}-1}^{L}\Big), \\[5pt] \Gamma_{j}^{L} &\;:\!=\; \sum_{k=\tau_{j}+1}^{\nu_{j}} \frac{\chi_{k-1}^{L}}{Z_{k-1}}.\end{align*}
Notice that, since
![]() $\tilde{C}_{n}^{L}=C_{n}^{L}$
, Theorem 2.5 already yields that
$\tilde{C}_{n}^{L}=C_{n}^{L}$
, Theorem 2.5 already yields that
![]() $\lim_{n \to \infty} \frac{C_{n}^{L}}{n} = \frac{\mu^{L}}{\mu^{U}+\mu^{L}}$
. We need the following slight modification of Lemma 4.1, whose proof is similar and hence omitted.
$\lim_{n \to \infty} \frac{C_{n}^{L}}{n} = \frac{\mu^{L}}{\mu^{U}+\mu^{L}}$
. We need the following slight modification of Lemma 4.1, whose proof is similar and hence omitted.
Lemma 6.1.
Assume (
H1
)–(
H4
). (i) If (
H5
) holds and
![]() $Z_{\nu_{0}}=i \in S^{L}$
, then
$Z_{\nu_{0}}=i \in S^{L}$
, then
![]() $\big\{ \overline{B}_{i,l}^{L} \big\}_{l=1}^{\infty}$
are i.i.d. (
H6
) (or (
H7
)) holds and
$\big\{ \overline{B}_{i,l}^{L} \big\}_{l=1}^{\infty}$
are i.i.d. (
H6
) (or (
H7
)) holds and
![]() $Z_{\tau_{1}}=i \in S^{U}$
, then
$Z_{\tau_{1}}=i \in S^{U}$
, then
![]() $\{ \overline{B}_{i,l}^{U} \}_{l=1}^{\infty}$
are i.i.d.
$\{ \overline{B}_{i,l}^{U} \}_{l=1}^{\infty}$
are i.i.d.
Proposition 6.1.
Suppose that (
H1
)–(
H6
) (or (
H7
)) hold and
![]() $\mu^{U},\mu^{L}<\infty$
. Then
$\mu^{U},\mu^{L}<\infty$
. Then
-
(i)
 $\lim_{n \to \infty} \frac{\tilde{C}_{n}^{U}}{\tilde{N}^{L}(n)} = \tilde{\mu}^{U}$
and
$\lim_{n \to \infty} \frac{\tilde{C}_{n}^{U}}{\tilde{N}^{L}(n)} = \tilde{\mu}^{U}$
and
 $\lim_{n \to \infty} \frac{\tilde{C}_{n}^{U}}{n} = \frac{\tilde{\mu}^{U}}{\mu^{U}+\mu^{L}}$
a.s.;
$\lim_{n \to \infty} \frac{\tilde{C}_{n}^{U}}{n} = \frac{\tilde{\mu}^{U}}{\mu^{U}+\mu^{L}}$
a.s.;
-
(ii)
 $\lim_{n \to \infty} \frac{\tilde{A}_{n}^{U}}{\tilde{N}^{L}(n)} = \tilde{A}^{U}$
and
$\lim_{n \to \infty} \frac{\tilde{A}_{n}^{U}}{\tilde{N}^{L}(n)} = \tilde{A}^{U}$
and
 $\lim_{n \to \infty} \frac{\tilde{A}_{n}^{U}}{n} = \frac{\tilde{A}^{U}}{\mu^{U}+\mu^{L}}$
a.s.;
$\lim_{n \to \infty} \frac{\tilde{A}_{n}^{U}}{n} = \frac{\tilde{A}^{U}}{\mu^{U}+\mu^{L}}$
a.s.;
-
(iii)
 $\lim_{n \to \infty} \frac{A_{n}^{L}}{\tilde{N}^{U}(n)} = A^{L}$
and
$\lim_{n \to \infty} \frac{A_{n}^{L}}{\tilde{N}^{U}(n)} = A^{L}$
and
 $\lim_{n \to \infty} \frac{A_{n}^{L}}{n} = \frac{A^{L}}{\mu^{U}+\mu^{L}}$
a.s.
$\lim_{n \to \infty} \frac{A_{n}^{L}}{n} = \frac{A^{L}}{\mu^{U}+\mu^{L}}$
a.s.
Since
![]() $\frac{\tilde{C}_{n}^{T}}{n}$
and
$\frac{\tilde{C}_{n}^{T}}{n}$
and
![]() $\frac{\tilde{A}_{n}^{T}}{n}$
are non-negative and bounded by one, Proposition 6.1 implies convergence in mean of these quantities.
$\frac{\tilde{A}_{n}^{T}}{n}$
are non-negative and bounded by one, Proposition 6.1 implies convergence in mean of these quantities.
Proof of Proposition
6.1. By Lemma 5.2(i) it is enough to show the first part of the statements (i)–(iii). Since the proofs of the other cases are similar, we only prove (i). We recall that for
![]() $i \in S^{L}$
and
$i \in S^{L}$
and
![]() $j \in \mathbb{N}$
,
$j \in \mathbb{N}$
,
is the number of times
![]() $T_{i,l}^{L}$
is in
$T_{i,l}^{L}$
is in
![]() $\{ 0,1,\dots,j \}$
. We define
$\{ 0,1,\dots,j \}$
. We define
Conditionally on
![]() $Z_{\nu_{0}}=i$
,
$Z_{\nu_{0}}=i$
,
![]() $T_{i,0}^{L}=0$
, and we write
$T_{i,0}^{L}=0$
, and we write
 \begin{equation*} \frac{\tilde{C}_{n}^{U}}{\tilde{N}^{L}(n)} = \frac{\overline{N}_{i}^{L}(n)}{\tilde{N}^{L}(n)} \left( \frac{1}{\overline{N}_{i}^{L}(n)} \sum_{l=1}^{\overline{N}_{i}^{L}(n)} \tilde{D}_{i,l}^{L} + \frac{1}{\overline{N}_{i}^{L}(n)} \tilde{D}_{i,n}^{*,L} \right).\end{equation*}
\begin{equation*} \frac{\tilde{C}_{n}^{U}}{\tilde{N}^{L}(n)} = \frac{\overline{N}_{i}^{L}(n)}{\tilde{N}^{L}(n)} \left( \frac{1}{\overline{N}_{i}^{L}(n)} \sum_{l=1}^{\overline{N}_{i}^{L}(n)} \tilde{D}_{i,l}^{L} + \frac{1}{\overline{N}_{i}^{L}(n)} \tilde{D}_{i,n}^{*,L} \right).\end{equation*}
Lemma 6.1 implies that
![]() $\big\{ \tilde{D}_{i,l}^{L} \big\}_{l=1}^{\infty}$
are i.i.d. with expectation given by
$\big\{ \tilde{D}_{i,l}^{L} \big\}_{l=1}^{\infty}$
are i.i.d. with expectation given by
using Proposition 1.69 of Serfozo [Reference Serfozo27]. Since
![]() $\lim_{n \to \infty} \overline{N}_{i}^{L}(n) = \infty$
a.s., we obtain that
$\lim_{n \to \infty} \overline{N}_{i}^{L}(n) = \infty$
a.s., we obtain that
 \begin{equation*} \lim_{n \to \infty} \frac{1}{\overline{N}_{i}^{L}(n)} \sum_{l=1}^{\overline{N}_{i}^{L}(n)} \tilde{D}_{i,l}^{L} = (\pi_{i}^{L})^{-1} \tilde{\mu}^{U} \text{ a.s. and } \lim_{n \to \infty} \frac{1}{\overline{N}_{i}^{L}(n)} \tilde{D}_{i,n}^{*,L} =0 \text{ a.s.,}\end{equation*}
\begin{equation*} \lim_{n \to \infty} \frac{1}{\overline{N}_{i}^{L}(n)} \sum_{l=1}^{\overline{N}_{i}^{L}(n)} \tilde{D}_{i,l}^{L} = (\pi_{i}^{L})^{-1} \tilde{\mu}^{U} \text{ a.s. and } \lim_{n \to \infty} \frac{1}{\overline{N}_{i}^{L}(n)} \tilde{D}_{i,n}^{*,L} =0 \text{ a.s.,}\end{equation*}
since
Finally, it holds that
![]() $\lim_{n \to \infty} \frac{\overline{N}_{i}^{L}(n)}{\tilde{N}^{L}(n)} = \pi_{i}^{L}$
a.s.
$\lim_{n \to \infty} \frac{\overline{N}_{i}^{L}(n)}{\tilde{N}^{L}(n)} = \pi_{i}^{L}$
a.s.
We next establish that, when rescaled by their standard deviations, the terms
![]() $M_{n,i}^{T}$
, where
$M_{n,i}^{T}$
, where
![]() $i=1,2$
and
$i=1,2$
and
![]() $T \in \{L,U\}$
, are jointly asymptotically normal. To this end, let
$T \in \{L,U\}$
, are jointly asymptotically normal. To this end, let
 \begin{equation*} \overline{\boldsymbol{M}}_{n}^{T} \;:\!=\; \left( \frac{M_{n,1}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big]}}, \frac{M_{n,2}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big]}} \right)^{\top}\text{ and }\;\overline{\boldsymbol{M}}_{n} \;:\!=\; \bigg( \Big(\overline{\boldsymbol{M}}_{n}^{U}\Big)^{\top}, \Big(\overline{\boldsymbol{M}}_{n}^{L}\Big)^{\top} \bigg)^{\top}.\end{equation*}
\begin{equation*} \overline{\boldsymbol{M}}_{n}^{T} \;:\!=\; \left( \frac{M_{n,1}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big]}}, \frac{M_{n,2}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big]}} \right)^{\top}\text{ and }\;\overline{\boldsymbol{M}}_{n} \;:\!=\; \bigg( \Big(\overline{\boldsymbol{M}}_{n}^{U}\Big)^{\top}, \Big(\overline{\boldsymbol{M}}_{n}^{L}\Big)^{\top} \bigg)^{\top}.\end{equation*}
Lemma 6.2.
Under the assumption of Theorem 2.6(ii),
![]() $\overline{\boldsymbol{M}}_{n} \xrightarrow[n \to \infty]{d} N(\textbf{0},I)$
.
$\overline{\boldsymbol{M}}_{n} \xrightarrow[n \to \infty]{d} N(\textbf{0},I)$
.
Proof of Lemma
6.2. By the Cramér–Wold theorem (see Theorem 29.4 of Billingsley [Reference Billingsley28]), it is enough to show that for
![]() $t_{i}^{T} \in \mathbb{R}$
, where
$t_{i}^{T} \in \mathbb{R}$
, where
![]() $i=1,2$
and
$i=1,2$
and
![]() $T \in \{L,U\}$
,
$T \in \{L,U\}$
,
 \begin{equation} \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{M_{n,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \xrightarrow[n \to \infty]{d} N \Bigg(0,\sum_{T \in \{L,U\}}\sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2} \Bigg).\end{equation}
\begin{equation} \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{M_{n,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \xrightarrow[n \to \infty]{d} N \Bigg(0,\sum_{T \in \{L,U\}}\sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2} \Bigg).\end{equation}
Using Proposition A.3, we see that
 \begin{equation*} \Bigg\{ \Bigg( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} M_{n,i}^{T}, \mathcal{H}_{n,2} \Bigg) \Bigg\}_{n=1}^{\infty}\end{equation*}
\begin{equation*} \Bigg\{ \Bigg( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} M_{n,i}^{T}, \mathcal{H}_{n,2} \Bigg) \Bigg\}_{n=1}^{\infty}\end{equation*}
is a mean-zero martingale sequence. In particular,
 \begin{equation*} \left\{ \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{M_{j,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}}, \mathcal{H}_{j,2} \right) \right\}_{j=1}^{n}\end{equation*}
\begin{equation*} \left\{ \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{M_{j,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}}, \mathcal{H}_{j,2} \right) \right\}_{j=1}^{n}\end{equation*}
is a mean-zero martingale array. We will apply Theorem 3.2 of Hall and Heyde [Reference Hall and Heyde29] with
![]() $k_{n}=n$
,
$k_{n}=n$
,
 \begin{align*}X_{nl}=\sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}},\end{align*}
\begin{align*}X_{nl}=\sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}},\end{align*}
![]() $S_{nj}=\sum_{l=1}^{j} X_{nl}$
,
$S_{nj}=\sum_{l=1}^{j} X_{nl}$
,
![]() $\mathcal{F}_{nj}=\mathcal{H}_{j,2}$
, and
$\mathcal{F}_{nj}=\mathcal{H}_{j,2}$
, and
![]() $B^{2}=\sum_{T \in \{L,U\}}\sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2}$
; from this we will obtain (22). To this end, we need to verify the following conditions:
$B^{2}=\sum_{T \in \{L,U\}}\sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2}$
; from this we will obtain (22). To this end, we need to verify the following conditions:
-
(i)
 $\mathbb{E}\big[\big(S_{nj}\big)^{2}\big] < \infty$
,
$\mathbb{E}\big[\big(S_{nj}\big)^{2}\big] < \infty$
, -
(ii)
 $\max_{l=1,\dots,n} \lvert X_{nl}\rvert \xrightarrow[n \to \infty]{p} 0$
,
$\max_{l=1,\dots,n} \lvert X_{nl}\rvert \xrightarrow[n \to \infty]{p} 0$
, -
(iii)
 $\sum_{l=1}^{n} X_{nl}^{2} \xrightarrow[n \to \infty]{p} B^{2}$
, and
$\sum_{l=1}^{n} X_{nl}^{2} \xrightarrow[n \to \infty]{p} B^{2}$
, and -
(iv)
 $\sup_{n \in \mathbb{N}} \mathbb{E}\big[\!\max_{l=1,\dots,n} X_{nl}^{2}\big] < \infty$
.
$\sup_{n \in \mathbb{N}} \mathbb{E}\big[\!\max_{l=1,\dots,n} X_{nl}^{2}\big] < \infty$
.
Using Proposition A.3 (iv), we have
![]() $\mathbb{E}\big[\big(M_{j,i_{1}}^{T_{1}}\big)\big(M_{j,i_{2}}^{T_{2}}\big)\big]=0$
if either
$\mathbb{E}\big[\big(M_{j,i_{1}}^{T_{1}}\big)\big(M_{j,i_{2}}^{T_{2}}\big)\big]=0$
if either
![]() $T_{1} \neq T_{2}$
or
$T_{1} \neq T_{2}$
or
![]() $i_{1} \neq i_{2}$
, and since
$i_{1} \neq i_{2}$
, and since
![]() $\mathbb{E}\big[\big(M_{j,i}^{T}\big)^{2}\big]$
are non-decreasing in j, we obtain that
$\mathbb{E}\big[\big(M_{j,i}^{T}\big)^{2}\big]$
are non-decreasing in j, we obtain that
 \begin{align*} \mathbb{E} \left[ \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{M_{j,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} \right] &= \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2} \frac{\mathbb{E}\big[\big(M_{j,i}^{T}\big)^{2}\big]}{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]} \\[5pt] &\leq \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2} < \infty,\end{align*}
\begin{align*} \mathbb{E} \left[ \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{M_{j,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} \right] &= \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2} \frac{\mathbb{E}\big[\big(M_{j,i}^{T}\big)^{2}\big]}{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]} \\[5pt] &\leq \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2} < \infty,\end{align*}
which yields Condition (i). Using again that
![]() $\mathbb{E}\big[\big(D_{l,i_{1}}^{T_{1}}\big)\big(D_{l,i_{2}}^{T_{2}}\big)\big]=0$
if either
$\mathbb{E}\big[\big(D_{l,i_{1}}^{T_{1}}\big)\big(D_{l,i_{2}}^{T_{2}}\big)\big]=0$
if either
![]() $T_{1} \neq T_{2}$
or
$T_{1} \neq T_{2}$
or
![]() $i_{1} \neq i_{2}$
and
$i_{1} \neq i_{2}$
and
![]() $\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]=\sum_{l=1}^{n} \mathbb{E}\big[\big(D_{l,i}^{T}\big)^{2}\big]$
, we obtain that
$\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]=\sum_{l=1}^{n} \mathbb{E}\big[\big(D_{l,i}^{T}\big)^{2}\big]$
, we obtain that
 \begin{align*} \mathbb{E} \left[ \max_{l=1,\dots,n} \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} \right] &\leq \mathbb{E} \left[ \sum_{l=1}^{n} \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} \right] \\[5pt] &= \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2},\end{align*}
\begin{align*} \mathbb{E} \left[ \max_{l=1,\dots,n} \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} \right] &\leq \mathbb{E} \left[ \sum_{l=1}^{n} \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} \right] \\[5pt] &= \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2},\end{align*}
yielding Condition (iv). Turning to Condition (ii), assuming without loss of generality that
![]() $t_{i}^{T} \neq 0$
; using that
$t_{i}^{T} \neq 0$
; using that
 \begin{equation*} \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} \leq 4 \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2} \frac{\big(D_{l,i}^{T}\big)^{2}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}},\end{equation*}
\begin{equation*} \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} \leq 4 \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2} \frac{\big(D_{l,i}^{T}\big)^{2}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}},\end{equation*}
we obtain that for all
![]() $\epsilon>0$
,
$\epsilon>0$
,
 \begin{align*} &\mathbb{P}\left( \max_{l=1,\dots,n} \biggl\lvert \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \biggr\rvert \geq \epsilon \right) \\[5pt] \leq &\sum_{l=1}^{n} \mathbb{P}\left( \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} \geq \epsilon^{2} \right) \\[5pt] \leq &\sum_{T \in \{L,U\}} \sum_{i=1}^{2} \sum_{l=1}^{n} \mathbb{P} \bigg( \big(D_{l,i}^{T}\big)^{2} \geq \bigg( \frac{\epsilon}{4 t_{i}^{T}} \bigg)^{2} \mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big] \bigg).\end{align*}
\begin{align*} &\mathbb{P}\left( \max_{l=1,\dots,n} \biggl\lvert \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \biggr\rvert \geq \epsilon \right) \\[5pt] \leq &\sum_{l=1}^{n} \mathbb{P}\left( \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} \geq \epsilon^{2} \right) \\[5pt] \leq &\sum_{T \in \{L,U\}} \sum_{i=1}^{2} \sum_{l=1}^{n} \mathbb{P} \bigg( \big(D_{l,i}^{T}\big)^{2} \geq \bigg( \frac{\epsilon}{4 t_{i}^{T}} \bigg)^{2} \mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big] \bigg).\end{align*}
For
![]() $i=1$
, we use that
$i=1$
, we use that
![]() $\tilde{\chi}_{l-1}^{T} \in \{0,1\}$
and obtain
$\tilde{\chi}_{l-1}^{T} \in \{0,1\}$
and obtain
 \begin{align*} &\sum_{l=1}^{n} \mathbb{P} \biggl( \big(D_{l,1}^{T}\big)^{2} \geq \biggl( \frac{\epsilon}{4t_{1}^{T}} \biggr)^{2} \mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big] \biggr) \\[5pt] \leq\ & \sum_{l=1}^{n} \mathbb{P} \biggl( \big(D_{l,1}^{T}\big)^{2} \geq \biggl( \frac{\epsilon}{4t_{1}^{T}} \biggr)^{2} \mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big] | \tilde{\chi}_{l-1}^{T}=1 \biggr) \\[5pt] =\ & \frac{n}{\mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big]} \mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big]\mathbb{P} \biggl( \Big(\overline{P}_{0}^{T}-M^{T}\Big)^{2} \geq \biggl( \frac{\epsilon}{4t_{1}^{T}} \biggr)^{2} \mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big] \biggr).\end{align*}
\begin{align*} &\sum_{l=1}^{n} \mathbb{P} \biggl( \big(D_{l,1}^{T}\big)^{2} \geq \biggl( \frac{\epsilon}{4t_{1}^{T}} \biggr)^{2} \mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big] \biggr) \\[5pt] \leq\ & \sum_{l=1}^{n} \mathbb{P} \biggl( \big(D_{l,1}^{T}\big)^{2} \geq \biggl( \frac{\epsilon}{4t_{1}^{T}} \biggr)^{2} \mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big] | \tilde{\chi}_{l-1}^{T}=1 \biggr) \\[5pt] =\ & \frac{n}{\mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big]} \mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big]\mathbb{P} \biggl( \Big(\overline{P}_{0}^{T}-M^{T}\Big)^{2} \geq \biggl( \frac{\epsilon}{4t_{1}^{T}} \biggr)^{2} \mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big] \biggr).\end{align*}
It follows from Proposition A.3(i) and Proposition 6.1(i) that
where, for
![]() $T=L$
,
$T=L$
,
![]() $\tilde{\theta}^{L} \;:\!=\; \theta^{L}$
, and since
$\tilde{\theta}^{L} \;:\!=\; \theta^{L}$
, and since
![]() $V_{1}^{T}<\infty$
,
$V_{1}^{T}<\infty$
,
yielding that
For
![]() $i=2$
, we use that if
$i=2$
, we use that if
![]() $\tilde{\chi}_{l-1}^{T}=1$
then
$\tilde{\chi}_{l-1}^{T}=1$
then
![]() $Z_{l-1} \geq 1$
and obtain that
$Z_{l-1} \geq 1$
and obtain that
 \begin{align*} &\sum_{l=1}^{n} \mathbb{P} \biggl( \big(D_{l,2}^{T}\big)^{2} \geq \biggl( \frac{\epsilon}{4t_{2}^{T}} \biggr)^{2} \mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big] \biggr) \\[5pt] \leq& \ n \sup_{z \in \mathbb{N}} \mathbb{P} \biggl( \biggl( \frac{1}{z} \sum_{i=1}^{z} \Big(\xi_{0,i}^{T}-\overline{P}_{0}^{T}\Big) \biggr)^{2} \geq \biggl( \frac{\epsilon}{4t_{2}^{T}} \biggr)^{2} \mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big] \biggr).\end{align*}
\begin{align*} &\sum_{l=1}^{n} \mathbb{P} \biggl( \big(D_{l,2}^{T}\big)^{2} \geq \biggl( \frac{\epsilon}{4t_{2}^{T}} \biggr)^{2} \mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big] \biggr) \\[5pt] \leq& \ n \sup_{z \in \mathbb{N}} \mathbb{P} \biggl( \biggl( \frac{1}{z} \sum_{i=1}^{z} \Big(\xi_{0,i}^{T}-\overline{P}_{0}^{T}\Big) \biggr)^{2} \geq \biggl( \frac{\epsilon}{4t_{2}^{T}} \biggr)^{2} \mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big] \biggr).\end{align*}
Next, using Proposition A.3(ii) and Proposition 6.1(ii)–(iii), we have that
 \begin{equation} \lim_{n \to \infty} \frac{n}{\mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big]} \leq \frac{\mu^{U}+\mu^{L}}{V_{2}^{T} \tilde{A}^{T}}< \infty,\end{equation}
\begin{equation} \lim_{n \to \infty} \frac{n}{\mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big]} \leq \frac{\mu^{U}+\mu^{L}}{V_{2}^{T} \tilde{A}^{T}}< \infty,\end{equation}
where
![]() $\tilde{A}^{L} \;:\!=\; A^{L}$
. Since by Jensen’s inequality
$\tilde{A}^{L} \;:\!=\; A^{L}$
. Since by Jensen’s inequality
using the Markov inequality, we obtain
which yields that
For (iii), we decompose
 \begin{equation*} \sum_{l=1}^{n} \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} - \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2}\end{equation*}
\begin{equation*} \sum_{l=1}^{n} \left( \sum_{T \in \{L,U\}} \sum_{i=1}^{2} t_{i}^{T} \frac{D_{l,i}^{T}}{\sqrt{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}} \right)^{2} - \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2}\end{equation*}
as
 \begin{equation} \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2} \frac{\sum_{l=1}^{n} \big(D_{l,i}^{T}\big)^{2}-\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]} + \sum_{T_{1} \neq T_{2} \text{ or } i_{1} \neq i_{2}} t_{i_{1}}^{T_{1}} t_{i_{2}}^{T_{2}} \frac{\sum_{l=1}^{n} \big(D_{l,i_{1}}^{T_{1}}\big) \big(D_{l,i_{2}}^{T_{2}}\big)}{\sqrt{\mathbb{E}\big[\big(M_{n,i_{1}}^{T_{1}}\big)^{2}\big] \mathbb{E}\big[\big(M_{n,i_{2}}^{T_{2}}\big)^{2}\big]}}\end{equation}
\begin{equation} \sum_{T \in \{L,U\}} \sum_{i=1}^{2} \big(t_{i}^{T}\big)^{2} \frac{\sum_{l=1}^{n} \big(D_{l,i}^{T}\big)^{2}-\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]}{\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]} + \sum_{T_{1} \neq T_{2} \text{ or } i_{1} \neq i_{2}} t_{i_{1}}^{T_{1}} t_{i_{2}}^{T_{2}} \frac{\sum_{l=1}^{n} \big(D_{l,i_{1}}^{T_{1}}\big) \big(D_{l,i_{2}}^{T_{2}}\big)}{\sqrt{\mathbb{E}\big[\big(M_{n,i_{1}}^{T_{1}}\big)^{2}\big] \mathbb{E}\big[\big(M_{n,i_{2}}^{T_{2}}\big)^{2}\big]}}\end{equation}
and show that each of the above terms converges to zero with probability one. Since
![]() $\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]=\sum_{l=1}^{n} \mathbb{E}[\big(D_{l,i}^{T}\big)^{2}]$
, we use Proposition A.3(iii) and obtain that
$\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]=\sum_{l=1}^{n} \mathbb{E}[\big(D_{l,i}^{T}\big)^{2}]$
, we use Proposition A.3(iii) and obtain that
 \begin{align*}\left\{ \left(\sum_{l=1}^{n} \big(\big(D_{l,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{l,i}^{T}\big)^{2}\big]\big), \tilde{\mathcal{H}}_{n,i}\right) \right\}_{n=1}^{\infty}\end{align*}
\begin{align*}\left\{ \left(\sum_{l=1}^{n} \big(\big(D_{l,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{l,i}^{T}\big)^{2}\big]\big), \tilde{\mathcal{H}}_{n,i}\right) \right\}_{n=1}^{\infty}\end{align*}
are mean-zero martingale sequences, and for
![]() $s = 1+\delta/2$
,
$s = 1+\delta/2$
,
We use (23) and (24), and apply Theorem 2.18 of Hall and Heyde [Reference Hall and Heyde29] with
![]() $S_{n}=\sum_{l=1}^{n} \big(\big(D_{l,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{l,i}^{T}\big)^{2}\big]\big)$
,
$S_{n}=\sum_{l=1}^{n} \big(\big(D_{l,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{l,i}^{T}\big)^{2}\big]\big)$
,
![]() $X_{l}=\big(D_{l,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{l,i}^{T}\big)^{2}\big]$
,
$X_{l}=\big(D_{l,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{l,i}^{T}\big)^{2}\big]$
,
![]() $\mathcal{F}_{n} = \tilde{\mathcal{H}}_{n,i}$
,
$\mathcal{F}_{n} = \tilde{\mathcal{H}}_{n,i}$
,
![]() $U_{n}=\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]$
, and
$U_{n}=\mathbb{E}\big[\big(M_{n,i}^{T}\big)^{2}\big]$
, and
![]() $p=s$
, where
$p=s$
, where
![]() $i=1,2$
, to obtain the convergence of the first term in (25). For the second term we proceed similarly. Specifically, using Proposition A.3(iv) and the Cauchy–Schwartz inequality, we obtain that
$i=1,2$
, to obtain the convergence of the first term in (25). For the second term we proceed similarly. Specifically, using Proposition A.3(iv) and the Cauchy–Schwartz inequality, we obtain that
![]() $\big\{ \big(\sum_{l=1}^{n} \big(D_{l,i_{1}}^{T_{1}}\big)\big(D_{l,i_{2}}^{T_{2}}\big), \tilde{\mathcal{H}}_{n,2}\big) \big\}_{n=0}^{\infty}$
is a mean-zero martingale sequence, and for
$\big\{ \big(\sum_{l=1}^{n} \big(D_{l,i_{1}}^{T_{1}}\big)\big(D_{l,i_{2}}^{T_{2}}\big), \tilde{\mathcal{H}}_{n,2}\big) \big\}_{n=0}^{\infty}$
is a mean-zero martingale sequence, and for
![]() $s = 1+\delta/2$
,
$s = 1+\delta/2$
,
Finally, we apply Theorem 2.18 of Hall and Heyde [Reference Hall and Heyde29] with
![]() $S_{n}=\sum_{l=1}^{n} \Big(D_{l,i_{1}}^{T_{1}}\Big)\Big(D_{l,i_{2}}^{T_{2}}\Big)$
,
$S_{n}=\sum_{l=1}^{n} \Big(D_{l,i_{1}}^{T_{1}}\Big)\Big(D_{l,i_{2}}^{T_{2}}\Big)$
,
![]() $X_{l}=\Big(D_{l,i_{1}}^{T_{1}}\Big)\Big(D_{l,i_{2}}^{T_{2}}\Big)$
,
$X_{l}=\Big(D_{l,i_{1}}^{T_{1}}\Big)\Big(D_{l,i_{2}}^{T_{2}}\Big)$
,
![]() $\mathcal{F}_{n} = \tilde{\mathcal{H}}_{n,2}$
,
$\mathcal{F}_{n} = \tilde{\mathcal{H}}_{n,2}$
,
![]() $U_{n}=\sqrt{\mathbb{E}\Big[\Big(M_{n,i_{1}}^{T_{1}}\Big)^{2}\Big] \mathbb{E}\big[\big(M_{n,i_{2}}^{T_{2}}\big)^{2}\big]}$
, and
$U_{n}=\sqrt{\mathbb{E}\Big[\Big(M_{n,i_{1}}^{T_{1}}\Big)^{2}\Big] \mathbb{E}\big[\big(M_{n,i_{2}}^{T_{2}}\big)^{2}\big]}$
, and
![]() $p=s$
, from which we obtain convergence of the second term in (25).
$p=s$
, from which we obtain convergence of the second term in (25).
We are now ready to prove the main result of the section.
Proof of Theorem
2.6. Using Proposition A.3(i)–(ii) and
![]() $\tilde{\chi}_{j-1}^{T} \leq 1$
, we obtain that for
$\tilde{\chi}_{j-1}^{T} \leq 1$
, we obtain that for
![]() $i=1,2$
,
$i=1,2$
,
![]() $\big\{ \big(M_{n,i}^{T}, \mathcal{H}_{n,i}\big) \big\}_{n=1}^{\infty}$
are martingales and
$\big\{ \big(M_{n,i}^{T}, \mathcal{H}_{n,i}\big) \big\}_{n=1}^{\infty}$
are martingales and
 \begin{equation*} \sum_{j=1}^{\infty} \frac{1}{j^{s}} \mathbb{E}\big[ \big\lvert D_{j,i}^{T}\big\rvert^{s} | \mathcal{H}_{j-1,i} \big] \leq \mathbb{E}\big[\Lambda_{0,i}^{T,s}\big] \sum_{j=1}^{\infty} \frac{1}{j^{s}} < \infty.\end{equation*}
\begin{equation*} \sum_{j=1}^{\infty} \frac{1}{j^{s}} \mathbb{E}\big[ \big\lvert D_{j,i}^{T}\big\rvert^{s} | \mathcal{H}_{j-1,i} \big] \leq \mathbb{E}\big[\Lambda_{0,i}^{T,s}\big] \sum_{j=1}^{\infty} \frac{1}{j^{s}} < \infty.\end{equation*}
We apply Theorem 2.18 of Hall and Heyde [Reference Hall and Heyde29] with
![]() $S_{n}=M_{n,i}^{T}$
,
$S_{n}=M_{n,i}^{T}$
,
![]() $X_{j}=D_{j,i}^{T}$
, where
$X_{j}=D_{j,i}^{T}$
, where
![]() $i=1,2$
and
$i=1,2$
and
![]() $T \in \{ L, U \}$
, and with
$T \in \{ L, U \}$
, and with
![]() $U_{n}=n$
,
$U_{n}=n$
,
![]() $p=s$
, and
$p=s$
, and
![]() $\mathcal{F}_{n} = \mathcal{H}_{n,1}$
for
$\mathcal{F}_{n} = \mathcal{H}_{n,1}$
for
![]() $i=1$
and
$i=1$
and
![]() $\mathcal{F}_{n} = \mathcal{H}_{n,2}$
for
$\mathcal{F}_{n} = \mathcal{H}_{n,2}$
for
![]() $i=2$
, From this we obtain that
$i=2$
, From this we obtain that
![]() $\lim_{n \to \infty} \frac{1}{n} M_{n,i}^T = 0$
a.s. From this, Theorem 2.5, and Proposition 6.1(i), we obtain that
$\lim_{n \to \infty} \frac{1}{n} M_{n,i}^T = 0$
a.s. From this, Theorem 2.5, and Proposition 6.1(i), we obtain that
![]() $\lim_{n \to \infty} \frac{1}{\tilde{C}_{n}^T} M_{n,i}^T = 0$
a.s. Using (20) we conclude that
$\lim_{n \to \infty} \frac{1}{\tilde{C}_{n}^T} M_{n,i}^T = 0$
a.s. Using (20) we conclude that
![]() $\lim_{n \to \infty} M_{n}^{T}=M^{T}$
a.s. Turning to the central limit theorem, Lemma 6.2(iii) yields that
$\lim_{n \to \infty} M_{n}^{T}=M^{T}$
a.s. Turning to the central limit theorem, Lemma 6.2(iii) yields that
 \begin{equation*}\overline{\boldsymbol{M}}_{n} = \left( \frac{M_{n,1}^{U}}{\sqrt{\mathbb{E}\big[\big(M_{n,1}^{U}\big)^{2}\big]}}, \frac{M_{n,2}^{U}}{\sqrt{\mathbb{E}\big[\big(M_{n,2}^{U}\big)^{2}\big]}}, \frac{M_{n,1}^{L}}{\sqrt{\mathbb{E}\big[\big(M_{n,1}^{L}\big)^{2}\big]}}, \frac{M_{n,2}^{L}}{\sqrt{\mathbb{E}\big[\big(M_{n,2}^{L}\big)^{2}\big]}} \right)^{\top}\end{equation*}
\begin{equation*}\overline{\boldsymbol{M}}_{n} = \left( \frac{M_{n,1}^{U}}{\sqrt{\mathbb{E}\big[\big(M_{n,1}^{U}\big)^{2}\big]}}, \frac{M_{n,2}^{U}}{\sqrt{\mathbb{E}\big[\big(M_{n,2}^{U}\big)^{2}\big]}}, \frac{M_{n,1}^{L}}{\sqrt{\mathbb{E}\big[\big(M_{n,1}^{L}\big)^{2}\big]}}, \frac{M_{n,2}^{L}}{\sqrt{\mathbb{E}\big[\big(M_{n,2}^{L}\big)^{2}\big]}} \right)^{\top}\end{equation*}
is asymptotically normal with mean zero and identity covariance matrix. Let
![]() $D_{n}^{2}$
be the
$D_{n}^{2}$
be the
![]() $4 \times 4$
diagonal matrix
$4 \times 4$
diagonal matrix
 \begin{equation*} D_{n}^{2} \;:\!=\; \textrm{Diag} \left( \frac{n\mathbb{E}\big[\big(M_{n,1}^{U}\big)^{2}\big]}{\big(\tilde{C}_{n}^U\big)^{2}}, \frac{n\mathbb{E}\big[\big(M_{n,2}^{U}\big)^{2}\big]}{\big(\tilde{C}_{n}^U\big)^{2}}, \frac{n\mathbb{E}\big[\big(M_{n,1}^{L}\big)^{2}\big]}{\big(\tilde{C}_{n}^L\big)^{2}}, \frac{n\mathbb{E}\big[\big(M_{n,2}^{L}\big)^{2}\big]}{\big(\tilde{C}_{n}^L\big)^{2}} \right).\end{equation*}
\begin{equation*} D_{n}^{2} \;:\!=\; \textrm{Diag} \left( \frac{n\mathbb{E}\big[\big(M_{n,1}^{U}\big)^{2}\big]}{\big(\tilde{C}_{n}^U\big)^{2}}, \frac{n\mathbb{E}\big[\big(M_{n,2}^{U}\big)^{2}\big]}{\big(\tilde{C}_{n}^U\big)^{2}}, \frac{n\mathbb{E}\big[\big(M_{n,1}^{L}\big)^{2}\big]}{\big(\tilde{C}_{n}^L\big)^{2}}, \frac{n\mathbb{E}\big[\big(M_{n,2}^{L}\big)^{2}\big]}{\big(\tilde{C}_{n}^L\big)^{2}} \right).\end{equation*}
By Proposition A.3(i)–(ii) and Proposition 6.1,
![]() $D_{n} \overline{\boldsymbol{M}}_{n}$
is asymptotically normal with mean zero and covariance matrix
$D_{n} \overline{\boldsymbol{M}}_{n}$
is asymptotically normal with mean zero and covariance matrix
Using the continuous mapping theorem, it follows that
7. Discussion and concluding remarks
In this paper we have developed the BPRE with thresholds to describe periods of growth and decrease in the population size arising in several applications, including COVID dynamics. Even though the model is non-Markov, we identify Markov subsequences and use them to understand the length of time the process spends in the supercritical and subcritical regimes. Furthermore, using the regeneration technique, we also study the rate of growth (resp. decline) of the process in the supercritical (resp. subcritical) regime. It is possible to start the process using the subcritical BPRE and then move to the supercritical regime; this introduces only minor changes, and the qualitative results remain the same. Finally, we note that without the incorporation of immigration in the supercritical regime, the process will become extinct with probability one, and hence the cyclical path behavior may not be observed.
An interesting question concerns the choice of strongly subcritical BPRE for the subcritical regime. It is folklore that the generation sizes of moderately and weakly subcritical processes can increase for long periods of time, and in that case the time needed to cross the lower threshold will have a heavier tail. This could lead to a lack of identifiability of the supercritical and subcritical regimes. Similar issues arise when a subcritical BPRE is replaced by a critical BPRE or when immigration is allowed in both regimes. Since a subcritical BPRE with immigration converges in distribution to a proper limit law [Reference Roitershtein30], we may fail to observe a clear period of decrease. The path properties of these alternatives could be useful for modeling other dynamics observed (see [Reference Klebaner9, Reference Iannelli and Pugliese12]). Mathematical issues arising from these alternatives would involve different techniques from those used in this paper.
We end this section with a brief discussion concerning the moment conditions in Theorem 2.6. It is possible to reduce the conditions
![]() $\mathbb{E}\big[ \Lambda_{0,i}^{T,2+\delta}\big] < \infty$
to a finite-second-moment hypothesis. This requires an extension of Lemma 4.1 to joint independence of blocks in
$\mathbb{E}\big[ \Lambda_{0,i}^{T,2+\delta}\big] < \infty$
to a finite-second-moment hypothesis. This requires an extension of Lemma 4.1 to joint independence of blocks in
![]() $B_{i,l}^{L}$
,
$B_{i,l}^{L}$
,
![]() $B_{i,l}^{U}$
, offspring random variables, environments, and immigration over cycles. The proof will require the Markov property of the pair
$B_{i,l}^{U}$
, offspring random variables, environments, and immigration over cycles. The proof will require the Markov property of the pair
![]() $\big\{ \big(Z_{\nu_{j-1}},Z_{\tau_{j}}\big) \big\}_{j=1}^{\infty}$
and its uniform ergodicity. The joint Markov property will also yield a joint central limit theorem for the length and proportion of time spent in the supercritical and subcritical regimes. The proof is similar to that of Theorem 2.3 and Lemma 4.1, but is more cumbersome, with an increased notational burden. The numerical experiments suggest that the estimators of the mean parameters of the supercritical and subcritical regimes are not affected by the choice of various distributions. A thorough statistical analysis of the robustness of the estimators and an analysis of the datasets are beyond the scope of this paper and will be undertaken elsewhere.
$\big\{ \big(Z_{\nu_{j-1}},Z_{\tau_{j}}\big) \big\}_{j=1}^{\infty}$
and its uniform ergodicity. The joint Markov property will also yield a joint central limit theorem for the length and proportion of time spent in the supercritical and subcritical regimes. The proof is similar to that of Theorem 2.3 and Lemma 4.1, but is more cumbersome, with an increased notational burden. The numerical experiments suggest that the estimators of the mean parameters of the supercritical and subcritical regimes are not affected by the choice of various distributions. A thorough statistical analysis of the robustness of the estimators and an analysis of the datasets are beyond the scope of this paper and will be undertaken elsewhere.
Appendix A. Auxiliary results
This section contains detailed descriptions and proofs of auxiliary results used in the paper. We begin with a detailed description of the probability space for the BPRET.
A.1. Probability space
In this subsection we describe in detail the random variables used to define the BPRET, as well as the underlying probability space. The thresholds
![]() $\{ (U_{j},L_{j})\}_{j=1}^{\infty}$
are i.i.d. random vectors with support
$\{ (U_{j},L_{j})\}_{j=1}^{\infty}$
are i.i.d. random vectors with support
![]() $S_{B}^{U} \times S_{B}^{L}$
, where
$S_{B}^{U} \times S_{B}^{L}$
, where
![]() $S_{B}^{U} = \mathbb{N} \cap [L_U+1,\infty)$
,
$S_{B}^{U} = \mathbb{N} \cap [L_U+1,\infty)$
,
![]() $S_{B}^{L} = \mathbb{N} \cap [L_{0}, L_{U}]$
, and
$S_{B}^{L} = \mathbb{N} \cap [L_{0}, L_{U}]$
, and
![]() $1 \leq L_{0} \leq L_{U}$
are fixed integers, defined on the probability space
$1 \leq L_{0} \leq L_{U}$
are fixed integers, defined on the probability space
![]() $(\Omega_{B},\mathcal{F}_{B},\mathbb{P}_{B})$
. Next,
$(\Omega_{B},\mathcal{F}_{B},\mathbb{P}_{B})$
. Next,
![]() $\Pi^{L} = \{ \Pi_{n}^{L} \}_{n=0}^{\infty}$
and
$\Pi^{L} = \{ \Pi_{n}^{L} \}_{n=0}^{\infty}$
and
![]() $\Pi^{U} = \{ \Pi_{n}^{U} \}_{n=0}^{\infty}$
are subcritical and supercritical environmental sequences that are defined on probability spaces
$\Pi^{U} = \{ \Pi_{n}^{U} \}_{n=0}^{\infty}$
are subcritical and supercritical environmental sequences that are defined on probability spaces
![]() $(\Omega_{E^{L}}, \mathcal{F}_{E^{L}}, \mathbb{P}_{E^{L}})$
and
$(\Omega_{E^{L}}, \mathcal{F}_{E^{L}}, \mathbb{P}_{E^{L}})$
and
![]() $(\Omega_{E^{U}}, \mathcal{F}_{E^{U}}, \mathbb{P}_{E^{U}})$
. Specifically,
$(\Omega_{E^{U}}, \mathcal{F}_{E^{U}}, \mathbb{P}_{E^{U}})$
. Specifically,
![]() $\Pi_{n}^{U}=\big(P_{n}^{U},Q_{n}^{U}\big)$
and
$\Pi_{n}^{U}=\big(P_{n}^{U},Q_{n}^{U}\big)$
and
![]() $\Pi_{n}^{L}=P_{n}^{L}$
, where
$\Pi_{n}^{L}=P_{n}^{L}$
, where
![]() $P_{n}^{U}=\{ P_{n,r}^{U} \}_{r=0}^{\infty}$
,
$P_{n}^{U}=\{ P_{n,r}^{U} \}_{r=0}^{\infty}$
,
![]() $P_{n}^{L}=\{ P_{n,r}^{L} \}_{r=0}^{\infty}$
, and
$P_{n}^{L}=\{ P_{n,r}^{L} \}_{r=0}^{\infty}$
, and
![]() $Q_{n}^{U}=\{ Q_{n,r}^{U} \}_{r=0}^{\infty}$
are probability distributions in
$Q_{n}^{U}=\{ Q_{n,r}^{U} \}_{r=0}^{\infty}$
are probability distributions in
![]() $\mathcal{P}$
. Let
$\mathcal{P}$
. Let
![]() $(\Omega_{U},\mathcal{F}_{U},\mathbb{P}_{U})$
and
$(\Omega_{U},\mathcal{F}_{U},\mathbb{P}_{U})$
and
![]() $(\Omega_{L},\mathcal{F}_{L},\mathbb{P}_{L})$
denote probability spaces corresponding to the supercritical BPRE with immigration and the subcritical BPRE. Hence, the environment sequence
$(\Omega_{L},\mathcal{F}_{L},\mathbb{P}_{L})$
denote probability spaces corresponding to the supercritical BPRE with immigration and the subcritical BPRE. Hence, the environment sequence
![]() $\Pi^{U} = \{ \Pi_{n}^{U} \}_{n=0}^{\infty}$
, the offspring sequence
$\Pi^{U} = \{ \Pi_{n}^{U} \}_{n=0}^{\infty}$
, the offspring sequence
![]() $\{ \xi_{n,i}^{U} \}_{i=1}^{\infty}$
, and the immigration sequence
$\{ \xi_{n,i}^{U} \}_{i=1}^{\infty}$
, and the immigration sequence
![]() $\{ I_{n}^{U} \}_{n=0}^{\infty}$
are random variables on
$\{ I_{n}^{U} \}_{n=0}^{\infty}$
are random variables on
![]() $(\Omega_{U},\mathcal{F}_{U},\mathbb{P}_{U})$
. Similarly,
$(\Omega_{U},\mathcal{F}_{U},\mathbb{P}_{U})$
. Similarly,
![]() $\Pi^{L} = \{ \Pi_{n}^{L} \}_{n=0}^{\infty}$
and
$\Pi^{L} = \{ \Pi_{n}^{L} \}_{n=0}^{\infty}$
and
![]() $\{ \xi_{n,i}^{L} \}_{i=1}^{\infty}$
,
$\{ \xi_{n,i}^{L} \}_{i=1}^{\infty}$
,
![]() $n \geq 0$
, are random variables on
$n \geq 0$
, are random variables on
![]() $(\Omega_{L},\mathcal{F}_{L},\mathbb{P}_{L})$
. We point out here that the probability spaces
$(\Omega_{L},\mathcal{F}_{L},\mathbb{P}_{L})$
. We point out here that the probability spaces
![]() $(\Omega_{U},\mathcal{F}_{U},\mathbb{P}_{U})$
and
$(\Omega_{U},\mathcal{F}_{U},\mathbb{P}_{U})$
and
![]() $(\Omega_{E^{U}},\mathcal{F}_{E^{U}},\mathbb{P}_{E^{U}})$
are linked; that is, for all integrable functions
$(\Omega_{E^{U}},\mathcal{F}_{E^{U}},\mathbb{P}_{E^{U}})$
are linked; that is, for all integrable functions
![]() $H: \Omega_{U} \to \mathbb{R}$
,
$H: \Omega_{U} \to \mathbb{R}$
,
Similar comments also hold with U replaced by L in the above. All of the random variables described above are defined on the probability space
![]() $(\Omega,\mathcal{F},\mathbb{P}) = (\Omega_{B} \times \Omega_{U} \times \Omega_{L}, \mathcal{F}_{B} \otimes \mathcal{F}_{U} \otimes \mathcal{F}_{L}, \mathbb{P}_{B} \times \mathbb{P}_{U} \times \mathbb{P}_{L})$
.
$(\Omega,\mathcal{F},\mathbb{P}) = (\Omega_{B} \times \Omega_{U} \times \Omega_{L}, \mathcal{F}_{B} \otimes \mathcal{F}_{U} \otimes \mathcal{F}_{L}, \mathbb{P}_{B} \times \mathbb{P}_{U} \times \mathbb{P}_{L})$
.
A.2. Time-homogeneity of
 $\{Z_{\nu_{j}}\}_{j=0}^{\infty}$
and
$\{Z_{\nu_{j}}\}_{j=0}^{\infty}$
and
 $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
Lemma A.1.
Assume (
H1
) and (
H2′
). For all
![]() $i \in S^{L}$
,
$i \in S^{L}$
,
![]() $k \in S^{U}$
, and
$k \in S^{U}$
, and
![]() $j \in \mathbb{N}_{0}$
, the following holds:
$j \in \mathbb{N}_{0}$
, the following holds:
 \begin{align*} \text{(i) } &\mathbb{P}\big(Z_{\tau_{j+1}} = k | Z_{\nu_{j}}=i, \nu_{j}<\infty\big) = \mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}} = k\big) \quad \text{ and} \\[5pt] &\mathbb{P}\big(Z_{\tau_{j+1}} = k | \tau_{j+1}<\infty, Z_{\nu_{j}}=i\big) = \mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}} = k | \tau_{1}< \infty\big), \quad \text{ and} \\[5pt] \text{(ii) } &\mathbb{P}\big(Z_{\nu_{j+1}}=i | Z_{\tau_{j+1}}=k, \tau_{j+1} < \infty\big)=\mathbb{P}_{\delta_{k}^{U}}\big(Z_{\nu_{1}}=i | \tau_{1} < \infty\big) \quad \text{ and } \\[5pt] &\mathbb{P}\big(Z_{\nu_{j+1}}=i | \nu_{j+1} < \infty, Z_{\tau_{j+1}}=k\big)=\mathbb{P}_{\delta_{k}^{U}}\big(Z_{\nu_{1}}=i | \nu_{1}< \infty\big).\end{align*}
\begin{align*} \text{(i) } &\mathbb{P}\big(Z_{\tau_{j+1}} = k | Z_{\nu_{j}}=i, \nu_{j}<\infty\big) = \mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}} = k\big) \quad \text{ and} \\[5pt] &\mathbb{P}\big(Z_{\tau_{j+1}} = k | \tau_{j+1}<\infty, Z_{\nu_{j}}=i\big) = \mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}} = k | \tau_{1}< \infty\big), \quad \text{ and} \\[5pt] \text{(ii) } &\mathbb{P}\big(Z_{\nu_{j+1}}=i | Z_{\tau_{j+1}}=k, \tau_{j+1} < \infty\big)=\mathbb{P}_{\delta_{k}^{U}}\big(Z_{\nu_{1}}=i | \tau_{1} < \infty\big) \quad \text{ and } \\[5pt] &\mathbb{P}\big(Z_{\nu_{j+1}}=i | \nu_{j+1} < \infty, Z_{\tau_{j+1}}=k\big)=\mathbb{P}_{\delta_{k}^{U}}\big(Z_{\nu_{1}}=i | \nu_{1}< \infty\big).\end{align*}
If additionally (
H3
) holds, then (iii)
![]() $\tau_{j}$
and
$\tau_{j}$
and
![]() $\nu_{j}$
are finite a.s.,
$\nu_{j}$
are finite a.s.,
 \begin{align*} &\mathbb{P}\big(Z_{\tau_{j+1}} = k | Z_{\nu_{j}}=i\big) = \mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}} = k\big), \quad \text{ and } \\[5pt] &\mathbb{P}\big(Z_{\nu_{j+1}}=i | Z_{\tau_{j+1}}=k\big)=\mathbb{P}_{\delta_{k}^{U}}\big(Z_{\nu_{1}}=i\big).\end{align*}
\begin{align*} &\mathbb{P}\big(Z_{\tau_{j+1}} = k | Z_{\nu_{j}}=i\big) = \mathbb{P}_{\delta_{i}^{L}}\big(Z_{\tau_{1}} = k\big), \quad \text{ and } \\[5pt] &\mathbb{P}\big(Z_{\nu_{j+1}}=i | Z_{\tau_{j+1}}=k\big)=\mathbb{P}_{\delta_{k}^{U}}\big(Z_{\nu_{1}}=i\big).\end{align*}
Proof of Lemma
A.1. We only prove (i) and (iii). Since
![]() $\mathbb{P}\big(Z_{\tau_{j+1}} = k | Z_{\nu_{j}}=i, \nu_{j}<\infty\big)$
is equal to
$\mathbb{P}\big(Z_{\tau_{j+1}} = k | Z_{\nu_{j}}=i, \nu_{j}<\infty\big)$
is equal to
it is enough to show that for all
![]() $s \geq 1$
and
$s \geq 1$
and
![]() $u \geq L_{U}+1$
,
$u \geq L_{U}+1$
,
 \begin{equation} \begin{aligned} &\mathbb{P}\big(Z_{\nu_{j}+s}=k, Z_{\nu_{j}+s-1}<u, \dots, Z_{\nu_{j}+1}<u | Z_{\nu_{j}}=i, \nu_{j}<\infty \big) \\[5pt] =\ & \mathbb{P}_{\delta_{i}^{L}}(Z_{s}=k, Z_{s-1}<u, \dots, Z_{1}<u).\end{aligned}\end{equation}
\begin{equation} \begin{aligned} &\mathbb{P}\big(Z_{\nu_{j}+s}=k, Z_{\nu_{j}+s-1}<u, \dots, Z_{\nu_{j}+1}<u | Z_{\nu_{j}}=i, \nu_{j}<\infty \big) \\[5pt] =\ & \mathbb{P}_{\delta_{i}^{L}}(Z_{s}=k, Z_{s-1}<u, \dots, Z_{1}<u).\end{aligned}\end{equation}
To this end, we condition on
![]() $\Pi_{\nu_{j}+l}^{U}=\big(p_{l}^{U},q_{l}^{U}\big)$
and
$\Pi_{\nu_{j}+l}^{U}=\big(p_{l}^{U},q_{l}^{U}\big)$
and
![]() $\Pi_{l}^{U}=\big(p_{l}^{U},q_{l}^{U}\big)$
, where
$\Pi_{l}^{U}=\big(p_{l}^{U},q_{l}^{U}\big)$
, where
![]() $l=0,1,\dots,s-1$
. Since, given
$l=0,1,\dots,s-1$
. Since, given
![]() $\Pi_{\nu_{j}+l}^{U}=\big(p_{l}^{U},q_{l}^{U}\big)$
and
$\Pi_{\nu_{j}+l}^{U}=\big(p_{l}^{U},q_{l}^{U}\big)$
and
![]() $\Pi_{l}^{U}=\big(p_{l}^{U},q_{l}^{U}\big)$
, both the sequences
$\Pi_{l}^{U}=\big(p_{l}^{U},q_{l}^{U}\big)$
, both the sequences
![]() $\big\{ \xi_{\nu_{j}+l,i}^{U} \big\}_{i=1}^{\infty}$
,
$\big\{ \xi_{\nu_{j}+l,i}^{U} \big\}_{i=1}^{\infty}$
,
![]() $\{ \xi_{l,i}^{U} \}_{i=1}^{\infty}$
and the random variables
$\{ \xi_{l,i}^{U} \}_{i=1}^{\infty}$
and the random variables
![]() $I_{\nu_{j}+l}^{U}$
,
$I_{\nu_{j}+l}^{U}$
,
![]() $I_{l}^{U}$
are i.i.d., we obtain from (1) that
$I_{l}^{U}$
are i.i.d., we obtain from (1) that
 \begin{align*} &\mathbb{P}\big(Z_{\nu_{j}+s}=k, Z_{\nu_{j}+s-1}<u, \dots, Z_{\nu_{j}+1}<u | Z_{\nu_{j}}=i, \nu_{j}<\infty, \big\{\Pi_{\nu_{j}+l}^{U}\big\}_{l=0}^{s-1}=\big\{\big(p_{l}^{U},q_{l}^{U}\big)\big\}_{l=0}^{s-1} \big) \\[5pt] =\ &\mathbb{P}_{\delta_{i}^{L}}\big(Z_{s}=k, Z_{s-1}<u, \dots, Z_{1}<u | \big\{ \Pi_{l}^{U} \big\}_{l=0}^{s-1}=\big\{ \big(p_{l}^{U},q_{l}^{U}\big)\big\}_{l=0}^{s-1}\big).\end{align*}
\begin{align*} &\mathbb{P}\big(Z_{\nu_{j}+s}=k, Z_{\nu_{j}+s-1}<u, \dots, Z_{\nu_{j}+1}<u | Z_{\nu_{j}}=i, \nu_{j}<\infty, \big\{\Pi_{\nu_{j}+l}^{U}\big\}_{l=0}^{s-1}=\big\{\big(p_{l}^{U},q_{l}^{U}\big)\big\}_{l=0}^{s-1} \big) \\[5pt] =\ &\mathbb{P}_{\delta_{i}^{L}}\big(Z_{s}=k, Z_{s-1}<u, \dots, Z_{1}<u | \big\{ \Pi_{l}^{U} \big\}_{l=0}^{s-1}=\big\{ \big(p_{l}^{U},q_{l}^{U}\big)\big\}_{l=0}^{s-1}\big).\end{align*}
By taking the expectation with respect to
![]() $\Pi^{U}=\{ \Pi_{n}^{U} \}_{n=0}^{\infty}$
and using that the
$\Pi^{U}=\{ \Pi_{n}^{U} \}_{n=0}^{\infty}$
and using that the
![]() $\Pi_{n}^{U}$
are i.i.d., we obtain (26). Next, we notice that
$\Pi_{n}^{U}$
are i.i.d., we obtain (26). Next, we notice that
is positive because
![]() $M^{U} >1$
. It follows from Part (i) that
$M^{U} >1$
. It follows from Part (i) that
![]() $\mathbb{P}\big(Z_{\tau_{j+1}} = k | \tau_{j+1}<\infty, Z_{\nu_{j}}=i\big)=\mathbb{P}_{\delta_{i}^{L}}(Z_{\tau_{1}} = k | \tau_{1}<\infty)$
. Finally, (iii) follows from (i) and (ii) using (3) and (4).
$\mathbb{P}\big(Z_{\tau_{j+1}} = k | \tau_{j+1}<\infty, Z_{\nu_{j}}=i\big)=\mathbb{P}_{\delta_{i}^{L}}(Z_{\tau_{1}} = k | \tau_{1}<\infty)$
. Finally, (iii) follows from (i) and (ii) using (3) and (4).
A.3. Finiteness of
 $\overline{\pi}^{U}$
$\overline{\pi}^{U}$
We show that the stationary distribution
![]() $\pi^{U}$
of the Markov chain
$\pi^{U}$
of the Markov chain
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
has a finite first moment
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
has a finite first moment
![]() $\overline{\pi}^{U}$
.
$\overline{\pi}^{U}$
.
Proposition A.1.
Under (
H1
)–(
H4
), (
H6
) (or (
H7
)), and (
H9
),
![]() $\overline{\pi}^{U} < \infty$
.
$\overline{\pi}^{U} < \infty$
.
Proof of Proposition
A.1. Using that
![]() $\pi^{U}=\{ \pi_{k}^{U} \}_{k \in S^{U}}$
is the stationary distribution of the Markov chain
$\pi^{U}=\{ \pi_{k}^{U} \}_{k \in S^{U}}$
is the stationary distribution of the Markov chain
![]() $\{ Z_{\tau_{j}}\}_{j=1}^{\infty}$
, for all
$\{ Z_{\tau_{j}}\}_{j=1}^{\infty}$
, for all
![]() $k \in S^{U}$
we write
$k \in S^{U}$
we write
![]() $\pi_{k}^{U}=\mathbb{P}_{\pi^{U}}(Z_{\tau_{2}}=k) = \mathbb{E}[ \mathbb{P}_{\pi^{U}}(Z_{\tau_{2}}=k | U_{2})]$
. Next, we notice that
$\pi_{k}^{U}=\mathbb{P}_{\pi^{U}}(Z_{\tau_{2}}=k) = \mathbb{E}[ \mathbb{P}_{\pi^{U}}(Z_{\tau_{2}}=k | U_{2})]$
. Next, we notice that
Now, using that the event
![]() $\{\tau_{2}=n\}$
is same as
$\{\tau_{2}=n\}$
is same as
the right-hand side of the above inequality is bounded above by
 \begin{align*} \max_{i=0,1,\dots,U_{2}-1} \sum_{n=3}^{\infty} &\mathbb{P}\big(Z_{n}=k | Z_{n} \geq U_{2}, U_{2}, Z_{n-1}=i, \cap_{k=\nu_{1}+1}^{n-2} \{Z_{k}<U_{2}\}, \nu_{1} \leq n-1\big) \\[5pt] \times \ &\mathbb{P}_{\pi^{U}}(\tau_{2}=n | U_{2}).\end{align*}
\begin{align*} \max_{i=0,1,\dots,U_{2}-1} \sum_{n=3}^{\infty} &\mathbb{P}\big(Z_{n}=k | Z_{n} \geq U_{2}, U_{2}, Z_{n-1}=i, \cap_{k=\nu_{1}+1}^{n-2} \{Z_{k}<U_{2}\}, \nu_{1} \leq n-1\big) \\[5pt] \times \ &\mathbb{P}_{\pi^{U}}(\tau_{2}=n | U_{2}).\end{align*}
Since BPRE is a time-homogeneous Markov chain, it follows that
 \begin{align*} &\mathbb{P}\big(Z_{n}=k | Z_{n} \geq U_{2}, U_{2}, Z_{n-1}=i, \cap_{k=\nu_{1}+1}^{n-2} \{Z_{k}<U_{2}\}, \nu_{1} \leq n-1\big) \\[5pt] = \ &\mathbb{P}_{\delta_{i}^{L}}(Z_{1}=k | Z_{1} \geq U_{2}, U_{2}),\end{align*}
\begin{align*} &\mathbb{P}\big(Z_{n}=k | Z_{n} \geq U_{2}, U_{2}, Z_{n-1}=i, \cap_{k=\nu_{1}+1}^{n-2} \{Z_{k}<U_{2}\}, \nu_{1} \leq n-1\big) \\[5pt] = \ &\mathbb{P}_{\delta_{i}^{L}}(Z_{1}=k | Z_{1} \geq U_{2}, U_{2}),\end{align*}
where we also use the fact that the process starts in the supercritical regime. Now, using the fact that
![]() $U_{1}$
and
$U_{1}$
and
![]() $U_{2}$
are i.i.d., it follows that
$U_{2}$
are i.i.d., it follows that
Since
using the Fubini–Tonelli theorem, we obtain that
Now, for all
![]() $i=0,1,\dots,U_{1}-1$
, we have that
$i=0,1,\dots,U_{1}-1$
, we have that
Finally, using the assumptions ( H2 ), ( H3 ), and ( H9 ), we conclude that
A.4. Proofs of Lemma 4.1 and Lemma 4.2
Proof of Lemma
4.1. We begin by proving (i). It is sufficient to show that for
![]() $n \in \mathbb{N}_{0}$
and
$n \in \mathbb{N}_{0}$
and
![]() $k \in \mathbb{N}$
,
$k \in \mathbb{N}$
,
where
![]() $\boldsymbol{d}^{L}=\big(d_{1}^{L},\dots,d_{k}^{L}\big)$
,
$\boldsymbol{d}^{L}=\big(d_{1}^{L},\dots,d_{k}^{L}\big)$
,
![]() $\boldsymbol{d}^{U}=\big(d_{1}^{U},\dots,d_{k}^{U}\big)$
,
$\boldsymbol{d}^{U}=\big(d_{1}^{U},\dots,d_{k}^{U}\big)$
,
![]() $d_{j}^{L},d_{j}^{U} \in \mathbb{N}$
, and
$d_{j}^{L},d_{j}^{U} \in \mathbb{N}$
, and
![]() $\boldsymbol{B}_{i,n}^{L} \;:\!=\; \big\{ B_{i,l}^{L}\big\}_{l=1}^{n}$
. For simplicity set
$\boldsymbol{B}_{i,n}^{L} \;:\!=\; \big\{ B_{i,l}^{L}\big\}_{l=1}^{n}$
. For simplicity set
![]() $X_{j} \;:\!=\; Z_{\nu_{j}}$
. We recall that
$X_{j} \;:\!=\; Z_{\nu_{j}}$
. We recall that
![]() $\overline{\Delta}_{j}^{U}=\Delta_{j}^{U}+\Delta_{j}^{L}$
and notice
$\overline{\Delta}_{j}^{U}=\Delta_{j}^{U}+\Delta_{j}^{L}$
and notice
 \begin{align*} &\mathbb{P}_{\delta_{i}^{L}}\big( B_{i,n+1}^{L}=\big(k, \boldsymbol{d}^{L}, \boldsymbol{d}^{L}+\boldsymbol{d}^{U}\big) | \boldsymbol{B}_{i,n}^{L}\big)= \\[5pt] &\mathbb{P}_{\delta_{i}^{L}}\big( K_{i,n+1}^{L}=k, \cap_{j=1}^{k} \big\{\Delta_{T_{i,n}+j}^{U}=d_{j}^{U}, \Delta_{T_{i,n}+j}^{L}=d_{j}^{L}\big\} | X_{T_{i,n}^{L}} =i, \boldsymbol{B}_{i,n}^{L}\big)= \\[5pt] &\mathbb{P}_{\delta_{i}^{L}}\big( X_{T_{i,n}+k} =i, \cap_{j=1}^{k-1} \big\{X_{T_{i,n}+j} \neq i\big\}, \cap_{j=1}^{k} \big\{\Delta_{T_{i,n}+j}^{U} =d_{j}^{U}, \Delta_{T_{i,n}+j}^{L} =d_{j}^{L}\big\} | X_{T_{i,n}^{L}} =i, \boldsymbol{B}_{i,n}^{L}\big).\end{align*}
\begin{align*} &\mathbb{P}_{\delta_{i}^{L}}\big( B_{i,n+1}^{L}=\big(k, \boldsymbol{d}^{L}, \boldsymbol{d}^{L}+\boldsymbol{d}^{U}\big) | \boldsymbol{B}_{i,n}^{L}\big)= \\[5pt] &\mathbb{P}_{\delta_{i}^{L}}\big( K_{i,n+1}^{L}=k, \cap_{j=1}^{k} \big\{\Delta_{T_{i,n}+j}^{U}=d_{j}^{U}, \Delta_{T_{i,n}+j}^{L}=d_{j}^{L}\big\} | X_{T_{i,n}^{L}} =i, \boldsymbol{B}_{i,n}^{L}\big)= \\[5pt] &\mathbb{P}_{\delta_{i}^{L}}\big( X_{T_{i,n}+k} =i, \cap_{j=1}^{k-1} \big\{X_{T_{i,n}+j} \neq i\big\}, \cap_{j=1}^{k} \big\{\Delta_{T_{i,n}+j}^{U} =d_{j}^{U}, \Delta_{T_{i,n}+j}^{L} =d_{j}^{L}\big\} | X_{T_{i,n}^{L}} =i, \boldsymbol{B}_{i,n}^{L}\big).\end{align*}
We now compute the last term of the above equation. Specifically, by proceeding as in the proof of Lemma A.1 (involving conditioning on the environments), we obtain that for
![]() $n, k \in \mathbb{N}$
,
$n, k \in \mathbb{N}$
,
![]() $x_{j} \in S^{L}$
, and
$x_{j} \in S^{L}$
, and
![]() $x_{0}=i$
,
$x_{0}=i$
,
 \begin{align*} &\mathbb{P}_{\delta_{i}^{L}}\Big(\!\cap_{j=1}^{k} \Big\{X_{T_{i,n}^{L}+j}=x_{j}, \Delta_{T_{i,n}^{L}+j}^{U}=d_{j}^{U}, \Delta_{T_{i,n}^{L}+j}^{L}=d_{j}^{L}\Big\} | X_{T_{i,n}^{L}}=i, \boldsymbol{B}_{i,n}^{L}\Big) \\[5pt] =\ & \prod_{j=1}^{k} \mathbb{P}\Big(X_{T_{i,n}^{L}+j}=x_{j}, \Delta_{T_{i,n}^{L}+j}^{U}=d_{j}^{U}, \Delta_{T_{i,n}^{L}+j}^{L}=d_{j}^{L} | X_{T_{i,n}^{L}+j-1}=x_{j-1}\Big) \\[5pt] =\ &\prod_{j=1}^{k} \mathbb{P}\Big(X_{j}=x_{j}, \Delta_{j}^{U}=d_{j}^{U}, \Delta_{j}^{L}=d_{j}^{L} | X_{j-1}=x_{j-1}\Big) \\[5pt] =\ &\mathbb{P}\Big(\!\cap_{j=1}^{k} \Big\{X_{j}=x_{j}, \Delta_{j}^{U}=d_{j}^{U}, \Delta_{j}^{L}=d_{j}^{L}\Big\} | X_{0}=i\Big).\end{align*}
\begin{align*} &\mathbb{P}_{\delta_{i}^{L}}\Big(\!\cap_{j=1}^{k} \Big\{X_{T_{i,n}^{L}+j}=x_{j}, \Delta_{T_{i,n}^{L}+j}^{U}=d_{j}^{U}, \Delta_{T_{i,n}^{L}+j}^{L}=d_{j}^{L}\Big\} | X_{T_{i,n}^{L}}=i, \boldsymbol{B}_{i,n}^{L}\Big) \\[5pt] =\ & \prod_{j=1}^{k} \mathbb{P}\Big(X_{T_{i,n}^{L}+j}=x_{j}, \Delta_{T_{i,n}^{L}+j}^{U}=d_{j}^{U}, \Delta_{T_{i,n}^{L}+j}^{L}=d_{j}^{L} | X_{T_{i,n}^{L}+j-1}=x_{j-1}\Big) \\[5pt] =\ &\prod_{j=1}^{k} \mathbb{P}\Big(X_{j}=x_{j}, \Delta_{j}^{U}=d_{j}^{U}, \Delta_{j}^{L}=d_{j}^{L} | X_{j-1}=x_{j-1}\Big) \\[5pt] =\ &\mathbb{P}\Big(\!\cap_{j=1}^{k} \Big\{X_{j}=x_{j}, \Delta_{j}^{U}=d_{j}^{U}, \Delta_{j}^{L}=d_{j}^{L}\Big\} | X_{0}=i\Big).\end{align*}
Now, by summing over
![]() $x_{k} \in \{ i \}$
and
$x_{k} \in \{ i \}$
and
![]() $x_{j} \in S^{L} \setminus \{ i \}$
, we obtain that
$x_{j} \in S^{L} \setminus \{ i \}$
, we obtain that
 \begin{align*} &\mathbb{P}_{\delta_{i}^{L}}\big( X_{T_{i,n}+k}=i, \cap_{j=1}^{k-1} \big\{X_{T_{i,n}+j} \neq i\big\}, \cap_{j=1}^{k} \big\{\Delta_{T_{i,n}+j}^{U} =d_{j}^{U}, \Delta_{T_{i,n}+j}^{L}=d_{j}^{L}\big\} | X_{T_{i,n}^{L}}=i, \boldsymbol{B}_{i,n}^{L}\big) \\[5pt] =\ &\mathbb{P}_{\delta_{i}^{L}}\big(X_{k}=i, \cap_{j=1}^{k-1} \big\{X_{j} \neq i \big\}, \cap_{j=1}^{k} \big\{\Delta_{j}^{U}=d_{j}^{U}, \Delta_{j}^{L}=d_{j}^{L}\big\}\big).\end{align*}
\begin{align*} &\mathbb{P}_{\delta_{i}^{L}}\big( X_{T_{i,n}+k}=i, \cap_{j=1}^{k-1} \big\{X_{T_{i,n}+j} \neq i\big\}, \cap_{j=1}^{k} \big\{\Delta_{T_{i,n}+j}^{U} =d_{j}^{U}, \Delta_{T_{i,n}+j}^{L}=d_{j}^{L}\big\} | X_{T_{i,n}^{L}}=i, \boldsymbol{B}_{i,n}^{L}\big) \\[5pt] =\ &\mathbb{P}_{\delta_{i}^{L}}\big(X_{k}=i, \cap_{j=1}^{k-1} \big\{X_{j} \neq i \big\}, \cap_{j=1}^{k} \big\{\Delta_{j}^{U}=d_{j}^{U}, \Delta_{j}^{L}=d_{j}^{L}\big\}\big).\end{align*}
The last term in the above is
We thus obtain (27). The proof of (ii) is similar.
Proof of Lemma
4.2. The first part of (i) follows from Proposition 1.69 of Serfozo [Reference Serfozo27] with
![]() $X_{j}=Z_{\nu_{j}}$
,
$X_{j}=Z_{\nu_{j}}$
,
![]() $\pi=\pi^{L}=\{ \pi_{i}^{L} \}_{i \in S^{L}}$
, and
$\pi=\pi^{L}=\{ \pi_{i}^{L} \}_{i \in S^{L}}$
, and
![]() $V_{j}=\Delta_{j+1}^{U}$
. For the second part of (i) we use the above proposition with
$V_{j}=\Delta_{j+1}^{U}$
. For the second part of (i) we use the above proposition with
![]() $V_{j}=\overline{\Delta}_{j+1}^{U}$
and obtain that
$V_{j}=\overline{\Delta}_{j+1}^{U}$
and obtain that
Remark (3.2) yields that
We now prove the first part of (ii). Since, conditionally on
![]() $Z_{\nu_{0}}=i$
,
$Z_{\nu_{0}}=i$
,
![]() $\Delta_{1}^{U}$
and
$\Delta_{1}^{U}$
and
![]() $\Delta_{T_{i,1}^{L}+1}^{U}$
have the same distribution, using (i) we have that
$\Delta_{T_{i,1}^{L}+1}^{U}$
have the same distribution, using (i) we have that
 \begin{equation*} \mathbb{V}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U}\Big] =\mathbb{E}_{\delta_{i}^{L}} \left[ \left( \sum_{j=1}^{T_{i,1}^{L}}\big(\Delta_{j+1}^{U}-\mu^{U} \big)\right)^{2} \right] =\mathbb{E}_{\delta_{i}^{L}} \left[\sum_{j=1}^{T_{i,1}^{L}}\big(\Delta_{j+1}^{U}-\mu^{U}\big)^{2} \right] + 2 C_{i}^{U},\end{equation*}
\begin{equation*} \mathbb{V}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U}\Big] =\mathbb{E}_{\delta_{i}^{L}} \left[ \left( \sum_{j=1}^{T_{i,1}^{L}}\big(\Delta_{j+1}^{U}-\mu^{U} \big)\right)^{2} \right] =\mathbb{E}_{\delta_{i}^{L}} \left[\sum_{j=1}^{T_{i,1}^{L}}\big(\Delta_{j+1}^{U}-\mu^{U}\big)^{2} \right] + 2 C_{i}^{U},\end{equation*}
where
 \begin{equation*}C_{i}^{U} \;:\!=\; \mathbb{E}_{\delta_{i}^{L}} \left[\sum_{j=1}^{T_{i,1}^{L}}\big(\Delta_{j+1}^{U}-\mu^{U}\big) \sum_{l=j+1}^{T_{i,1}^{L}}\big(\Delta_{l+1}^{U}-\mu^{U}\big) \right].\end{equation*}
\begin{equation*}C_{i}^{U} \;:\!=\; \mathbb{E}_{\delta_{i}^{L}} \left[\sum_{j=1}^{T_{i,1}^{L}}\big(\Delta_{j+1}^{U}-\mu^{U}\big) \sum_{l=j+1}^{T_{i,1}^{L}}\big(\Delta_{l+1}^{U}-\mu^{U}\big) \right].\end{equation*}
Next, we apply Proposition 1.69 of Serfozo [Reference Serfozo27] with
![]() $X_{j}=Z_{\nu_{j}}$
,
$X_{j}=Z_{\nu_{j}}$
,
![]() $\pi=\pi^{L}=\{ \pi_{i}^{L} \}_{i \in S^{L}}$
, and
$\pi=\pi^{L}=\{ \pi_{i}^{L} \}_{i \in S^{L}}$
, and
![]() $V_{j}=\big(\Delta_{j+1}^{U}-\mu^{U}\big)^{2}$
and obtain that
$V_{j}=\big(\Delta_{j+1}^{U}-\mu^{U}\big)^{2}$
and obtain that
 \begin{equation*} \mathbb{E}_{\delta_{i}^{L}} \left[\sum_{j=1}^{T_{i,1}^{L}}\big(\Delta_{j+1}^{U}-\mu^{U}\big)^{2} \right] = \big(\pi_{i}^{L}\big)^{-1} \mathbb{E}_{\pi^{L}}\big[ \big(\Delta_{1}^{U}-\mu^{U}\big)^{2}\big].\end{equation*}
\begin{equation*} \mathbb{E}_{\delta_{i}^{L}} \left[\sum_{j=1}^{T_{i,1}^{L}}\big(\Delta_{j+1}^{U}-\mu^{U}\big)^{2} \right] = \big(\pi_{i}^{L}\big)^{-1} \mathbb{E}_{\pi^{L}}\big[ \big(\Delta_{1}^{U}-\mu^{U}\big)^{2}\big].\end{equation*}
Then we compute
 \begin{align*} C_{i}^{U}&= \mathbb{E}_{\delta_{i}^{L}}\Bigg[\sum_{j=1}^{\infty} \textbf{I}_{\{T_{i,1}^{L} \geq j\}} \mathbb{E}_{\delta_{i}^{L}} \Bigg[\big(\Delta_{j+1}^{U}-\mu^{U}\big) \sum_{l=j+1}^{T_{i,1}^{L}}\big(\Delta_{l+1}^{U}-\mu^{U}\big) | T_{i,1}^{L} \geq j \Bigg] \Bigg] \\[5pt] &= \mathbb{E}_{\delta_{i}^{L}} \Bigg[\sum_{j=1}^{\infty} \textbf{I}_{\{T_{i,1}^{L} \geq j\}} \sum_{k \in S^{L}} \textbf{I}_{\{Z_{\nu_{j}}=k\}} g^{L}(k) \Bigg] \\[5pt] &= \sum_{k \in S^{L}} g^{L}(k) \mathbb{E}_{\delta_{i}^{L}} \left[\sum_{j=1}^{T_{i,1}^{L}} \textbf{I}_{\{Z_{\nu_{j}}=k\}} \right],\end{align*}
\begin{align*} C_{i}^{U}&= \mathbb{E}_{\delta_{i}^{L}}\Bigg[\sum_{j=1}^{\infty} \textbf{I}_{\{T_{i,1}^{L} \geq j\}} \mathbb{E}_{\delta_{i}^{L}} \Bigg[\big(\Delta_{j+1}^{U}-\mu^{U}\big) \sum_{l=j+1}^{T_{i,1}^{L}}\big(\Delta_{l+1}^{U}-\mu^{U}\big) | T_{i,1}^{L} \geq j \Bigg] \Bigg] \\[5pt] &= \mathbb{E}_{\delta_{i}^{L}} \Bigg[\sum_{j=1}^{\infty} \textbf{I}_{\{T_{i,1}^{L} \geq j\}} \sum_{k \in S^{L}} \textbf{I}_{\{Z_{\nu_{j}}=k\}} g^{L}(k) \Bigg] \\[5pt] &= \sum_{k \in S^{L}} g^{L}(k) \mathbb{E}_{\delta_{i}^{L}} \left[\sum_{j=1}^{T_{i,1}^{L}} \textbf{I}_{\{Z_{\nu_{j}}=k\}} \right],\end{align*}
where
![]() $g^{L} \;:\; S^{L} \to \mathbb{R}$
is given by
$g^{L} \;:\; S^{L} \to \mathbb{R}$
is given by
 \begin{align*} g^{L}(k) &= \mathbb{E}_{\delta_{i}^{L}} \left[\big(\Delta_{j+1}^{U}-\mu^{U}\big) \sum_{l=j+1}^{T_{i,1}^{L}}\big(\Delta_{l+1}^{U}-\mu^{U}\big) | T_{i,1}^{L} \geq j, Z_{\nu_{j}}=k \right] \\[5pt] &= \sum_{l=j+1}^{\infty} \mathbb{E}_{\delta_{i}^{L}} \Big[\big(\Delta_{j+1}^{U}-\mu^{U}\big) \big(\Delta_{l+1}^{U}-\mu^{U}\big) \textbf{I}_{\{T_{i,1}^{L} \geq l\}} | T_{i,1}^{L} \geq j, Z_{\nu_{j}}=k \Big].\end{align*}
\begin{align*} g^{L}(k) &= \mathbb{E}_{\delta_{i}^{L}} \left[\big(\Delta_{j+1}^{U}-\mu^{U}\big) \sum_{l=j+1}^{T_{i,1}^{L}}\big(\Delta_{l+1}^{U}-\mu^{U}\big) | T_{i,1}^{L} \geq j, Z_{\nu_{j}}=k \right] \\[5pt] &= \sum_{l=j+1}^{\infty} \mathbb{E}_{\delta_{i}^{L}} \Big[\big(\Delta_{j+1}^{U}-\mu^{U}\big) \big(\Delta_{l+1}^{U}-\mu^{U}\big) \textbf{I}_{\{T_{i,1}^{L} \geq l\}} | T_{i,1}^{L} \geq j, Z_{\nu_{j}}=k \Big].\end{align*}
Using Theorem 1.54 of Serfozo [Reference Serfozo27], we obtain
 \begin{align*}\mathbb{E}_{\delta_{i}^{L}} \left[\sum_{j=1}^{T_{i,1}^{L}} \textbf{I}_{\{Z_{\nu_{j}}=k\}} \right] = \big(\pi_{i}^{L}\big)^{-1} \pi_{k}^{L},\end{align*}
\begin{align*}\mathbb{E}_{\delta_{i}^{L}} \left[\sum_{j=1}^{T_{i,1}^{L}} \textbf{I}_{\{Z_{\nu_{j}}=k\}} \right] = \big(\pi_{i}^{L}\big)^{-1} \pi_{k}^{L},\end{align*}
which yields
Now, using Lemma 4.1, we see that, conditionally on
![]() $j \leq T_{i,1}^{L} < l$
,
$j \leq T_{i,1}^{L} < l$
,
![]() $\big(\Delta_{l+1}^{U}-\mu^{U}\big)$
is independent of
$\big(\Delta_{l+1}^{U}-\mu^{U}\big)$
is independent of
![]() $\big(\Delta_{j+1}^{U}-\mu^{U}\big)$
. If
$\big(\Delta_{j+1}^{U}-\mu^{U}\big)$
. If
![]() $Z_{\nu_{j}} \sim \pi^{L}$
, then using stationarity (see Remark 3.1),
$Z_{\nu_{j}} \sim \pi^{L}$
, then using stationarity (see Remark 3.1),
Therefore,
 \begin{align*} &\sum_{l=j+1}^{\infty}\sum_{k \in S^{L}} \pi_{k}^{L} \mathbb{E}_{\delta_{i}^{L}} \Big[\big(\Delta_{j+1}^{U}-\mu^{U}\big) \big(\Delta_{l+1}^{U}-\mu^{U}\big) \textbf{I}_{\{T_{i,1}^{L}<l\}} | T_{i,1}^{L} \geq j, Z_{\nu_{j}}=k \Big]= \\[5pt] &\sum_{l=j+1}^{\infty} \mathbb{E}_{\delta_{i}^{L}} \Big[\big(\Delta_{j+1}^{U} -\mu^{U}\big) \mathbb{E}\big[\big(\Delta_{l+1}^{U} -\mu^{U}\big) | j \leq T_{i,1}^{L}<l,Z_{\nu_{j}} \sim \pi^{L}\big] \textbf{I}_{\{T_{i,1}^{L}<l\}} | T_{i,1}^{L} \geq j, Z_{\nu_{j}} \sim \pi^{L} \Big]\end{align*}
\begin{align*} &\sum_{l=j+1}^{\infty}\sum_{k \in S^{L}} \pi_{k}^{L} \mathbb{E}_{\delta_{i}^{L}} \Big[\big(\Delta_{j+1}^{U}-\mu^{U}\big) \big(\Delta_{l+1}^{U}-\mu^{U}\big) \textbf{I}_{\{T_{i,1}^{L}<l\}} | T_{i,1}^{L} \geq j, Z_{\nu_{j}}=k \Big]= \\[5pt] &\sum_{l=j+1}^{\infty} \mathbb{E}_{\delta_{i}^{L}} \Big[\big(\Delta_{j+1}^{U} -\mu^{U}\big) \mathbb{E}\big[\big(\Delta_{l+1}^{U} -\mu^{U}\big) | j \leq T_{i,1}^{L}<l,Z_{\nu_{j}} \sim \pi^{L}\big] \textbf{I}_{\{T_{i,1}^{L}<l\}} | T_{i,1}^{L} \geq j, Z_{\nu_{j}} \sim \pi^{L} \Big]\end{align*}
equals 0. Adding the above to
![]() $\sum_{k \in S^{L}} g^{L}(k) \pi_{k}^{L}$
, we conclude that
$\sum_{k \in S^{L}} g^{L}(k) \pi_{k}^{L}$
, we conclude that
 \begin{align*} \sum_{k \in S^{L}} g^{L}(k) \pi_{k}^{L} &= \sum_{l=j+1}^{\infty} \sum_{k \in S^{L}} \pi_{k}^{L} \mathbb{E}_{\delta_{i}^{L}} \Big[\big(\Delta_{j+1}^{U}-\mu^{U}\big) \big(\Delta_{l+1}^{U}-\mu^{U}\big) | T_{i,1}^{L} \geq j, Z_{\nu_{j}}=k\Big] \\[5pt] = &\sum_{l=1}^{\infty} \sum_{k \in S^{L}} \pi_{k}^{L} \mathbb{E}_{\delta_{k}^{L}} \Big[\big(\Delta_{1}^{U}-\mu^{U}\big) \big(\Delta_{l+1}^{U}-\mu^{U}\big) \Big] \\[5pt] &=\sum_{l=1}^{\infty} \mathbb{C}_{\pi^{L}}\big[\Delta_{1}^{U}, \Delta_{l+1}^{U}\big].\end{align*}
\begin{align*} \sum_{k \in S^{L}} g^{L}(k) \pi_{k}^{L} &= \sum_{l=j+1}^{\infty} \sum_{k \in S^{L}} \pi_{k}^{L} \mathbb{E}_{\delta_{i}^{L}} \Big[\big(\Delta_{j+1}^{U}-\mu^{U}\big) \big(\Delta_{l+1}^{U}-\mu^{U}\big) | T_{i,1}^{L} \geq j, Z_{\nu_{j}}=k\Big] \\[5pt] = &\sum_{l=1}^{\infty} \sum_{k \in S^{L}} \pi_{k}^{L} \mathbb{E}_{\delta_{k}^{L}} \Big[\big(\Delta_{1}^{U}-\mu^{U}\big) \big(\Delta_{l+1}^{U}-\mu^{U}\big) \Big] \\[5pt] &=\sum_{l=1}^{\infty} \mathbb{C}_{\pi^{L}}\big[\Delta_{1}^{U}, \Delta_{l+1}^{U}\big].\end{align*}
The second part of (ii) and (iii) are obtained similarly.
A.5. Finiteness of
 $\mu^{\boldsymbol{T}}$
,
$\mu^{\boldsymbol{T}}$
,
 $\sigma^{2,\boldsymbol{T}}$
, and
$\sigma^{2,\boldsymbol{T}}$
, and
 $\overline{\sigma}^{2,\boldsymbol{T}}$
$\overline{\sigma}^{2,\boldsymbol{T}}$
We establish positivity and finiteness of
![]() $\sigma^{2,T}$
and
$\sigma^{2,T}$
and
![]() $\overline{\sigma}^{2,T}$
, where
$\overline{\sigma}^{2,T}$
, where
![]() $T \in \{L,U\}$
. Lemma A.2 below is used to control the covariance terms in
$T \in \{L,U\}$
. Lemma A.2 below is used to control the covariance terms in
![]() $\sigma^{2,T}$
and
$\sigma^{2,T}$
and
![]() $\overline{\sigma}^{2,T}$
. We recall that uniform ergodicity of the Markov chains
$\overline{\sigma}^{2,T}$
. We recall that uniform ergodicity of the Markov chains
![]() $\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
$\big\{ Z_{\nu_{j}} \big\}_{j=0}^{\infty}$
and
![]() $\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
is equivalent to the existence of constants
$\big\{ Z_{\tau_{j}} \big\}_{j=1}^{\infty}$
is equivalent to the existence of constants
![]() $C_{T} \geq 0$
and
$C_{T} \geq 0$
and
![]() $\rho_{T} \in (0,1)$
such that
$\rho_{T} \in (0,1)$
such that
![]() $\sup_{l \in S_{T}} \lVert p_{l}^{T}(j)- \pi^{T}\rVert \leq C_{T} \rho_{T}^{j}$
.
$\sup_{l \in S_{T}} \lVert p_{l}^{T}(j)- \pi^{T}\rVert \leq C_{T} \rho_{T}^{j}$
.
Lemma A.2. Assume ( H1 )–( H4 ).The following holds:
-
(i) If ( H5 ) holds and
 $w_{i} \in \mathbb{R}$
,
$w_{i} \in \mathbb{R}$
,
 $i \in S^{L}$
, then
$i \in S^{L}$
, then  \begin{equation*} \sum_{j=1}^{\infty} \biggl\lvert \sum_{i,k \in S^{L}} w_{k} w_{i} \pi_{k}^{L} p_{ki}^{L}(j) - \!\left( \sum_{k \in S^{L}} w_{k} \pi_{k}^{L} \!\right) \!\left( \sum_{i \in S^{L}} w_{i} \pi_{i}^{L} \!\right) \biggr\rvert \leq 2 C_{L}^{1/2} \frac{\rho_{L}^{1/2}}{1-\rho_{L}^{1/2}} \!\left( \sum_{k \in S^{L}} w_{k}^{2} \pi_{k}^{L} \!\right)\!.\end{equation*}
\begin{equation*} \sum_{j=1}^{\infty} \biggl\lvert \sum_{i,k \in S^{L}} w_{k} w_{i} \pi_{k}^{L} p_{ki}^{L}(j) - \!\left( \sum_{k \in S^{L}} w_{k} \pi_{k}^{L} \!\right) \!\left( \sum_{i \in S^{L}} w_{i} \pi_{i}^{L} \!\right) \biggr\rvert \leq 2 C_{L}^{1/2} \frac{\rho_{L}^{1/2}}{1-\rho_{L}^{1/2}} \!\left( \sum_{k \in S^{L}} w_{k}^{2} \pi_{k}^{L} \!\right)\!.\end{equation*}
-
(ii) If ( H6 ) (or ( H7 ))holds and
 $w_{k} \in \mathbb{R}$
,
$w_{k} \in \mathbb{R}$
,
 $k \in S^{U}$
, then
$k \in S^{U}$
, then  \begin{equation*} \sum_{j=1}^{\infty} \biggl\lvert \sum_{i,k \in S^{U}} w_{k} w_{i} \pi_{k}^{U} p_{ki}^{U}(j) - \!\left( \sum_{k \in S^{U}} w_{k} \pi_{k}^{U} \!\right) \!\left( \sum_{i \in S^{U}} w_{i} \pi_{i}^{U} \!\right) \biggr\rvert \leq 2 C_{U}^{1/2} \frac{\rho_{U}^{1/2}}{1-\rho_{U}^{1/2}} \!\left( \sum_{k \in S^{U}} w_{k}^{2} \pi_{k}^{U} \!\right)\!.\end{equation*}
\begin{equation*} \sum_{j=1}^{\infty} \biggl\lvert \sum_{i,k \in S^{U}} w_{k} w_{i} \pi_{k}^{U} p_{ki}^{U}(j) - \!\left( \sum_{k \in S^{U}} w_{k} \pi_{k}^{U} \!\right) \!\left( \sum_{i \in S^{U}} w_{i} \pi_{i}^{U} \!\right) \biggr\rvert \leq 2 C_{U}^{1/2} \frac{\rho_{U}^{1/2}}{1-\rho_{U}^{1/2}} \!\left( \sum_{k \in S^{U}} w_{k}^{2} \pi_{k}^{U} \!\right)\!.\end{equation*}
The proof of the above lemma can be constructed along the lines of Theorem 17.2.3 of Ibragimov and Linnik [Reference Ibragimov and Linnik31] with
![]() $p=q=1/2$
; it involves repeated use of the Cauchy–Schwarz inequality and the stationarity in Remark 3.1.
$p=q=1/2$
; it involves repeated use of the Cauchy–Schwarz inequality and the stationarity in Remark 3.1.
Proof of Lemma A.2. Since the proof of (ii) is similar, we only prove (i). We proceed along the lines of the proof of Theorem 17.2.3 of Ibragimov and Linnik [Reference Ibragimov and Linnik31]. Using the Cauchy–Schwarz inequality, we have that
 \begin{align*} &\biggl\lvert \sum_{i,k \in S^{L}} w_{k} w_{i} \pi_{k}^{L} p_{ki}^{L}(j) - \left( \sum_{k \in S^{L}} w_{k} \pi_{k}^{L} \right) \left( \sum_{i \in S^{L}} w_{i} \pi_{i}^{L} \right) \biggr\rvert \\[5pt] =\ &\biggl\lvert \sum_{k \in S^{L}} w_{k} \big(\pi_{k}^{L}\big)^{1/2} \sum_{i \in S^{L}} w_{i} \big(p_{ki}^{L}(j)-\pi_{i}^{L}\big) \big(\pi_{k}^{L}\big)^{1/2} \biggr\rvert \\[5pt] \leq\ & \left( \sum_{k \in S^{L}} (w_{k})^{2} \pi_{k}^{L} \right)^{1/2} \left( \sum_{k \in S^{L}} \pi_{k}^{L} \left( \sum_{i \in S^{L}} w_{i} \big(p_{ki}^{L}(j)-\pi_{i}^{L}\big) \right)^{2} \right)^{1/2}.\end{align*}
\begin{align*} &\biggl\lvert \sum_{i,k \in S^{L}} w_{k} w_{i} \pi_{k}^{L} p_{ki}^{L}(j) - \left( \sum_{k \in S^{L}} w_{k} \pi_{k}^{L} \right) \left( \sum_{i \in S^{L}} w_{i} \pi_{i}^{L} \right) \biggr\rvert \\[5pt] =\ &\biggl\lvert \sum_{k \in S^{L}} w_{k} \big(\pi_{k}^{L}\big)^{1/2} \sum_{i \in S^{L}} w_{i} \big(p_{ki}^{L}(j)-\pi_{i}^{L}\big) \big(\pi_{k}^{L}\big)^{1/2} \biggr\rvert \\[5pt] \leq\ & \left( \sum_{k \in S^{L}} (w_{k})^{2} \pi_{k}^{L} \right)^{1/2} \left( \sum_{k \in S^{L}} \pi_{k}^{L} \left( \sum_{i \in S^{L}} w_{i} \big(p_{ki}^{L}(j)-\pi_{i}^{L}\big) \right)^{2} \right)^{1/2}.\end{align*}
Using the Cauchy–Schwarz inequality again, we obtain that
 \begin{align*} \Bigg( \sum_{i \in S^{L}} w_{i} \big(p_{ki}^{L}(j)-\pi_{i}^{L}\big) \Bigg)^{2} &\leq \Bigg( \sum_{i \in S^{L}} \lvert w_{i}\rvert \big(p_{ki}^{L}(j)+\pi_{i}^{L}\big)^{1/2} \lvert p_{ki}^{L}(j)-\pi_{i}^{L}\rvert^{1/2} \Bigg)^{2} \\[5pt] &\leq \Bigg( \sum_{i \in S^{L}} (w_{i})^{2} \big(p_{ki}^{L}(j)+\pi_{i}^{L}\big) \Bigg) \Bigg( \sum_{i \in S^{L}} \lvert p_{ki}^{L}(j)-\pi_{i}^{L}\rvert \Bigg).\end{align*}
\begin{align*} \Bigg( \sum_{i \in S^{L}} w_{i} \big(p_{ki}^{L}(j)-\pi_{i}^{L}\big) \Bigg)^{2} &\leq \Bigg( \sum_{i \in S^{L}} \lvert w_{i}\rvert \big(p_{ki}^{L}(j)+\pi_{i}^{L}\big)^{1/2} \lvert p_{ki}^{L}(j)-\pi_{i}^{L}\rvert^{1/2} \Bigg)^{2} \\[5pt] &\leq \Bigg( \sum_{i \in S^{L}} (w_{i})^{2} \big(p_{ki}^{L}(j)+\pi_{i}^{L}\big) \Bigg) \Bigg( \sum_{i \in S^{L}} \lvert p_{ki}^{L}(j)-\pi_{i}^{L}\rvert \Bigg).\end{align*}
Since
![]() $\sum_{k \in S^{L}} p_{ki}^{L}(j) \pi_{k}^{L}=\pi_{i}^{L}$
by Remark 3.1, we deduce that
$\sum_{k \in S^{L}} p_{ki}^{L}(j) \pi_{k}^{L}=\pi_{i}^{L}$
by Remark 3.1, we deduce that
 \begin{align*} &\Bigg( \sum_{k \in S^{L}} \pi_{k}^{L} \Bigg( \sum_{i \in S^{L}} w_{i} \big(p_{ki}^{L}(j)-\pi_{i}^{L}\big) \Bigg)^{2} \Bigg)^{1/2} \\[5pt] \leq& \Bigg( \sum_{k \in S^{L}} \pi_{k}^{L} \Bigg( \sum_{i \in S^{L}} (w_{i})^{2} \big(p_{ki}^{L}(j)+\pi_{i}^{L}\big) \Bigg) \Bigg( \sum_{i \in S^{L}} \lvert p_{ki}^{L}(j)-\pi_{i}^{L}\rvert \Bigg) \Bigg)^{1/2} \\[5pt] \leq &\Bigg( 2 \sum_{i \in S^{L}} (w_{i})^{2} \pi_{i}^{L} \Bigg)^{1/2} \sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L}} \lvert p_{ki}^{L}(j)-\pi_{i}^{L}\rvert \Bigg)^{1/2}.\end{align*}
\begin{align*} &\Bigg( \sum_{k \in S^{L}} \pi_{k}^{L} \Bigg( \sum_{i \in S^{L}} w_{i} \big(p_{ki}^{L}(j)-\pi_{i}^{L}\big) \Bigg)^{2} \Bigg)^{1/2} \\[5pt] \leq& \Bigg( \sum_{k \in S^{L}} \pi_{k}^{L} \Bigg( \sum_{i \in S^{L}} (w_{i})^{2} \big(p_{ki}^{L}(j)+\pi_{i}^{L}\big) \Bigg) \Bigg( \sum_{i \in S^{L}} \lvert p_{ki}^{L}(j)-\pi_{i}^{L}\rvert \Bigg) \Bigg)^{1/2} \\[5pt] \leq &\Bigg( 2 \sum_{i \in S^{L}} (w_{i})^{2} \pi_{i}^{L} \Bigg)^{1/2} \sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L}} \lvert p_{ki}^{L}(j)-\pi_{i}^{L}\rvert \Bigg)^{1/2}.\end{align*}
Using that
![]() $\sup_{l \in S^{L}} \lVert p_{l}^{L}(j)- \pi^{L}\rVert \leq C_{L} \rho_{L}^{j}$
, we obtain that
$\sup_{l \in S^{L}} \lVert p_{l}^{L}(j)- \pi^{L}\rVert \leq C_{L} \rho_{L}^{j}$
, we obtain that
 \begin{align*} &\sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L}} \lvert p_{ki}^{L}(j)-\pi_{i}^{L}\rvert \Bigg) \\[5pt] \leq& \sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L} > 0} \big(p_{ki}^{L}(j)-\pi_{i}^{L}\big) \Bigg) + \sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L}< 0} \big(\pi_{i}^{L}-p_{ki}^{L}(j)\big) \Bigg) \\[5pt] \leq& \sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L} > 0} p_{ki}^{L}(j) - \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L} > 0} \pi_{i}^{L} \Bigg) \\[5pt] +& \sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L} < 0} \pi_{i}^{L}- \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L}< 0} p_{ki}^{L}(j) \Bigg) \\[5pt] \leq& 2C_{L}\rho_{L}^{j}.\end{align*}
\begin{align*} &\sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L}} \lvert p_{ki}^{L}(j)-\pi_{i}^{L}\rvert \Bigg) \\[5pt] \leq& \sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L} > 0} \big(p_{ki}^{L}(j)-\pi_{i}^{L}\big) \Bigg) + \sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L}< 0} \big(\pi_{i}^{L}-p_{ki}^{L}(j)\big) \Bigg) \\[5pt] \leq& \sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L} > 0} p_{ki}^{L}(j) - \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L} > 0} \pi_{i}^{L} \Bigg) \\[5pt] +& \sup_{k \in S^{L}} \Bigg( \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L} < 0} \pi_{i}^{L}- \sum_{i \in S^{L} \;:\; p_{ki}^{L}(j)-\pi_{i}^{L}< 0} p_{ki}^{L}(j) \Bigg) \\[5pt] \leq& 2C_{L}\rho_{L}^{j}.\end{align*}
We have thus shown that
 \begin{equation*} \Bigg\lvert \sum_{i,k \in S^{L}} w_{k} w_{i} \pi_{k}^{L} p_{ki}^{L}(j) - \Bigg( \sum_{k \in S^{L}} w_{k} \pi_{k}^{L} \Bigg) \Bigg( \sum_{i \in S^{L}} w_{i} \pi_{i}^{L} \Bigg) \Bigg\rvert \leq 2 C_{L}^{1/2} \rho_{L}^{j/2} \Bigg( \sum_{k \in S^{L}} w_{k}^{2} \pi_{k}^{L} \Bigg),\end{equation*}
\begin{equation*} \Bigg\lvert \sum_{i,k \in S^{L}} w_{k} w_{i} \pi_{k}^{L} p_{ki}^{L}(j) - \Bigg( \sum_{k \in S^{L}} w_{k} \pi_{k}^{L} \Bigg) \Bigg( \sum_{i \in S^{L}} w_{i} \pi_{i}^{L} \Bigg) \Bigg\rvert \leq 2 C_{L}^{1/2} \rho_{L}^{j/2} \Bigg( \sum_{k \in S^{L}} w_{k}^{2} \pi_{k}^{L} \Bigg),\end{equation*}
which yields that
 \begin{equation*} \sum_{j=1}^{\infty} \Bigg\lvert \sum_{i,k \in S^{L}} w_{k} w_{i} \pi_{k}^{L} p_{ki}^{L}(j) - \Bigg( \sum_{k \in S^{L}} w_{k} \pi_{k}^{L} \Bigg) \Bigg( \sum_{i \in S^{L}} w_{i} \pi_{i}^{L} \Bigg) \Bigg\rvert \leq 2 C_{L}^{1/2} \frac{\rho_{L}^{1/2}}{1-\rho_{L}^{1/2}} \Bigg( \sum_{k \in S^{L}} w_{k}^{2} \pi_{k}^{L} \Bigg).\end{equation*}
\begin{equation*} \sum_{j=1}^{\infty} \Bigg\lvert \sum_{i,k \in S^{L}} w_{k} w_{i} \pi_{k}^{L} p_{ki}^{L}(j) - \Bigg( \sum_{k \in S^{L}} w_{k} \pi_{k}^{L} \Bigg) \Bigg( \sum_{i \in S^{L}} w_{i} \pi_{i}^{L} \Bigg) \Bigg\rvert \leq 2 C_{L}^{1/2} \frac{\rho_{L}^{1/2}}{1-\rho_{L}^{1/2}} \Bigg( \sum_{k \in S^{L}} w_{k}^{2} \pi_{k}^{L} \Bigg).\end{equation*}
We are now ready to study the finiteness of means and variances
![]() $\mu^{T}$
,
$\mu^{T}$
,
![]() $\sigma^{2,T}$
, and
$\sigma^{2,T}$
, and
![]() $\overline{\sigma}^{2,T}$
, where
$\overline{\sigma}^{2,T}$
, where
![]() $T \in \{L,U\}$
.
$T \in \{L,U\}$
.
Proposition A.2.
Assume (
H1
)–(
H4
). (i) If (
H5
) and (
H8
) also hold, then
![]() $\mu^{U}< \infty$
and
$\mu^{U}< \infty$
and
![]() $0<\sigma^{2,U}<\infty$
. (ii) Next, if (
H6
) (or (
H7
)) and (
H9
) hold, then
$0<\sigma^{2,U}<\infty$
. (ii) Next, if (
H6
) (or (
H7
)) and (
H9
) hold, then
![]() $\mu^{L}<\infty$
and
$\mu^{L}<\infty$
and
![]() $0<\sigma^{2,L}<\infty$
. (iii) Additionally, under the assumptions in (i) and (ii), we have
$0<\sigma^{2,L}<\infty$
. (iii) Additionally, under the assumptions in (i) and (ii), we have
![]() $0<\overline{\sigma}^{2,U},\overline{\sigma}^{2,L} <\infty$
.
$0<\overline{\sigma}^{2,U},\overline{\sigma}^{2,L} <\infty$
.
It is easy to see that Proposition A.2 implies that
![]() $\lvert\mathbb{C}^{U}\rvert$
and
$\lvert\mathbb{C}^{U}\rvert$
and
![]() $\lvert\mathbb{C}^{L}\rvert$
are finite.
$\lvert\mathbb{C}^{L}\rvert$
are finite.
Proof of Proposition
A.2. We begin by proving (i). For all
![]() $i \in S^{L}$
it holds that
$i \in S^{L}$
it holds that
where
![]() $\{ \tilde{Z}_{n} \}_{n=0}^{\infty}$
is a supercritical BPRE with immigration having environmental sequence
$\{ \tilde{Z}_{n} \}_{n=0}^{\infty}$
is a supercritical BPRE with immigration having environmental sequence
![]() $\Pi^{U} = \{ \Pi_{n}^{U} \}_{n=0}^{\infty}$
and, conditionally on
$\Pi^{U} = \{ \Pi_{n}^{U} \}_{n=0}^{\infty}$
and, conditionally on
![]() $\Pi_{n}^{U}$
, offspring distributions
$\Pi_{n}^{U}$
, offspring distributions
![]() $\{ \xi_{n,i}^{U} \}_{i=0}^{\infty}$
and immigration distribution
$\{ \xi_{n,i}^{U} \}_{i=0}^{\infty}$
and immigration distribution
![]() $I_{n}^{U}$
. Using the fact that
$I_{n}^{U}$
. Using the fact that
![]() $\lim_{n \to \infty} \tilde{Z}_{n}=\infty$
a.s. and
$\lim_{n \to \infty} \tilde{Z}_{n}=\infty$
a.s. and
![]() $\mathbb{E}[U_{1}]< \infty$
, we see that
$\mathbb{E}[U_{1}]< \infty$
, we see that
![]() $\lim_{n \to \infty} \tilde{Z}_{n} \mathbb{P}_{\delta_{i}^{L}}(\tilde{Z}_{n} < U_{1} | \tilde{Z}_{n})=0$
a.s. Since
$\lim_{n \to \infty} \tilde{Z}_{n} \mathbb{P}_{\delta_{i}^{L}}(\tilde{Z}_{n} < U_{1} | \tilde{Z}_{n})=0$
a.s. Since
![]() $\lim_{n \to \infty} \frac{\tilde{Z}_{n}}{(M^{L})^{n}}>0$
, we obtain
$\lim_{n \to \infty} \frac{\tilde{Z}_{n}}{(M^{L})^{n}}>0$
, we obtain
![]() $\lim_{n \to \infty} (M^{L})^{n} \mathbb{P}_{\delta_{i}^{L}}(\tilde{Z}_{n} < U_{1} | \tilde{Z}_{n})=0$
a.s., which yields
$\lim_{n \to \infty} (M^{L})^{n} \mathbb{P}_{\delta_{i}^{L}}(\tilde{Z}_{n} < U_{1} | \tilde{Z}_{n})=0$
a.s., which yields
![]() $\lim_{n \to \infty} (M^{L})^{n} \mathbb{P}_{\delta_{i}^{L}}(\tilde{Z}_{n} < U_{1})=0$
. Therefore, there exists
$\lim_{n \to \infty} (M^{L})^{n} \mathbb{P}_{\delta_{i}^{L}}(\tilde{Z}_{n} < U_{1})=0$
. Therefore, there exists
![]() $\tilde{C}$
such that
$\tilde{C}$
such that
Now, using the fact that
![]() $S^{L}$
is finite and
$S^{L}$
is finite and
![]() $\mathbb{E}[U_{1}]<\infty$
, it follows that
$\mathbb{E}[U_{1}]<\infty$
, it follows that
Turning to the finiteness of
![]() $\sigma^{2,U}$
, replacing n by
$\sigma^{2,U}$
, replacing n by
![]() $\lfloor \sqrt{n} \rfloor$
in (28), one obtains that
$\lfloor \sqrt{n} \rfloor$
in (28), one obtains that
This together with the finiteness of
![]() $\mu^{U}$
yields
$\mu^{U}$
yields
![]() $\mathbb{V}_{\pi^{L}}[ \Delta_{1}^{U}] < \infty$
. Turning to the covariance terms in
$\mathbb{V}_{\pi^{L}}[ \Delta_{1}^{U}] < \infty$
. Turning to the covariance terms in
![]() $\sigma^{2,U}$
, we apply Lemma A.2(i) with
$\sigma^{2,U}$
, we apply Lemma A.2(i) with
![]() $w_{i} = \mathbb{E}_{\delta_{i}^{L}}[\tau_{1} - \mu^{U}]$
, and using
$w_{i} = \mathbb{E}_{\delta_{i}^{L}}[\tau_{1} - \mu^{U}]$
, and using
![]() $\sum_{i \in S^{L}} w_{i} \pi_{i}^{L}=0$
, we obtain that
$\sum_{i \in S^{L}} w_{i} \pi_{i}^{L}=0$
, we obtain that
 \begin{align*} \sum_{j=1}^{\infty} \lvert\mathbb{C}_{\pi^{L}}\Big[ \Delta_{1}^{U}, \Delta_{j+1}^{U} \Big]\rvert &= \sum_{j=1}^{\infty} \lvert\sum_{k \in S^{L}} \mathbb{E}_{\delta_{k}^{L}}\Big[\tau_{1}-\mu^{U}\Big] \pi_{k}^{L} \sum_{i \in S^{L}} \mathbb{E}_{\delta_{i}^{L}}\Big[ \tau_{1}-\mu^{U}\Big] p_{ki}^{L}(j)\rvert \\[5pt] &\leq 2 C_{L}^{1/2} \biggl( \frac{\rho_{L}^{1/2}}{1-\rho_{L}^{1/2}} \biggr) \Bigg( \sum_{k \in S^{L}} \big( \mathbb{E}_{\delta_{k}^{L}}\big[\tau_{1}-\mu^{U}\big] \big)^{2} \pi_{k}^{L} \Bigg) < \infty.\end{align*}
\begin{align*} \sum_{j=1}^{\infty} \lvert\mathbb{C}_{\pi^{L}}\Big[ \Delta_{1}^{U}, \Delta_{j+1}^{U} \Big]\rvert &= \sum_{j=1}^{\infty} \lvert\sum_{k \in S^{L}} \mathbb{E}_{\delta_{k}^{L}}\Big[\tau_{1}-\mu^{U}\Big] \pi_{k}^{L} \sum_{i \in S^{L}} \mathbb{E}_{\delta_{i}^{L}}\Big[ \tau_{1}-\mu^{U}\Big] p_{ki}^{L}(j)\rvert \\[5pt] &\leq 2 C_{L}^{1/2} \biggl( \frac{\rho_{L}^{1/2}}{1-\rho_{L}^{1/2}} \biggr) \Bigg( \sum_{k \in S^{L}} \big( \mathbb{E}_{\delta_{k}^{L}}\big[\tau_{1}-\mu^{U}\big] \big)^{2} \pi_{k}^{L} \Bigg) < \infty.\end{align*}
We conclude that
![]() $\sigma^{2,U}$
is finite. For
$\sigma^{2,U}$
is finite. For
![]() $i \in S^{U}$
, it holds that
$i \in S^{U}$
, it holds that
where the inequality follows from the upper bound on the extinction time of the process in the subcritical regime. Hence, using Proposition A.1 it follows that
![]() $\mu^{L} \leq \frac{\overline{\pi}^{U}}{1-M^{L}} < \infty$
.
$\mu^{L} \leq \frac{\overline{\pi}^{U}}{1-M^{L}} < \infty$
.
Next we show that
![]() $\sigma^{2,L}$
is finite. As before, we obtain that for all
$\sigma^{2,L}$
is finite. As before, we obtain that for all
![]() $i \in S^{U}$
,
$i \in S^{U}$
,
yielding that
This together with the finiteness of
![]() $\mu^{L}<\infty$
implies that
$\mu^{L}<\infty$
implies that
![]() $\mathbb{V}_{\pi^{L}}\big[ \Delta_{1}^{L}\big]<\infty$
. Turning to covariances, we apply Lemma A.2(ii) with
$\mathbb{V}_{\pi^{L}}\big[ \Delta_{1}^{L}\big]<\infty$
. Turning to covariances, we apply Lemma A.2(ii) with
![]() $w_{i} = \mathbb{E}_{\delta_{i}^{U}}\big[\Delta_{1}^{L} - \mu^{L}\big]$
, and using the fact that
$w_{i} = \mathbb{E}_{\delta_{i}^{U}}\big[\Delta_{1}^{L} - \mu^{L}\big]$
, and using the fact that
![]() $\sum_{i \in S^{U}} w_{i} \pi_{i}^{U}=0$
, we obtain that
$\sum_{i \in S^{U}} w_{i} \pi_{i}^{U}=0$
, we obtain that
 \begin{equation*} \sum_{j=1}^{\infty} \lvert\mathbb{C}_{\pi^{U}}\big[ \Delta_{1}^{L}, \Delta_{j+1}^{L}\big]\rvert \leq 2 C_{U}^{1/2} \left( \frac{\rho_{U}^{1/2}}{1-\rho_{U}^{1/2}} \right) \left( \sum_{k \in S^{U}} \big(\mathbb{E}_{\delta_{k}^{U}}\big[\Delta_{1}^{L}-\mu^{L}\big] \big)^{2} \pi_{k}^{U} \right) < \infty,\end{equation*}
\begin{equation*} \sum_{j=1}^{\infty} \lvert\mathbb{C}_{\pi^{U}}\big[ \Delta_{1}^{L}, \Delta_{j+1}^{L}\big]\rvert \leq 2 C_{U}^{1/2} \left( \frac{\rho_{U}^{1/2}}{1-\rho_{U}^{1/2}} \right) \left( \sum_{k \in S^{U}} \big(\mathbb{E}_{\delta_{k}^{U}}\big[\Delta_{1}^{L}-\mu^{L}\big] \big)^{2} \pi_{k}^{U} \right) < \infty,\end{equation*}
yielding the finiteness of
![]() $\sigma^{2,L}$
. Turning to (iii), we compute
$\sigma^{2,L}$
. Turning to (iii), we compute
where, by Part (i),
![]() $\mathbb{V}_{\pi^{L}}\Big[ \Delta_{1}^{U} \Big] < \infty$
, and using Remark 3.2,
$\mathbb{V}_{\pi^{L}}\Big[ \Delta_{1}^{U} \Big] < \infty$
, and using Remark 3.2,
Turning to the covariance, we again apply Lemma A.2 (i) with
![]() $w_{i} = \mathbb{E}_{\delta_{i}^{L}}\left[\overline{\Delta}_{1}^{U} - \big(\mu^{U}+\mu^{L}\big)\right]$
and conclude that also
$w_{i} = \mathbb{E}_{\delta_{i}^{L}}\left[\overline{\Delta}_{1}^{U} - \big(\mu^{U}+\mu^{L}\big)\right]$
and conclude that also
 \begin{equation*} \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{L}}\Big[ \overline{\Delta}_{1}^{U}, \overline{\Delta}_{j+1}^{U}\Big] \leq 2 C_{L}^{1/2} \Bigg( \frac{\rho_{L}^{1/2}}{1-\rho_{L}^{1/2}} \Bigg) \Bigg( \sum_{k \in S^{L}} \Big( \mathbb{E}_{\delta_{k}^{L}}\Big[\overline{\Delta}_{1}^{U} - \big(\mu^{U}+\mu^{L}\big)\Big] \Big)^{2} \pi_{k}^{L} \Bigg).\end{equation*}
\begin{equation*} \sum_{j=1}^{\infty} \mathbb{C}_{\pi^{L}}\Big[ \overline{\Delta}_{1}^{U}, \overline{\Delta}_{j+1}^{U}\Big] \leq 2 C_{L}^{1/2} \Bigg( \frac{\rho_{L}^{1/2}}{1-\rho_{L}^{1/2}} \Bigg) \Bigg( \sum_{k \in S^{L}} \Big( \mathbb{E}_{\delta_{k}^{L}}\Big[\overline{\Delta}_{1}^{U} - \big(\mu^{U}+\mu^{L}\big)\Big] \Big)^{2} \pi_{k}^{L} \Bigg).\end{equation*}
The finiteness of the right-hand side yields
![]() $\overline{\sigma}^{2,U} < \infty$
. The proof that
$\overline{\sigma}^{2,U} < \infty$
. The proof that
![]() $\overline{\sigma}^{2,L} < \infty$
is similar.
$\overline{\sigma}^{2,L} < \infty$
is similar.
We finally establish that
![]() $\sigma^{2,U}$
,
$\sigma^{2,U}$
,
![]() $\sigma^{2,L}$
,
$\sigma^{2,L}$
,
![]() $\overline{\sigma}^{2,U}$
, and
$\overline{\sigma}^{2,U}$
, and
![]() $\overline{\sigma}^{2,L}$
are positive. We first show that, conditionally on
$\overline{\sigma}^{2,L}$
are positive. We first show that, conditionally on
![]() $Z_{0} \sim \delta_{i}^{L}$
and
$Z_{0} \sim \delta_{i}^{L}$
and
![]() $Z_{\tau_{1}} \sim \delta_{k}^{U}$
,
$Z_{\tau_{1}} \sim \delta_{k}^{U}$
,
![]() $\Delta_{1}^{U}$
and
$\Delta_{1}^{U}$
and
![]() $\Delta_{1}^{L}$
are non-degenerate. To this end, suppose for the sake of contradiction that
$\Delta_{1}^{L}$
are non-degenerate. To this end, suppose for the sake of contradiction that
Since
![]() $U_{1}$
has support
$U_{1}$
has support
![]() $S_{B}^{U}$
, we obtain that
$S_{B}^{U}$
, we obtain that
![]() $\mathbb{P}_{\delta_{i}^{L}}(Z_{\mu^{U}} \geq u, Z_{\mu^{U}-1} < u, \dots, Z_{1} < u)=1$
for all
$\mathbb{P}_{\delta_{i}^{L}}(Z_{\mu^{U}} \geq u, Z_{\mu^{U}-1} < u, \dots, Z_{1} < u)=1$
for all
![]() $u \in S_{B}^{U}$
. In particular,
$u \in S_{B}^{U}$
. In particular,
By taking both
![]() $u=L_{U}+1$
and
$u=L_{U}+1$
and
![]() $u \geq M^{U}(L_{U}+1)+N^{U}$
in the above equation, we obtain that both
$u \geq M^{U}(L_{U}+1)+N^{U}$
in the above equation, we obtain that both
![]() $\mathbb{E}_{\delta_{i}^{L}}[Z_{\mu^{U}-1}] < L_{U}+1$
and
$\mathbb{E}_{\delta_{i}^{L}}[Z_{\mu^{U}-1}] < L_{U}+1$
and
![]() $\mathbb{E}_{\delta_{i}^{L}}[Z_{\mu^{U}-1}] \geq L_{U}+1$
. Similarly, if
$\mathbb{E}_{\delta_{i}^{L}}[Z_{\mu^{U}-1}] \geq L_{U}+1$
. Similarly, if
 \begin{equation*} 1 = \mathbb{P}_{\delta_{k}^{U}}\big(\Delta_{1}^{L}=\mu^{L}\big) = \sum_{l=L_{0}}^{L_{U}} \mathbb{P}_{\delta_{k}^{U}}\big(Z_{\mu^{L}+\tau_{1}} \leq l, Z_{\mu^{L}+\tau_{1}-1} > l, \dots, Z_{\tau_{1}+1} > l\big) \mathbb{P}\big(L_{1}=l\big),\end{equation*}
\begin{equation*} 1 = \mathbb{P}_{\delta_{k}^{U}}\big(\Delta_{1}^{L}=\mu^{L}\big) = \sum_{l=L_{0}}^{L_{U}} \mathbb{P}_{\delta_{k}^{U}}\big(Z_{\mu^{L}+\tau_{1}} \leq l, Z_{\mu^{L}+\tau_{1}-1} > l, \dots, Z_{\tau_{1}+1} > l\big) \mathbb{P}\big(L_{1}=l\big),\end{equation*}
then using that
![]() $L_{1}$
has support
$L_{1}$
has support
![]() $\mathbb{N} \cap [L_{0}, L_{U}]$
, we obtain that
$\mathbb{N} \cap [L_{0}, L_{U}]$
, we obtain that
In particular,
By taking both
![]() $l=L_{0}$
and
$l=L_{0}$
and
![]() $l=L_{U}$
, we obtain that
$l=L_{U}$
, we obtain that
![]() $L_{0} > M^{L} L_{U}$
, which contradicts (
H4
). We deduce that
$L_{0} > M^{L} L_{U}$
, which contradicts (
H4
). We deduce that
 \begin{align*}\sum_{j=0}^{T_{i,1}^{L}-1}\big(\Delta_{j+1}^{U}-\mu^{U}\big)\end{align*}
\begin{align*}\sum_{j=0}^{T_{i,1}^{L}-1}\big(\Delta_{j+1}^{U}-\mu^{U}\big)\end{align*}
is non-degenerate, and similarly,
 \begin{equation*} \sum_{j=0}^{T_{i,1}^{U}-1} \big(\Delta_{j+1}^{L}-\mu^{L}\big), \qquad \sum_{j=0}^{T_{i,1}^{L}-1}\Big(\overline{\Delta}_{j+1}^{U}-\big(\mu^{U}+\mu^{L}\big)\Big), \quad \text{ and } \quad\sum_{j=0}^{T_{i,1}^{L}-1}\Big(\overline{\Delta}_{j+1}^{L}-(\mu^{L}+\mu^{U})\Big)\end{equation*}
\begin{equation*} \sum_{j=0}^{T_{i,1}^{U}-1} \big(\Delta_{j+1}^{L}-\mu^{L}\big), \qquad \sum_{j=0}^{T_{i,1}^{L}-1}\Big(\overline{\Delta}_{j+1}^{U}-\big(\mu^{U}+\mu^{L}\big)\Big), \quad \text{ and } \quad\sum_{j=0}^{T_{i,1}^{L}-1}\Big(\overline{\Delta}_{j+1}^{L}-(\mu^{L}+\mu^{U})\Big)\end{equation*}
are non-degenerate. Using Lemma 4.2 below, we conclude that
 \begin{equation*} \sigma^{2,U} = \pi_{i}^{L} \mathbb{V}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U}-\mu^{U}T_{i,1}^{L}\Big] =\pi_{i}^{L} \mathbb{E}_{\delta_{i}^{L}} \left[ \left( \sum_{j=0}^{T_{i,1}^{L}-1}\big(\Delta_{j+1}^{U}-\mu^{U}\big) \right)^{2} \right]>0,\end{equation*}
\begin{equation*} \sigma^{2,U} = \pi_{i}^{L} \mathbb{V}_{\delta_{i}^{L}}\Big[S_{T_{i,1}^{L}}^{U}-\mu^{U}T_{i,1}^{L}\Big] =\pi_{i}^{L} \mathbb{E}_{\delta_{i}^{L}} \left[ \left( \sum_{j=0}^{T_{i,1}^{L}-1}\big(\Delta_{j+1}^{U}-\mu^{U}\big) \right)^{2} \right]>0,\end{equation*}
and similarly
![]() $\sigma^{2,L}>0$
,
$\sigma^{2,L}>0$
,
![]() $\overline{\sigma}^{2,U} >0$
, and
$\overline{\sigma}^{2,U} >0$
, and
![]() $\overline{\sigma}^{2,L} >0$
.
$\overline{\sigma}^{2,L} >0$
.
A.6. Martingale structure of
 $\bf{M_{n,i}^{T}}$
$\bf{M_{n,i}^{T}}$
We recall that
![]() $M_{n,i}^{T} \;:\!=\; \sum_{j=1}^{n} D_{j,i}^{T}$
, where
$M_{n,i}^{T} \;:\!=\; \sum_{j=1}^{n} D_{j,i}^{T}$
, where
 \begin{equation*} D_{j,1}^{T} = \Big(\overline{P}_{j-1}^{T}-M^{T}\Big) \tilde{\chi}_{j-1}^T \quad \text{ and } \quad D_{j,2}^{T} = \frac{\tilde{\chi}_{j-1}^{T}}{Z_{j-1}} \sum_{i=1}^{Z_{j-1}} \Big( \xi_{j-1,i}^{T} - \overline{P}_{j-1}^{T}\Big).\end{equation*}
\begin{equation*} D_{j,1}^{T} = \Big(\overline{P}_{j-1}^{T}-M^{T}\Big) \tilde{\chi}_{j-1}^T \quad \text{ and } \quad D_{j,2}^{T} = \frac{\tilde{\chi}_{j-1}^{T}}{Z_{j-1}} \sum_{i=1}^{Z_{j-1}} \Big( \xi_{j-1,i}^{T} - \overline{P}_{j-1}^{T}\Big).\end{equation*}
Also,
 \begin{align*}\tilde{A}_{n}^{T} = \sum_{j=1}^n \frac{\tilde{\chi}_{j-1}^T}{Z_{j-1}},\end{align*}
\begin{align*}\tilde{A}_{n}^{T} = \sum_{j=1}^n \frac{\tilde{\chi}_{j-1}^T}{Z_{j-1}},\end{align*}
and for
![]() $s \geq 0$
,
$s \geq 0$
,
Proposition A.3. The following statements hold:
-
(i) For
 $i=1,2$
,
$i=1,2$
,
 $\{ (M_{n,1}^{T}, \mathcal{H}_{n,i}) \}_{n=1}^{\infty}$
is a mean-zero martingale sequence, and for all
$\{ (M_{n,1}^{T}, \mathcal{H}_{n,i}) \}_{n=1}^{\infty}$
is a mean-zero martingale sequence, and for all
 $s \geq 0$
, we have
$s \geq 0$
, we have
 $\mathbb{E}\big[\lvert D_{j,1}^{T}\rvert^{s} | \mathcal{H}_{j-1,i} \big] = \mathbb{E}\big[\Lambda_{0,1}^{T,s}\big] \tilde{\chi}_{j-1}^{T}$
a.s. In particular,
$\mathbb{E}\big[\lvert D_{j,1}^{T}\rvert^{s} | \mathcal{H}_{j-1,i} \big] = \mathbb{E}\big[\Lambda_{0,1}^{T,s}\big] \tilde{\chi}_{j-1}^{T}$
a.s. In particular,  \begin{equation*} \mathbb{E}\big[\big(D_{j,1}^{T}\big)^{2} | \mathcal{H}_{j-1,i}\big]=V_{1}^{T} \tilde{\chi}_{j-1}^{T} \textit{ a.s., and } \mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big]=V_{1}^{T} \mathbb{E}\big[\tilde{C}_{n}^{T}\big].\end{equation*}
\begin{equation*} \mathbb{E}\big[\big(D_{j,1}^{T}\big)^{2} | \mathcal{H}_{j-1,i}\big]=V_{1}^{T} \tilde{\chi}_{j-1}^{T} \textit{ a.s., and } \mathbb{E}\big[\big(M_{n,1}^{T}\big)^{2}\big]=V_{1}^{T} \mathbb{E}\big[\tilde{C}_{n}^{T}\big].\end{equation*}
-
(ii)
 $\big\{ (M_{n,2}^{T}, \mathcal{H}_{n,2}) \big\}_{n=1}^{\infty}$
is a mean-zero martingale sequence satisfying Additionally, for all
$\big\{ (M_{n,2}^{T}, \mathcal{H}_{n,2}) \big\}_{n=1}^{\infty}$
is a mean-zero martingale sequence satisfying Additionally, for all \begin{equation*} \mathbb{E}\big[\big(D_{j,2}^{T}\big)^{2} | \mathcal{H}_{j-1,2}\big]=V_{2}^{T} \frac{\tilde{\chi}_{j-1}^T}{Z_{j-1}} \textit{a.s., and } \mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big]= V_{2}^{T} \mathbb{E}\big[ \tilde{A}_{n}^{T} \big].\end{equation*}
\begin{equation*} \mathbb{E}\big[\big(D_{j,2}^{T}\big)^{2} | \mathcal{H}_{j-1,2}\big]=V_{2}^{T} \frac{\tilde{\chi}_{j-1}^T}{Z_{j-1}} \textit{a.s., and } \mathbb{E}\big[\big(M_{n,2}^{T}\big)^{2}\big]= V_{2}^{T} \mathbb{E}\big[ \tilde{A}_{n}^{T} \big].\end{equation*}
 $s \geq 1$
,
$s \geq 1$
,
 $\mathbb{E}\big[\lvert D_{j,2}^{T}\rvert^{s} | \mathcal{H}_{j-1,2}\big] \leq \mathbb{E}\big[\Lambda_{0,2}^{T,s}\big] \tilde{\chi}_{j-1}^T$
a.s.
$\mathbb{E}\big[\lvert D_{j,2}^{T}\rvert^{s} | \mathcal{H}_{j-1,2}\big] \leq \mathbb{E}\big[\Lambda_{0,2}^{T,s}\big] \tilde{\chi}_{j-1}^T$
a.s.
-
(iii) For
 $i=1,2$
,
$i=1,2$
,
 $\big\{\big(\sum_{j=1}^{n} \big(\big(D_{j,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{j,i}^{T}\big)^{2}\big]\big), \tilde{\mathcal{H}}_{n,i}\big)\big\}_{n=1}^{\infty}$
are mean-zero martingale sequences, and for all
$\big\{\big(\sum_{j=1}^{n} \big(\big(D_{j,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{j,i}^{T}\big)^{2}\big]\big), \tilde{\mathcal{H}}_{n,i}\big)\big\}_{n=1}^{\infty}$
are mean-zero martingale sequences, and for all
 $s \geq 1$
,
$s \geq 1$
,  \begin{equation*} \mathbb{E} \big[ \lvert \big(D_{j,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{j,i}^{T}\big)^{2}\big] \rvert^{s} | \tilde{\mathcal{H}}_{j-1,i} \big] \leq 2^{s} \mathbb{E}\big[\Lambda_{0,i}^{T,2s}\big] \mathbb{E}\big[ \tilde{\chi}_{j-1}^{T}\big].\end{equation*}
\begin{equation*} \mathbb{E} \big[ \lvert \big(D_{j,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{j,i}^{T}\big)^{2}\big] \rvert^{s} | \tilde{\mathcal{H}}_{j-1,i} \big] \leq 2^{s} \mathbb{E}\big[\Lambda_{0,i}^{T,2s}\big] \mathbb{E}\big[ \tilde{\chi}_{j-1}^{T}\big].\end{equation*}
-
(iv) For all
 $T_{1},T_{2} \in \{ L,U \}$
and
$T_{1},T_{2} \in \{ L,U \}$
and
 $i_{1},i_{2} \in \{ 1,2\}$
such that either
$i_{1},i_{2} \in \{ 1,2\}$
such that either
 $T_{1} \neq T_{2}$
or
$T_{1} \neq T_{2}$
or
 $i_{1} \neq i_{2}$
, it holds that
$i_{1} \neq i_{2}$
, it holds that
 $\mathbb{E}\big[\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{l,i_{2}}^{T_{2}}\big)\big]=0$
for all
$\mathbb{E}\big[\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{l,i_{2}}^{T_{2}}\big)\big]=0$
for all
 $j,l =1,\dots,n$
and
$j,l =1,\dots,n$
and
 $\mathbb{E}\big[\big(M_{n,i_{1}}^{T_{1}}\big)\big(M_{n,i_{2}}^{T_{2}}\big)\big]=0$
. In particular,
$\mathbb{E}\big[\big(M_{n,i_{1}}^{T_{1}}\big)\big(M_{n,i_{2}}^{T_{2}}\big)\big]=0$
. In particular,
 $\big\{ \big(\sum_{j=1}^{n} \big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big), \tilde{\mathcal{H}}_{n,2}\big) \big\}_{n=0}^{\infty}$
is a mean-zero martingale sequence, and for all
$\big\{ \big(\sum_{j=1}^{n} \big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big), \tilde{\mathcal{H}}_{n,2}\big) \big\}_{n=0}^{\infty}$
is a mean-zero martingale sequence, and for all
 $s \geq 1$
,
$s \geq 1$
,  \begin{equation*} \mathbb{E}\big[\lvert\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big)\rvert^{s} | \tilde{\mathcal{H}}_{j-1,2}\big] \leq \mathbb{E}\big[\Lambda_{0,i_{1}}^{T_{1},s} \Lambda_{0,i_{2}}^{T_{2},s}\big] \mathbb{E}\big[\tilde{\chi}_{j-1}^{T_{1}} \tilde{\chi}_{j-1}^{T_{2}}\big].\end{equation*}
\begin{equation*} \mathbb{E}\big[\lvert\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big)\rvert^{s} | \tilde{\mathcal{H}}_{j-1,2}\big] \leq \mathbb{E}\big[\Lambda_{0,i_{1}}^{T_{1},s} \Lambda_{0,i_{2}}^{T_{2},s}\big] \mathbb{E}\big[\tilde{\chi}_{j-1}^{T_{1}} \tilde{\chi}_{j-1}^{T_{2}}\big].\end{equation*}
Proof of Proposition
A.3. We begin by proving (i) with
![]() $i=1$
. We notice that
$i=1$
. We notice that
![]() $\big(M_{n,1}^{T}, \mathcal{H}_{n,i}\big)$
is a martingale, since
$\big(M_{n,1}^{T}, \mathcal{H}_{n,i}\big)$
is a martingale, since
![]() $M_{n,1}^{T}$
is
$M_{n,1}^{T}$
is
![]() $\mathcal{H}_{n,1}$
-measurable and
$\mathcal{H}_{n,1}$
-measurable and
It follows that
![]() $\mathbb{E}\big[M_{n,1}^{T}\big] = \mathbb{E}\big[M_{1,1}^{T}\big] = 0$
. Next, notice that for
$\mathbb{E}\big[M_{n,1}^{T}\big] = \mathbb{E}\big[M_{1,1}^{T}\big] = 0$
. Next, notice that for
![]() $s \geq 0$
,
$s \geq 0$
,
In particular, if
![]() $s=2$
, then
$s=2$
, then
![]() $\mathbb{E}\big[\big(D_{j,1}^{T}\big)^{2} | \mathcal{H}_{j-1,1}\big]=V_{1}^{T} \tilde{\chi}_{j-1}^T$
a.s., and the martingale property yields that
$\mathbb{E}\big[\big(D_{j,1}^{T}\big)^{2} | \mathcal{H}_{j-1,1}\big]=V_{1}^{T} \tilde{\chi}_{j-1}^T$
a.s., and the martingale property yields that
 \begin{equation*} \mathbb{E}[\big(M_{n,1}^{T}\big)^{2} = \mathbb{E} \Bigg[ \sum_{j=1}^{n} \mathbb{E}\big[\big(D_{j,1}^{T}\big)^{2} | \mathcal{H}_{j-1,1}\big] \Bigg] = V_{1}^{T} \mathbb{E}[\tilde{C}_{n}^{T}].\end{equation*}
\begin{equation*} \mathbb{E}[\big(M_{n,1}^{T}\big)^{2} = \mathbb{E} \Bigg[ \sum_{j=1}^{n} \mathbb{E}\big[\big(D_{j,1}^{T}\big)^{2} | \mathcal{H}_{j-1,1}\big] \Bigg] = V_{1}^{T} \mathbb{E}[\tilde{C}_{n}^{T}].\end{equation*}
Finally, we notice that, since the
![]() $D_{j,1}^{T}$
do not depend on the offspring distributions
$D_{j,1}^{T}$
do not depend on the offspring distributions
![]() $\{ \xi_{j,i}^{T}) \}_{i=0}^{\infty}$
, Part (i) holds with
$\{ \xi_{j,i}^{T}) \}_{i=0}^{\infty}$
, Part (i) holds with
![]() $\mathcal{H}_{n,1}$
replaced by
$\mathcal{H}_{n,1}$
replaced by
![]() $\mathcal{H}_{n,2}$
.
$\mathcal{H}_{n,2}$
.
We now turn to the proof of (ii). We notice that
![]() $M_{n,2}^{T}$
is
$M_{n,2}^{T}$
is
![]() $\mathcal{H}_{n,2}$
-measurable, and using that
$\mathcal{H}_{n,2}$
-measurable, and using that
![]() $\mathbb{E}[ \xi_{n-1,i}^{T} - \overline{P}_{n-1}^{T} | \Pi_{n-1}^{T}] =0$
, we obtain that
$\mathbb{E}[ \xi_{n-1,i}^{T} - \overline{P}_{n-1}^{T} | \Pi_{n-1}^{T}] =0$
, we obtain that
 \begin{equation*} \mathbb{E}\big[M_{n,2}^{T} | \mathcal{H}_{n-1,2}\big] = M_{n-1,2}^{T} + \frac{\tilde{\chi}_{n-1}^{T}}{Z_{n-1}} \sum_{i=1}^{Z_{n-1}} \mathbb{E}\big[ \mathbb{E}\big[ \xi_{n-1,i}^{T} - \overline{P}_{n-1}^{T} | \Pi_{n-1}^{T}\big] \big] = M_{n-1,2}^{T},\end{equation*}
\begin{equation*} \mathbb{E}\big[M_{n,2}^{T} | \mathcal{H}_{n-1,2}\big] = M_{n-1,2}^{T} + \frac{\tilde{\chi}_{n-1}^{T}}{Z_{n-1}} \sum_{i=1}^{Z_{n-1}} \mathbb{E}\big[ \mathbb{E}\big[ \xi_{n-1,i}^{T} - \overline{P}_{n-1}^{T} | \Pi_{n-1}^{T}\big] \big] = M_{n-1,2}^{T},\end{equation*}
yielding the martingale property. It follows that
![]() $\mathbb{E}\big[M_{n,2}^{T}\big] = \mathbb{E}\big[M_{1,2}^{T}\big]=0$
, as
$\mathbb{E}\big[M_{n,2}^{T}\big] = \mathbb{E}\big[M_{1,2}^{T}\big]=0$
, as
 \begin{equation*} \mathbb{E}\big[M_{1,2}^{T} | \mathcal{H}_{0,2}\big] = \frac{\tilde{\chi}_{0}^{T}}{Z_{0}} \sum_{i=1}^{Z_{0}} \mathbb{E}\big[ \mathbb{E}\big[ \xi_{0,i}^{T} - \overline{P}_{0}^{T} | \Pi_{0}^{T}\big]\big] = 0.\end{equation*}
\begin{equation*} \mathbb{E}\big[M_{1,2}^{T} | \mathcal{H}_{0,2}\big] = \frac{\tilde{\chi}_{0}^{T}}{Z_{0}} \sum_{i=1}^{Z_{0}} \mathbb{E}\big[ \mathbb{E}\big[ \xi_{0,i}^{T} - \overline{P}_{0}^{T} | \Pi_{0}^{T}\big]\big] = 0.\end{equation*}
We now compute
 \begin{equation*} \mathbb{E}\big[\big(D_{j,2}^{T}\big)^{2} | \mathcal{H}_{j-1,2}\big] = \frac{\tilde{\chi}_{j-1}^{T}}{Z_{j-1}^{2}} \mathbb{E} \!\left[ \mathbb{E} \!\left[ \left( \sum_{i=1}^{Z_{j-1}} \big(\xi_{j-1,i}^{T} - \overline{P}_{j-1}^{T}\big) \right)^{2} | \mathcal{H}_{j-1,2},\Pi_{j-1}^{T} \right] | \mathcal{H}_{j-1,2} \right].\end{equation*}
\begin{equation*} \mathbb{E}\big[\big(D_{j,2}^{T}\big)^{2} | \mathcal{H}_{j-1,2}\big] = \frac{\tilde{\chi}_{j-1}^{T}}{Z_{j-1}^{2}} \mathbb{E} \!\left[ \mathbb{E} \!\left[ \left( \sum_{i=1}^{Z_{j-1}} \big(\xi_{j-1,i}^{T} - \overline{P}_{j-1}^{T}\big) \right)^{2} | \mathcal{H}_{j-1,2},\Pi_{j-1}^{T} \right] | \mathcal{H}_{j-1,2} \right].\end{equation*}
Using that, conditionally on the environment
![]() $\Pi_{j-1}^T$
,
$\Pi_{j-1}^T$
,
![]() $\{ \xi_{j-1,i}^T \}_{i=1}^{\infty}$
are i.i.d. with variance
$\{ \xi_{j-1,i}^T \}_{i=1}^{\infty}$
are i.i.d. with variance
![]() $\overline{\overline{P}}_{j-1}^{T}$
, we obtain that
$\overline{\overline{P}}_{j-1}^{T}$
, we obtain that
 \begin{align*} \mathbb{E} \left[ \left( \sum_{i=1}^{Z_{j-1}} \xi_{j-1,i}^T - \overline{P}_{j-1}^{T} \right)^2 | \mathcal{H}_{j-1,2}, \Pi_{j-1}^{T} \right] &= \sum_{i=1}^{Z_{j-1}} \mathbb{E} \left[ \big(\xi_{j-1,i}^T - \overline{P}_{j-1}^{T}\big)^2 | \mathcal{H}_{j-1,2}, \Pi_{j-1}^{T} \right] \\[5pt] &= Z_{j-1} \overline{\overline{P}}_{j-1}^{T}.\end{align*}
\begin{align*} \mathbb{E} \left[ \left( \sum_{i=1}^{Z_{j-1}} \xi_{j-1,i}^T - \overline{P}_{j-1}^{T} \right)^2 | \mathcal{H}_{j-1,2}, \Pi_{j-1}^{T} \right] &= \sum_{i=1}^{Z_{j-1}} \mathbb{E} \left[ \big(\xi_{j-1,i}^T - \overline{P}_{j-1}^{T}\big)^2 | \mathcal{H}_{j-1,2}, \Pi_{j-1}^{T} \right] \\[5pt] &= Z_{j-1} \overline{\overline{P}}_{j-1}^{T}.\end{align*}
We conclude that
and
 \begin{equation*} \mathbb{E}\Big[\Big(M_{n,2}^{T}\Big)^{2}\Big] = \mathbb{E} \Bigg[ \sum_{j=1}^{n} \mathbb{E}\big[\big(D_{j,2}^{T}\big)^{2} | \mathcal{H}_{j-1,2}\big] \Bigg] = V_{2}^{T} \mathbb{E}\big[ \tilde{A}_{n}^{T} \big].\end{equation*}
\begin{equation*} \mathbb{E}\Big[\Big(M_{n,2}^{T}\Big)^{2}\Big] = \mathbb{E} \Bigg[ \sum_{j=1}^{n} \mathbb{E}\big[\big(D_{j,2}^{T}\big)^{2} | \mathcal{H}_{j-1,2}\big] \Bigg] = V_{2}^{T} \mathbb{E}\big[ \tilde{A}_{n}^{T} \big].\end{equation*}
Additionally, Jensen’s inequality yields that for
![]() $s \geq 1$
,
$s \geq 1$
,
 \begin{equation*} \mathbb{E}\big[\big\lvert D_{j,2}^{T}\big\rvert^{s} \big| \mathcal{H}_{j-1,2}\big] \leq \mathbb{E} \Bigg[ \frac{\tilde{\chi}_{j-1}^{T}}{Z_{j-1}} \sum_{i=1}^{Z_{j-1}} \big\lvert\xi_{j-1,i}^{T} - \overline{P}_{j-1}^{T}\big\rvert^{s} | \mathcal{H}_{j-1,2} \Bigg] = \mathbb{E}\big[\Lambda_{0,2}^{T,s}\big] \tilde{\chi}_{j-1}^T \text{ a.s.}\end{equation*}
\begin{equation*} \mathbb{E}\big[\big\lvert D_{j,2}^{T}\big\rvert^{s} \big| \mathcal{H}_{j-1,2}\big] \leq \mathbb{E} \Bigg[ \frac{\tilde{\chi}_{j-1}^{T}}{Z_{j-1}} \sum_{i=1}^{Z_{j-1}} \big\lvert\xi_{j-1,i}^{T} - \overline{P}_{j-1}^{T}\big\rvert^{s} | \mathcal{H}_{j-1,2} \Bigg] = \mathbb{E}\big[\Lambda_{0,2}^{T,s}\big] \tilde{\chi}_{j-1}^T \text{ a.s.}\end{equation*}
For (iii), we notice that
![]() $\sum_{j=1}^{n} \big(\big(D_{j,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{j,i}^{T}\big)^{2}\big]\big)$
is
$\sum_{j=1}^{n} \big(\big(D_{j,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{j,i}^{T}\big)^{2}\big]\big)$
is
![]() $\tilde{\mathcal{H}}_{n,i}$
-measurable, and since
$\tilde{\mathcal{H}}_{n,i}$
-measurable, and since
![]() $\tilde{\chi}_{n-1}^{T}$
,
$\tilde{\chi}_{n-1}^{T}$
,
![]() $Z_{n-1}$
,
$Z_{n-1}$
,
![]() $\Pi_{n-1}^{T}$
, and
$\Pi_{n-1}^{T}$
, and
![]() $\big\{ \xi_{n-1,i}^{T} \big\}_{i=0}^{\infty}$
are not
$\big\{ \xi_{n-1,i}^{T} \big\}_{i=0}^{\infty}$
are not
![]() $\tilde{\mathcal{H}}_{n-1,i}$
-measurable, we have that
$\tilde{\mathcal{H}}_{n-1,i}$
-measurable, we have that
![]() $\mathbb{E}\big[\big(D_{n,i}^{T}\big)^{2} | \tilde{\mathcal{H}}_{n-1,i}\big]=\mathbb{E}\big[\big(D_{n,i}^{T}\big)^{2}\big]$
and
$\mathbb{E}\big[\big(D_{n,i}^{T}\big)^{2} | \tilde{\mathcal{H}}_{n-1,i}\big]=\mathbb{E}\big[\big(D_{n,i}^{T}\big)^{2}\big]$
and
 \begin{equation*} \mathbb{E} \Bigg[ \sum_{j=1}^{n} \big(\big(D_{j,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{j,i}^{T}\big)^{2}\big]\big) | \tilde{\mathcal{H}}_{n-1,i} \Bigg] = \sum_{j=1}^{n-1} \big(\big(D_{j,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{j,i}^{T}\big)^{2}\big]\big).\end{equation*}
\begin{equation*} \mathbb{E} \Bigg[ \sum_{j=1}^{n} \big(\big(D_{j,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{j,i}^{T}\big)^{2}\big]\big) | \tilde{\mathcal{H}}_{n-1,i} \Bigg] = \sum_{j=1}^{n-1} \big(\big(D_{j,i}^{T}\big)^{2}-\mathbb{E}\big[\big(D_{j,i}^{T}\big)^{2}\big]\big).\end{equation*}
Again using the convexity of the function
![]() $\lvert\cdot\rvert^{s}$
for
$\lvert\cdot\rvert^{s}$
for
![]() $s \geq 1$
, we get that
$s \geq 1$
, we get that
If
![]() $i=1$
, then by conditioning on
$i=1$
, then by conditioning on
![]() $\tilde{\chi}_{j-1}^{T}$
we have that
$\tilde{\chi}_{j-1}^{T}$
we have that
![]() $\mathbb{E}\big[\big(D_{j,1}^{T}\big)^{2s} \big] = \mathbb{E}\big[\Lambda_{0,1}^{T,2s}\big] \mathbb{E}\big[ \tilde{\chi}_{j-1}^{T}\big]$
. If
$\mathbb{E}\big[\big(D_{j,1}^{T}\big)^{2s} \big] = \mathbb{E}\big[\Lambda_{0,1}^{T,2s}\big] \mathbb{E}\big[ \tilde{\chi}_{j-1}^{T}\big]$
. If
![]() $i=2$
, then we apply Jensen’s inequality and obtain that
$i=2$
, then we apply Jensen’s inequality and obtain that
Turning to (iv), we show that for all
![]() $T_{1},T_{2} \in \{ L,U \}$
and
$T_{1},T_{2} \in \{ L,U \}$
and
![]() $i_{1},i_{2} \in \{ 1,2\}$
such that either
$i_{1},i_{2} \in \{ 1,2\}$
such that either
![]() $T_{1} \neq T_{2}$
or
$T_{1} \neq T_{2}$
or
![]() $i_{1} \neq i_{2}$
, it holds that
$i_{1} \neq i_{2}$
, it holds that
![]() $\mathbb{E}\big[\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{l,i_{2}}^{T_{2}}\big)\big]=0$
for all
$\mathbb{E}\big[\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{l,i_{2}}^{T_{2}}\big)\big]=0$
for all
![]() $j,l =1,\dots,n$
. This also yields that
$j,l =1,\dots,n$
. This also yields that
 \begin{equation*} \mathbb{E}\big[\big(M_{n,i_{1}}^{T_{1}}\big)\big(M_{n,i_{2}}^{T_{2}}\big)\big] = \sum_{j=1}^{n} \sum_{l=1}^{n} \mathbb{E}\big[\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{l,i_{2}}^{T_{2}}\big)\big] = 0.\end{equation*}
\begin{equation*} \mathbb{E}\big[\big(M_{n,i_{1}}^{T_{1}}\big)\big(M_{n,i_{2}}^{T_{2}}\big)\big] = \sum_{j=1}^{n} \sum_{l=1}^{n} \mathbb{E}\big[\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{l,i_{2}}^{T_{2}}\big)\big] = 0.\end{equation*}
First, if
![]() $l=j$
and
$l=j$
and
![]() $T_{1} \neq T_{2}$
, then
$T_{1} \neq T_{2}$
, then
![]() $\mathbb{E}\big[\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big)\big]=0$
because
$\mathbb{E}\big[\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big)\big]=0$
because
![]() $\tilde{\chi}_{j-1}^{T_{1}} \tilde{\chi}_{j-1}^{T_{2}}=0$
. Next, if
$\tilde{\chi}_{j-1}^{T_{1}} \tilde{\chi}_{j-1}^{T_{2}}=0$
. Next, if
![]() $l=j$
and
$l=j$
and
![]() $i_{1} \neq i_{2}$
(say
$i_{1} \neq i_{2}$
(say
![]() $i_{1}=1$
or
$i_{1}=1$
or
![]() $i_{2}=2$
), then by conditioning on
$i_{2}=2$
), then by conditioning on
![]() $\mathcal{H}_{j-1,1}$
and
$\mathcal{H}_{j-1,1}$
and
![]() $\Pi_{j-1}^{T_{2}}$
and using the fact that
$\Pi_{j-1}^{T_{2}}$
and using the fact that
and that
![]() $\Pi_{j-1}^{T_{1}}$
,
$\Pi_{j-1}^{T_{1}}$
,
![]() $\tilde{\chi}_{j-1}^{T_{1}}$
,
$\tilde{\chi}_{j-1}^{T_{1}}$
,
![]() $\tilde{\chi}_{j-1}^{T_{2}}$
, and
$\tilde{\chi}_{j-1}^{T_{2}}$
, and
![]() $Z_{j-1}$
are
$Z_{j-1}$
are
![]() $\mathcal{H}_{j-1,1}$
-measurable, we obtain that
$\mathcal{H}_{j-1,1}$
-measurable, we obtain that
 \begin{equation*} \mathbb{E}\big[\big(D_{j,1}^{T_{1}}\big)\big(D_{j,2}^{T_{2}}\big)\big] = \mathbb{E} \left[ \Big(\overline{P}_{j-1}^{T_{1}}-M^{T_{1}}\Big) \tilde{\chi}_{j-1}^{T_{1}} \frac{\tilde{\chi}_{j-1}^{T_{2}}}{Z_{j-1}} \sum_{i=1}^{Z_{j-1}} \mathbb{E} \left[\xi_{j-1,i}^{T_{2}} - \overline{P}_{j-1}^{T_{2}} | \mathcal{H}_{j-1,1}, \Pi_{j-1}^{T_{2}} \right] \right] =0.\end{equation*}
\begin{equation*} \mathbb{E}\big[\big(D_{j,1}^{T_{1}}\big)\big(D_{j,2}^{T_{2}}\big)\big] = \mathbb{E} \left[ \Big(\overline{P}_{j-1}^{T_{1}}-M^{T_{1}}\Big) \tilde{\chi}_{j-1}^{T_{1}} \frac{\tilde{\chi}_{j-1}^{T_{2}}}{Z_{j-1}} \sum_{i=1}^{Z_{j-1}} \mathbb{E} \left[\xi_{j-1,i}^{T_{2}} - \overline{P}_{j-1}^{T_{2}} | \mathcal{H}_{j-1,1}, \Pi_{j-1}^{T_{2}} \right] \right] =0.\end{equation*}
Finally, if
![]() $l \neq j$
(say
$l \neq j$
(say
![]() $l > j$
), then by conditioning on
$l > j$
), then by conditioning on
![]() $\tilde{\mathcal{H}}_{l-1,2}$
and using that
$\tilde{\mathcal{H}}_{l-1,2}$
and using that
![]() $D_{j,i_{1}}$
is
$D_{j,i_{1}}$
is
![]() $\tilde{\mathcal{H}}_{l-1,2}$
-measurable and
$\tilde{\mathcal{H}}_{l-1,2}$
-measurable and
![]() $\mathbb{E}[(D_{l,i_{2}}) | \tilde{\mathcal{H}}_{l-1,2} ]=\mathbb{E}[D_{l,i_{2}}]=0$
, we obtain that
$\mathbb{E}[(D_{l,i_{2}}) | \tilde{\mathcal{H}}_{l-1,2} ]=\mathbb{E}[D_{l,i_{2}}]=0$
, we obtain that
We have that
![]() $\{ \big(\sum_{j=1}^{n} \big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big), \tilde{\mathcal{H}}_{n,2}\big) \}_{n=0}^{\infty}$
is a mean-zero martingale sequence, since
$\{ \big(\sum_{j=1}^{n} \big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big), \tilde{\mathcal{H}}_{n,2}\big) \}_{n=0}^{\infty}$
is a mean-zero martingale sequence, since
![]() $\sum_{j=1}^{n} \big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big)$
is
$\sum_{j=1}^{n} \big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big)$
is
![]() $\tilde{\mathcal{H}}_{n,2}$
-measurable and
$\tilde{\mathcal{H}}_{n,2}$
-measurable and
if either
![]() $T_{1} \neq T_{2}$
or
$T_{1} \neq T_{2}$
or
![]() $i_{1} \neq i_{2}$
. If
$i_{1} \neq i_{2}$
. If
![]() $T_{1} \neq T_{2}$
, then both
$T_{1} \neq T_{2}$
, then both
![]() $\mathbb{E}\big[\lvert\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big)\rvert^{s} | \tilde{\mathcal{H}}_{j-1,2}\big]=0$
and
$\mathbb{E}\big[\lvert\big(D_{j,i_{1}}^{T_{1}}\big)\big(D_{j,i_{2}}^{T_{2}}\big)\rvert^{s} | \tilde{\mathcal{H}}_{j-1,2}\big]=0$
and
![]() $\mathbb{E}\big[\tilde{\chi}_{j-1}^{T_{1}} \tilde{\chi}_{j-1}^{T_{2}}\big]=0$
. Finally, if
$\mathbb{E}\big[\tilde{\chi}_{j-1}^{T_{1}} \tilde{\chi}_{j-1}^{T_{2}}\big]=0$
. Finally, if
![]() $T_{1} = T_{2}$
and
$T_{1} = T_{2}$
and
![]() $i_{1} \neq i_{2}$
(say
$i_{1} \neq i_{2}$
(say
![]() $i_{1}=1$
and
$i_{1}=1$
and
![]() $i_{2}=2$
), then by Jensen’s inequality
$i_{2}=2$
), then by Jensen’s inequality
which yields that
and
Appendix B. Numerical experiments
In this section we describe numerical experiments to illustrate the evolution of the process under different distributional assumptions. We also study the empirical distribution of the lengths of supercritical and subcritical regimes and illustrate how the process changes when
![]() $U_{j}$
and
$U_{j}$
and
![]() $L_{j}$
exhibit an increasing trend. We emphasize that these experiments illustrate the behavior of the estimates of the parameters of the BPRET when using a finite number of generations in a single synthetic dataset. In the numerical experiments 1–4 below, we set
$L_{j}$
exhibit an increasing trend. We emphasize that these experiments illustrate the behavior of the estimates of the parameters of the BPRET when using a finite number of generations in a single synthetic dataset. In the numerical experiments 1–4 below, we set
![]() $L_{0} = 10^{2}$
,
$L_{0} = 10^{2}$
,
![]() $L_{U}=10^{4}$
,
$L_{U}=10^{4}$
,
![]() $n \in \{0,1,\dots,10^4\}$
,
$n \in \{0,1,\dots,10^4\}$
,
![]() $U_{j} \sim L_{U}+\texttt{Zeta}(3)$
,
$U_{j} \sim L_{U}+\texttt{Zeta}(3)$
,
![]() $L_{j} \sim \texttt{Unif}_{d}(L_{0},10 L_{0})$
, and we use different distributions for
$L_{j} \sim \texttt{Unif}_{d}(L_{0},10 L_{0})$
, and we use different distributions for
![]() $Z_{0}$
,
$Z_{0}$
,
![]() $I_{0}^{U} \sim Q_{0}^{U}$
,
$I_{0}^{U} \sim Q_{0}^{U}$
,
![]() $\xi_{0,1}^{U} \sim P_{0}^{U}$
, and
$\xi_{0,1}^{U} \sim P_{0}^{U}$
, and
![]() $\xi_{0,1}^{L} \sim P_{0}^{L}$
as follows:
$\xi_{0,1}^{L} \sim P_{0}^{L}$
as follows:

In the above description, we have used the notation
![]() $\texttt{Unif}(a,b)$
for the uniform distribution over the interval (a,b) and
$\texttt{Unif}(a,b)$
for the uniform distribution over the interval (a,b) and
![]() $\texttt{Unif}_{d}(a,b)$
for the uniform distribution over integers between a and b.
$\texttt{Unif}_{d}(a,b)$
for the uniform distribution over integers between a and b.
![]() $\texttt{Zeta}(s)$
is the zeta distribution with exponent
$\texttt{Zeta}(s)$
is the zeta distribution with exponent
![]() $s>1$
.
$s>1$
.
![]() $\texttt{Pois}(\lambda)$
is the Poisson distribution with parameter
$\texttt{Pois}(\lambda)$
is the Poisson distribution with parameter
![]() $\lambda$
, while
$\lambda$
, while
![]() $\texttt{Pois}(\lambda;b)$
is the Poisson distribution truncated to values not larger than b. Similarly,
$\texttt{Pois}(\lambda;b)$
is the Poisson distribution truncated to values not larger than b. Similarly,
![]() $\texttt{Nbin}(r,o)$
is the negative binomial distribution with predefined number of successful trials r and mean o, while
$\texttt{Nbin}(r,o)$
is the negative binomial distribution with predefined number of successful trials r and mean o, while
![]() $\texttt{Nbin}(r,o;b)$
is the negative binomial distribution truncated to values not larger than b. Finally,
$\texttt{Nbin}(r,o;b)$
is the negative binomial distribution truncated to values not larger than b. Finally,
![]() $\texttt{Gamma}(\alpha,\beta)$
is the gamma distribution with shape parameter
$\texttt{Gamma}(\alpha,\beta)$
is the gamma distribution with shape parameter
![]() $\alpha$
and rate parameter
$\alpha$
and rate parameter
![]() $\beta$
. In these experiments, there were between 400 and 700 crossings of the thresholds, depending on the distributional assumptions. The results of the numerical experiments 1–4 are shown in Figure 2.
$\beta$
. In these experiments, there were between 400 and 700 crossings of the thresholds, depending on the distributional assumptions. The results of the numerical experiments 1–4 are shown in Figure 2.
We next turn our attention to the construction of confidence intervals for the means in the supercritical and subcritical regimes. The values of
![]() $M^{T}=\mathbb{E}[\overline{P}_{0}^{T}]$
,
$M^{T}=\mathbb{E}[\overline{P}_{0}^{T}]$
,
![]() $V_{1}^{T}=\mathbb{V}[\overline{P}_{0}^{T}]$
, and
$V_{1}^{T}=\mathbb{V}[\overline{P}_{0}^{T}]$
, and
![]() $V_{2}^{T}=\mathbb{E}[\overline{\overline{P}}_{0}^{T}]$
in Experiments 1–4 can be deduced from the underlying distributions and are summarized below. The values of
$V_{2}^{T}=\mathbb{E}[\overline{\overline{P}}_{0}^{T}]$
in Experiments 1–4 can be deduced from the underlying distributions and are summarized below. The values of
![]() $V_{2}^{U}$
and
$V_{2}^{U}$
and
![]() $V_{2}^{L}$
in Experiments 3–4 are rounded to three decimal digits.
$V_{2}^{L}$
in Experiments 3–4 are rounded to three decimal digits.

In the next table, we provide the estimators
![]() $M_{n}^{U}$
,
$M_{n}^{U}$
,
![]() $C_{n}^{U}/\tilde{N}^{L}(n)$
,
$C_{n}^{U}/\tilde{N}^{L}(n)$
,
![]() $\tilde{C}_{n}^{U}/\tilde{N}^{L}(n)$
, and
$\tilde{C}_{n}^{U}/\tilde{N}^{L}(n)$
, and
![]() $\tilde{A}_{n}^{U}/\tilde{N}^{L}(n)$
of
$\tilde{A}_{n}^{U}/\tilde{N}^{L}(n)$
of
![]() $\mathbb{E}\Big[\overline{P}_{0}^{U}\Big]$
,
$\mathbb{E}\Big[\overline{P}_{0}^{U}\Big]$
,
![]() $\mu^{U}$
,
$\mu^{U}$
,
![]() $\tilde{\mu}^{U}$
, and
$\tilde{\mu}^{U}$
, and
![]() $\tilde{A}^{U}$
, respectively. Notice that
$\tilde{A}^{U}$
, respectively. Notice that
 \begin{align*} V_{n,1}^{U} &\;:\!=\; \frac{1}{\tilde{C}_{n}^{U}} \sum_{j=1}^{n} \biggl( \frac{Z_{j}-I_{j-1}^{U}}{Z_{j-1}} - M_{n}^{U} \biggr)^{2} \tilde{\chi}_{j-1}^{U} \quad \text{ and } \\[5pt] V_{n,2}^{U} &\;:\!=\; \frac{1}{\tilde{C}_{n}^{U}} \sum_{j=1}^{n} \frac{1}{Z_{j-1}} \sum_{i=1}^{Z_{j-1}} \biggl( \xi_{j-1,i}^{U} - \frac{Z_{j}-I_{j-1}^{U}}{Z_{j-1}} \biggr)^{2} \tilde{\chi}_{j-1}^{U}\end{align*}
\begin{align*} V_{n,1}^{U} &\;:\!=\; \frac{1}{\tilde{C}_{n}^{U}} \sum_{j=1}^{n} \biggl( \frac{Z_{j}-I_{j-1}^{U}}{Z_{j-1}} - M_{n}^{U} \biggr)^{2} \tilde{\chi}_{j-1}^{U} \quad \text{ and } \\[5pt] V_{n,2}^{U} &\;:\!=\; \frac{1}{\tilde{C}_{n}^{U}} \sum_{j=1}^{n} \frac{1}{Z_{j-1}} \sum_{i=1}^{Z_{j-1}} \biggl( \xi_{j-1,i}^{U} - \frac{Z_{j}-I_{j-1}^{U}}{Z_{j-1}} \biggr)^{2} \tilde{\chi}_{j-1}^{U}\end{align*}
are used to estimate
![]() $V_{1}^{U}$
and
$V_{1}^{U}$
and
![]() $V_{2}^{U}$
. As in the proof of Theorem 2.4, it is easy to see that
$V_{2}^{U}$
. As in the proof of Theorem 2.4, it is easy to see that
![]() $V_{n,1}^{U}$
and
$V_{n,1}^{U}$
and
![]() $V_{n,2}^{U}$
are consistent estimators of
$V_{n,2}^{U}$
are consistent estimators of
![]() $V_{1}^{U}$
and
$V_{1}^{U}$
and
![]() $V_{2}^{U}$
. Similar comments hold when U is replaced by L.
$V_{2}^{U}$
. Similar comments hold when U is replaced by L.

Using the above estimators in Theorem 2.6, we obtain the following confidence intervals for
![]() $M_{n}^{U}$
and
$M_{n}^{U}$
and
![]() $M_{n}^{L}$
. We also provide confidence intervals for the estimator
$M_{n}^{L}$
. We also provide confidence intervals for the estimator
![]() $M_{n}$
defined below, which does not take into account different regimes. Specifically,
$M_{n}$
defined below, which does not take into account different regimes. Specifically,
 \begin{equation*} M_{n} \;:\!=\; \frac{1}{\sum_{j=1}^{n} \textbf{I}_{\{Z_{j-1} \geq 1\}}} \sum_{j=1}^{n} \frac{Z_{j}-I_{j-1}^{T}}{Z_{j-1}} \textbf{I}_{\{Z_{j-1} \geq 1\}},\end{equation*}
\begin{equation*} M_{n} \;:\!=\; \frac{1}{\sum_{j=1}^{n} \textbf{I}_{\{Z_{j-1} \geq 1\}}} \sum_{j=1}^{n} \frac{Z_{j}-I_{j-1}^{T}}{Z_{j-1}} \textbf{I}_{\{Z_{j-1} \geq 1\}},\end{equation*}
where
![]() $I_{j-1}^{T}$
is equal to
$I_{j-1}^{T}$
is equal to
![]() $I_{j-1}^{U}$
if
$I_{j-1}^{U}$
if
![]() $T=U$
and 0 otherwise.
$T=U$
and 0 otherwise.


Figure 2. The four columns give the results of the numerical experiments 1, 2, 3, and 4. The first row shows the process
![]() $Z_{n}$
for
$Z_{n}$
for
![]() $n=10^4-10^2, \dots, 10^4$
. The second and third rows show the empirical probability distributions of
$n=10^4-10^2, \dots, 10^4$
. The second and third rows show the empirical probability distributions of
![]() $\big\{ \Delta_{j}^{L} \big\}$
and
$\big\{ \Delta_{j}^{L} \big\}$
and
![]() $\big\{ \Delta_{j}^{U} \big\}$
, respectively.
$\big\{ \Delta_{j}^{U} \big\}$
, respectively.
Next, we investigate the behavior of the process when the thresholds
![]() $L_{j}$
and
$L_{j}$
and
![]() $U_{j}$
increase with j. To this end, we let
$U_{j}$
increase with j. To this end, we let
![]() $L_{0}=10^{2}$
,
$L_{0}=10^{2}$
,
![]() $L_{U}=10^{4}$
, and
$L_{U}=10^{4}$
, and
![]() $n \in \{0,1, \dots, 10^3\}$
and take initial distribution
$n \in \{0,1, \dots, 10^3\}$
and take initial distribution
![]() $Z_{0}$
, immigration distribution
$Z_{0}$
, immigration distribution
![]() $I_{0}^{U}$
, and offspring distributions
$I_{0}^{U}$
, and offspring distributions
![]() $\xi_{0,1}^{U}$
and
$\xi_{0,1}^{U}$
and
![]() $\xi_{0,1}^{L}$
as in Experiment 1. We consider four different distributions for
$\xi_{0,1}^{L}$
as in Experiment 1. We consider four different distributions for
![]() $L_{j}$
and
$L_{j}$
and
![]() $U_{j}$
, as follows:
$U_{j}$
, as follows:

The results of Experiments 5–8 are shown in Figure 3. From the plots, we see that the number of cases after crossing the upper thresholds is between
![]() $10^{4}$
and
$10^{4}$
and
![]() $2 \cdot 10^{4}$
, whereas when the thresholds increase they almost reach the
$2 \cdot 10^{4}$
, whereas when the thresholds increase they almost reach the
![]() $6 \cdot 10^{4}$
mark. Also, the number of regimes up to time
$6 \cdot 10^{4}$
mark. Also, the number of regimes up to time
![]() $n=10^3$
decreases, as it takes more time to reach a larger threshold. As a consequence, the overall number of cases also increases.
$n=10^3$
decreases, as it takes more time to reach a larger threshold. As a consequence, the overall number of cases also increases.

Figure 3. From left to right, Experiments 5, 6, 7, and 8. The process
![]() $Z_{n}$
for
$Z_{n}$
for
![]() $n \in \{0,1,\dots,10^{3} \}$
(in black), horizontal lines at
$n \in \{0,1,\dots,10^{3} \}$
(in black), horizontal lines at
![]() $L_{0}$
and
$L_{0}$
and
![]() $L_{U}$
(in red), and the thresholds
$L_{U}$
(in red), and the thresholds
![]() $U_{j}$
and
$U_{j}$
and
![]() $L_{j}$
(in blue).
$L_{j}$
(in blue).
Acknowledgements
The authors thank an anonymous reviewer for careful reading of the manuscript and for suggesting additional references.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.