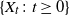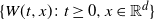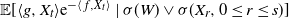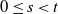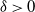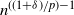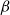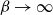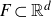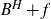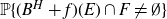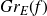1685 results in 60Jxx
Some conditional properties of superprocesses in random environments
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1-17
-
- Article
- Export citation
The real-time growth rate of stochastic epidemics on random intersection graphs
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perturbation theory for killed Markov processes and quasi-stationary distributions
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 19 March 2025, pp. 1-28
-
- Article
- Export citation
The speed of a biased walk on a Galton–Watson tree without leaves is monotonic for low values of bias
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 05 March 2025, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
Phase-type representations for exponential distributions
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-31
-
- Article
- Export citation
A non-convex optimization approach of searching algebraic degree phase-type representations for general phase-type distributions
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1-37
-
- Article
- Export citation
Long edges in Galton–Watson trees
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 18 February 2025, pp. 1-16
-
- Article
- Export citation
Optimal convergence rates of MCMC integration for functions with unbounded second moment
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Critical configurations of the hard-core model on square grid graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 04 February 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The number of individuals alive in a branching process given only times of deaths
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 31 January 2025, pp. 1-36
-
- Article
- Export citation
Asymptotic expansion of the invariant measure for Markov-modulated ODEs at high frequency
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 30 January 2025, pp. 1-27
-
- Article
- Export citation
Perturbation analysis of Markov chain Monte Carlo for graphical models
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 06 January 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mean-field analysis of stochastic networks with reservation
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 06 January 2025, pp. 1-27
-
- Article
- Export citation
Fractional Brownian motion with deterministic drift: how critical is drift regularity in hitting probabilities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 February 2025, pp. 103-132
- Print publication:
- January 2025
-
- Article
- Export citation
The Markov chain embedding problem in a one-jump setting
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
Sampling from the random cluster model on random regular graphs at all temperatures via Glauber dynamics
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-33
-
- Article
-
- You have access
- HTML
- Export citation
Optimal stopping of Gauss–Markov bridges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 04 December 2024, pp. 1-34
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Discounted optimal stopping zero-sum games in diffusion type models with maxima and minima
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 241-270
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Brownian range and the Brownian reversal
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence of the derivative martingale for the branching random walk in time-inhomogeneous random environment
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-35
-
- Article
-
- You have access
- HTML
- Export citation