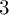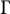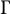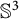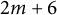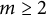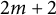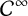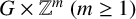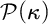242 results in 57Mxx
Graph morphisms and exhaustion of curve graphs of low-genus surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1-51
-
- Article
- Export citation
All, most, some? On diffeomorphisms of the interval that are distorted and/or conjugate to powers of themselves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-36
-
- Article
- Export citation
STATED SKEIN MODULES OF 3-MANIFOLDS AND TQFT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 19 March 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fiber bundles associated with Anosov representations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 March 2025, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generating the liftable mapping class groups of regular cyclic covers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-20
-
- Article
- Export citation
Ample Groupoids, Topological Full groups, Algebraic K-theory Spectra and Infinite Loop Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum to ‘From Curves to Currents’
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 29 January 2025, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large N limit of the Yang–Mills measure on compact surfaces II: Makeenko–Migdal equations and the planar master field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 January 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete group actions on 3-manifolds and embeddable Cayley complexes
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 January 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The coarse geometry of hexagon decomposition graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite presentability of twisted Brin–Thompson groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poncelet’s closure theorem and the embedded topology of conic-line arrangements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 109-123
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Equivariant covering type and the number of vertices in equivariant triangulations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
Period realization of meromorphic differentials with prescribed invariants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 November 2024, e90
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REIDEMEISTER’S THEOREM USING TRANSVERSALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 356-367
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
A NOTE ON THE FINITELY GENERATED FIXED SUBGROUP PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1-11
-
- Article
-
- You have access
- HTML
- Export citation
EXCEPTIONAL SIMPLE REAL LIE ALGEBRAS
 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND  $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 July 2024, pp. 157-201
- Print publication:
- January 2025
-
- Article
-
- You have access
- HTML
- Export citation
From real-life to very strong axioms. Classification problems in Descriptive Set Theory and regularity properties in Generalized Descriptive Set Theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 November 2024, pp. 285-286
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Adjoint Reidemeister torsions of some 3-manifolds obtained by Dehn surgeries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 887-901
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Singer conjecture for varieties with semismall Albanese map and residually finite fundamental group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation