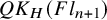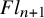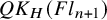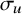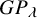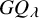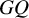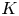171 results in 14Mxx
Rationality and arithmetic of the moduli of abelian varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOTT MANIFOLDS WITH VANISHING FUTAKI INVARIANTS FOR ALL KAHLER CLASSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-20
-
- Article
- Export citation
Coordinate rings of regular nilpotent Hessenberg varieties in the open opposite schubert cell
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 February 2025, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometrization of the Satake transform for mod p Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 February 2025, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A presentation of the torus-equivariant quantum K-theory ring of flag manifolds of type A, Part II: quantum double Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Casimir operators for loop Lie superalgebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-17
-
- Article
- Export citation
Generic stabilizers for simple algebraic groups acting on orthogonal and symplectic Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 ${\mathbb {Q}}$-FANO THREEFOLDS AND LAURENT INVERSION
${\mathbb {Q}}$-FANO THREEFOLDS AND LAURENT INVERSION
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1-47
-
- Article
- Export citation
TWO NON-VANISHING RESULTS CONCERNING THE ANTI-CANONICAL BUNDLE
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4-Torsion classes in the integral cohomology of oriented Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 January 2025, pp. 1-43
-
- Article
- Export citation
A new generic vanishing theorem on homogeneous varieties and the positivity conjecture for triple intersections of Schubert cells
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-12
- Print publication:
- January 2025
-
- Article
- Export citation
An inverse Grassmannian Littlewood–Richardson rule and extensions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 03 December 2024, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Resolutions of toric subvarieties by line bundles and applications
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 November 2024, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semistable degenerations of Calabi–Yau manifolds and mirror P=W conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 November 2024, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special homogeneous surfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 22 October 2024, pp. 333-362
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
A short proof of the Hanlon-Hicks-Lazarev Theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Combinatorial formulas for shifted dual stable Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 February 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Δ–Springer varieties and Hall–Littlewood polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 31 January 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Manin–Peyre conjecture for smooth spherical Fano varieties of semisimple rank one
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 January 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Grothendieck–Serre conjecture over valuation rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 317-355
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation