Introduction
For the next century, glaciers and ice caps are expected to make a major contribution to sea-level rise due to global warming. The models used to make the estimates for the Intergovernmental Panel on Climate Change (IPCC) Second Assessment Report (Reference Warrick, le Provost, Meier, Oerlemans, Woodworth, Houghton, Meira Filho, Callander, Harris, Kattenberg and MaskellWarrick and others, 1996) have shortcomings. One set of estimates was based on a heuristic glacier model (Reference Wigley and RaperWigley and Raper, 1995) which kept account of the diminishing glacier volume but used globally uniform annual temperature change as the climate forcing. Another analysis included temperature changes differentiated by season and latitude, but considered only the mass balance and not the glacier dynamics (Reference DeWolde, Huybrechts, Oerlemans and van de Walde Wolde and others, 1997). More recently this analysis has been extended to include regional temperature changes (Reference Gregory and OerlemansGregory and Oerlemans, 1998).
To capture the effect of climate forcing and glacier dynamics, estimates of glacier melt need to be based on mass balance that is coupled to dynamic models and applied regionally. Such models have been applied, for example, to 12 individual glaciers for hypothetical forcing scenarios (Reference OerlemansOerlemans and others, 1998). However, the application of such detailed models on a global basis appears to be impractical and inappropriate given the uncertainty in the global distribution of glacier areas and thickness (Reference Meier and BahrMeier and Bahr, 1996).
In several recent papers, scaling methods have been developed, based on theoretical considerations and observations, to give a physically based and practical method for estimating ice area, thickness and hence volume (Reference Meier and BahrMeier and Bahr, 1996; Reference BahrBahr, 1997; Reference Bahr, Meier and PeckhamBahr and others, 1997). For the purposes of estimating global glacier melt it therefore seems entirely appropriate to develop a glacier model with implicit dynamics using the same scaling methods. Such a geometric model was developed by Reference Raper, Briffa and WigleyRaper and others (1996). Building on this work, we describe below how we have coupled a mass-balance degree-day model to the simple geometric model. As a case-study we apply the model to Hintereisferner, Austrian Alps, and compare the results with those of a dynamic model (Reference GreuellGreuell, 1989, Reference Greuell1992). We then show a series of sensitivity studies that demonstrate the ability of the coupled model to reproduce the expected response of different glacier shapes to a climate change.
Model Description
The purpose of the model is to calculate changing glacier volume with time, so we start with the usual requirement that the change in glacier volume (V) with time (t) is equal to the area-averaged net mass balance (mean specific balance) multiplied by the surface area of the glacier,
where 〈b〉 t is the mean specific balance and St is the annual mean surface area (m2). According to the standard definition, the mean specific balance is given by:

where bt , i is the specific balance at time t in the ith elevation band on the glacier with an area of st , i . Equations (1) and (2) show that in order to calculate the changing glacier volume it is necessary to calculate the time evolution of the altitudinal distribution of the glacier mass balance and area. For the former we use a mass-balance degree-day model and for the latter a simple geometric glacier model which is a development from Reference Raper, Briffa and WigleyRaper and others (1996).
The mass balance is calculated with the degree-day model (Reference BraithwaiteBraithwaite, 1980, Reference Braithwaite1985; Reference Braithwaite, Olesen and OerlemansBraithwaite and Olesen, 1989; Reference Huybrechts, Letréguilly and ReehHuybrechts and others, 1991; Reference ReehReeh, 1991; Reference JóhannessonJóhannesson, 1997; Reference Braithwaite and ZhangBraithwaite and Zhang, 2000). According to this model the balance at ith elevation is given by:
where ct , i is the annual accumulation of snow, mt , i is the annual melt and rt , i is the annual refreezing at time t, in the ith elevation band.
The accumulation for each month is calculated from monthly precipitation by taking account of the probability of below-freezing temperatures as a function of monthly mean temperatures (Reference BraithwaiteBraithwaite, 1985).
The monthly melt is assumed proportional to the positive degree-day sum that is also calculated from monthly mean temperature (Reference BraithwaiteBraithwaite, 1985). The proportionality factors (positive degree-day factors), linking melt to positive degree-day sum, depend upon whether the melting refers to ice or snow. There is a wide range of values in the literature (Reference Braithwaite and ZhangBraithwaite and Zhang, 2000), but typical degree-day factors for ice and snow are 8.0 and 4.5 mm d−1°C−1, respectively.
The refreezing is estimated for subpolar glaciers by assuming that all annual melt is refrozen within the snow cover, thereby increasing the snow density, and that runoff occurs only if the surface density reaches the density of glacier ice (890 kg m−3). This occurs when the annual melt amounts to 0.58 times the annual accumulation, assuming an initial snow density of 375 kg m−3 (Reference Braithwaite, Laternser and PfefferBraithwaite and others, 1994), at the runoff line on a subpolar glacier. The mass balance below the runoff line is given by:
The monthly temperature and precipitation are extrapolated to the altitude in question from a nearby weather station or from a suitable gridded climatology (e.g. Reference New, Hulme and JonesNew and others, 1999). The precipitation distribution with altitude is tuned so that the modelled distribution of mass balance with altitude agrees with the field data. The precipitation obtained by this tuning is the effective precipitation over the glacier, which is often higher than the precipitation value available in a gridded climatology, or read off a weather map.
The geometric model predetermines the altitudinal distribution of the glacier area for any volume. We therefore assume a steady-state glacier shape at all times, thus eliminating the need for explicitly considering the ice dynamics. The implications of this assumption are considered later in the paper. The model equations involve scaling factors for relating glacier area to volume, and width to length. Such scaling factors have recently been investigated using World Glacier Inventory data and the partial differential equations describing glacier dynamics (Reference BahrBahr, 1997; Reference Bahr, Meier and PeckhamBahr and others, 1997). After determining the change in the volume from Equations (1–4), the time evolution of glacier area and width and length are determined from
and
where St ,Vt , Wt and Lt are the glacier area, volume, mean width and maximum length, respectively, at time t. Subscript “R” represents the present or reference value. Equation (5) also determines the evolution of the mean glacier depth, and Equation (6) multiplied by (Lt /L R) gives
so that the length can be calculated directly from the area.
A simplified reference altitude distribution of the glacier area is defined based on observed glacier data. Next, assumptions need to be made as to how the altitude distribution changes with a changing area. Take, for example, a glacier that has a triangular shape that decreases linearly in width from the top to a width of zero at the terminus. Assuming a fixed altitude for the top, then for different areas the altitude of the terminus can be calculated from Equation (7) assuming a constant ratio of the altitudinal range to the glacier length. Assuming the width decreases linearly from the top to the terminus for all areas, the area–altitude distribution is defined for all areas. Using suitable elevation-band width intervals, the area–altitude information for the area at each time-step is used in the calculation of the mass balance over the glacier at the next time-step.
The assumption of steady-state shape made for the geometric model means, for example, that the model does not wholly take account of the mass-balance–elevation feedback. It does account for that part of the feedback associated with changes in the mean depth. It does not, however, account for the delayed response of the ice dynamics whereby an increase (decrease) in ablation or accumulation will initially increase (decrease) the slope of the glacier surface. Similarly, a glacier surge and recovery will affect the glacier slope. Thus the geometric model assumes the shape of the glacier for any volume is the same irrespective of whether it is in advance or retreat, whereas in reality this is not strictly the case. It is therefore necessary to assess the importance of this assumption by comparing the results of this model with models that more explicitly consider the ice dynamics. Towards this aim we have undertaken a case-study which we present below.
Application to Hintereisferner
Model calibration
We have applied the coupled model to Hintereisferner, a valley glacier in the Austrian Alps (46°50′ N, 10°50′ E). We consider both the main stream and the subsidiary Langtaufererjochferner. We do not consider Kesselwandferner, even though there is evidence that it was joined to Hintereisferner on several occasions over the last century (Reference GreuellGreuell, 1989).
The evaluation of the parameters used in the coupled model is described below and the values are given in Table 1. For the climate data we use monthly mean temperature and precipitation, averaged over 1961–90 from Vent (46°50′ N, 10°56′ E; 16 km southwest of Hintereisferner). The assumed degree-day factors for snow and ice are 4.5 and 8.0 mm d−1oC−1. The mass-balance model is calibrated to fit the mean 1961–90 observed mass-balance profile. As the precipitation over the glacier is not well known it is treated as a tuning parameter and varied to make the model fit the observed data. The mean 1961–90 seasonal distribution of precipitation in terms of monthly means is assumed to be the same as that at Vent. The vertical lapse of temperature is assumed to have a seasonal cycle that is estimated from Vent and Innsbruck 1961–90 monthly mean station data and has a maximum value of 0.7°C per 100 m in April and a minimum of 0.3°C per 100 m in December. The resulting modelled and observed mass-balance profiles are shown in Figure 1a, and the assumed annual mean precipitation profile is given in Table 2.

Fig. 1 The coupled mass-balance geometric model applied to Hintereisferner. (a) Mean 1961–90 mass-balance profile: observed (boxes), fitted model (solid line) and modelled perturbation for a 1°C warming (dashed line) (b) Modelled mass-balance series corresponding to the central estimate of the reference glacier depth (thin line) and the observed mass-balance series (thick line). (c) Reconstructed volumes, 1892–1996, for the high (×), mid- (−) and low (◆) reference depth cases. Also shown in (c) are the volume changes corresponding to the observed mass-balance data used with the modelled area changes (thick line). (d) Same as (c) but for areas.
Table 1. Parameter values for the coupled model applied to Hintereisferner

Table 2. Altitudinal distribution of annual mean precipitation for tuned Hintereisferner mass-balance model
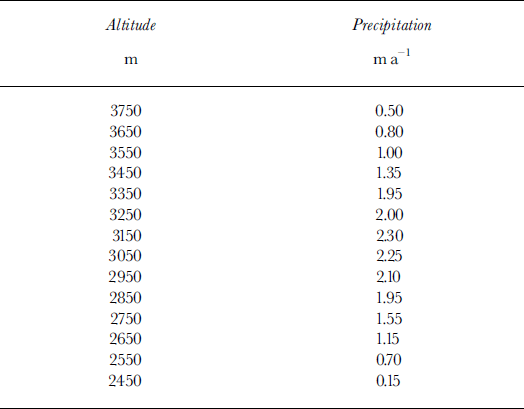
The 1990 area–altitude distribution of Hintereisferner is shown in Figure 2. For the geometric model calculations, we need to define a reference altitude distribution of the glacier area which approximates the real distribution. It is simplest if this distribution is a single simple function. Here we choose a linear increase in the area distribution function with altitude, as shown in Figure 2. Using this linear function, the total area equals the total observed area when the height of the top is specified as 3291 m. Thus we treat that part of the real area which lies above 3291 m as if it lies between 3125 and 3291 m. Since the mass balance above 3125 m does not vary much with altitude, this assumption is reasonable (see Fig. 1a). The fixed height of the top of the glacier in the geometric model is thus specified as 3291 m.

Fig. 2. The 1990 area–altitude distribution of Hintereisferner (solid line) and the assumed distribution for modelling purposes (dashed line).
For the geometric model reference area, S R, we use the 1990 area of 9.0 km2. As a central estimate of the mean depth we use a value of 65 m based on Reference GreuellGreuell (1989, fig. 3.3) and Reference OerlemansOerlemans and others (1998, table 1) and compatible with Reference Bahr, Meier and PeckhamBahr and others (1997, fig. 1). We show that modelled areas for the past are very sensitive to uncertainty in the mean depth. We use a low and high estimate of the mean depth of 52 and 78 m, respectively, this being an uncertainty range of ±20%. With reference to Reference GreuellGreuell (1989) this represents an uncertainty of a factor of 4 in the flow parameters. The resulting three alternative reference volumes are given in Table 1. For the reference length, L R, we use the 1990 value of 7.2 km, which results in a mean width, W R, of 1.25 km. For the parameters, γ and q, we use values of 1.36 and 0.6, respectively, as suggested by Reference BahrBahr (1997) and Reference Bahr, Meier and PeckhamBahr and others (1997) based on analysis of glacier inventory data. We thus assume that shape characteristics from a sample of different glaciers at one time are applicable to one glacier at different times. We show in a subsequent section that the volume-response time of the glacier model is sensitive to the chosen values for the parameters γ and q. In support of the values used here, the averages of the modelled volume e-folding times for a positive and negative mass-balance perturbation from 1990, for the three depths considered, range from 67 to 95 years. This is in excellent agreement with the range of 64–96 years given by Reference GreuellGreuell (1989, table 2) obtained for a factor of 4 uncertainty in the flow parameters. Assuming that a glacier is in equilibrium, Reference JóhannessonJóhannesson (1997) shows that the volume-response time can be estimated as the maximum thickness divided by the mass balance at the terminus. Since Hintereisferner is presently in retreat, the large negative values of the mass balance at the terminus give estimates of the response time about four times less than those quoted above (assuming the maximum thickness is equal to the mean thickness divided by 0.6).
Reconstruction of volume and area from 1892
For the climate forcing we use reconstructed monthly mean temperature and precipitation data from Vent available from 1891 to 1996. Systematic temperature and precipitation records were kept for Vent from 1934. Using pre-1934 intermittent data and neighbouring-station data, Reference LaufferLauffer (1966) reconstructed the records back to 1891 (temperature to 1851). Although a station move is recorded for precipitation in 1948, comparison with Marienberg (19 km southwest of Hintereisferner) annual precipitation does not indicate any systematic difference between the series (Reference Kuhn, Schlosser and SpanKuhn and others, 1997). However, the reliability of our reconstruction obviously depends on the reliability of the climate forcing.
To run the model with the climate forcing from Vent starting in 1891/92, it is necessary to specify the starting glacier volume. The starting area then follows from Equation (5). Alternative starting volumes and areas corresponding to the three reference depths are found iteratively. This is done by adjusting the starting volume until the modelled 1961–90 area-averaged mean mass balance coincides with the observed value. This results in the best possible coincidence of the observed and modelled mass-balance over 1961–90, the period over which the degree-day model was tuned to fit the mass-balance profile. The resulting reconstructed 1990 areas, 8.5, 8.6 and 8.8 km2, are, however, slightly smaller than the 1990 reference area of 9.0 km2. This is possibly due to the relatively large negative mass balances leading up to 1990 causing the modelled area to shrink too rapidly due to the steady-state shape assumption. As an alternative tuning strategy, the starting volumes could have been adjusted slightly upwards so that the 1990 volumes were coincident at 9.0 km2. The modelled mean 1961–90 mass balance would then have been slightly more negative than the observed.
Figure 1b shows the resulting modelled mass-balance series corresponding to the central estimate of the reference glacier depth together with the observed mass-balance series. Over the period of overlap the modelled and observed data agree well: the correlation coefficient is 0.87. The pre-1958 reconstructed mass-balance series is generally negative. The reconstructed mass-balance series depends on the value of the reference depth. For the low-depth case, the past glacier area is larger and the past mass balance is more negative. The opposite is true for the high-depth case (see below for a fuller explanation).
The reconstructed volumes and areas are shown in Figure 1c and d. For the mid-depth case we also plot the volume change corresponding to the observed mass-balance data used with the modelled area changes. Similar agreement is found for the other depth cases (not shown). Figure 1c shows that, despite the different reference volumes, the 1892 volumes are of similar magnitude. The volume results are summarized in Table 3a as 30 year means. Thus the relative change in volume from 1892–1921 to 1961–90 is larger for the low-depth case (45%) than for the high-depth case (27%). To help understand this difference, the corresponding 30 year mean equilibrium volumes are shown in parentheses. These were calculated by running the model forward from 1921 using constant 1892–1921 mean climate as the forcing. The low-depth case is more out of equilibrium in 1892–1921 than the high-depth case. For the low-depth case, 24% of the change from 1892–1921 to 1961–90 is due to this disequilibrium; the corresponding value for the high-depth case is only 6%.
Table 3. Volume and area results for the Hintereisferner modelling, summarized as 30 year means

The volume results are better understood with reference to the corresponding glacier area results given in Figure 1d and Table 3b. For 1892 there is a large difference in the modelled glacier areas. Since the different areas are subject to the same climate forcing, the equilibrium areas for 1892–1921 are similar. It follows that for the low-depth case the larger area is more out of equilibrium and the corresponding mass-balance is more negative than for the small-glacier-area case. The different 1892–1921 states (in terms of equilibrium) cause the larger volume and area change between 1892–1921 and 1961–90 for the low-depth than for the high-depth case.
We have shown above that part of the change from 1892–1921 to 1961–90 is due to climate change over the period, and part is due to 1892–1921 disequilibrium. We next assess how much the climate-driven changes are due to changes in temperature and how much they are due to changes in precipitation. To do this we have run the model for the three depth cases with constant 1892–1921 precipitation but with changing temperature. The results are summarized in Table 3 in the square brackets. The volume change for the low-depth case is then 39% and for the high-depth case 21%. For all three cases, about 15% of the change in volume was due to an increase in temperature, and 6% due to a decrease in precipitation.
The good agreement between the observed and modelled mass-balance series over 1953–95 confirm other reports of good results obtained with degree-day mass-balance models. Independent data are needed, however, to assess the performance of the geometric model. Historical glacier length data are available for Hintereisferner, but we do not use these data because we cannot expect the geometric model to make a good reconstruction of length on the decadal time-scale due to our steady-state-shape and uniform-slope assumptions. Our mid-estimate of a decrease in glacier volume of 40% from about 1892 to 1985 agrees with that of Reference GreuellGreuell (1992) using his best estimate for the flow parameters. We note that Greuell’s estimate uses a pre- 1948 precipitation reconstructed from a regional average giving a smaller precipitation decrease over the period. Since the volume change due to a change in precipitation in our reconstruction was only 6%, the different climate forcing is likely to have only a small effect. An independent glacier area estimate of 15.11 km2 in 1850 is recorded by Reference NicolussiNicolussi (1995). This appears to be compatible with our range of areas of 12–16 km2 for 1892, depending on the climate from 1850 to 1892. In addition, the reconstructed values for the 1990 area of 8.5–8.8 km are reasonably close to the observed area of 9.0 km2. For further verification we compare our results to those reported in Reference OerlemansOerlemans and others (1998) for Reference GreuellGreuell’s (1992) dynamic model using a future climate scenario.
Future change scenarios for Hintereisferner
The model response to the six climate change scenarios defined by Reference OerlemansOerlemans and others (1998) is investigated using the three alternative reference volumes given in Table 1. The forcing scenarios take the form of constant warming rates of 0.01, 0.02 and 0.04°Ca−1 imposed on the 1961–90 mean climate to represent possible climate change from 1990 to 2100. These warming rates are imposed, first, with constant 1961–90 precipitation and, second, with a change of precipitation of + 10% per °C warming. The scenarios are denoted 0.01, 0.02, 0.04, 0.01+, 0.02+ and 0.04+, respectively. The normalized volume results are shown in Figure 3a–c, and results for scenario 0.02 are summarized in terms of 30 year means in the last two columns of Table 3a and b.

Fig. 3. The Hintereisferner model results for six climate change scenarios for the high (×) mid- (−) and low (◆) reference depth cases: constant precipitation scenarios (thick line), change of precipitation of +10% per °C warming (thin line).
The future scenario cases differ from the historical cases described in the previous subsection because the 1961–90 starting areas were similar for the three reference depth cases, whereas the 1892–1921 starting areas were markedly different. Because the starting areas are virtually the same, the degree of disequilibrium is also similar. As a result, the volume change from 1961–2100 to 2071–2100 due to initial disequilibrium is proportionally similar for all three reference depth cases, in the 22–25% range. However, as in the historical case, the area change is greater for the low-depth than for the high-depth case. The proportional volume change is also greater for the low-depth case, 71% compared to 62% for the high-depth case, but bear in mind that because of the different starting volumes the actual volume change is greater for the high-depth case.
The normalized volume changes given in Figure 3b can be compared with those of Reference OerlemansOerlemans and others (1998). We note that differences could arise through differences in the treatment of the mass balance as well as the differences in the underlying glacier models. It is noticeable that in 2050 our model response for the mid-depth case is smaller than that shown by Reference OerlemansOerlemans and others (1998) by about 13% and 10% for scenarios 0.02 and 0.02+, respectively. By 2100 the differences have reduced to about 7% and 3%, respectively. The smaller volume response of our model is consistent with the slightly small starting (1990) volumes used. It is also consistent with our steady-state-shape assumption, whereby the area of the glacier responds immediately to changes in its volume instead of reacting to accumulated changes in the mass balance with a time lag that is related to the dynamics of the glacier. Note, however, that the response times of our model and Reference GreuellGreuell’s (1989) model, which was used in Reference OerlemansOerlemans and others (1998), are very similar.
In conclusion, our model as applied to Hintereisferner appears to give results that are similar to those of the Greuell model, and which are also compatible with the available geomorphological data.
Sensitivity Studies
There are a number of factors that affect the response of a glacier to climate change. These include the climatic regime and the glacier shape. For the purpose of the calculation of global glacier melt as a contribution to sea-level rise it is not possible to model every glacier in detail. A more practical approach is first to divide the world’s glaciers into glaciated regions (Reference Oerlemans and FortuinOerlemans and Fortuin, 1992), or a finer mesh of gridboxes, with different climatic regimes. Then, if for each region or gridbox appropriate distributions of glacier size and shape are defined, these may be modelled with the geometric model.
In this section, the aim is to use the geometric model to calculate the response of generalized glaciers of different shape to a climate change and to compare the results to those expected from the literature. We attempt to separate some of the factors which affect glacier response in order to study their effect in isolation. The first two factors we consider relate to glacier shape: (i) the area–altitude distribution and (ii) different glacier depths. The second two factors relate to the responses under different climatic conditions: (iii) different mass-balance gradients, and (iv) changes in temperature vs changes in precipitation.
The three hypothetical glacier shapes used to illustrate the results are shown in Figure 4 in terms of the altitude-area distributions for total areas of 5 and 10 km2. The first shape has a decreasing glacier width with decreasing altitude and is typical of many valley glaciers. For comparative purposes we choose for the second a uniform width implying a parallel-sided glacier. The third has an increasing glacier width with decreasing altitude such as is commonly found in some sectors of ice caps.

Fig. 4. Example of glacier shapes used for the sensitivity analyses, in terms of area–altitude distribution of glaciers with total areas of 5 km2 (heavy lines) and 10 km2 (light lines).
For the first two studies we assume an alpine-type climatic regime, which results in glaciers with a relatively large mass turnover. So that we can compare the response of glaciers of different shape in isolation, we adjust the precipitation at each altitude to give as nearly as possible a linear mass-balance profile with altitude. The precipitation profile used is given in Table 4. The resulting mass-balance profile is shown in Figure 5a. For the glaciers of different shape to be in equilibrium under this climatic regime they must reside at different altitudes. Also shown in Figure 5a are the relative altitudes of the top and bottom of the glaciers with the area–altitude distributions given in Figure 4 and with a total area of 10 km2.

Fig. 5. Sensitivity study showing the effect of different glacier shape assumptions on glacier response to a mass-balance perturbation. (a) Mass-balance profile representing an alpine climatic regime (solid line). The range of altitudes where the glaciers of different shape reside at equilibrium are shown: narrowing channel (◇), parallel-sided channel (■), widening channel (▲). Also shown is the perturbed mass-balance profile (−0.538 m w.e. a−1). (b) Mass-balance series for the glacier shapes as in (a) with parameter values as follows: for a narrowing channel (◇) γ = 1.36 with q = 0.0 (dashed line), 0.6 (solid line) and 1.0 (dotted line); for a parallel-sided channel (■) γ = 1.36 with q = 0.6; and for a widening channel (▲) γ = 1.36 (solid line) and 1.25 (dotted line) with q = 1.0. (c) Modelled volumes; lines as in (b). (d) Modelled areas; lines as in (b).
Table 4. Precipitation profiles used in the sensitivity analyses. The altitude is relative to the initial ELA

A temperature increase of 1°C results in an initial change in the mean specific mass balance for the glacier with a narrowing channel of −538 mm a−1 and for the glacier with a widening channel of −556 mm a −1. These are the static sensitivities of the glaciers to a 1°C temperature increase. For comparison purposes we wish to use a uniform mass-balance perturbation with altitude and we choose the value of −538 mm a−1 as shown in Figure 5a.
To compare the response of the three glacier shapes we run the model with the perturbed mass-balance profile until a new equilibrium is reached. For the glacier shape with a narrowing channel we use γ = 1.36 and three values of q, q = 0.0, 0.6 and 1.0, for comparison purposes. Reference BahrBahr (1997) and Reference Bahr, Meier and PeckhamBahr and others (1997) discuss the implications of different values of q. A value of q = 0.0 implies that the valley-glacier width does not change as the length changes. A value of q = 1.0 implies that the width scales with the length and is expected to be applicable for ice caps and ice sheets. These two values represent the extreme possible range for valley glaciers. Inventory data suggest a suitable value of q for valley glaciers is 0.6, and this is used here as an intermediate value. As stated earlier, the use of values derived from inventory data implies an assumption that shape characteristics from a sample of different glaciers at one time are applicable to one glacier at different times. A value of q = 0.6 is also used for the parallel-sided glacier example. The appropriate values for glaciers with widening channels, such as are found on ice caps, are thought to be γ = 1.25 and q = 1.0; for comparison we also use a value of γ of 1.36. The results are shown out to year 500 in Figure 5b–d and summarized in Table 5. We make a number of observations:
The response of a glacier with a narrowing channel is sensitive to the chosen value of q. Smaller q leads to a smaller change in the area and volume and shorter e-folding times.
The e-folding times are longer for the glaciers with a narrowing channel and shorter for the glaciers with a widening channel, in agreement with the analytic solution for the response time for a similar model given in Reference Raper, Briffa and WigleyRaper and others (1996) and the theory developed by Reference JóhannessonJóhannesson (1997).
The equilibrium volume and area change is larger for the glaciers with a narrowing channel than for the glacier with a widening channel.
As a result of the second and third points, at all times the response of the glaciers with a widening channel is less than the response of those with a narrowing channel.
This difference is small for q = 0 but increases for larger values of q. The proportional differences between the areas and volumes increases with time until equilibrium is reached.
Table 5. Initial and equilibrium volumes and areas, and the e-folding times and volume-response times which summarize the results shown in Figures 5–8

In conclusion, according to the geometric model results, under the same climatic conditions glaciers with a narrowing channel change more with a change in mass balance due to their shape and the way in which that shape changes with a changing climate compared to glaciers with a widening channel. The degree of difference in behaviour, however, is very sensitive to the chosen value of q.
Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others (1989) have shown that the volume-response time of glaciers, τ v, can be estimated as τ v = h/(−b T), where h is the thickness scale for the glacier and b T is the balance rate at the terminus. In Table 5 we compare the volume e-folding times obtained for the negative mass-balance perturbation with this volume-response time. The thickness scale is assumed to be the mean depth divided by 0.6. Note that Jóhannesson’s response time is applicable to a small perturbation to a glacier in equilibrium, whereas the e-folding times given in Table 5 are for a substantial negative mass-balance perturbation. The e-folding times for a similar but positive mass-balance perturbation, which results in glacier growth, are longer by a factor of about 1.5.
Taking into account the above considerations, our e-folding times agree quite well with the response times given by Jóhannesson’s formula in the case of the ice caps. However, Jóhannesson’s formula gives shorter response times for glaciers with a narrowing channel than for ice caps, whereas our e-folding times are longer for glaciers with a narrowing channel than for ice caps. For glaciers with a narrowing channel the formula gives shorter response times because the terminus extends to lower altitudes (giving larger b T), whereas the e-folding times are longer because the area and volume changes are bigger, depending on the chosen value of q.
In the next sensitivity study, we investigate the effect of the glacier thickness on the volume-response time in our model. Then, in the third sensitivity study, we investigate the effect of a different mass-balance rate at the terminus.
To find the effect of mean depth, we run the model for two glacier shapes and sizes with the same climate forcing as used in the previous experiment. Based on the work of Reference BahrBahr (1997) and Reference Bahr, Meier and PeckhamBahr and others (1997), for an area of 10 km2 (as used in Figure 5) it is reasonable for valley-type glaciers and ice caps to have a similar mean depth, namely, the 100 m we used in the example. However, since the appropriate value of γ for valley-type glaciers is 1.36 and for ice caps is 1.25, the appropriate depths and volumes are significantly different for an area of 100 km2. We therefore compare the response of a glacier with narrowing channel of relatively small area and depth (10 km2 and 100 m) with a similar-shaped but larger glacier (100 km2 and 240 m) using for both γ = 1.36 and q = 0.6. We also compare two sizes of a glacier with a widening channel; we use for the larger glacier an area of 100 km2 and depth of 170 m, with for both sizes γ = 1.25 and i = 1.0. The initial altitudinal ranges of the glaciers of different shape are shown in Figure 6a. The ranges are the same for both sizes so that the mass balance at the terminus is initially the same.

Fig. 6. Sensitivity study showing the effect of different glacier depths on glacier response to a mass-balance perturbation: small glaciers (solid line); large glaciers (dashed line); narrowing channel with (◆) γ = 1.36 and q = 0.6; widening channel with (▲) γ = 1.25 and q = 1.0. (a) Mass-balance profiles; (b) mass-balance series; (c) modelled volumes; (d) modelled areas.
Figure 6c and d show the normalized volume and area response, respectively, and as expected from the above response-time formula for τ v, the response time of the larger glaciers with greater depth is longer (see Table 5). Thus the normalized volume change over the first few centuries is less for the deeper glaciers. In addition, also as expected from the results of Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others (1989), the normalized equilibrium volume and area changes are unaffected by the depth, or in other words, the equilibrium volume change is proportional to the mean thickness of the glacier. The e-folding times obtained for the ice-cap cases are in accord with the response-time formula. However, as before, those obtained for the glaciers with a narrowing channel and q = 0.6 are longer than given by the formula.
In order to investigate the effect of a different climatic regime, we choose a continental-type climate that results in glaciers with a relatively small mass turnover and thus a low mass balance at the terminus. To obtain such a climate we decrease the temperature by 5°C compared to that used previously (alternatively the altitude could be increased accordingly). In addition, under this colder climate we consider refreezing in the mass-balance model. As before, we adjusted the precipitation at each altitude to give as near as possible a linear mass-balance profile with altitude, and the values are given in Table 4. The resulting mass-balance profile is shown in Figure 7a. Also shown in Figure 7a are the relative altitudes of the top and bottom of the glaciers with different area-altitude distribution for total areas of 10 km2.

Fig. 7 As in Figure 5 but with a continental-type climate regime.
A temperature increase of 1°C from this continental climate results in an initial change in the mean specific balance for the glacier with a narrowing channel of −181 mm a−1 and for the glacier with a widening channel of −180 mm a−1. These two static sensitivities are almost the same because of the small mass-balance gradient, and in agreement with the findings of Reference Oerlemans and FortuinOerlemans and Fortuin (1992) and Braithwaite and Zhang (in press) they are much smaller than the sensitivities found for the alpine-type mass-balance profile discussed above.
To compare the response of the three glacier shapes under this climate, we perturb the mass-balance profile by a uniform value of −181 mm−1 and run the model to a new equilibrium. The results are presented in Figure 7 and should be compared with those of the first sensitivity study given in Figure 5. We make the following observations:
The relative modelled responses of the different glacier shapes and parameter values are the same as in the first analysis with the alpine climate.
The e-folding times for the glaciers under the continental climate conditions are much longer than those found for the alpine glaciers (see Table 5). This result is in agreement with the dependence of the response time on the mass balance at the terminus (Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others, 1989).
Despite the much smaller initial or static sensitivity, the equilibrium volume and area change for the continental glaciers is greater than the equilibrium change for the alpine glacier (see Table 5).
As a result of the above three items, over the first two and a half centuries the response of the glaciers under a continental climate is less than that of the glaciers under an alpine climate. However, by the beginning of the third century the response of the ice cap under the continental climate exceeds that of the one under an alpine climate. The crossover for valley-type glaciers is delayed.
In conclusion, the smaller static sensitivity and the longer response time of glaciers under a continental climate results in smaller volume and area changes over the first few centuries, the timing depending on the glacier shape. However, despite the smaller static sensitivity of glaciers under a continental climate, the equilibrium volume change of these glaciers is greater than that of the equivalent glaciers under an alpine climate.
Comparison of the response times given by Jóhannesson’s formula with the e-folding times given by our model under continental climate conditions leads to similar conclusions to those obtained for an alpine climate. Thus the results for glaciers with a widening channel are approximately in accord since the e-folding time is for a negative mass-balance perturbation. Also as before, the formula gives shorter response times for glaciers with a narrowing channel than for those with a widening channel, whereas the relative e-folding times are longer because of the greater changes in area and volume.
To conclude our sensitivity analyses we compare the model response to a step increase in temperature of 1°C and the equivalent change (in terms of change in mean specific balance) in precipitation. The differences in response are dependent on the climate regime. For the alpine-type climate in Table 4, where precipitation increases with altitude, the change in precipitation equivalent to an increase in temperature of 1°C is –35% for the glaciers both with a narrowing channel and with a widening channel. The reason the result is the same for both shapes is that, in this case, the different altitudes at which the glaciers reside at equilibrium balance the effect of the different balance perturbations and areas with altitude. The mass-balance altitude profiles resulting from these changes, together with an equivalent uniform-change profile, are shown in Figure 8a.

Fig. 8. Sensitivity study showing the effect of changes in temperature vs changes in precipitation. (a) Mass-balance profile for the alpine climate and for +1°C (×), for –35% precipitation (○) and for a uniform perturbation of −0.538 m w.e. a−1. Response of mass-balance perturbations in (a) on a valley-type glacier with γ = 1.36 and q = 0.6: (b) mass-balance series, (c) modelled volumes, (d) modelled areas.
The responses of a valley-type glacier to the different mass-balance perturbations given in Figure 8a are shown in Figure 8b–d. The volume and area equilibrium responses for the precipitation change are greater than those for the temperature change, but the differences in response are small compared with the other factors we have considered above. The smaller mass-balance perturbation at low altitude for the precipitation change means that the area has to shrink up further to restore equilibrium. Thus, to obtain the same equilibrium change in area as that caused by a 1°C temperature increase, the required change in precipitation is less than −35%.
The relative responses, to a change in temperature vs precipitation, of an ice-cap type glacier with the alpine climate regime are very similar to those shown in Figure 8. For the continental climate regime (see Table 4), the differences in the response to the different forcings are much reduced. Because of the steady-state assumptions made in our model, the response times to the different forcing profiles will in reality differ from those given here, but the equilibrium values should not be affected.
Conclusions
A mass-balance degree-day model has been coupled to a geometric glacier model for the estimation of glacier volume response to climate change. The ice dynamics are treated implicitly in the geometric model by using scaling parameters. These scaling parameters have been extensively investigated by Reference BahrBahr (1997) and Reference Bahr, Meier and PeckhamBahr and others (1997). Since the scaling parameters are based on the glacier inventory data and also on a theoretical analysis of glacier dynamics, the geometric model may be expected to reproduce results in accord with the dynamic theory. We have tested this by presenting a case-study of Hintereisferner and by extensive sensitivity studies.
Using climate data for Vent from 1892 we have reconstructed the past volume and area of Hintereisferner. We find the results are sensitive to the reference glacier depth. The range of 1892 area estimates of 12.0–15.7 km2 is compatible with an 1850 area of 15 km2. Our mid-estimate of a 40% decrease in the volume from 1892 to 1985 agrees well with that of Reference GreuellGreuell (1992), as also do our response times. Reasonably good agreement is also found with the results of Reference OerlemansOerlemans and others (1998) in which Greuell’s model was run with future climate change scenarios. The slightly slower response of our model is consistent with our steady-state shape assumption. For the 0.02°Ca−1 warming scenario, including the possibility of an increase in precipitation, we estimate the 2100 volume of Hintereisferner to be in the range 20–42% of its 1990 value.
We have investigated generalized glacier response to a mass-balance perturbation equivalent to a 1°C increase in temperature. Under the same climatic conditions, glaciers with a narrowing channel change more with a change in mass balance than glaciers with a widening channel, due to their shape and the way in which that shape changes with a changing climate. This result is very sensitive to the chosen value of the width-scaling parameter q. For values of q > 0.0, our response times for glaciers with a narrowing channel are greater than those given by Jóhannesson’s formula. As expected from the theory of Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others (1989), the response time is longer for glaciers with greater depth, and the equilibrium volume change is proportional to the mean thickness of the glacier.
We have compared generalized glacier response to climate change for two different climate regimes. As expected from the work of Reference Oerlemans and FortuinOerlemans and Fortuin (1992) and Reference Braithwaite and ZhangBraithwaite and Zhang (2000), we find that the static sensitivity is greater for glaciers with a larger mass turnover. We also find that, as expected from the theory of Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others (1989), the response time is shorter for glaciers under an alpine climate than for those under a continental climate (smaller massturnover). As time progresses, for the continental-climate case, the longer response time tends to offset the effect of the smaller static sensitivity. Hence, for the first few centuries the continental-climate glaciers show smaller volume and area changes than the alpine-climate glaciers. After 250 years, however, for the glacier with a widening channel, the volume and area changes of continental-climate glaciers are larger than those of the alpine glaciers. Thus, although for the next century we may expect greater changes in volume from alpine glaciers, the equilibrium or committed change is greater for the continental glaciers.
In our final sensitivity analysis, we show that for the glacier shapes and climate regimes considered, a 1°C increase in temperature gives the same static response as a 35% change in precipitation. However, a smaller change in precipitation is needed to give the same equilibrium response.
Our sensitivity studies have shown that the e-folding time of our coupled model is governed by the same factors as found in the analytic solution of the response time derived for a similar model by Reference Raper, Briffa and WigleyRaper and others (1996). These factors include the glacier depth and the mass-balance at the terminus as shown by Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others (1989). In addition, the e-folding time is dependent on the current geometry of the glacier and how that geometry changes with time. This leads to differences between our e-folding times and Jóhannesson’s volume-response time.
We conclude that the coupled mass-balance geometric model is suitable for the purpose of estimating the contribution to sea-level rise from glaciers and ice caps. Indeed, such a model is essential for sea-level rise estimates for the stabilization scenarios that are now being considered by the IPCC (Reference SchimelSchimel and others, 1997). This is demonstrated by our finding that for a given change in temperature or precipitation, although alpine glaciers are expected to show a rapid response, as has indeed been observed, the commitment in terms of eventual glacier volume change is in fact greater for continental glaciers and ice caps.
Acknowledgements
The work was supported by the Commission of the European Communities Framework IV project “Climate Change and Sea Level” (ENV4-CT095-0124). The authors are grateful for helpful comments from T. Jóhannesson and M. Meier.















