Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-25T12:37:24.865Z Has data issue: false hasContentIssue false
  • English
  • Français

Reasoning on 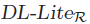with Defeasibility in ASP

Published online by Cambridge University Press:  03 August 2021

LORIS BOZZATO Open the ORCID record for LORIS BOZZATO [Opens in a new window] ,
THOMAS EITER Open the ORCID record for THOMAS EITER [Opens in a new window]  and
LUCIANO SERAFINI Open the ORCID record for LUCIANO SERAFINI [Opens in a new window]
LORIS BOZZATO
Affiliation:
Fondazione Bruno Kessler, Via Sommarive 18, 38123 Trento, Italy (e-mail: bozzato@fbk.eu)
THOMAS EITER
Affiliation:
Technische Universität Wien, Favoritenstraße 9-11, A-1040 Vienna, Austria (e-mail: eiter@kr.tuwien.ac.at)
LUCIANO SERAFINI
Affiliation:
Fondazione Bruno Kessler, Via Sommarive 18, 38123 Trento, Italy (e-mail: serafini@fbk.eu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Reasoning on defeasible knowledge is a topic of interest in the area of description logics, as it is related to the need of representing exceptional instances in knowledge bases. In this direction, in our previous works we presented a framework for representing (contextualized) OWL RL knowledge bases with a notion of justified exceptions on defeasible axioms: reasoning in such framework is realized by a translation into ASP programs. The resulting reasoning process for OWL RL, however, introduces a complex encoding in order to capture reasoning on the negative information needed for reasoning on exceptions. In this paper, we apply the justified exception approach to knowledge bases in 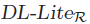, that is, the language underlying OWL QL. We provide a definition for 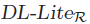knowledge bases with defeasible axioms and study their semantic and computational properties. In particular, we study the effects of exceptions over unnamed individuals. The limited form of 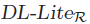axioms allows us to formulate a simpler ASP encoding, where reasoning on negative information is managed by direct rules. The resulting materialization method gives rise to a complete reasoning procedure for instance checking in 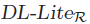with defeasible axioms.1

Keywords

defeasible knowledgedescription logicsanswer set programmingjustifiable exceptions
Type
Original Article
Information
Theory and Practice of Logic Programming , Volume 22 , Issue 2: Special Issue on the International Joint Conference on Rules and Reasoning, RuleML+RR 2019 , March 2022 , pp. 254 - 304
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

We thank the reviewers for their constructive comments and suggestions to improve this paper.

References

Alviano, M. and Faber, W. 2018. Aggregates in answer set programming. Künstliche Intelligence 32, 2–3, 119–124.CrossRefGoogle Scholar
Baader, F., Calvanese, D., McGuinness, D., Nardi, D. and Patel-Schneider, P., Eds. 2003. The Description Logic Handbook. Cambridge University Press.Google Scholar
Bichler, M., Morak, M. and Woltran, S. 2016. The power of non-ground rules in answer set programming. Theory and Practice of Logic Programming 16, 5-6, 552–569.CrossRefGoogle Scholar
Bonatti, P. A., Faella, M., Petrova, I. and Sauro, L. 2015. A new semantics for overriding in description logics. Artificial Intelligence 222, 1–48.CrossRefGoogle Scholar
Bonatti, P. A., Faella, M. and Sauro, L. 2011. Defeasible inclusions in low-complexity DLs. Journal of Artificial Intelligence Research 42, 719–764.Google Scholar
Bonatti, P. A., Lutz, C. and Wolter, F. 2006. Description logics with circumscription. See Doherty et al. (2006), 400–410.Google Scholar
Bozzato, L., Eiter, T. and Serafini, L. 2014. Contextualized knowledge repositories with justifiable exceptions. In 27th International Workshop on Description Logics (DL2014), Bienvenu, M., Ortiz, M., Rosati, R., and Simkus, M., Eds. CEUR Workshop Proceedings, vol. 1193. CEUR-WS.org, 112–123.Google Scholar
Bozzato, L., Eiter, T. and Serafini, L. 2018. Enhancing context knowledge repositories with justifiable exceptions. Artificial Intelligence 257, 72–126.CrossRefGoogle Scholar
Bozzato, L., Eiter, T. and Serafini, L. 2019a. Reasoning on with defeasibility in ASP. In 3rd International Joint Conference on Rules and Reasoning (RuleML+RR 2019), Fodor, P., Montali, M., Calvanese, D., and Roman, D., Eds. Lecture Notes in Computer Science, vol. 11784. Springer, 19–35.Google Scholar
Bozzato, L., Eiter, T. and Serafini, L. 2019b. Reasoning with justifiable exceptions in contextualized knowledge repositories. In Description Logic, Theory Combination, and All That - Essays Dedicated to Franz Baader on the Occasion of His 60th Birthday, Lutz, C., Sattler, U., Tinelli, C., Turhan, A., and Wolter, F., Eds. Lecture Notes in Computer Science, vol. 11560. Springer, 110–134.Google Scholar
Bozzato, L., Homola, M. and Serafini, L. 2012. Towards more effective tableaux reasoning for CKR. In 25th International Workshop on Description Logics (DL2012), Kazakov, Y., Lembo, D., and Wolter, F., Eds. CEUR Workshop Proceedings, vol. 846. CEUR-WS.org, 114–124.Google Scholar
Bozzato, L. and Serafini, L. 2013. Materialization calculus for contexts in the semantic web. In 26th International Workshop on Description Logics (DL2013), Eiter, T., Glimm, B., Kazakov, Y., and Krötzsch, M., Eds. CEUR Workshop Proceedings, vol. 1014. CEUR-WS.org, 552–572.Google Scholar
Bozzato, L., Serafini, L. and Eiter, T. 2018. Reasoning with justifiable exceptions in contextual hierarchies. In 16th International Conference on Principles of Knowledge Representation and Reasoning (KR 2018), Thielscher, M., Toni, F., and Wolter, F., Eds. AAAI Press, 329–338.Google Scholar
Britz, K. and Varzinczak, I. J. 2016. Introducing role defeasibility in description logics. In 15th European Conference on Logics in Artificial Intelligence (JELIA 2016), Michael, L. and Kakas, A. C., Eds. LNCS, vol. 10021. 174–189.Google Scholar
Buccafurri, F., Faber, W. and Leone, N. 1999. Disjunctive logic programs with inheritance. In 16th International Conference on Logic Programming (ICLP 1999), D. D. Schreye, Ed. MIT Press, 79–93.Google Scholar
Cadoli, M. and Lenzerini, M. 1994. The complexity of propositional closed world reasoning and circumscription. Journal of Computer and System Sciences 48, 2, 255–310.CrossRefGoogle Scholar
Cal, A., Gottlob, G. and Lukasiewicz, T. 2012. A general datalog-based framework for tractable query answering over ontologies. J. Web Semant. 14, 57 – 83.CrossRefGoogle Scholar
Calvanese, D., De Giacomo, G., Lembo, D., Lenzerini, M. and Rosati, R. 2007. Tractable reasoning and efficient query answering in description logics: The DL-Lite family. J. Automated Reasoning 39, 3, 385–429.CrossRefGoogle Scholar
Casini, G. and Straccia, U. 2010. Rational closure for defeasible description logics. See Janhunen and Niemelä (2010), 77–90.Google Scholar
Casini, G., Straccia, U. and Meyer, T. 2019. A polynomial time subsumption algorithm for nominal safe under rational closure. Information Science 501, 588–620.CrossRefGoogle Scholar
de Bruijn, J., Eiter, T., Polleres, A. and Tompits, H. 2011. Embedding nonground logic programs into autoepistemic logic for knowledge-base combination. ACM Transactions on Computational Logic 12, 3, 20:1–20:39.CrossRefGoogle Scholar
de Bruijn, J., Eiter, T. and Tompits, H. 2008. Embedding approaches to combining rules and ontologies into autoepistemic logic. In 11th International Conference on Principles of Knowledge Representation and Reasoning (KR 2008), Brewka, G. and Lang, J., Eds. AAAI Press, 485–495.Google Scholar
Doherty, P., Mylopoulos, J. and Welty, C. A., Eds. 2006. 10th International Conference on Principles of Knowledge Representation and Reasoning (KR 2006). AAAI Press.Google Scholar
Eiter, T., Ianni, G., Lukasiewicz, T., Schindlauer, R. and Tompits, H. 2008. Combining answer set programming with description logics for the semantic web. Artif. Intell. 172, 12–13, 1495–1539.CrossRefGoogle Scholar
Eiter, T., Lukasiewicz, T. and Predoiu, L. 2016. Generalized consistent query answering under existential rules. In 15th International Conference on Principles of Knowledge Representation and Reasoning (KR 2016), Baral, C., Delgrande, J. P., and Wolter, F., Eds. AAAI Press, 359–368.Google Scholar
Fitting, M. 1996. First-Order Logic and Automated Theorem Proving, 2nd ed. Graduate Texts in Computer Science. Springer.CrossRefGoogle Scholar
Gelfond, M. and Lifschitz, V. 1991. Classical negation in logic programs and disjunctive databases. New Generation Computing 9, 3/4, 365–386.Google Scholar
Giordano, L., Gliozzi, V., Olivetti, N. and Pozzato, G. L. 2011. Reasoning about Typicality in Low Complexity DLs: The Logics and . In 22nd International Joint Conference on Artificial Intelligence (IJCAI 2011), T. Walsh, Ed. IJCAI/AAAI, 894–899.Google Scholar
Giordano, L., Gliozzi, V., Olivetti, N. and Pozzato, G. L. 2013. A non-monotonic description logic for reasoning about typicality. Artificial Intelligence 195, 165–202.CrossRefGoogle Scholar
Grosof, B. N., Horrocks, I., Volz, R. and Decker, S. 2003. Description logic programs: Combining logic programs with description logic. In 12th International World Wide Web Conference (WWW 2003), Hencsey, G., White, B., Chen, Y. R., Kovács, L., and Lawrence, S., Eds. ACM, 48–57.CrossRefGoogle Scholar
Horrocks, I., Kutz, O., and Sattler, U. 2006. The even more irresistible . See Doherty et al. (2006), 57–67.Google Scholar
Janhunen, T. and Niemelä, I., Eds. 2010. 12th European Conference on Logics in Artificial Intelligence (JELIA 2010) . Lecture Notes in Computer Science, vol. 6341. Springer.Google Scholar
Krötzsch, M. 2010. Efficient inferencing for OWL EL. See Janhunen and Niemelä (2010), 234–246.Google Scholar
Lembo, D., Lenzerini, M., Rosati, R., Ruzzi, M. and Savo, D. F. 2010. Inconsistency-tolerant semantics for description logics. In 4th International Conference on Web Reasoning and Rule Systems (RR 2010), Hitzler, P. and Lukasiewicz, T., Eds. Lecture Notes in Computer Science, vol. 6333. Springer, 103–117.Google Scholar
Lifschitz, V., Pearce, D. and Valverde, A. 2001. Strongly equivalent logic programs. ACM Transactions on Computational Logic 2, 4, 526–541.CrossRefGoogle Scholar
Motik, B., Fokoue, A., Horrocks, I., Wu, Z., Lutz, C. and Grau, B. C. 2009. OWL 2 Web Ontology Language Profiles. W3C recommendation, W3C. October. http://www.w3.org/TR/2009/REC-owl2-profiles-20091027/ Google Scholar
Pensel, M. and Turhan, A. 2017. Including quantification in defeasible reasoning for the description logic . In 14th International Conference on Logic Programming and Nonmonotonic Reasoning (LPNMR 2017), Balduccini, M. and Janhunen, T., Eds. Lecture Notes in Computer Science, vol. 10377. Springer, 78–84.Google Scholar
Pensel, M. and Turhan, A. 2018. Reasoning in the defeasible description logic - computing standard inferences under rational and relevant semantics. International Journal of Approximate Reasoning 103, 28–70.CrossRefGoogle Scholar
Serafini, L. and Homola, M. 2012. Contextualized knowledge repositories for the semantic web. Journal of Web Semantics 12, 64–87.CrossRefGoogle Scholar
Woltran, S. 2008. A common view on strong, uniform, and other notions of equivalence in answer-set programming. Theory and Practice of Logic Programming 8, 2, 217–234.CrossRefGoogle Scholar