Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-09T00:42:18.804Z Has data issue: false hasContentIssue false
  • English
  • Français

An Upper Bound on the Space Complexity of Random Formulae in Resolution

Published online by Cambridge University Press:  15 February 2003

Michele Zito
Michele Zito*
Affiliation:
Department of Computer Science, University of Liverpool, Chadwick Building, Peach Street, Liverpool L69 7ZF, UK; M.Zito@csc.liv.ac.uk.
Get access

Abstract

We prove that, with high probability, the space complexity of refuting a random unsatisfiable Boolean formula in k-CNF on n variables and m = Δn clauses is $O\left(n \cdot \Delta^{-\frac{1}{k-2}}\right)$.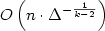

Keywords

Random formulaespace complexitysatisfiability threshold.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 36 , Issue 4 , October 2002 , pp. 329 - 339
Copyright
© EDP Sciences, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

D. Achlioptas and G.B. Sorkin, Optimal myopic algorithms for random 3-SAT, in 41st Annual Symposium on Foundations of Computer Science (2000) 590-600.
M. Alekhnovich, E. Ben-Sasson, A.A. Razborov and A. Wigderson, Space complexity in propositional calculus, in Proc. of the 32nd Annual ACM Symposium on Theory of Computing. Portland, OR (2000).
P. Beame, R. Karp, T. Pitassi and M. Saks, On the complexity of unsatisfiability proofs for random k-CNF formulas, in Proc. of the 30th Annual ACM Symposium on Theory of Computing. New York (1998) 561-571.
E. Ben-Sasson and N. Galesi, Space complexity of random formulae in resolution, in Proc. of the 16th Annual IEEE Conference on Computational Complexity. IEEE Computer Society (2001).
Bollobás, B., Borgs, C., Chayes, J.T., Kim, J.H. and Wilson, D.B., The scaling window of the 2-SAT transition. Random Structures Algorithms 18 (2001) 201-256. CrossRef
P. Cheeseman, B. Kanefsky and W.M. Taylor, Where the really hard problems are, in Proc. of IJCAI-91, edited by Kauffmann (1991) 331-337.
Chvátal, V. and Szemerédi, E., Many hard examples for resolution. J. ACM 35 (1988) 759-768. CrossRef
Cook, S.A. and Reckhow, R., The relative efficiency of propositional proof systems. J. Symb. Logic 44 (1979) 36-50. CrossRef
Davis, M., Logemann, G. and Loveland, D., A machine program for theorem proving. Commun. ACM 5 (1962) 394-397. CrossRef
Davis, M. and Putnam, H., A computing procedure for quantification theory. J. ACM 7 (1960) 201-215. CrossRef
J. Esteban and J.L. Toran, Space bounds for resolution, edited by C. Meinel and S. Tison, in STACS 99: 16th Annual Symposium on Theoretical Aspects of Computer Science, Trier, Germany, March 1999, Proceedings. Springer-Verlag, Lecture Notes in Comput. Sci. 1563 (1999) 551-560.
Goerdt, A., A threshold for unsatisfiability. J. Comput. System Sci. 53 (1996) 469-486. CrossRef
Hagerup, T. and Rüb, C., A guided tour of Chernoff bounds. Inform. Process. Lett. 33 (1989) 305-308. CrossRef
A.C. Kaporis, L.M. Kirousis, Y.C. Stamatiou, M. Vamvakari and M. Zito, Coupon collectors, q-binomial coefficients and the unsatisfiability threshold, edited by A. Restivo, S. Ronchi della Rocca and L. Roversi. Theoret. Comput. Sci., in 7th Italian Conference, ICTCS 2001. Springer-Verlag, Lecture Notes in Comput. Sci. 2202 (2001) 328-338.
R. Bruce King, Beyond the quartic equation. Birkhauser, Boston, MA (1996).
Bruce King, R. and Rodney Canfield, E., An algorithm for calculating the roots of a general quintic equation from its coefficients. J. Math. Phys. 32 (1991) 823-825. CrossRef
I. Stewart, Galois Theory. Chapman and Hall, London (1973).
J. Toran, Lower bounds for the space used in resolution, edited by J. Flum and M. Rodriguez-Artalejo, in Computer Science Logic: 13th International Workshop, CSL'99, 8th Annual Conference of the EACSL, Madrid, Spain, September 20-25, 1999, Proceedings. Springer-Verlag, Lecture Notes in Comput. Sci. 1683 (1999).
B.L. van der Wärden, Algebra. Frederick Ungar Publishing Co., New York (1970).
R.C. Weast, Handbook of Tables for Mathematics. Cleveland: The Chemical Rubber Co. (1964).