Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-18T06:11:06.196Z Has data issue: false hasContentIssue false
  • English
  • Français

XI.—The Zeta Function of Jacobi. A seven-decimal table of Z(u/m) at interval 0·01 for u and for values of m(= k2) from 0·1 to 1·0

Published online by Cambridge University Press:  15 September 2014

L. M. Milne-Thomson
Get access

Extract

The elliptic integral of the second kind

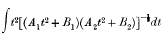
can, by substitution, be made to depend upon

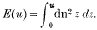
Writing E(K) = E, Jacobi's Zeta function is defined by

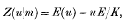
where

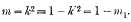
Z(u) is an odd function of u with period 2K.

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 52 , 1933 , pp. 236 - 250
Copyright
Copyright © Royal Society of Edinburgh 1933

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 236 note * Whittaker, and Watson, , Modern Analysis, 22·73.Google Scholar

page 236 note † Milne-Thomson, L. M., Proc. London Math. Soc., (2) 33 (1931).Google Scholar

page 236 note ‡ For five-figure tables of sn u, cn u, dn u, see Milne-Thomson, , Die elliptischen Funktionen von Jacobi, Berlin, Julius Springer, 1931.CrossRefGoogle Scholar

page 236 note § Whittaker and Robinson, Calciava of Observations, ch. vii.

page 237 note * Milne-Thomson, L. M., Journal London Math. Soc., 5 (1930), p. 148.CrossRefGoogle Scholar