Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-21T17:23:34.793Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic solutions for: ẋ(t) = λf(x(t),x(t – 1))

Published online by Cambridge University Press:  14 November 2011

O. Arino  and
R. Benkhalti
O. Arino
Affiliation:
Department of Mathematics, University of Pau, 64000 Pau, France; and Department of Mathematics, College of Liberal Arts, University, MS 38677, U.S.A
R. Benkhalti
Affiliation:
Department of Mathematics & Computer Science, Pacific Lutheran University, Tacoma, WA 98447, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

We present a new result on the existence of periodic solutions for the equation:

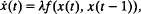
for all positive parameters λ sufficiently large. Our fundamental assumption is the following monotonicity property: if ø ≧ ψ (ø and ψ are data) then x(ø) ≧ x(ψ). The proof consists in applying the global Hopf bifurcation theorem. The main steps are: (i) a classical estimation of the periods; (ii) an a priori estimate for the solutions along a connected branch; (iii) a transformation acting on periodic solutions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 109 , Issue 3-4 , 1988 , pp. 245 - 260
Copyright
Copyright © Royal Society of Edinburgh 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Arino, O.. Contribution à l'étude des comportements des solutions d'équations differentielles à retard par des mérhodes de monotonie et de bifurcation (Thése d'état, chap 5, 1980).Google Scholar
2Arino, O. and Seguier, P.. Existence of oscillating solutions for certain differential equations with delay. Lecture Notes in Mathematics 730 (1979), 46–64.CrossRefGoogle Scholar
3Benkhalti, R.. Méthodes théoriques et numériques dans la détermination de phénomènes de ifurcation globale. (Doctorat de l'Université, Pau, 1986).Google Scholar
4Cooke, K. L.. A course on functional differential equations (Cortona: C.I.M.E., 1979).Google Scholar
5Chow, S. N. and Hale, J.. Methods of bifurcation theory (New York: Springer, 1982).CrossRefGoogle Scholar
6Chow, S. N. and Mallet-Paret, J.. The Fuller index and global Hopf bifurcation. J. Differential Equations 29 (1978), 66–85.CrossRefGoogle Scholar
7Hale, J.. Theory of functional differential equations (New York: Springer, 1977).CrossRefGoogle Scholar
8Hale, J.. Asymptotic behavior of the solutions of differential equations. Proceedings of the symposium on nonlinear oscillations (Kiev: IUTAM, 1961).Google Scholar
9Nussbaum, R. D.. A Hopf global bifurcation theorem for retarded functional differential equations. Trans. Amer. Math. Soc. 238 (1978), 139–164.CrossRefGoogle Scholar