Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T13:14:21.813Z Has data issue: false hasContentIssue false
  • English
  • Français

22.—A Critical Class of Examples concerning the Integrable-square Classification of Ordinary Differential Equations*

Published online by Cambridge University Press:  14 February 2012

W. N. Everitt  and
M. Giertz
W. N. Everitt
Affiliation:
Department of Mathematics, University of Dundee
M. Giertz
Affiliation:
Department of Mathematics, The Royal Institute of Technology, Stockholm, Sweden
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let the coefficient q be real-valued on the half-line [0, ∞) and let q′ be locally absolutely continuous on [0, ∞). The ordinary symmetric differential expressions M and M2 are determined by

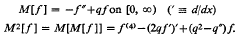
It has been shown in a previous paper by the authors that if for non-negative numbers k and X the coefficient q satisfies the condition

then M is limit-point and M2 is limit–2 at ∞.

This paper is concerned with showing that for powers of the independent variable x the condition (*) is best possible in order that both M and M2 should have the classification at ∞ given above.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 74 , 1976 , pp. 285 - 297
Copyright
Copyright © Royal Society of Edinburgh 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Chaudhuri, Jyoti and Everitt, W. N.. On the square of a formally self-adjoint differential expression. J. Lond. Math. Soc. 1 (1969), 661–673.CrossRefGoogle Scholar
2Everitt, W. N. and Giertz, M.. On the integrable-square classification of ordinary symmetric differential expressions. J. Lond. Math. Soc. 10 (1975), 417–426.CrossRefGoogle Scholar
3Everitt, W. N. and Giertz, M.. On the limit-3 classification of the square of a second-order, linear differential expression. Tritia Mat. 1974–19 (Stockholm: Roy. Inst. Tech.) Also to appear in Czech. Math. J.Google Scholar
4Everitt, W. N. and Giertz, M.. On the deficiency indices of powers of formally symmetric differential expressions. (In Spectral Theory and Differential Equations) Lecture notes in mathematics 448 (Berlin: Springer, 1975).Google Scholar
5Naimark, M. A.. Linear differential operators, Part II (New York: Ungar, 1968).Google Scholar