Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-18T04:24:25.397Z Has data issue: false hasContentIssue false
  • English
  • Français

On functions of bounded boundary rotation I

Published online by Cambridge University Press:  20 January 2009

D. A. Brannan
D. A. Brannan
Affiliation:
Department of Mathematics, Syracuse University, Syracuse, N.Y., 13210
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Vk denote the class of functions

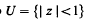which map conformally onto an image domain ƒ(U) of boundary rotation at most kπ (see (7) for the definition and basic properties of the class kπ). In this note we discuss the valency of functions in Vk, and also their Maclaurin coefficients.

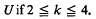In (8) it was shown that functions in Vk are close-to-convex in . Here we show that Vk is a subclass of the class K(α) of close-to-convex functions of order α (10) for 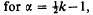, and we give an upper bound for the valency of functions in Vk for K>4.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 16 , Issue 4 , December 1969 , pp. 339 - 347
Copyright
Copyright © Edinburgh Mathematical Society 1969

References

REFERENCES

(1) Brannan, D. A. and Kirwan, W. E.On some classes of bounded univalent functions, J. London Math. Soc. (2) 1 (1969), 431–443.CrossRefGoogle Scholar
(2) Hayman, W. K.Multivalent functions (Cambridge University Press, 1958).Google Scholar
(3) Kirwan, W. E.A note on the coeflScients of functions with bounded boundary rotation, Michigan Math. J. 15 (1968), 277–282.CrossRefGoogle Scholar
(4) Littlewood, J. E.Lectures on the Theory of Functions (Oxford University Press, 1944).Google Scholar
(5) Marx, A.Untersuchungen über schlichte Abbildungen, Math. Ann. 107 (1932), 40–67.CrossRefGoogle Scholar
(6) Macrobert, T. M.Functions of a Complex Variable (MacMillan, London 1958).Google Scholar
(7) Paatero, V.Uber die konforme Abbildungen von Gebieten deren Rander von beschrankter Drehung sind, Ann. Acad. Sci. Fenn. Ser. A, 33 no. 9 (1931).Google Scholar
(8) Pinchuk, B. A variational method for functions of bounded boundary rotation, to appear.Google Scholar
(9) Pommerenke, CH.On the coefficients of close-to-convex functionsy, Michigan Math. J. 9 (1962), 259–269.CrossRefGoogle Scholar
(10) Pommerenke, CH.On starlike and convex functions, J. London Math. Soc. 37 (1962), 209–224.CrossRefGoogle Scholar
(11) Prtvalov, I.I.Randeigenschaften analytischer Funktionen (V. E. B. Deutscher Verlag der Wissenschaften, Berlin 1956).Google Scholar