Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T02:28:51.853Z Has data issue: false hasContentIssue false
  • English
  • Français

More localized automorphisms of the Cuntz algebras

Part of: Selfadjoint operator algebras Topological dynamics

Published online by Cambridge University Press:  05 August 2010

Roberto Conti ,
Jason Kimberley  and
Wojciech Szymański
Roberto Conti
Affiliation:
Mathematics Department, School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia (roberto.conti@newcastle.edu.au; jason.kimberley@newcastle.edu.au)
Jason Kimberley
Affiliation:
Mathematics Department, School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia (roberto.conti@newcastle.edu.au; jason.kimberley@newcastle.edu.au)
Wojciech Szymański
Affiliation:
Mathematics Department, School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia (roberto.conti@newcastle.edu.au; jason.kimberley@newcastle.edu.au) Department of Mathematics and Computer Science, The University of Southern Denmark, Campusvej 55, 5230 Odense M, Denmark (szymanski@imada.sdu.dk)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We completely determine the localized automorphisms of the Cuntz algebras 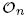corresponding to permutation matrices in Mn ⊗ Mn for n = 3 and n = 4. This result is obtained through a combination of general combinatorial techniques and large scale computer calculations. Our analysis proceeds according to the general scheme proposed in a previous paper, where we analysed in detail the case of 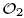using labelled rooted trees. We also discuss those proper endomorphisms of these Cuntz algebras which restrict to automorphisms of their respective diagonals. In the case of 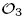we compute the number of automorphisms of the diagonal induced by permutation matrices in M3 ⊗ M3 ⊗ M3.

Keywords

Cuntz algebraendomorphismautomorphismpermutationtree

MSC classification

Secondary: 46L40: Automorphisms 46L05: General theory of $C^*$-algebras 37B10: Symbolic dynamics
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 53 , Issue 3 , October 2010 , pp. 619 - 631
Copyright
Copyright © Edinburgh Mathematical Society 2010

References

1. Araki, H., L. Carey, A. and Evans, D. E., On On+1, J. Operat. Theory 12 (1984), 247–264.Google Scholar
2. J. Archbold, R., On the ‘flip-flop’ automorphism of C*(S1, S2), Q. J. Math. (2) 30 (1979), 129–132.CrossRefGoogle Scholar
3. Bosma, W., Cannon, J., and Playoust, C., The Magma algebra system, I, The user language, J. Symb. Computat. 24 (1997), 235–265.CrossRefGoogle Scholar
4. Conti, R., Kimberley, J. and Szymański, W., Appendix to ‘More localized automorphisms of the Cuntz algebras’, Proc. Edinb. Math. Soc.(2010), DOI:10.1017/ S0013091508010882 (online only).Google Scholar
5. Conti, R. and Pinzari, C., Remarks on the index of endomorphisms of Cuntz algebras, J. Funct. Analysis 142 (1996), 369–405.Google Scholar
6. Conti, R. and Szymański, W., Computing the Jones index of quadratic permutations of endomorphisms of O2, J. Math. Phys. 50 (2009), 012705.Google Scholar
7. Conti, R. and Szymański, W., Labeled trees and localized automorphisms of the Cuntz algebras, Trans. Amer. Math. Soc., in press.Google Scholar
8. Cuntz, J., Simple C*-algebras generated by isometries, Commun. Math. Phys. 57 (1977), 173–185.Google Scholar
9. Cuntz, J., Automorphisms of certain simple C*-algebras, in Quantum fields: algebras, processes(ed. L. Streit), pp. 187–196 (Springer, 1980).Google Scholar
10. Enomoto, M., Fujii, M., Takehana, H. and Watatani, Y., Automorphisms on Cuntz algebras, II, Math. Japon. 24 (1979), 463–468.Google Scholar
11. Enomoto, M., Takehana, H. and Watatani, Y., Automorphisms on Cuntz algebras, Math. Japon. 24 (1979), 231–234.Google Scholar
12. E. Evans, D., On On, Publ. RIMS Kyoto 16 (1980), 915–927.Google Scholar
13. Kawamura, K., Polynomial endomorphisms of the Cuntz algebras arising from permutations, I, General theory, Lett. Math. Phys. 71 (2005), 149–158.CrossRefGoogle Scholar
14. Matsumoto, K. and Tomiyama, J., Outer automorphisms of Cuntz algebras, Bull. Lond. Math. Soc. 25 (1993), 64–66.Google Scholar
15. C. Power, S., Homology for operator algebras, III, Partial isometry homotopy and triangular algebras, New York J. Math. 4 (1998), 35–56.Google Scholar
16. Szymański, W., On localized automorphisms of the Cuntz algebras which preserve the diagonal subalgebra, Proc. RIMS Kyoto 1587 (2008), 109–115.Google Scholar
17. Tsui, S.-K., Some weakly inner automorphisms of the Cuntz algebras, Proc. Am. Math. Soc. 123 (1995), 1719–1725.Google Scholar
Supplementary material: PDF

Conti Appendix

Conti Appendix

Download Conti Appendix(PDF)
PDF 86.9 KB