Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-19T12:04:08.201Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on weighted Bergman spaces and the Cesaro Operator

Published online by Cambridge University Press:  22 January 2016

George Benke  and
Der-Chen Chang
George Benke
Affiliation:
Department of Mathematics, Georgetown University, Washington D.C., 20057, U.S.A., benke@math.georgetown.edu
Der-Chen Chang
Affiliation:
Department of Mathematics Georgetown University, Washington D.C. 20057, U.S.A.chang@math.georgetown.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

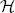Let B denote the unit ball in ℂn, and dV(z) normalized Lebesgue measure on B. For α > -1, define dVα(z) = (1 - \z\2)αdV(z). Let (B) denote the space of holomorhic functions on B, and for 0 < p < ∞, let 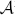p(dVα) denote Lp(dVα) ∩ 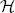(B). In this note we characterize 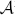p(dVα) as those functions in 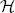(B) whose images under the action of a certain set of differential operators lie in Lp(dVα). This is valid for 1 < p < oo. We also show that the Cesàro operator is bounded on 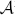p(dVα) for 0 < p < oo. Analogous results are given for the polydisc.

Keywords

32A2532A3665B10
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 159 , 2000 , pp. 25 - 43
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2000

References

[BL] Bell, S. and Ligocka, E., A simplification and extension of Fefferman’s theorem on biholomorphic mappings, Invent. Math., 57 (1980), 283–289.CrossRefGoogle Scholar
[BG] Bonami, A. and Grellier, S., Weighted Bergman projections in domains of finite type in C 2 , Contemporary Math., 189 (1995), 65–80.Google Scholar
[BCG] Bonami, A., Chang, D.C. and Grellier, S., Commutation Properties and Lipschitz estimates for the Bergman and Szegö projections, Math. Zeit., 223 (1996), 275–302.Google Scholar
[Ca] Catlin, D., Subelliptic estimates for the -Neumann problem on pseudoconvex domains, Ann. of Math., 126 (1987), 131–191.Google Scholar
[CL] Chang, D.C. and Li, B.Q., Sobolev and Lipschitz Estimates for weighted Bergman projections, Nagoya Mathematical Journal, 147 (1997), 147–178.Google Scholar
[CNS] Chang, D.C., Nagel, A. and Stein, E.M., Estimates for the -Neumann problem in pseudoconvex domains of finite type in C2 , Acta Mathemtica, 169 (1992), 153–228.CrossRefGoogle Scholar
[D] Duren, P.L., Theory of Hp Spaces, Academic Press, New York, 1970.Google Scholar
[DS] Djrbashian, A.E. and Shamoian, F.A., Topics in the Theory of Ap α Spaces, Teubner Verlagsgellschaft, Leibzig, 1988.Google Scholar
[F] Fefferman, C.L., The Bergman kernel and biholomorphic mappings of pseudoconvex domains, Invent. Math., 26 (1974), 1–65.Google Scholar
[Fo] Forelli, F., Measures whose Poisson integrals are plurisubharmonic, Illinois J. Math., 18 (1974), 373–388.Google Scholar
[HL] Hardy, G.H. and Littlewoood, J.E., Some properties of fractional integrals II, Math. Zeit., 34 (1932), 403–439.Google Scholar
[K] Krantz, S.G., Function Theory of Several Complex Variables (2nd edition), Wadsworth & Brooks/Cole, Pacific Grove, California, 1992.Google Scholar
[M] Miao, J., The Cesáro operator is bounded on Hp for 0 < p ≤ 1, Proc. Amer. Math. Soc., 116 (1992), 1077–1079.Google Scholar
[R] Rudin, W., Function Theory on the Unit Ball of n , Springer-Verlag, Berlin·New York·Heidelberg, 1980.CrossRefGoogle Scholar
[Si] Siskakis, A.G., The Cesáro operator is bounded on H1 , Proc. Amer. Math. Soc., 110 (1990), 461–462.Google Scholar
[T] Titchmarsh, E.C., The Theory of Functions, Oxford University Press, London, 1968.Google Scholar
[Z] Zhu, K., Operator Theory in Function Spaces, Marcel Dekker, Inc., New York· Basel, 1990.Google Scholar