Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-18T15:13:35.362Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SIMPLE ZEROS OF THE DEDEKIND ZETA-FUNCTION OF A QUADRATIC NUMBER FIELD

Part of: Zeta and $L$-functions: analytic theory Algebraic number theory: global fields

Published online by Cambridge University Press:  22 May 2019

Xiaosheng Wu  and
Lilu Zhao
Xiaosheng Wu
Affiliation:
School of Mathematics, Hefei University of Technology, Hefei 230009, China email xswu@amss.ac.cn
Lilu Zhao
Affiliation:
School of Mathematics, Shandong University, Jinan 250100, China email zhaolilu@sdu.edu.cn
Get access

Abstract

We study the number of non-trivial simple zeros of the Dedekind zeta-function of a quadratic number field in the rectangle 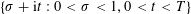$\{\unicode[STIX]{x1D70E}+\text{i}t:0<\unicode[STIX]{x1D70E}<1,0<t<T\}$. We prove that such a number exceeds 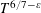$T^{6/7-\unicode[STIX]{x1D700}}$ if 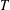$T$ is sufficiently large. This improves upon the classical lower bound 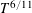$T^{6/11}$ established by Conrey et al [Simple zeros of the zeta function of a quadratic number field. I. Invent. Math.86 (1986), 563–576].

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$ 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses 11R42: Zeta functions and $L$-functions of number fields
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 851 - 861
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bombieri, E. and Iwaniec, H., On the order of 𝜁(1/2 + it). Ann. Sc. Norm. Super. Pisa Cl. Sci 4(13) 1986, 449–472.Google Scholar
Bourgain, J., Decoupling, exponential sums and the Riemann zeta function. J. Amer. Math. Soc. 30 2017, 205–224.10.1090/jams/860Google Scholar
Bui, H., Conrey, J. B. and Young, M., More than 41% of the zeros of the zeta function are on the critical line. Acta Arith. 150(1) 2011, 35–64.10.4064/aa150-1-3Google Scholar
Bui, H. and Heath-Brown, D. R., On simple zeros of the Riemann zeta-function. Bull. Lond. Math. Soc. 45 2013, 953–961.10.1112/blms/bdt026Google Scholar
Conrey, J. B., More than two fifths of the zeros of the Riemann zeta function are on the critical line. J. Reine Angew. Math. 339 1989, 1–26.Google Scholar
Cheer, A. Y. and Goldston, D. A., Simple zeros of the Riemann zeta-function. Proc. Amer. Math. Soc. 118 1993, 365–373.10.1090/S0002-9939-1993-1132849-0Google Scholar
Conrey, J. B., Ghsoh, A. and Gonek, S. M., Simple zeros of the zeta function of a quadratic number field. I. Invent. Math. 86 1986, 563–576.10.1007/BF01389269Google Scholar
Conrey, J. B., Ghsoh, A. and Gonek, S. M., Simple zeros of the zeta function of a quadratic number field. II. In Analytic Number Theory and Diophantine Problems (Stillwater, OK, 1984) (Progress in Mathematics 70 ), Birkhäuser (Boston, MA, 1987), 87–114.10.1007/978-1-4612-4816-3_5Google Scholar
Conrey, J. B., Ghsoh, A. and Gonek, S. M., Simple zeros of the Riemann zeta-function. Proc. Lond. Math. Soc. 76 1998, 497–522.10.1112/S0024611598000306Google Scholar
Feng, S., Zeros of the Riemann zeta function on the critical line. J. Number Theory 132(4) 2012, 511–542.10.1016/j.jnt.2011.10.002Google Scholar
Heath-Brown, D. R., Simple zeros of the Riemann zeta-function on the critical line. Bull. Lond. Math. Soc. 11 1979, 17–18.10.1112/blms/11.1.17Google Scholar
Ivić, A., The Riemann Zeta-function: Theory and Applications, Wiley (New York, 1985) ; reprinted by Dover Publications in 2013.Google Scholar
Levinson, N., More than one third of zeros of Riemann’s zeta-function are on 𝜎 = 1/2. Adv. Math. 13 1974, 383–436.10.1016/0001-8708(74)90074-7Google Scholar
Montgomery, H. L., Topics in Multiplicative Number Theory (Lecture Notes in Mathematics 227 ), Springer (Berlin–Heidelberg–New York, 1971).10.1007/BFb0060851Google Scholar
Montgomery, H. L., Distribution of the zeros of the Riemann zeta function. Proc. Int. Congr. Math 1 1974, 379–381.Google Scholar
Pratt, K., Robles, N., Zaharescu, A. and Zeindler, D., Combinatorial applications of autocorrelation ratios. Preprint, 2018, arXiv:1802.10521.Google Scholar
Selberg, A., On the zeros of Riemann’s zeta-function. Skr. Nor. Vidensk.-Akad. Oslo, I 10 1942, 1–59.Google Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-function, revised by D. R. HeathBrown, 2nd edn., Clarendon Press (Oxford, 1986).Google Scholar
Wu, X., The twisted mean square and critical zeros of Dirichlet $L$ -functions. Math. Z. (2018), doi:10.1007/s00209-018-2209-8.Google Scholar