Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-15T10:15:14.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Portraits of preperiodic points for rational maps

Published online by Cambridge University Press:  08 May 2015

DRAGOS GHIOCA ,
KHOA NGUYEN  and
THOMAS J. TUCKER
DRAGOS GHIOCA
Affiliation:
Department of Mathematics University of British Columbia Vancouver, BC V6T 1Z2, Canada. e-mail: dghioca@math.ubc.edu
KHOA NGUYEN
Affiliation:
Department of Mathematics University of British Columbia Vancouver, BC V6T 1Z2, Canada. e-mail: dknguyen@math.ubc.ca
THOMAS J. TUCKER
Affiliation:
Department of Mathematics University of Rochester Rochester, NY 14627, USA. e-mail: thomas.tucker@rochester.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be a function field over an algebraically closed field k of characteristic 0, let ϕ ∈ K(z) be a rational function of degree at least equal to 2 for which there is no point at which ϕ is totally ramified and let α ∈ K. We show that for all but finitely many pairs (m, n) ∈ 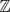$\mathbb{Z}$⩾0 × 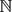$\mathbb{N}$ there exists a place 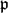$\mathfrak{p}$ of K such that the point α has preperiod m and minimum period n under the action of ϕ. This answers a conjecture made by Ingram–Silverman [13] and Faber–Granville [8]. We prove a similar result, under suitable modification, also when ϕ has points where it is totally ramified. We give several applications of our result, such as showing that for any tuple (c0, . . ., cd−2) ∈ kd−1 and for almost all pairs (mi, ni) ∈ 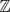$\mathbb{Z}$⩾0 × 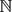$\mathbb{N}$ for i = 0, . . ., d − 2, there exists a polynomial f ∈ k[z] of degree d in normal form such that for each i = 0, . . ., d − 2, the point ci has preperiod mi and minimum period ni under the action of f.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 159 , Issue 1 , July 2015 , pp. 165 - 186
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baker, M. A finiteness theorem for canonical heights associated to rational maps over function fields. J. Reine Angew. Math. 626 (2009) 205–233 Google Scholar
[2] Bang, A. S. Taltheoretiske Undersogelse. Tidsshrift Mat. 4 (1886), 70–80, 130–137.Google Scholar
[3] Benedetto, R. L. Heights and preperiodic points for polynomials over function fields. 62 (2005) 3855–3866 Google Scholar
[4] Bombieri, E. and Gubler, W. Heights in Diophantine geometry. New Math. Mono. Cambridge Univ. Press, Cambridge (2006).Google Scholar
[5] Call, G. S. and Silverman, J. H. Canonical heights on varieties with morphisms. Compositio Math. 89 (1993) 163–205 Google Scholar
[6] Douady, A. and Hubbard, J. A proof of Thurston's topological characterization of rational functions. Acta Math. 171 (1993), 263–297.Google Scholar
[7] Doyle, J. Preperiodic portraits for unicritical polynomials. Submitted for publication, http://arxiv.org/pdf/1501.06821 Google Scholar
[8] Faber, X. and Granville, A. Prime factors of dynamical sequences J. Reine Angew. Math. 661 (2011) 189–214 Google Scholar
[9] Ghioca, D. and Hsia, L.-C. Torsion points in families of Drinfeld modules. Acta Arith. 161 (2013) 219–240 Google Scholar
[10] Ghioca, D. and Tucker, T. J. Equidistribution and integral points for Drinfeld modules. Trans. Amer. Math. Soc. 360 (2008) 4863–4887 Google Scholar
[11] Gratton, C., Nguyen, K. and Tucker, T. J. ABC implies primitive prime divisors in arithmetic dynamics. Bull. London Math. Soc. 45 (2013) 1194–1208 Google Scholar
[12] Hsia, L.-C. On the reduction of a non-torsion point of a Drinfeld module. J. Number Theory 128 (2008) 1458–1484 Google Scholar
[13] Ingram, P. and Silverman, J. H. Primitive divisors in arithmetic dynamics. Math. Proc. Camb. Phil. Soc. 146 (2009) 289–302 Google Scholar
[14] Khadjavi, L. S. An effective version of Belyi's theorem. J. Number Theory. 96 (2002), no. 1, 22–47.Google Scholar
[15] Kisaka, M. On some exceptional rational maps. Proc. Japana Acad. 71, Ser. A (1995), 35–38.Google Scholar
[16] Krieger, H. Primitive prime divisors in the critical orbit of zd + c. to appear in Int. Math. Res. Not. Google Scholar
[17] Mason, R. C. Diophantine equations over function fields. London Math. Soc. Lecture Note Ser., vol. 96 (Cambridge University Press, Cambridge, (1984).Google Scholar
[18] Schinzel, A. Primitive divisors of the expression an–bn in algebraic number fields. J. Reine Angew. Math. 268/269 (1974), 27–33.Google Scholar
[19] Silverman, J. The S-unit equation over function fields. Math. Proc. Camb. Phil. Soc. 95 (1984) (1) 3–4 Google Scholar
[20] Silverman, J. H. The arithmetic of dynamical systems. Graduate Texts in Math. 241 (Springer, New York, (2007), x+511 pp.Google Scholar
[21] Stothers, W. W. Polynomial identities and Hauptmoduln. Quart. J. Math. Oxford Ser. (2) 32 (1981) (127) 349–370 Google Scholar
[22] Yamanoi, K. The second main theorem for small functions and related problems. Acta Math. 192 (2004) (2) 225–294 Google Scholar
[23] Vojta, P. A more general abc conjecture. Int. Math. Res. Not. 21 (1998) 1103–1116 Google Scholar
[24] Vojta, P. Diophantine approximations and value distribution theory. Lecture Notes in Math. vol. 1239 (Springer–Verlag Berlin, (1987).Google Scholar
[25] Zsigmondy, K. Zur theorie der Potenzreste. Monatsh. Math. Phys. 3 (1892), 265–284.Google Scholar