Hostname: page-component-5cf477f64f-xc2pj Total loading time: 0 Render date: 2025-04-01T19:22:32.531Z Has data issue: false hasContentIssue false
  • English
  • Français

The non-equivalence between the trigonometric system and the system of functions with pointwise restrictions on values in the uniform and L1 norms

Published online by Cambridge University Press:  15 March 2011

MICHAŁ WOJCIECHOWSKI
MICHAŁ WOJCIECHOWSKI*
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, Sniadeckich 8, I p., 00-956 Warszawa, Poland. e-mail: miwoj-impan@o2.pl
Get access Rights & Permissions [Opens in a new window]

Extract

Let 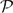n denote the space of trigonometric polynomials of degree n i.e. 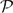n = span(e−ikt : |k| ≤ n) ⊂ Lp(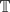) and let (Ω, dx) be any mesurable space with finite measure. In this paper we use the quantitative version of the Helson-Rudin-Cohen idempotent theorem due to Green and Sanders (cf. [3]) to prove the following.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 150 , Issue 3 , May 2011 , pp. 561 - 571
Copyright
Copyright © Cambridge Philosophical Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abramovich, Y. A. and Aliprantis, C. D. Positive operators, in: Handbook of the Geometry of Banach Spaces, edited by Johnson, W. B. and Lindenstrauss, J. (Elsevier 2001), 85–122.CrossRefGoogle Scholar
[2]Dechamps, M. Sous-espaces invariants de L p(G), G groupe ablien compact, Harmonic analysis, Exp. No. 3. Publ. Math. Orsay 81, 8, Univ. Paris XI, Orsay, (1981).Google Scholar
[3]Green, B. and Sanders, T.A quantitative version of the idempotent theorem in harmonic analysis. Ann. of Math. 168 (2008), 1025–1054.CrossRefGoogle Scholar
[4]Helson, H.Note of harmonic functions. Proc. Amer. Math. Soc. 4 (1953), 686–691.CrossRefGoogle Scholar
[5]Helson, H.On a theorem of Szegö. Proc. Amer. Math. Soc. 6 (1955), 235–242.Google Scholar
[6]Konyagin, S.V.On a problem of Littlewood. Math. USSR Izv. 18 2 (1982), 205–225; Izv. Akad. Nauk SSSR 45 (1981), 243–265.CrossRefGoogle Scholar
[7]McGehee, O.C., Pigno, L. and Smith, B.Hardy's inequality and the norm for exponential sums. Ann. of Math. 113 (1981), 613–618.CrossRefGoogle Scholar
[8]Meyer, Y.Endomorphismes des idéaux fermés de L 1(G), classes de Hardy et séries de Fourier lacunaires Ann. Sci. École Norm. 1 (4) (1968).Google Scholar
[9]Pelczynski, A. Selected problems on the structre of complemented subspaces of Banach spaces, in: Methods in Banach Spaces, edited by Castillo, Jesus M. F. and Johnson, William B., London Mathematical Society Lecture Note Series 337, Cambridge University Press (2006), 341–354.CrossRefGoogle Scholar