Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-17T15:02:21.976Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME PROPERTIES OF ANALYTIC DIFFERENCE VALUED FIELDS

Part of: Model theory Differential and difference algebra Non-Archimedean analysis

Published online by Cambridge University Press:  29 May 2015

Silvain Rideau
Silvain Rideau*
Affiliation:
Département des Mathématiques et Applications, École normale supérieure, 45 rue d’Ulm, 75005 Paris, France (silvain.rideau@ens.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove field quantifier elimination for valued fields endowed with both an analytic structure that is $\unicode[STIX]{x1D70E}$-Henselian and an automorphism that is $\unicode[STIX]{x1D70E}$-Henselian. From this result we can deduce various Ax–Kochen–Eršov type results with respect to completeness and the independence property. The main example we are interested in is the field of Witt vectors on the algebraic closure of 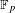$\mathbb{F}_{p}$ endowed with its natural analytic structure and the lifting of the Frobenius. It turns out we can give a (reasonable) axiomatization of its first-order theory and that this theory does not have the independence property.

Keywords

valued fields with an automorphismanalytic structureseparated power series𝜎-HenselianityWitt vectorsNIP

MSC classification

Primary: 03C10: Quantifier elimination, model completeness and related topics 12H10: Difference algebra
Secondary: 03C45: Classification theory, stability and related concepts 32P05: Non-Archimedean analysis (should also be assigned at least one other classification number from Section 32 describing the type of problem) 32B05: Analytic algebras and generalizations, preparation theorems
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 3 , June 2017 , pp. 447 - 499
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aschenbrenner, M., van den Dries, L. and van der Hoeven, J., Toward a model theory for transseries, Notre Dame J. Form. Log. 54(3–4) (2013), 279–310.CrossRefGoogle Scholar
Ax, J. and Kochen, S., Diophantine problems over local fields I, Amer. J. Math. 87(3) (1965), 605–630.CrossRefGoogle Scholar
Azgin (now known as Durhan), S., Valued fields with contractive automorphism and Kaplansky fields, J. Algebra 324(10) (2010), 2757–2785.CrossRefGoogle Scholar
Azgin (now known as Durhan), S. and van den Dries, L., Elementary theory of valued fields with a valuation-preserving automorphism, J. Inst. Math. Jussieu 9(4) (2010), 1–35.Google Scholar
Basarab, S. A., Relative elimination of quantifiers for Henselian valued fields, Ann. Pure Appl. Logic 53(1) (1991), 51–74.CrossRefGoogle Scholar
Basarab, S. A. and Kuhlmann, F.-V., An isomorphism theorem for Henselian algebraic extensions of valued fields, Manuscripta Math. 77 (1992), 113–126.CrossRefGoogle Scholar
Bélair, L., Types dans les corps valués munis d’applications coefficients, Illinois J. Math. 43(2) (1999), 410–424.CrossRefGoogle Scholar
Bélair, L., Macintyre, A. and Scanlon, T., Model theory of the Frobenius on the Witt vectors, Amer. J. Math. 129(3) (2007), 665–721.CrossRefGoogle Scholar
Cluckers, R. and Lipshitz, L., Fields with analytic structure, J. Eur. Math. Soc. (JEMS) 13(4) (2011), 1147–1223.CrossRefGoogle Scholar
Cluckers, R. and Lipshitz, L., Strictly convergent analytic structures, preprint, 2013, arXiv:1312.5932: to appear in J. Eur. Math. Soc. (JEMS).Google Scholar
Cluckers, R., Lipshitz, L. and Robinson, Z., Analytic cell decomposition and analytic motivic integration, Ann. Sci. Éc. Norm. Supér. (4) 39(4) (2006), 535–568.CrossRefGoogle Scholar
Cluckers, R. and Loeser, F., B-minimality, J. Math. Log. 7(02) (2007), 195–227.CrossRefGoogle Scholar
Delon, F., Types sur ℂ((x)), in Groupe d’étude sur les théories stables, année 2, 1978/79, exp. 5, pp. 1–29 (Secrétariat Mathematics, 1981).Google Scholar
Denef, J. and van den Dries, L., p-adic and real subanalytic sets, Ann. of Math. (2) 128 (1988), 79–138.CrossRefGoogle Scholar
van den Dries, L., Analytic Ax–Kochen–Eršov theorems, in Proceedings of the International Conference on Algebra, Contemporary Mathematics, Volume 3, pp. 379–398 (American Mathematical Society, 1992).Google Scholar
van den Dries, L., Haskell, D. and Macpherson, D., One-dimensional p-adic sub analytic sets, J. Lond. Math. Soc. (2) 59(1) (1999), 1–20.CrossRefGoogle Scholar
Durhan, S. and Onay, G., Quantifier elimination for valued fields equipped with an automorphism, preprint, 2013, arXiv:1309.5751.Google Scholar
Gurevich, Y. and Schmitt, P. H., The theory of ordered abelian groups does not have the independence property, Trans. Amer. Math. Soc. 284(1) (1984), 171–182.CrossRefGoogle Scholar
Guzy, N. and Point, F., Topological differential fields, Ann. Pure Appl. Logic 161(4) (2010), 570–598.CrossRefGoogle Scholar
Hrushovski, E., The elementary theory of the Frobenius automorphism, preprint, 2004, arXiv:0406514.Google Scholar
Hrushovski, E. and Kazhdan, D., Integration in valued fields, in Algebraic Geometry and Number Theory, Progress of Mathematics, Volume 253, pp. 261–405 (Birkhäuser Boston, Boston, MA, 2006).CrossRefGoogle Scholar
Kuhlmann, F.-V., Quantifier elimination for henselian fields relative to additive and multiplicative congruences, Israel J. Math. 85 (1994), 277–306.CrossRefGoogle Scholar
Lipshitz, L. and Robinson, Z., Rigid subanalytic subsets of curves and surfaces, J. Lond. Math. Soc. (2) 59(3) (1999), 895–921.CrossRefGoogle Scholar
Lipshitz, L. and Robinson, Z., Rings of separated power series, Astérisque 264 (2000), 3–108.Google Scholar
Lipshitz, L. and Robinson, Z., Uniform properties of rigid subanalytic sets, Trans. Amer. Math. Soc. 357(11) (2005), 4349–4377.CrossRefGoogle Scholar
Macintyre, A., On definable subsets of p-adic fields, J. Symbolic Logic 41(3) (1976), 605–610.CrossRefGoogle Scholar
Pal, K., Multiplicative valued difference fields, J. Symbolic Logic 77(2) (2012), 545–579.CrossRefGoogle Scholar
Pas, J., Uniform p-adic cell decomposition and local zeta functions, J. Reine Angew. Math. 399 (1989), 137–172.Google Scholar
Pas, J., On the angular component map modulo p , J. Symbolic Logic 55(3) (1990), 1125–1129.CrossRefGoogle Scholar
Scanlon, T., Model theory of valued $D$ -fields, PhD thesis, Harvard University (1997).Google Scholar
Scanlon, T., A model complete theory of valued D-fields, J. Symbolic Logic 65(4) (2000), 1758–1784.CrossRefGoogle Scholar
Scanlon, T., Quantifier elimination for the relative Frobenius, in Valuation Theory and Its Applications, Conference proceedings of the International Conference on Valuation Theory (Saskatoon, 1999), Vol. II, Fields Institute Communications, Volume 33, pp. 323–352 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Scanlon, T., Analytic difference rings, in Proceedings of the International Congress of Mathematicians, Madrid, Vol. II, pp. 71–92 (European Mathematical Society, Zürich, 2006).Google Scholar