No CrossRef data available.
Article contents
NULL SETS AND COMBINATORIAL COVERING PROPERTIES
Published online by Cambridge University Press: 15 June 2021
Abstract
A subset of the Cantor cube is null-additive if its algebraic sum with any null set is null. We construct a set of cardinality continuum such that: all continuous images of the set into the Cantor cube are null-additive, it contains a homeomorphic copy of a set that is not null-additive, and it has the property 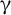 $\unicode{x3b3} $
, a strong combinatorial covering property. We also construct a nontrivial subset of the Cantor cube with the property
$\unicode{x3b3} $
, a strong combinatorial covering property. We also construct a nontrivial subset of the Cantor cube with the property 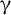 $\unicode{x3b3} $
that is not null additive. Set-theoretic assumptions used in our constructions are far milder than used earlier by Galvin–Miller and Bartoszyński–Recław, to obtain sets with analogous properties. We also consider products of Sierpiński sets in the context of combinatorial covering properties.
$\unicode{x3b3} $
that is not null additive. Set-theoretic assumptions used in our constructions are far milder than used earlier by Galvin–Miller and Bartoszyński–Recław, to obtain sets with analogous properties. We also consider products of Sierpiński sets in the context of combinatorial covering properties.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



