Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-09T03:51:08.848Z Has data issue: false hasContentIssue false
  • English
  • Français

Free set algebras satisfying systems of equations

Published online by Cambridge University Press:  12 March 2014

G. Aldo Antonelli
G. Aldo Antonelli*
Affiliation:
Program in Logic and Philosophy of Science, University of California, Irvine 3151 Social Science Plaza Irvine, CA 92697-5100, USA, E-mail: aldo@uci.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we introduce the notion of a set algebra 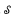satisfying a system E of equations. After defining a notion of freeness for such algebras, we show that, for any system E of equations, set algebras that are free in the class of structures satisfying E exist and are unique up to a bisimulation. Along the way, analogues of classical set-theoretic and algebraic properties are investigated.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 4 , December 1999 , pp. 1656 - 1674
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aczel, P., Non-well-founded sets, Center for the Study of Language and Information, Stanford, CA, 1988.Google Scholar
[2]Antonelli, G.A., Non-well-founded sets via revision rules, Journal of Philosophical Logic, vol. 23 (1994), pp. 633–79, Mathematical Reviews 95k:03086.CrossRefGoogle Scholar
[3]Antonelli, G.A., Extensional quotients for type theory and the consistency problem for NF, this Journal, vol. 63 (1998), no. 1, pp. 247–261.Google Scholar
[4]Barwise, J. and Moss, L., Vicious circles, Center for the Study of Language and Information, Stanford, CA, 1996.Google Scholar
[5]Cohn, P.M., Universal algebra, D. Reidel Publishing Co., Dordrecht and Boston, 1965, 1981.CrossRefGoogle Scholar
[6]Joyal, A. and Moerdijk, I., Algebraic set theory, London Mathematical Society Lecture Note Series, no. 220, Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
[7]Mislove, M., Moss, L., and Oles, F., Non-well-founded sets obtained from ideal fixed points, Information and Computation, vol. 93 (1991), no. 1, pp. 16–54.CrossRefGoogle Scholar
[8]Robinson, D.J.S., A course in the theory of groups, Springer Verlag, Berlin and New York, 1982.CrossRefGoogle Scholar