Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-01T02:13:08.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphism groups of arithmetically saturated models

Published online by Cambridge University Press:  12 March 2014

Ermek S. Nurkhaidarov
Ermek S. Nurkhaidarov*
Affiliation:
Department of Mathematics, University of Montana-Western, Dillon, MT 59725., USA. E-mail: e_nurkh@umwestern.edu
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we study the automorphism groups of countable arithmetically saturated models of Peano Arithmetic. The automorphism groups of such structures form a rich class of permutation groups. When studying the automorphism group of a model, one is interested to what extent a model is recoverable from its automorphism group. Kossak-Schmerl [12] show that if M is a countable, arithmetically saturated model of Peano Arithmetic, then Aut(M) codes SSy(M). Using that result they prove:

Let M1. M2 be countable arithmetically saturated models of Peano Arithmetic such that Aut(M1) ≅ Aut(M2). Then SSy(M1) = SSy(M2).

We show that if M is a countable arithmetically saturated of Peano Arithmetic, then Aut(M) can recognize if some maximal open subgroup is a stabilizer of a nonstandard element, which is smaller than any nonstandard definable element. That fact is used to show the main theorem:

Let M1, M2be countable arithmetically saturated models of Peano Arithmetic such that Aut(M1) ≅ Aut(M2). Then for every n < ω

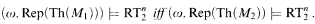
Here RT2n is Infinite Ramsey's Theorem stating that every 2-coloring of [ω]n has an infinite homogeneous set. Theorem 0.2 shows that for models of a false arithmetic the converse of Kossak-Schmerl Theorem 0.1 is not true. Using the results of Reverse Mathematics we obtain the following corollary:

There exist four countable arithmetically saturated models of Peano Arithmetic such that they have the same standard system but their automorphism groups are pairwise non-isomorphic.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 71 , Issue 1 , March 2006 , pp. 203 - 216
Copyright
Copyright © Association for Symbolic Logic 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bamber, N. and Kotlarski, H., On interstices in countably arithmetically saturated models of Peano Arithmeitc, Mathematical Logic Quarterly, vol. 43 (1997), pp. 525–540.CrossRefGoogle Scholar
[2]Barwise, J. and Schlipf, J., On recursively saturated models of arithmetic, Model theory and algebra: a memorial tribute to Abraham Robinson (Saracino, D. H. and Weispfenning, V. B., editors). Lecture notes in mathematics, vol. 498, Springer-Verlag, 1975, pp. 42–55.CrossRefGoogle Scholar
[3]Berline, C., McAloon, K., and Ressayre, J. P., Model theory and arithmetic, Lecture notes in mathematics, vol. 890, Springer-Verlag, 1981.CrossRefGoogle Scholar
[4]Bigorajska, T., Kotlarski, H., and Schmerl, J. H., On regular interstices in countable arithmetically saturated models of Peano Arithmetic, Fundamenta Mathematicae, vol. 158 (1998), pp. 125–146.CrossRefGoogle Scholar
[5]Cholak, P. A., Jockusch, C. G., and Slaman, T. A., On the strength of Ramsey's theorem for pairs, this Journal, vol. 66 (2001), pp. 1–55.Google Scholar
[6]Hirst, J. L., Combinatorics in subsystems of second order arithmetic, Ph.D. thesis, The Pennsylvania State University, 1987.Google Scholar
[7]Kaufmann, M. and Schmerl, J. H., Weak saturation in models of PA, this Journal, vol. 52 (1987), pp. 129–147.Google Scholar
[8]Kaye, R., A Galois correspondence for countable recursively saturated models of Peano's Arithmetic, Automorphisms of first order structures (Kaye, R. and Macpherson, D.. editors), Oxford University Press, 1994, pp. 293–312.CrossRefGoogle Scholar
[9]Kaye, R., Kossak, R., and Kotlarski, H., Automorphisms of recursively saturated models of arithmetic. Annals of Pure and Applied Logic, vol. 55 (1991), pp. 67–91.CrossRefGoogle Scholar
[10]Kirby, L. A., Ultrafilters and types of models of arithmetic, Annals of Pure and Applied Logic, vol. 27 (1984), pp. 215–252.CrossRefGoogle Scholar
[11]Kossak, R., Kotlarski, H., and Schmerl, J. H., On maximal subgroups of the automorphism group of a countable recursively saturated model of PA, Annals of Pure and Applied Logic, vol. 63 (1991), pp. 125–148.Google Scholar
[12]Kossak, R. and Schmerl, J. H., The automorphism group of an arithmetically saturated model of Peano Arithmetic, Journal of the London Mathematical Society, vol. 52 (1995), pp. 235–244.CrossRefGoogle Scholar
[13]Lascar, D., The small index property and recursively saturated models of Peano Arithmetic, Automorphisms of first order structures (Kaye, R. and Macpherson, D., editors), Oxford University Press, 1994, pp. 281–292.CrossRefGoogle Scholar
[14]Schmerl, J. H., Closed normal subgroup, Mathematical Logic Quarterly, vol. 47 (2001), pp. 489–492.3.0.CO;2-8>CrossRefGoogle Scholar
[15]Schmerl, J. H., Moving intersticial gaps, Mathematical Logic Quarterly, vol. 48 (2002), pp. 283–296.3.0.CO;2-#>CrossRefGoogle Scholar
[16]Scott, D., Algebras of sets binumerable in complete extensions of arithmetic, Recursive function theory (Dekker, J. C. E., editor), American Mathematical Society Proceeding of symposia in pure mathematics, vol. V, 1962, pp. 117–122.CrossRefGoogle Scholar
[17]Seetapun, D. and Slaman, T., On the strength of Ramsey's theorem, Notre Dame Journal of Formal Logic, vol. 36 (1995), no. 4, pp. 570–582, Special Issue: Models of arithmetic.CrossRefGoogle Scholar
[18]Simpson, S. G., Subsystems of second order aithmetic, Springer-Verlag, 1998.Google Scholar
[19]Smoryński, C., Back and forth inside a recursively saturated model of arithmetic, Logic colloquium '80 (van Dallen, D., editor), North-Holland, 1982, pp. 273–278.Google Scholar
[20]Wilmers, G. M., Unpublished, 1975, D. Phil. Thesis, Oxford University.Google Scholar