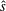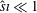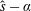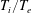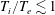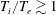1 Introduction
Any magnetic fusion reactor, no matter how carefully designed, is affected by turbulent heat losses, which are detrimental to its performance. The study of turbulent transport processes in magnetically confined plasmas, therefore, has always been of vital importance in the identification of the confinement properties of such devices. A number of plasma quantities are of relevance when evaluating how well the plasma is confined and thus more likely to yield fusion power. Amongst many, there is no doubt that one of the most important is the achievable plasma temperature gradient.
It is known that kinetic plasma instabilities can draw energy from equilibrium plasma gradients and the resulting turbulence cause what is observed as an anomalous energy loss. Perhaps the most important of such instabilities is the ion-temperature-gradient (ITG) driven one, which has been extensively studied both in tokamaks and stellarators. The ITG mode manifests itself in several flavours. Sometimes it is a modified unstable sound wave, as derived for the first time by Rudakov & Sagdeev (Reference Rudakov and Sagdeev1961); it can also arise in the guise of the interchange-type mode of Rosenbluth & Longmire (Reference Rosenbluth and Longmire1956) as a result of equilibrium magnetic field gradients (Horton, Choi & Tang Reference Horton, Choi and Tang1981). It can be of the ballooning type (Connor & Taylor Reference Connor and Taylor1987), with a broad radial structure (Romanelli & Zonca Reference Romanelli and Zonca1993); of the ‘boxing’ type (Plunk et al. Reference Plunk, Helander, Xanthopoulos and Connor2014), or with detailed structure on equilibrium magnetic surfaces (Zocco et al. Reference Zocco, Plunk, Xanthopoulos and Helander2016); of the isolated or general (Dickinson et al. Reference Dickinson, Roach, Skipp and Wilson2014) type, or else ‘passing’ or ‘trapped’ (Dewar Reference Dewar1997); this list may not be complete.
In all these cases, the instability can be categorised in two broad classes which correspond to the slab and the toroidal branch of the mode. In the first case, instability occurs when the equilibrium temperature gradient causes a change in temperature of a perturbation propagating at the sound speed, and such change is in phase with a perturbed
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift, also caused by the presence of the equilibrium temperature gradient (see discussion after (16) of Coppi, Rosenbluth & Sagdeev (Reference Coppi, Rosenbluth and Sagdeev1967)). In toroidal geometry, the coupling of the
$\boldsymbol{E}\times \boldsymbol{B}$
drift, also caused by the presence of the equilibrium temperature gradient (see discussion after (16) of Coppi, Rosenbluth & Sagdeev (Reference Coppi, Rosenbluth and Sagdeev1967)). In toroidal geometry, the coupling of the
![]() $\unicode[STIX]{x1D735}B-$
and curvature drifts with the equilibrium temperature gradient can also destabilise the mode (Horton et al.
Reference Horton, Choi and Tang1981). The intuitive picture of the ITG destabilisation generally holds for very large temperature gradients (fluid limit). However, in many operationally relevant regimes (Mantica et al.
Reference Mantica, Strintzi, Tala, Giroud, Johnson, Leggate, Lerche, Loarer, Peeters and Salmi2009), temperature gradients are not so extreme as to justify a fluid approximation, and it is necessary to account for resonances. The complications associated with such theories escalate very rapidly, and an intuitive picture of the kinetic resonant destabilisation would perhaps be more confusing rather than clarifying. The development of gyrokinetic numerical codes has rescued the situation, and has advanced our understanding of the critical threshold for the destabilisation of the ITG mode.Footnote
1
Inevitably, the interpretation of any linear result produced by a gyrokinetic code is ultimately based on fundamental works, most notably those of Terry, Anderson & Horton (Reference Terry, Anderson and Horton1982), Biglari, Diamond & Rosenbluth (Reference Biglari, Diamond and Rosenbluth1989) and Romanelli (Reference Romanelli1989) (hereafter BDR), for the toroidal branch of the instability, and those of Kadomtsev & Pogutse (Reference Kadomtsev and Pogutse1970), and Hahm & Tang (Reference Hahm and Tang1989) for the finite-shear and shear-less slab branches, respectively.
$\unicode[STIX]{x1D735}B-$
and curvature drifts with the equilibrium temperature gradient can also destabilise the mode (Horton et al.
Reference Horton, Choi and Tang1981). The intuitive picture of the ITG destabilisation generally holds for very large temperature gradients (fluid limit). However, in many operationally relevant regimes (Mantica et al.
Reference Mantica, Strintzi, Tala, Giroud, Johnson, Leggate, Lerche, Loarer, Peeters and Salmi2009), temperature gradients are not so extreme as to justify a fluid approximation, and it is necessary to account for resonances. The complications associated with such theories escalate very rapidly, and an intuitive picture of the kinetic resonant destabilisation would perhaps be more confusing rather than clarifying. The development of gyrokinetic numerical codes has rescued the situation, and has advanced our understanding of the critical threshold for the destabilisation of the ITG mode.Footnote
1
Inevitably, the interpretation of any linear result produced by a gyrokinetic code is ultimately based on fundamental works, most notably those of Terry, Anderson & Horton (Reference Terry, Anderson and Horton1982), Biglari, Diamond & Rosenbluth (Reference Biglari, Diamond and Rosenbluth1989) and Romanelli (Reference Romanelli1989) (hereafter BDR), for the toroidal branch of the instability, and those of Kadomtsev & Pogutse (Reference Kadomtsev and Pogutse1970), and Hahm & Tang (Reference Hahm and Tang1989) for the finite-shear and shear-less slab branches, respectively.
All these analytical theories of the resonant destabilisation of the toroidal ITG were performed in a long-wavelength limit, thus neglecting the full ion Larmor radius response. Here, we present, for the first time, a complete mathematical treatment where this response is retained. The analysis is performed in the local kinetic limit, thus neglecting the variation of the eigenfunction along the magnetic field line, but is valid for arbitrary magnetic geometry. Analytical progress is made by introducing a Padé approximant for the ion response after integrating over the resonances. These are treated by using a new series representation of the Owen
![]() $T$
-function (Owen Reference Owen1956) which exploits the properties of the incomplete Euler gamma function (Tricomi Reference Tricomi1950b
,Reference Tricomi
a
). No approximation for the velocity-space dependence of the particles drifts is made.
$T$
-function (Owen Reference Owen1956) which exploits the properties of the incomplete Euler gamma function (Tricomi Reference Tricomi1950b
,Reference Tricomi
a
). No approximation for the velocity-space dependence of the particles drifts is made.
The threshold for resonant destabilisation of the toroidal branch of the ITG mode is then calculated and compared to previous analytical results and to numerical results obtained from simulations performed with the GENE (Jenko et al.
Reference Jenko, Dorland, Kotschenreuther and Rogers2000) code for a local
![]() ${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak equilibrium (Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1978). In the limit in which the streaming term contribution is negligible)Footnote
2
(
${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak equilibrium (Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1978). In the limit in which the streaming term contribution is negligible)Footnote
2
(
![]() ${\hat{s}}\ll 1$
), we identify a family of unstable ion modes below the threshold for destabilisation of the toroidal branch of the ITG mode. Such modes require high velocity-space resolution to be adequately resolved, they are more unstable for small inverse aspect ratios, and do not show resonant structures for
${\hat{s}}\ll 1$
), we identify a family of unstable ion modes below the threshold for destabilisation of the toroidal branch of the ITG mode. Such modes require high velocity-space resolution to be adequately resolved, they are more unstable for small inverse aspect ratios, and do not show resonant structures for
![]() $v_{\Vert }\neq 0$
. The new critical threshold is studied, for several density gradients, as a function of
$v_{\Vert }\neq 0$
. The new critical threshold is studied, for several density gradients, as a function of
![]() $\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
, where
$\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
, where
![]() $T_{i}$
and
$T_{i}$
and
![]() $T_{e}$
are the ion and electron temperature, respectively. For
$T_{e}$
are the ion and electron temperature, respectively. For
![]() $\unicode[STIX]{x1D70F}\gtrsim 1$
, the threshold shows a dependence on
$\unicode[STIX]{x1D70F}\gtrsim 1$
, the threshold shows a dependence on
![]() $\unicode[STIX]{x1D70F}$
. For
$\unicode[STIX]{x1D70F}$
. For
![]() $\unicode[STIX]{x1D70F}\lesssim 1$
, the threshold in the inverse temperature-gradient scale
$\unicode[STIX]{x1D70F}\lesssim 1$
, the threshold in the inverse temperature-gradient scale
![]() $R/L_{T}$
is proportional to the inverse density gradient scale,
$R/L_{T}$
is proportional to the inverse density gradient scale,
![]() $R/L_{n}$
.
$R/L_{n}$
.
The same qualitative small-
![]() ${\hat{s}}$
behaviour at marginal stability is observed in the stellarator Wendelstein 7-X, even for flat densities. We have verified that the modes are present for configurations with a small trapped-particle population. From the common features shown in the tokamak and stellarator cases, we argue that these modes are of the Floquet type, and can be described in terms of Mathieu functions. Far from marginality, we propose a general eigenvalue equation that is exact and based on Hill’s mathematical study of the motion of the Lunar perigee (Hill Reference Hill1886).
${\hat{s}}$
behaviour at marginal stability is observed in the stellarator Wendelstein 7-X, even for flat densities. We have verified that the modes are present for configurations with a small trapped-particle population. From the common features shown in the tokamak and stellarator cases, we argue that these modes are of the Floquet type, and can be described in terms of Mathieu functions. Far from marginality, we propose a general eigenvalue equation that is exact and based on Hill’s mathematical study of the motion of the Lunar perigee (Hill Reference Hill1886).
The article is organised as follows. In § 2 we present the numerical results from gyrokinetic simulations that demonstrate the qualitative similar behaviour of low-
![]() ${\hat{s}}$
tokamaks and Wendelstein
${\hat{s}}$
tokamaks and Wendelstein
![]() $7-X$
at marginal stability. In § 3 the critical threshold for the low-shear ITG mode is shown for both the
$7-X$
at marginal stability. In § 3 the critical threshold for the low-shear ITG mode is shown for both the
![]() ${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak equilibrium and Wendelstein 7-X. The exact analytical formula for Floquet modes is given (and solved) in § 4. Conclusions are given in § 5. A series of appendices is attached to elucidate some analytical aspects of the resonant destabilisation of the toroidal ITG.
${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak equilibrium and Wendelstein 7-X. The exact analytical formula for Floquet modes is given (and solved) in § 4. Conclusions are given in § 5. A series of appendices is attached to elucidate some analytical aspects of the resonant destabilisation of the toroidal ITG.
2 Instability thresholds
The description of the resonant destabilisation of the toroidal ITG is based on the following eigenvalue equation (Terry et al. Reference Terry, Anderson and Horton1982; Biglari et al. Reference Biglari, Diamond and Rosenbluth1989; Romanelli Reference Romanelli1989)
where
![]() $\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
,
$\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
,
![]() $\unicode[STIX]{x1D714}$
is the mode complex frequency,
$\unicode[STIX]{x1D714}$
is the mode complex frequency,
![]() $\boldsymbol{k}_{\bot }$
is the wave vector perpendicular to the equilibrium magnetic field,
$\boldsymbol{k}_{\bot }$
is the wave vector perpendicular to the equilibrium magnetic field,
![]() $\hat{v}^{2}=(v_{\Vert }^{2}+v_{\bot }^{2})/v_{\text{thi}}^{2}$
, with
$\hat{v}^{2}=(v_{\Vert }^{2}+v_{\bot }^{2})/v_{\text{thi}}^{2}$
, with
![]() $v_{\text{thi}}=\sqrt{2T_{i}/m_{i}}$
the ion thermal speed and
$v_{\text{thi}}=\sqrt{2T_{i}/m_{i}}$
the ion thermal speed and
![]() $m_{i}$
and
$m_{i}$
and
![]() $n_{0}$
are the ion mass and density, respectively. We are effectively considering a local limit, in the sense that the eigenmode structure along the field-following coordinate is neglected, and we restrict our attention to a particular location along the equilibrium magnetic field. This is equivalent to completely neglecting the slab branch discussed in the introduction, and taking
$n_{0}$
are the ion mass and density, respectively. We are effectively considering a local limit, in the sense that the eigenmode structure along the field-following coordinate is neglected, and we restrict our attention to a particular location along the equilibrium magnetic field. This is equivalent to completely neglecting the slab branch discussed in the introduction, and taking
![]() $k_{\Vert }v_{\text{thi}}\ll \unicode[STIX]{x1D714}$
, where
$k_{\Vert }v_{\text{thi}}\ll \unicode[STIX]{x1D714}$
, where
![]() $k_{\Vert }$
is the parallel wavenumber. The equilibrium distribution function is taken to be Maxwellian,
$k_{\Vert }$
is the parallel wavenumber. The equilibrium distribution function is taken to be Maxwellian,
Two characteristic frequencies are present in (2.1)
with
![]() $\unicode[STIX]{x1D714}_{\ast i}=0.5k_{y}\unicode[STIX]{x1D70C}_{i}v_{\text{thi}}/L_{n}$
,
$\unicode[STIX]{x1D714}_{\ast i}=0.5k_{y}\unicode[STIX]{x1D70C}_{i}v_{\text{thi}}/L_{n}$
,
![]() $\unicode[STIX]{x1D702}_{i}=L_{n}/L_{T}$
, and
$\unicode[STIX]{x1D702}_{i}=L_{n}/L_{T}$
, and
where
![]() $\unicode[STIX]{x1D70C}_{i}=v_{\text{thi}}/\unicode[STIX]{x1D6FA}_{ci}$
is the ion Larmor radius,
$\unicode[STIX]{x1D70C}_{i}=v_{\text{thi}}/\unicode[STIX]{x1D6FA}_{ci}$
is the ion Larmor radius,
![]() $\unicode[STIX]{x1D6FA}_{ci}=eB/(m_{i}c)$
the ion cyclotron frequency,
$\unicode[STIX]{x1D6FA}_{ci}=eB/(m_{i}c)$
the ion cyclotron frequency,
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}=0.5k_{y}\unicode[STIX]{x1D70C}_{i}v_{\text{thi}}/a$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}=0.5k_{y}\unicode[STIX]{x1D70C}_{i}v_{\text{thi}}/a$
and
![]() $\unicode[STIX]{x1D714}_{B}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}-\text{d}\unicode[STIX]{x1D6FD}/\text{d}x$
the magnetic curvature and
$\unicode[STIX]{x1D714}_{B}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}-\text{d}\unicode[STIX]{x1D6FD}/\text{d}x$
the magnetic curvature and
![]() $\unicode[STIX]{x1D735}B$
-drift frequencies, while
$\unicode[STIX]{x1D735}B$
-drift frequencies, while
![]() $L_{n}^{-1}=-n_{0}^{-1}\text{d}n_{0}/\text{d}x$
and
$L_{n}^{-1}=-n_{0}^{-1}\text{d}n_{0}/\text{d}x$
and
![]() $L_{T}^{-1}=-T_{i}^{-1}\text{d}T_{i}/\text{d}x$
define the characteristic density and temperature-gradient scales, and
$L_{T}^{-1}=-T_{i}^{-1}\text{d}T_{i}/\text{d}x$
define the characteristic density and temperature-gradient scales, and
![]() $\unicode[STIX]{x1D6FD}=8\unicode[STIX]{x03C0}n_{0}(T_{e}+T_{i})/B^{2}$
is the ratio of kinetic to magnetic pressure (which will shortly be set to zero),
$\unicode[STIX]{x1D6FD}=8\unicode[STIX]{x03C0}n_{0}(T_{e}+T_{i})/B^{2}$
is the ratio of kinetic to magnetic pressure (which will shortly be set to zero),
![]() $x$
is the radial coordinate and
$x$
is the radial coordinate and
![]() $y$
is a coordinate associated with the field-line labels on a magnetic surface. Notice that we are assuming
$y$
is a coordinate associated with the field-line labels on a magnetic surface. Notice that we are assuming
![]() $k_{x}=0$
for simplicity. The Bessel function squared originates, as usual, from a Fourier transform of the gyroaveraged potential followed by a
$k_{x}=0$
for simplicity. The Bessel function squared originates, as usual, from a Fourier transform of the gyroaveraged potential followed by a
![]() $\text{d}^{3}\boldsymbol{v}$
integral at constant
$\text{d}^{3}\boldsymbol{v}$
integral at constant
![]() $\boldsymbol{r}$
, the particle position. In (2.1) the eigenvalue
$\boldsymbol{r}$
, the particle position. In (2.1) the eigenvalue
![]() $\unicode[STIX]{x1D714}$
acquires non-zero imaginary values that regularise the, otherwise, singular integrand. The analytical form of the integral
$\unicode[STIX]{x1D714}$
acquires non-zero imaginary values that regularise the, otherwise, singular integrand. The analytical form of the integral
![]() $I_{i}$
for arbitrary Larmor radii is given in appendix A. The drift-kinetic limit is sufficient for the following discussion. In this case
$I_{i}$
for arbitrary Larmor radii is given in appendix A. The drift-kinetic limit is sufficient for the following discussion. In this case
![]() $\boldsymbol{k}_{\bot }\unicode[STIX]{x1D70C}_{i}\rightarrow 0$
,
$\boldsymbol{k}_{\bot }\unicode[STIX]{x1D70C}_{i}\rightarrow 0$
,
![]() $J_{0}^{2}\rightarrow 1$
, and it is easy to show that
$J_{0}^{2}\rightarrow 1$
, and it is easy to show that
 $$\begin{eqnarray}\displaystyle D & \equiv & \displaystyle -\left(1+\unicode[STIX]{x1D70F}\right)+I_{i}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle -\left(1+\unicode[STIX]{x1D70F}\right)+\left(1-\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\right)\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}Z^{2}\left(\sqrt{\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\unicode[STIX]{x1D702}_{i}\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\left\{\left(1-2\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}Z^{2}\left(\sqrt{\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}}\right)-2\left(\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)^{3/2}Z\left(\sqrt{\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}}\right)\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D & \equiv & \displaystyle -\left(1+\unicode[STIX]{x1D70F}\right)+I_{i}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle -\left(1+\unicode[STIX]{x1D70F}\right)+\left(1-\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\right)\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}Z^{2}\left(\sqrt{\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\unicode[STIX]{x1D702}_{i}\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\left\{\left(1-2\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}Z^{2}\left(\sqrt{\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}}\right)-2\left(\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)^{3/2}Z\left(\sqrt{\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}}\right)\right\},\end{eqnarray}$$
which corresponds to
![]() $D_{0}$
in (3) of BDR (Biglari et al.
Reference Biglari, Diamond and Rosenbluth1989). In the appendices we prove this result in two different ways; both are alternatives to the derivation of Biglari et al. (Reference Biglari, Diamond and Rosenbluth1989). The real frequency at marginality is evaluated by solving
$D_{0}$
in (3) of BDR (Biglari et al.
Reference Biglari, Diamond and Rosenbluth1989). In the appendices we prove this result in two different ways; both are alternatives to the derivation of Biglari et al. (Reference Biglari, Diamond and Rosenbluth1989). The real frequency at marginality is evaluated by solving
![]() $\text{Im}[D(\unicode[STIX]{x1D714}_{r})]\equiv D_{i}(\unicode[STIX]{x1D714}_{r})=0$
, where one sets
$\text{Im}[D(\unicode[STIX]{x1D714}_{r})]\equiv D_{i}(\unicode[STIX]{x1D714}_{r})=0$
, where one sets
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D6FE}$
, and takes
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D6FE}$
, and takes
![]() $\unicode[STIX]{x1D6FE}\rightarrow 0$
. Using (2.5) this means
$\unicode[STIX]{x1D6FE}\rightarrow 0$
. Using (2.5) this means
Once
![]() $\unicode[STIX]{x1D714}_{r}$
is found, the condition that determines destabilisation is
$\unicode[STIX]{x1D714}_{r}$
is found, the condition that determines destabilisation is
![]() $\text{Re}[D(\unicode[STIX]{x1D714}_{r})]>0$
, which can be determined only numerically. However, Romanelli (Romanelli Reference Romanelli1989) has evaluated the integral
$\text{Re}[D(\unicode[STIX]{x1D714}_{r})]>0$
, which can be determined only numerically. However, Romanelli (Romanelli Reference Romanelli1989) has evaluated the integral
![]() $I_{i}$
by replacing
$I_{i}$
by replacing
![]() $v_{\bot }^{2}/2+v_{\Vert }^{2}\rightarrow 4/3(v_{\bot }^{2}+v_{\Vert }^{2})$
in the definition of the particle magnetic drifts (see (2.4)) in order to fit the numerical solution of (2.1) at
$v_{\bot }^{2}/2+v_{\Vert }^{2}\rightarrow 4/3(v_{\bot }^{2}+v_{\Vert }^{2})$
in the definition of the particle magnetic drifts (see (2.4)) in order to fit the numerical solution of (2.1) at
![]() $R/L_{n}\ll 1$
, for
$R/L_{n}\ll 1$
, for
![]() $k_{y}\unicode[STIX]{x1D70C}_{s}=\sqrt{0.1}\approx 0.32$
, where
$k_{y}\unicode[STIX]{x1D70C}_{s}=\sqrt{0.1}\approx 0.32$
, where
![]() $\unicode[STIX]{x1D70C}_{s}=\sqrt{T_{i}/m_{i}}/\unicode[STIX]{x1D6FA}_{i}=\unicode[STIX]{x1D70C}_{i}/\sqrt{2}$
. In his case, the condition
$\unicode[STIX]{x1D70C}_{s}=\sqrt{T_{i}/m_{i}}/\unicode[STIX]{x1D6FA}_{i}=\unicode[STIX]{x1D70C}_{i}/\sqrt{2}$
. In his case, the condition
![]() $\text{Re}[D(\unicode[STIX]{x1D714}_{r})]>0$
yields a critical gradient
$\text{Re}[D(\unicode[STIX]{x1D714}_{r})]>0$
yields a critical gradient
![]() $\left.R/L_{T}\right|_{\text{crit}}=(1+\unicode[STIX]{x1D70F})(4/3)$
whose
$\left.R/L_{T}\right|_{\text{crit}}=(1+\unicode[STIX]{x1D70F})(4/3)$
whose
![]() $\unicode[STIX]{x1D70F}$
dependence comes from the obvious fact that
$\unicode[STIX]{x1D70F}$
dependence comes from the obvious fact that
![]() $\text{Re}[D(\unicode[STIX]{x1D714}_{r})]>0$
implies
$\text{Re}[D(\unicode[STIX]{x1D714}_{r})]>0$
implies
![]() $\text{Re}[I_{i}(\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r})]>1+\unicode[STIX]{x1D70F}$
. Obtaining the correct mode frequency at marginality is therefore crucial. From direct numerical simulations we see that this quantity shows a dependence on the ion temperature that is not captured by Romanelli’s treatment, nor by any other analytical theory known to us (see figure 1).
$\text{Re}[I_{i}(\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r})]>1+\unicode[STIX]{x1D70F}$
. Obtaining the correct mode frequency at marginality is therefore crucial. From direct numerical simulations we see that this quantity shows a dependence on the ion temperature that is not captured by Romanelli’s treatment, nor by any other analytical theory known to us (see figure 1).

Figure 1. Real frequency from the GENE code as a function of the temperature gradient for different
![]() $\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
. The
$\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
. The
![]() $\unicode[STIX]{x1D70F}$
dependence is evident. Cyclone base case parameters are used (see text for details).
$\unicode[STIX]{x1D70F}$
dependence is evident. Cyclone base case parameters are used (see text for details).
In our numerical tests, we consider adiabatic electrons and typical cyclone base case (CBC) parameters for
![]() ${\hat{s}}-\unicode[STIX]{x1D6FC}$
geometry:
${\hat{s}}-\unicode[STIX]{x1D6FC}$
geometry:
![]() ${\hat{s}}=0.786$
,
${\hat{s}}=0.786$
,
![]() $q=\unicode[STIX]{x1D704}^{-1}=1.4$
,
$q=\unicode[STIX]{x1D704}^{-1}=1.4$
,
![]() $\unicode[STIX]{x1D716}=r/R=0.18$
,
$\unicode[STIX]{x1D716}=r/R=0.18$
,
![]() $R/L_{n}=2$
,
$R/L_{n}=2$
,
![]() $k_{y}\unicode[STIX]{x1D70C}_{s}=0.3$
, where
$k_{y}\unicode[STIX]{x1D70C}_{s}=0.3$
, where
![]() $R$
is the device major radius. From the imaginary part of the eigenvalue, we extract the critical gradient (see figure 2). Figure 3 shows the resulting critical gradient compared to several theories and one fitting formula. The linear fit of the numerical data givesFootnote
3
$R$
is the device major radius. From the imaginary part of the eigenvalue, we extract the critical gradient (see figure 2). Figure 3 shows the resulting critical gradient compared to several theories and one fitting formula. The linear fit of the numerical data givesFootnote
3
![]() $\left.R/L_{T}\right|_{\text{crit}}=(2.45\pm 0.07)\unicode[STIX]{x1D70F}+2.07\pm 0.06$
, with a reduced
$\left.R/L_{T}\right|_{\text{crit}}=(2.45\pm 0.07)\unicode[STIX]{x1D70F}+2.07\pm 0.06$
, with a reduced
![]() $\unicode[STIX]{x1D712}^{2}=6.5\times 10^{-4}$
. The fitting formula of Jenko et al. (Reference Jenko, Dorland and Hammett2001) (hereafter denoted by JDH) is
$\unicode[STIX]{x1D712}^{2}=6.5\times 10^{-4}$
. The fitting formula of Jenko et al. (Reference Jenko, Dorland and Hammett2001) (hereafter denoted by JDH) is
![]() $\left.R/L_{T}\right|_{\text{crit}}=(1+\unicode[STIX]{x1D70F})(4/3+1.91\,{\hat{s}}/q)$
. The curve derived by Romanelli (Reference Romanelli1989),
$\left.R/L_{T}\right|_{\text{crit}}=(1+\unicode[STIX]{x1D70F})(4/3+1.91\,{\hat{s}}/q)$
. The curve derived by Romanelli (Reference Romanelli1989),
![]() $R/L_{T}=(1+\unicode[STIX]{x1D70F})\left(4/3\right)$
, which should work better for flat densities,
$R/L_{T}=(1+\unicode[STIX]{x1D70F})\left(4/3\right)$
, which should work better for flat densities,
![]() $R/L_{n}\rightarrow 0$
, is not expected to match the numerical results for
$R/L_{n}\rightarrow 0$
, is not expected to match the numerical results for
![]() $R/L_{n}=2$
,
$R/L_{n}=2$
,
![]() $R/L_{T}=O(1)$
, even if
$R/L_{T}=O(1)$
, even if
![]() $q\rightarrow \infty$
(in which case the streaming term effect measured by the factor
$q\rightarrow \infty$
(in which case the streaming term effect measured by the factor
![]() ${\hat{s}}/q$
in the JDH formula should be negligible, as it is neglected in (2.1)). The BDR condition for destabilisation (Biglari et al.
Reference Biglari, Diamond and Rosenbluth1989) would give
${\hat{s}}/q$
in the JDH formula should be negligible, as it is neglected in (2.1)). The BDR condition for destabilisation (Biglari et al.
Reference Biglari, Diamond and Rosenbluth1989) would give
![]() $R/L_{T}=2.7$
, with virtually no dependence on
$R/L_{T}=2.7$
, with virtually no dependence on
![]() $\unicode[STIX]{x1D70F}$
. The full ion Larmor radius resonant theory developed in the present article predicts higher critical gradients than the long-wavelength resonant theory. Like results from numerical simulations, it gives a critical gradient that depends linearly on
$\unicode[STIX]{x1D70F}$
. The full ion Larmor radius resonant theory developed in the present article predicts higher critical gradients than the long-wavelength resonant theory. Like results from numerical simulations, it gives a critical gradient that depends linearly on
![]() $\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
, but it underestimates the numerical results. As already mentioned, this discrepancy can be attributed to the fact that analytical theories predict a real frequency at marginality that does not depend on
$\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
, but it underestimates the numerical results. As already mentioned, this discrepancy can be attributed to the fact that analytical theories predict a real frequency at marginality that does not depend on
![]() $\unicode[STIX]{x1D70F}$
, as opposed to the numerical findings. This is true for all the analytical theories revisited and derived here, and seems to be a consequence of the neglect in (2.1) of the streaming term. The problem is, of course, that parallel streaming has been neglected in the derivation of (2.1), which can only be satisfied at a single (or a pair of) poloidal location on the flux surface. Taken literally, this equation thus implies that the entire mode structure is concentrated at this point, which, in the analytical theories quoted, is the location where the field curvature is most unfavourable. However, in all practical circumstances, that is not what the mode structure is, and the streaming term (with its
$\unicode[STIX]{x1D70F}$
, as opposed to the numerical findings. This is true for all the analytical theories revisited and derived here, and seems to be a consequence of the neglect in (2.1) of the streaming term. The problem is, of course, that parallel streaming has been neglected in the derivation of (2.1), which can only be satisfied at a single (or a pair of) poloidal location on the flux surface. Taken literally, this equation thus implies that the entire mode structure is concentrated at this point, which, in the analytical theories quoted, is the location where the field curvature is most unfavourable. However, in all practical circumstances, that is not what the mode structure is, and the streaming term (with its
![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}$
derivatives, where
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}$
derivatives, where
![]() $\unicode[STIX]{x1D703}$
is the ballooning angle) determines the rate at which the eigenmode decays along the field line.
$\unicode[STIX]{x1D703}$
is the ballooning angle) determines the rate at which the eigenmode decays along the field line.

Figure 2. Growth rate from the GENE code as a function of the temperature gradient for different
![]() $\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
. The
$\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
. The
![]() $\unicode[STIX]{x1D70F}$
dependence is evident. CBC parameters are used (see text for details).
$\unicode[STIX]{x1D70F}$
dependence is evident. CBC parameters are used (see text for details).

Figure 3. Critical threshold from GENE data, linear fit to GENE data, fitting formula of Jenko Dorland and Hammett and different local theories. The GENE data at
![]() $q=100$
should be compared to the local theories.
$q=100$
should be compared to the local theories.
The results from GENE simulations are somewhat consistent with the fitting formula of Jenko et al. (Reference Jenko, Dorland and Hammett2001) (hereafter JDH) but do not seem to relate to the theory of Hahm & Tang (Reference Hahm and Tang1989), since we find a stabilising contribution from finite shear. This is in line with a statement present in the work of Biglari et al. (Reference Biglari, Diamond and Rosenbluth1989).Footnote
4
The remaining two curves are derived from the numerical solution of the dispersion relation with full Larmor orbits, equation (A 1), for small (
![]() $\boldsymbol{k}_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$
) and for arbitrary Larmor radii. Strictly speaking, all our numerical results are valid for one specific wavelength:
$\boldsymbol{k}_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$
) and for arbitrary Larmor radii. Strictly speaking, all our numerical results are valid for one specific wavelength:
![]() $k_{y}\unicode[STIX]{x1D70C}_{s}=0.3$
. However, a dependence of the numerical results on
$k_{y}\unicode[STIX]{x1D70C}_{s}=0.3$
. However, a dependence of the numerical results on
![]() $k_{y}$
cannot be excluded. A sensitivity scan was performed for the reference value
$k_{y}$
cannot be excluded. A sensitivity scan was performed for the reference value
![]() $\unicode[STIX]{x1D70F}=1$
. If we vary
$\unicode[STIX]{x1D70F}=1$
. If we vary
![]() $0.2\leqslant k_{y}\unicode[STIX]{x1D70C}_{s}\leqslant 0.4$
, we find a critical gradient in the range
$0.2\leqslant k_{y}\unicode[STIX]{x1D70C}_{s}\leqslant 0.4$
, we find a critical gradient in the range
![]() $4.35\leqslant \left.R/L_{T}\right|_{\text{crit}}\leqslant 4.8$
This indeterminacy is small enough to discriminate the analytical results of figure 3, and large enough to let us consider the JDH formula quite reliable.
$4.35\leqslant \left.R/L_{T}\right|_{\text{crit}}\leqslant 4.8$
This indeterminacy is small enough to discriminate the analytical results of figure 3, and large enough to let us consider the JDH formula quite reliable.
This preliminary analysis is in fact more general that it would seem. Equations (2.1) and (A 1) were derived by neglecting the contribution associated with particle streaming, but the magnetic drift frequencies
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
and
![]() $\unicode[STIX]{x1D714}_{B}$
are essentially arbitrary. They must therefore be applicable to the stellarator case as well. There is a key factor that now brings tokamaks and stellarators together. A low-bootstrap-current stellarator, such as Wendelstein 7-X, possesses a low global shear. This condition is, incidentally, the same condition that is required to neglect particle streaming in the kinetic equation, and the slab branch of the ITG instability (Jenko et al.
Reference Jenko, Dorland and Hammett2001) for the tokamak case. Thus, for low shear, the resonant destabilisation of the ITG mode in tokamaks and stellarators could show some common features. In the following sections we will discover what these common aspects are.
$\unicode[STIX]{x1D714}_{B}$
are essentially arbitrary. They must therefore be applicable to the stellarator case as well. There is a key factor that now brings tokamaks and stellarators together. A low-bootstrap-current stellarator, such as Wendelstein 7-X, possesses a low global shear. This condition is, incidentally, the same condition that is required to neglect particle streaming in the kinetic equation, and the slab branch of the ITG instability (Jenko et al.
Reference Jenko, Dorland and Hammett2001) for the tokamak case. Thus, for low shear, the resonant destabilisation of the ITG mode in tokamaks and stellarators could show some common features. In the following sections we will discover what these common aspects are.

Figure 4. Imaginary part of eigenvalue from the GENE code as a function of the temperature gradient for different
![]() $\unicode[STIX]{x1D70F}$
. Parameters as in figure 1, but
$\unicode[STIX]{x1D70F}$
. Parameters as in figure 1, but
![]() ${\hat{s}}=0.1$
,
${\hat{s}}=0.1$
,
![]() $\unicode[STIX]{x1D716}=0.03$
. The ‘background’ modes at marginality are evident.
$\unicode[STIX]{x1D716}=0.03$
. The ‘background’ modes at marginality are evident.

Figure 5. Real part of eigenvalue from the GENE code as a function of the temperature gradient for different
![]() $\unicode[STIX]{x1D70F}$
. Parameters as in figure 1, but
$\unicode[STIX]{x1D70F}$
. Parameters as in figure 1, but
![]() ${\hat{s}}=0.1$
,
${\hat{s}}=0.1$
,
![]() $\unicode[STIX]{x1D716}=0.03$
. The ‘background’ modes at marginality are evident.
$\unicode[STIX]{x1D716}=0.03$
. The ‘background’ modes at marginality are evident.

Figure 6. Ion distribution function in phase space.
![]() $\unicode[STIX]{x1D70F}=1$
,
$\unicode[STIX]{x1D70F}=1$
,
![]() $R/L_{T}=3$
, for the ‘background’ mode that belongs to the ‘foot’ of figure 5. No clear resonance at finite
$R/L_{T}=3$
, for the ‘background’ mode that belongs to the ‘foot’ of figure 5. No clear resonance at finite
![]() $v_{\Vert }$
. The velocity-space resolution in the
$v_{\Vert }$
. The velocity-space resolution in the
![]() $v_{\Vert }$
-direction is
$v_{\Vert }$
-direction is
![]() $5.86\times 10^{-3}$
. Other parameters as in figure 5.
$5.86\times 10^{-3}$
. Other parameters as in figure 5.

Figure 7. Ion distribution function in phase space.
![]() $\unicode[STIX]{x1D70F}=1$
,
$\unicode[STIX]{x1D70F}=1$
,
![]() $R/L_{T}=5$
, for the toroidal branch mode. Resonance occurs outside the
$R/L_{T}=5$
, for the toroidal branch mode. Resonance occurs outside the
![]() $\unicode[STIX]{x1D707}\pm \hat{v}_{\Vert }^{2}\equiv \text{const.}$
boundary. The velocity-space resolution in the
$\unicode[STIX]{x1D707}\pm \hat{v}_{\Vert }^{2}\equiv \text{const.}$
boundary. The velocity-space resolution in the
![]() $v_{\Vert }$
-direction is
$v_{\Vert }$
-direction is
![]() $5.86\times 10^{-3}$
. Other parameters as in figure 5.
$5.86\times 10^{-3}$
. Other parameters as in figure 5.

Figure 8. Eigenfunctions as a function of the ballooning angle for the
![]() ${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak equilibrium from the GENE code (flux tube). Here
${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak equilibrium from the GENE code (flux tube). Here
![]() $\unicode[STIX]{x1D70F}=1$
,
$\unicode[STIX]{x1D70F}=1$
,
![]() $k_{y}\unicode[STIX]{x1D70C}_{s}=0.3$
,
$k_{y}\unicode[STIX]{x1D70C}_{s}=0.3$
,
![]() $a/L_{T}=3$
(Floquet),
$a/L_{T}=3$
(Floquet),
![]() $a/L_{T}=5$
(toroidal branch). The velocity-space resolution in the
$a/L_{T}=5$
(toroidal branch). The velocity-space resolution in the
![]() $v_{\Vert }$
direction is
$v_{\Vert }$
direction is
![]() $5.86\times 10^{-3}$
. Other parameters as in figure 4.
$5.86\times 10^{-3}$
. Other parameters as in figure 4.

Figure 9. A ‘zoom’ of figure 8. Eigenfunctions as a function of the ballooning angle for the
![]() ${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak equilibrium from the GENE code (flux tube). Here
${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak equilibrium from the GENE code (flux tube). Here
![]() $\unicode[STIX]{x1D70F}=1$
,
$\unicode[STIX]{x1D70F}=1$
,
![]() $k_{y}\unicode[STIX]{x1D70C}_{s}=0.3$
,
$k_{y}\unicode[STIX]{x1D70C}_{s}=0.3$
,
![]() $a/L_{T}=3$
(Floquet),
$a/L_{T}=3$
(Floquet),
![]() $a/L_{T}=5$
(toroidal branch). The velocity-space resolution in the
$a/L_{T}=5$
(toroidal branch). The velocity-space resolution in the
![]() $v_{\Vert }$
direction is
$v_{\Vert }$
direction is
![]() $5.86\times 10^{-3}$
.
$5.86\times 10^{-3}$
.
2.1 Low-shear tokamak
We repeat the same study that was performed above to benchmark the analytical theories of the destabilisation of the toroidal ITG, but for
![]() ${\hat{s}}=0.1$
, and
${\hat{s}}=0.1$
, and
![]() $\unicode[STIX]{x1D716}=0.03$
, instead of
$\unicode[STIX]{x1D716}=0.03$
, instead of
![]() ${\hat{s}}=0.768$
and
${\hat{s}}=0.768$
and
![]() $\unicode[STIX]{x1D716}=0.18$
. The results are shown in figures (4)–(5), and exhibit a new family of unstable modes below what would have been the critical gradient had we extrapolated to
$\unicode[STIX]{x1D716}=0.18$
. The results are shown in figures (4)–(5), and exhibit a new family of unstable modes below what would have been the critical gradient had we extrapolated to
![]() $\unicode[STIX]{x1D6FE}\rightarrow 0$
the growth rate calculated at large
$\unicode[STIX]{x1D6FE}\rightarrow 0$
the growth rate calculated at large
![]() $R/L_{T}$
. These modes behave as a persistent ‘background’ of instability. The velocity-space structures and the eigenfunctions of two representative modes (one from the ‘background’, one from the strongly driven toroidal branch) are compared in figures 6 and 7. For these cases, a velocity-space resolution of
$R/L_{T}$
. These modes behave as a persistent ‘background’ of instability. The velocity-space structures and the eigenfunctions of two representative modes (one from the ‘background’, one from the strongly driven toroidal branch) are compared in figures 6 and 7. For these cases, a velocity-space resolution of
![]() $\text{lv}/\text{nv0}=3/512\approx 5.86\times 10^{-3}$
, where lv is the extension of the simulation box (in units of thermal speed), and nv0 is the number of grid points in the
$\text{lv}/\text{nv0}=3/512\approx 5.86\times 10^{-3}$
, where lv is the extension of the simulation box (in units of thermal speed), and nv0 is the number of grid points in the
![]() $v_{\Vert }$
- direction, was required to fully resolve the maximum of the distribution function of the background mode at
$v_{\Vert }$
- direction, was required to fully resolve the maximum of the distribution function of the background mode at
![]() $v_{\Vert }=0$
. However, the eigenvalue would not be affected by choosing slightly larger values. All other resolutions are kept consistent with the analysis of the previous section, but care must be taken to fully resolve the asymptotic behaviour of the ‘background’ mode eigenfunctions for large ballooning angles. Since, formally, the ballooning angle is the Fourier conjugate of the local radial variable, asymptotically decaying eigenfunctions are captured by increasing the radial resolution. In our case, for a domain
$v_{\Vert }=0$
. However, the eigenvalue would not be affected by choosing slightly larger values. All other resolutions are kept consistent with the analysis of the previous section, but care must be taken to fully resolve the asymptotic behaviour of the ‘background’ mode eigenfunctions for large ballooning angles. Since, formally, the ballooning angle is the Fourier conjugate of the local radial variable, asymptotically decaying eigenfunctions are captured by increasing the radial resolution. In our case, for a domain
![]() $L_{x}=1/(k_{y}\unicode[STIX]{x1D70C}_{s}{\hat{s}})\approx 33.33$
, the number of grid points in the radial (
$L_{x}=1/(k_{y}\unicode[STIX]{x1D70C}_{s}{\hat{s}})\approx 33.33$
, the number of grid points in the radial (
![]() $x$
) direction varies from
$x$
) direction varies from
![]() $24$
to
$24$
to
![]() $64$
. A comparison of the eigenfunctions for the two types of modes is in figures 8 and 9. From the first, we see that, at marginality, both eigenfunctions decay rather slowly. However, the decay length of the background mode is much greater. Furthermore, the background mode does not have an absolute maximum at
$64$
. A comparison of the eigenfunctions for the two types of modes is in figures 8 and 9. From the first, we see that, at marginality, both eigenfunctions decay rather slowly. However, the decay length of the background mode is much greater. Furthermore, the background mode does not have an absolute maximum at
![]() $\unicode[STIX]{x1D703}=0$
. While the strongly driven mode shows resonances at finite
$\unicode[STIX]{x1D703}=0$
. While the strongly driven mode shows resonances at finite
![]() $v_{\Vert }$
outside the
$v_{\Vert }$
outside the
![]() $\unicode[STIX]{x1D707}\pm \hat{v}_{\Vert }^{2}\equiv \text{const.}$
boundary, the background mode does not show structure at finite
$\unicode[STIX]{x1D707}\pm \hat{v}_{\Vert }^{2}\equiv \text{const.}$
boundary, the background mode does not show structure at finite
![]() $v_{\Vert }$
. Its dependence on the inverse aspect ratio is shown in figure 10. We see that the slab character of the instability is more pronounced for larger aspect ratios. It is of some interest to know whether, for a given aspect ratio, there is a critical shear,
$v_{\Vert }$
. Its dependence on the inverse aspect ratio is shown in figure 10. We see that the slab character of the instability is more pronounced for larger aspect ratios. It is of some interest to know whether, for a given aspect ratio, there is a critical shear,
![]() ${\hat{s}}_{\text{crit}}$
, above which the ‘background’ modes are suppressed. For the case
${\hat{s}}_{\text{crit}}$
, above which the ‘background’ modes are suppressed. For the case
![]() $R/L_{T}=3$
, and
$R/L_{T}=3$
, and
![]() $\unicode[STIX]{x1D716}=0.18$
of figure 10, we find
$\unicode[STIX]{x1D716}=0.18$
of figure 10, we find
![]() $0.14<{\hat{s}}_{\text{crit}}<0.16$
. For flat density profiles,
$0.14<{\hat{s}}_{\text{crit}}<0.16$
. For flat density profiles,
![]() $R/L_{n}=0$
, and moderate inverse aspect ratio,
$R/L_{n}=0$
, and moderate inverse aspect ratio,
![]() $\unicode[STIX]{x1D716}=0.18$
, the real frequency at marginality shows an even stronger dependence on the temperature ratio,
$\unicode[STIX]{x1D716}=0.18$
, the real frequency at marginality shows an even stronger dependence on the temperature ratio,
![]() $\unicode[STIX]{x1D70F}$
, (figure 11) but, for the specific parameters used, the background modes are not present. The equilibrium values chosen to let the background modes emerge could seem unrealistic. Let us therefore consider a situation where such modes are always expected, almost by design.
$\unicode[STIX]{x1D70F}$
, (figure 11) but, for the specific parameters used, the background modes are not present. The equilibrium values chosen to let the background modes emerge could seem unrealistic. Let us therefore consider a situation where such modes are always expected, almost by design.

Figure 10. A ‘zoom’ of the low shear,
![]() ${\hat{s}}=0.1$
, ‘background’ marginal modes for
${\hat{s}}=0.1$
, ‘background’ marginal modes for
![]() $\unicode[STIX]{x1D70F}=1$
for several inverse aspect ratios.
$\unicode[STIX]{x1D70F}=1$
for several inverse aspect ratios.
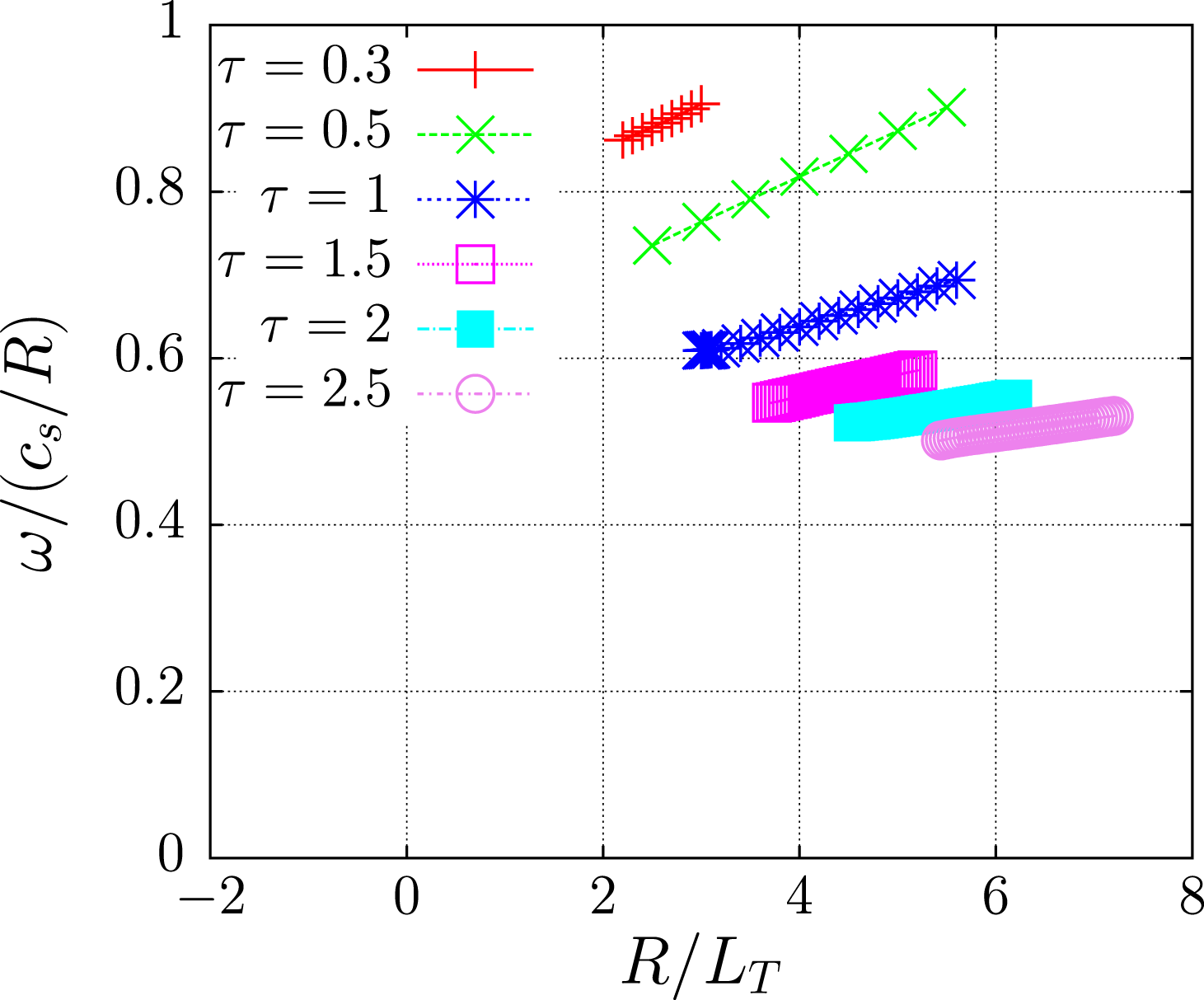
Figure 11. Real part of eigenvalue from the GENE code as a function of the temperature gradient for different
![]() $\unicode[STIX]{x1D70F}$
. Parameters as in figure 1, but
$\unicode[STIX]{x1D70F}$
. Parameters as in figure 1, but
![]() ${\hat{s}}=0.1$
and
${\hat{s}}=0.1$
and
![]() $R/L_{n}=0$
. The
$R/L_{n}=0$
. The
![]() $\unicode[STIX]{x1D70F}$
dependence at marginality is evident.
$\unicode[STIX]{x1D70F}$
dependence at marginality is evident.
2.2 Wendelstein 7-X
The stellarator Wendelstein 7-X shows the same qualitative behaviour as just described for the tokamak case. We consider a high-mirror configuration (Geiger et al.
Reference Geiger, Beidler, Feng, Maassberg, Marushchenko and Turkin2015) at a normalised radial position
![]() $r/a=0.7$
, for
$r/a=0.7$
, for
![]() $k_{y}\unicode[STIX]{x1D70C}_{s}=0.9$
, flat density
$k_{y}\unicode[STIX]{x1D70C}_{s}=0.9$
, flat density
![]() $a/L_{n}=0$
,
$a/L_{n}=0$
,
![]() $q=1/\unicode[STIX]{x1D704}=1.10186$
and small negative global shear
$q=1/\unicode[STIX]{x1D704}=1.10186$
and small negative global shear
![]() ${\hat{s}}=-0.1286$
. Here
${\hat{s}}=-0.1286$
. Here
![]() $a$
is the average minor radius. Such configuration can be considered to be ‘standard’. It is realised by setting to zero the current in the planar coils, and imposing a ‘large’ ratio of average toroidal to helical curvature,
$a$
is the average minor radius. Such configuration can be considered to be ‘standard’. It is realised by setting to zero the current in the planar coils, and imposing a ‘large’ ratio of average toroidal to helical curvature,
![]() $b_{1,0}/b_{1,1}\approx 0.5$
, and a finite-mirror term,
$b_{1,0}/b_{1,1}\approx 0.5$
, and a finite-mirror term,
![]() $b_{0,1}\approx 0.1$
, where
$b_{0,1}\approx 0.1$
, where
![]() $b_{n,m}$
are the Fourier components of the equilibrium magnetic field in Boozer coordinates (Xanthopoulos et al.
Reference Xanthopoulos, Cooper, Jenko, Turkin, Runov and Geiger2009). A scan in normalised temperature-gradient scale,
$b_{n,m}$
are the Fourier components of the equilibrium magnetic field in Boozer coordinates (Xanthopoulos et al.
Reference Xanthopoulos, Cooper, Jenko, Turkin, Runov and Geiger2009). A scan in normalised temperature-gradient scale,
![]() $a/L_{T}$
, is given in figures 12 and 13 for several
$a/L_{T}$
, is given in figures 12 and 13 for several
![]() $\unicode[STIX]{x1D70F}$
. As in the tokamak case, there is a background of unstable modes below the threshold of the strongly driven toroidal ITG branch. An inspection of the real part of the eigenvalue reveals more frequent, but milder, jumps than in the tokamak case. The eigenfunction is plotted in figure 14 for
$\unicode[STIX]{x1D70F}$
. As in the tokamak case, there is a background of unstable modes below the threshold of the strongly driven toroidal ITG branch. An inspection of the real part of the eigenvalue reveals more frequent, but milder, jumps than in the tokamak case. The eigenfunction is plotted in figure 14 for
![]() $a/L_{T}=0.8$
(background) and
$a/L_{T}=0.8$
(background) and
![]() $a/L_{T}=3$
. (toroidal branch) for
$a/L_{T}=3$
. (toroidal branch) for
![]() $\unicode[STIX]{x1D70F}=1$
. The global shear is kept constant, the mode localisation of the two modes is very different: the background mode shows a much slower variation along the field-line-following coordinate than the toroidal branch mode. Our results suggest that the linear threshold for destabilisation of ITG modes in Wendelstein 7-X could be overestimated by a rough extrapolation of the toroidal branch to
$\unicode[STIX]{x1D70F}=1$
. The global shear is kept constant, the mode localisation of the two modes is very different: the background mode shows a much slower variation along the field-line-following coordinate than the toroidal branch mode. Our results suggest that the linear threshold for destabilisation of ITG modes in Wendelstein 7-X could be overestimated by a rough extrapolation of the toroidal branch to
![]() $\unicode[STIX]{x1D6FE}\rightarrow 0$
, even for flat densities.
$\unicode[STIX]{x1D6FE}\rightarrow 0$
, even for flat densities.

Figure 12. Growth rate of microinstability in Wendelstein 7-X from the GENE code (flux tube). High-mirror configuration, adiabatic electrons, radial position
![]() $r/a=0.7$
. The ‘background’ modes at marginality are evident.
$r/a=0.7$
. The ‘background’ modes at marginality are evident.

Figure 13. Frequency associated with the unstable modes of figure 12 evaluated for Wendelstein 7-X from the GENE code (flux tube). High-mirror configuration, adiabatic electrons, radial position
![]() $r/a=0.7$
, for
$r/a=0.7$
, for
![]() $k_{y}\unicode[STIX]{x1D70C}_{s}=0.9$
.
$k_{y}\unicode[STIX]{x1D70C}_{s}=0.9$
.

Figure 14. Eigenfunctions for Wendelstein 7-X from the GENE code (flux tube). High-mirror configuration, adiabatic electrons, radial position
![]() $r/a=0.7$
. Here
$r/a=0.7$
. Here
![]() $\unicode[STIX]{x1D70F}=1$
,
$\unicode[STIX]{x1D70F}=1$
,
![]() $k_{y}\unicode[STIX]{x1D70C}_{s}=0.9$
,
$k_{y}\unicode[STIX]{x1D70C}_{s}=0.9$
,
![]() $a/L_{T}=0.8$
(Floquet),
$a/L_{T}=0.8$
(Floquet),
![]() $a/L_{T}=3$
(toroidal branch).
$a/L_{T}=3$
(toroidal branch).
3 Temperature dependence of critical thresholds
In the previous section we have conjectured that the resonant destabilisation of the ITG mode in low-shear tokamaks and stellarators possesses common features. Numerical simulations corroborate this hypothesis. We refrain from proposing some universal formula for critical gradients at low shear, nonetheless we find it instructive to explore the temperature dependence of the critical gradient, since this puts the new results in the same context as previous analytical studies.
In the asymptotic limit of large inverse aspect ratio,
![]() $\unicode[STIX]{x1D716}=0.03$
, the
$\unicode[STIX]{x1D716}=0.03$
, the
![]() ${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak case gives a critical inverse gradient that increases with
${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak case gives a critical inverse gradient that increases with
![]() $\unicode[STIX]{x1D70F}$
, for
$\unicode[STIX]{x1D70F}$
, for
![]() $\unicode[STIX]{x1D70F}\gtrsim 1$
. For
$\unicode[STIX]{x1D70F}\gtrsim 1$
. For
![]() $\unicode[STIX]{x1D70F}\lesssim 1$
, the instability threshold is fixed by the density gradient, e.g.
$\unicode[STIX]{x1D70F}\lesssim 1$
, the instability threshold is fixed by the density gradient, e.g.
![]() $(R/L_{T})_{\text{crit}}\approx R/L_{n}$
(see figure 15). In accordance with the JDH formula, a decreasing shear and an increasing
$(R/L_{T})_{\text{crit}}\approx R/L_{n}$
(see figure 15). In accordance with the JDH formula, a decreasing shear and an increasing
![]() $L_{n}/L_{T}$
have a destabilising effect (see figure 16). The results for Wendelstein 7-X (figure 17) were all derived in the flat density limit
$L_{n}/L_{T}$
have a destabilising effect (see figure 16). The results for Wendelstein 7-X (figure 17) were all derived in the flat density limit
![]() $R/L_{n}=0$
. The critical temperature gradient is a growing function of
$R/L_{n}=0$
. The critical temperature gradient is a growing function of
![]() $\unicode[STIX]{x1D70F}$
. We observe that
$\unicode[STIX]{x1D70F}$
. We observe that
![]() $(a/L_{T})_{\text{crit}}\approx 1$
for sufficiently hot ions,
$(a/L_{T})_{\text{crit}}\approx 1$
for sufficiently hot ions,
![]() $\unicode[STIX]{x1D70F}\gtrsim 2$
.
$\unicode[STIX]{x1D70F}\gtrsim 2$
.

Figure 15. Critical threshold from GENE data of figure 5 for several density gradients,
![]() $R/L_{n}.$
$R/L_{n}.$

Figure 16. Critical threshold from GENE. CBC parameters are used (see text for details), however
![]() ${\hat{s}}=0.1$
for
${\hat{s}}=0.1$
for
![]() $R/L_{n}=0$
and
$R/L_{n}=0$
and
![]() ${\hat{s}}=0.786$
for
${\hat{s}}=0.786$
for
![]() $R/L_{n}=2$
.
$R/L_{n}=2$
.

Figure 17. Critical gradient for Wendelstein
![]() $7-X$
as a function of the temperature ratio
$7-X$
as a function of the temperature ratio
![]() $\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
.
$\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
.
4 Floquet solutions
What are the modes that emerge below the critical threshold of the toroidal branch at low shear? In the classical nomenclature of ITG modes in tokamaks, for
![]() ${\hat{s}}/q\approx \unicode[STIX]{x1D704}{\hat{s}}\ll 1$
, the slab branch of the instability tends to be negligible. Below marginality the toroidal branch is stable. We saw that the background of modes at marginality is not eliminated at large inverse aspect ratios in tokamaks. High-mirror, as well as low-mirror, Wendelstein 7-X configurations also exhibit this persistent feature, and we recall that density gradients are stabilising since the electrons are taken to be adiabatic. To shed some light on the nature of these modes, we are compelled to abandon for a moment the regime of marginality and consider these modes at their maximum growth rate. We first verify where this maximum is. We select two representative cases for
${\hat{s}}/q\approx \unicode[STIX]{x1D704}{\hat{s}}\ll 1$
, the slab branch of the instability tends to be negligible. Below marginality the toroidal branch is stable. We saw that the background of modes at marginality is not eliminated at large inverse aspect ratios in tokamaks. High-mirror, as well as low-mirror, Wendelstein 7-X configurations also exhibit this persistent feature, and we recall that density gradients are stabilising since the electrons are taken to be adiabatic. To shed some light on the nature of these modes, we are compelled to abandon for a moment the regime of marginality and consider these modes at their maximum growth rate. We first verify where this maximum is. We select two representative cases for
![]() $\unicode[STIX]{x1D716}=0.1$
, and
$\unicode[STIX]{x1D716}=0.1$
, and
![]() $\unicode[STIX]{x1D70F}=1:$
$\unicode[STIX]{x1D70F}=1:$
![]() $R/L_{T}=3$
(background) and
$R/L_{T}=3$
(background) and
![]() $R/L_{T}=4$
(strong toroidal branch). The spectra of the two instabilities are shown in figure 18. We first notice that both the background and toroidal branch modes occur approximately at the same ion scale,
$R/L_{T}=4$
(strong toroidal branch). The spectra of the two instabilities are shown in figure 18. We first notice that both the background and toroidal branch modes occur approximately at the same ion scale,
![]() $k_{y}\unicode[STIX]{x1D70C}_{s}\approx 0.3$
. This does not necessarily imply that the two modes would be destabilised for the same
$k_{y}\unicode[STIX]{x1D70C}_{s}\approx 0.3$
. This does not necessarily imply that the two modes would be destabilised for the same
![]() $R/L_{T}$
. Let us now consider the non-resonant limit. We take the fluid limit of the ITG equation (see (19) of Zocco et al. (Reference Zocco, Plunk, Xanthopoulos and Helander2016), or the Fourier transform of (12) of Connor & Taylor (Reference Connor and Taylor1987), or (B1) of Candy, Waltz & Rosenbluth (Reference Candy, Waltz and Rosenbluth2004)), neglect altogether the shear, i.e.
$R/L_{T}$
. Let us now consider the non-resonant limit. We take the fluid limit of the ITG equation (see (19) of Zocco et al. (Reference Zocco, Plunk, Xanthopoulos and Helander2016), or the Fourier transform of (12) of Connor & Taylor (Reference Connor and Taylor1987), or (B1) of Candy, Waltz & Rosenbluth (Reference Candy, Waltz and Rosenbluth2004)), neglect altogether the shear, i.e.
![]() ${\hat{s}}\equiv 0$
, and restore the streaming term, to obtain the Mathieu equation
${\hat{s}}\equiv 0$
, and restore the streaming term, to obtain the Mathieu equation
with
![]() $q(\unicode[STIX]{x1D714})=8\unicode[STIX]{x1D714}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}^{(0)}/(v_{\text{thi}}^{2}/\ell _{\Vert }^{2})$
,
$q(\unicode[STIX]{x1D714})=8\unicode[STIX]{x1D714}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}^{(0)}/(v_{\text{thi}}^{2}/\ell _{\Vert }^{2})$
,
![]() $a(\unicode[STIX]{x1D714})=-8(\unicode[STIX]{x1D714}^{3}/\unicode[STIX]{x1D714}_{T}v_{\text{thi}}^{2}/\ell _{\Vert }^{2})[\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D714}_{T}k_{y}^{2}\unicode[STIX]{x1D70C}_{i}^{2}/(2\unicode[STIX]{x1D714})]$
and
$a(\unicode[STIX]{x1D714})=-8(\unicode[STIX]{x1D714}^{3}/\unicode[STIX]{x1D714}_{T}v_{\text{thi}}^{2}/\ell _{\Vert }^{2})[\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D714}_{T}k_{y}^{2}\unicode[STIX]{x1D70C}_{i}^{2}/(2\unicode[STIX]{x1D714})]$
and
![]() $z=l/2$
, where
$z=l/2$
, where
![]() $l$
is the field-following coordinate and
$l$
is the field-following coordinate and
![]() $\ell _{\Vert }$
is the parallel connection length. Basically, when the system approaches marginality, the toroidal driving term (proportional to
$\ell _{\Vert }$
is the parallel connection length. Basically, when the system approaches marginality, the toroidal driving term (proportional to
![]() $q$
, not to be confused with the safety factor), becomes smaller and the second-order derivative associated with the streaming term cannot be neglected. The absence of secular terms due to very low shear, however, makes this non-resonant analysis still valid. The resonant theory of such modes does not seem straightforward.
$q$
, not to be confused with the safety factor), becomes smaller and the second-order derivative associated with the streaming term cannot be neglected. The absence of secular terms due to very low shear, however, makes this non-resonant analysis still valid. The resonant theory of such modes does not seem straightforward.

Figure 18. Spectra of instability for an
![]() ${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak,
${\hat{s}}-\unicode[STIX]{x1D6FC}$
tokamak,
![]() $\unicode[STIX]{x1D716}=0.1$
,
$\unicode[STIX]{x1D716}=0.1$
,
![]() $\unicode[STIX]{x1D70F}=1$
,
$\unicode[STIX]{x1D70F}=1$
,
![]() $R/L_{T}=3$
(background) and
$R/L_{T}=3$
(background) and
![]() $R/L_{T}=4$
(strong toroidal branch).
$R/L_{T}=4$
(strong toroidal branch).
Equation (4.1) has been studied in the context of formation of internal transport barriers in ITG turbulence by Candy et al. (Reference Candy, Waltz and Rosenbluth2004) and by Connor & Hastie (Reference Connor and Hastie2004). A more general form was investigated by Taylor & Wilson (Reference Taylor and Wilson1996). In stellarator research, ‘weakly localised’ Mathieu solutions were first identified by Bhattacharjee et al. (Reference Bhattacharjee, Sedlak, Similon, Rosenbluth and Ross1983).
The most general solution of (4.1) is
where
![]() $\unicode[STIX]{x1D6F7}$
is periodic with period
$\unicode[STIX]{x1D6F7}$
is periodic with period
![]() $\unicode[STIX]{x03C0}k$
, with
$\unicode[STIX]{x03C0}k$
, with
![]() $k$
integer. The evaluation of
$k$
integer. The evaluation of
![]() $\unicode[STIX]{x1D707}$
was first published in 1886 by Hill (Reference Hill1886), and it will now be applied to the ITG case. One introduces the Fourier series for the
$\unicode[STIX]{x1D707}$
was first published in 1886 by Hill (Reference Hill1886), and it will now be applied to the ITG case. One introduces the Fourier series for the
![]() $\unicode[STIX]{x03C0}$
-period solution
$\unicode[STIX]{x03C0}$
-period solution
to obtain
For a
![]() $2\unicode[STIX]{x03C0}$
-period solution,
$2\unicode[STIX]{x03C0}$
-period solution,
![]() $\unicode[STIX]{x1D711}_{2\unicode[STIX]{x03C0}}(z)=\text{e}^{\unicode[STIX]{x1D707}z}\sum _{n=-\infty }^{\infty }b_{2n}^{\prime }\exp [\text{i}nz]$
, we have
$\unicode[STIX]{x1D711}_{2\unicode[STIX]{x03C0}}(z)=\text{e}^{\unicode[STIX]{x1D707}z}\sum _{n=-\infty }^{\infty }b_{2n}^{\prime }\exp [\text{i}nz]$
, we have
where
![]() $c_{n}^{\prime }\equiv b_{2n}^{\prime }$
. Equation (4.5) is, for
$c_{n}^{\prime }\equiv b_{2n}^{\prime }$
. Equation (4.5) is, for
![]() $\unicode[STIX]{x1D707}=0$
, see (21) of Connor & Taylor (Reference Connor and Taylor1987). It is clear that
$\unicode[STIX]{x1D707}=0$
, see (21) of Connor & Taylor (Reference Connor and Taylor1987). It is clear that
![]() $\unicode[STIX]{x1D707}=0$
is the eigenvalue condition, because twisting boundary conditions require
$\unicode[STIX]{x1D707}=0$
is the eigenvalue condition, because twisting boundary conditions require
![]() $\unicode[STIX]{x1D711}^{\prime }(0)=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6F7}(0)+\unicode[STIX]{x1D6F7}^{\prime }(0)=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6F7}(0)=0$
, which, indeed, implies
$\unicode[STIX]{x1D711}^{\prime }(0)=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6F7}(0)+\unicode[STIX]{x1D6F7}^{\prime }(0)=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6F7}(0)=0$
, which, indeed, implies
![]() $\unicode[STIX]{x1D707}=0$
. Similarly, we introduce
$\unicode[STIX]{x1D707}=0$
. Similarly, we introduce
![]() $c_{n}\equiv b_{2n}$
and write (4.4) in matrix form,
$c_{n}\equiv b_{2n}$
and write (4.4) in matrix form,
![]() $\unicode[STIX]{x1D608}_{nm}c_{n}$
, where (for
$\unicode[STIX]{x1D608}_{nm}c_{n}$
, where (for
![]() $\unicode[STIX]{x03C0}$
-period solutions), after setting
$\unicode[STIX]{x03C0}$
-period solutions), after setting
![]() $\unicode[STIX]{x1D707}=0$
,
$\unicode[STIX]{x1D707}=0$
,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D608}_{mn}=\left(\begin{array}{@{}ccccc@{}}\ddots & \displaystyle -\frac{q}{a-4\times 2^{2}}\\ \displaystyle -\frac{q}{a-4\times 1^{2}} & 1 & \displaystyle -\frac{q}{a-4\times 1^{2}}\\ & \displaystyle -\frac{q}{a-4\times 0^{2}} & 1 & \displaystyle -\frac{q}{a-4\times 0^{2}}\\ & & \displaystyle -\frac{q}{a-4\times 1^{2}} & 1 & \displaystyle -\frac{q}{a-4\times 1^{2}}\\ & & & \displaystyle -\frac{q}{a-4\times 2^{2}} & \ddots \end{array}\right) & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D608}_{mn}=\left(\begin{array}{@{}ccccc@{}}\ddots & \displaystyle -\frac{q}{a-4\times 2^{2}}\\ \displaystyle -\frac{q}{a-4\times 1^{2}} & 1 & \displaystyle -\frac{q}{a-4\times 1^{2}}\\ & \displaystyle -\frac{q}{a-4\times 0^{2}} & 1 & \displaystyle -\frac{q}{a-4\times 0^{2}}\\ & & \displaystyle -\frac{q}{a-4\times 1^{2}} & 1 & \displaystyle -\frac{q}{a-4\times 1^{2}}\\ & & & \displaystyle -\frac{q}{a-4\times 2^{2}} & \ddots \end{array}\right) & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
is an infinite tridiagonal matrix. The eigenvalue,
![]() $\hat{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}/(v_{\text{thi}}/a)$
, is therefore determined from
$\hat{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}/(v_{\text{thi}}/a)$
, is therefore determined from
Notice that for
![]() $q\sim a$
, the off-diagonal elements decay like
$q\sim a$
, the off-diagonal elements decay like
![]() $m^{-2}$
, so the determinant of the matrix is convergent for
$m^{-2}$
, so the determinant of the matrix is convergent for
![]() $m\rightarrow \infty$
. For a given large
$m\rightarrow \infty$
. For a given large
![]() $M$
,
$M$
,
![]() $-M\leqslant (m,n)\leqslant M$
, one can use the iterative formula for determinants of tridiagonal matrices, to show that (4.7) can be written in terms of the truncated continued fraction
$-M\leqslant (m,n)\leqslant M$
, one can use the iterative formula for determinants of tridiagonal matrices, to show that (4.7) can be written in terms of the truncated continued fraction
 $$\begin{eqnarray}\displaystyle & & \displaystyle 1-\frac{q^{2}}{\left(a-4M^{2}\right)\left[a-4(M-1)^{2}\right]}\nonumber\\ \displaystyle & & \displaystyle \quad ~\times \frac{1}{\displaystyle 1-\frac{q^{2}}{\left[a-4(M-1)^{2}\right]\left[a-4(M-2)^{2}\right]}\frac{1}{\displaystyle 1-\frac{q^{2}}{\left[a-4(M-2)^{2}\right]\left[a-4(M-3)^{2}\right]}\frac{1}{1\ddots }}}\nonumber\\ \displaystyle & & \displaystyle \quad =0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 1-\frac{q^{2}}{\left(a-4M^{2}\right)\left[a-4(M-1)^{2}\right]}\nonumber\\ \displaystyle & & \displaystyle \quad ~\times \frac{1}{\displaystyle 1-\frac{q^{2}}{\left[a-4(M-1)^{2}\right]\left[a-4(M-2)^{2}\right]}\frac{1}{\displaystyle 1-\frac{q^{2}}{\left[a-4(M-2)^{2}\right]\left[a-4(M-3)^{2}\right]}\frac{1}{1\ddots }}}\nonumber\\ \displaystyle & & \displaystyle \quad =0,\end{eqnarray}$$
where the recursive formula is iterated from
![]() $m=M$
, to
$m=M$
, to
![]() $m=-M$
, with
$m=-M$
, with
![]() $\det A_{-M-1}\equiv 1$
. Then
$\det A_{-M-1}\equiv 1$
. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{M\rightarrow \infty }\frac{q^{2}}{\left(a-4M^{2}\right)\left[a-4(M-1)^{2}\right]}\nonumber\\ \displaystyle & & \displaystyle \quad ~\times \frac{1}{\displaystyle 1-\frac{q^{2}}{\left[a-4(M-1)^{2}\right]\left[a-4(M-2)^{2}\right]}\frac{1}{\displaystyle 1-\frac{q^{2}}{\left[a-4(M-2)^{2}\right]\left[a-4(M-3)^{2}\right]}\frac{1}{1-\ddots }}}\nonumber\\ \displaystyle & & \displaystyle \quad =1\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{M\rightarrow \infty }\frac{q^{2}}{\left(a-4M^{2}\right)\left[a-4(M-1)^{2}\right]}\nonumber\\ \displaystyle & & \displaystyle \quad ~\times \frac{1}{\displaystyle 1-\frac{q^{2}}{\left[a-4(M-1)^{2}\right]\left[a-4(M-2)^{2}\right]}\frac{1}{\displaystyle 1-\frac{q^{2}}{\left[a-4(M-2)^{2}\right]\left[a-4(M-3)^{2}\right]}\frac{1}{1-\ddots }}}\nonumber\\ \displaystyle & & \displaystyle \quad =1\end{eqnarray}$$
is the eigenvalue equation for the Floquet ITG mode. Candy et al. (Reference Candy, Waltz and Rosenbluth2004) report an eigenvalue condition which reads
and is valid only for
![]() $q\gg 1$
. Connor & Taylor (Reference Connor and Taylor1987) derived, for large
$q\gg 1$
. Connor & Taylor (Reference Connor and Taylor1987) derived, for large
![]() $q$
,
$q$
,
after expanding a finite
![]() ${\hat{s}}$
version of (4.1) in Fourier harmonics, and treating the Fourier index as a continuous variable. Following Connor and Taylor, we can consider slowly varying
${\hat{s}}$
version of (4.1) in Fourier harmonics, and treating the Fourier index as a continuous variable. Following Connor and Taylor, we can consider slowly varying
![]() $c_{m}$
coefficients, for the
$c_{m}$
coefficients, for the
![]() $\unicode[STIX]{x03C0}$
-period solution, and obtain
$\unicode[STIX]{x03C0}$
-period solution, and obtain
By using the ansatz
![]() $c_{m}=\exp [-\unicode[STIX]{x1D706}m^{2}]$
, the eigenvalue condition,
$c_{m}=\exp [-\unicode[STIX]{x1D706}m^{2}]$
, the eigenvalue condition,
is derived. This corresponds to equation (B9) of Candy et al. (Reference Candy, Waltz and Rosenbluth2004) for
![]() $q\rightarrow -q$
((4.10) in this work). In fact, both eigenvalue equations (4.5) and (4.13) are approximate forms of the exact one, for a different periodicity of
$q\rightarrow -q$
((4.10) in this work). In fact, both eigenvalue equations (4.5) and (4.13) are approximate forms of the exact one, for a different periodicity of
![]() $2\unicode[STIX]{x03C0}$
or
$2\unicode[STIX]{x03C0}$
or
![]() $\unicode[STIX]{x03C0}$
, respectively. For each periodicity, we have two eigenmodes (and eigenvalues) depending on the argument of
$\unicode[STIX]{x03C0}$
, respectively. For each periodicity, we have two eigenmodes (and eigenvalues) depending on the argument of
![]() $q$
. For instance, the
$q$
. For instance, the
![]() $2\unicode[STIX]{x03C0}$
-period solutions have maxima at the poloidal location
$2\unicode[STIX]{x03C0}$
-period solutions have maxima at the poloidal location
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
, equation (4.11) and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
, equation (4.11) and
![]() $\unicode[STIX]{x1D703}=0$
((4.11) with
$\unicode[STIX]{x1D703}=0$
((4.11) with
![]() $q\rightarrow -q$
).
$q\rightarrow -q$
).
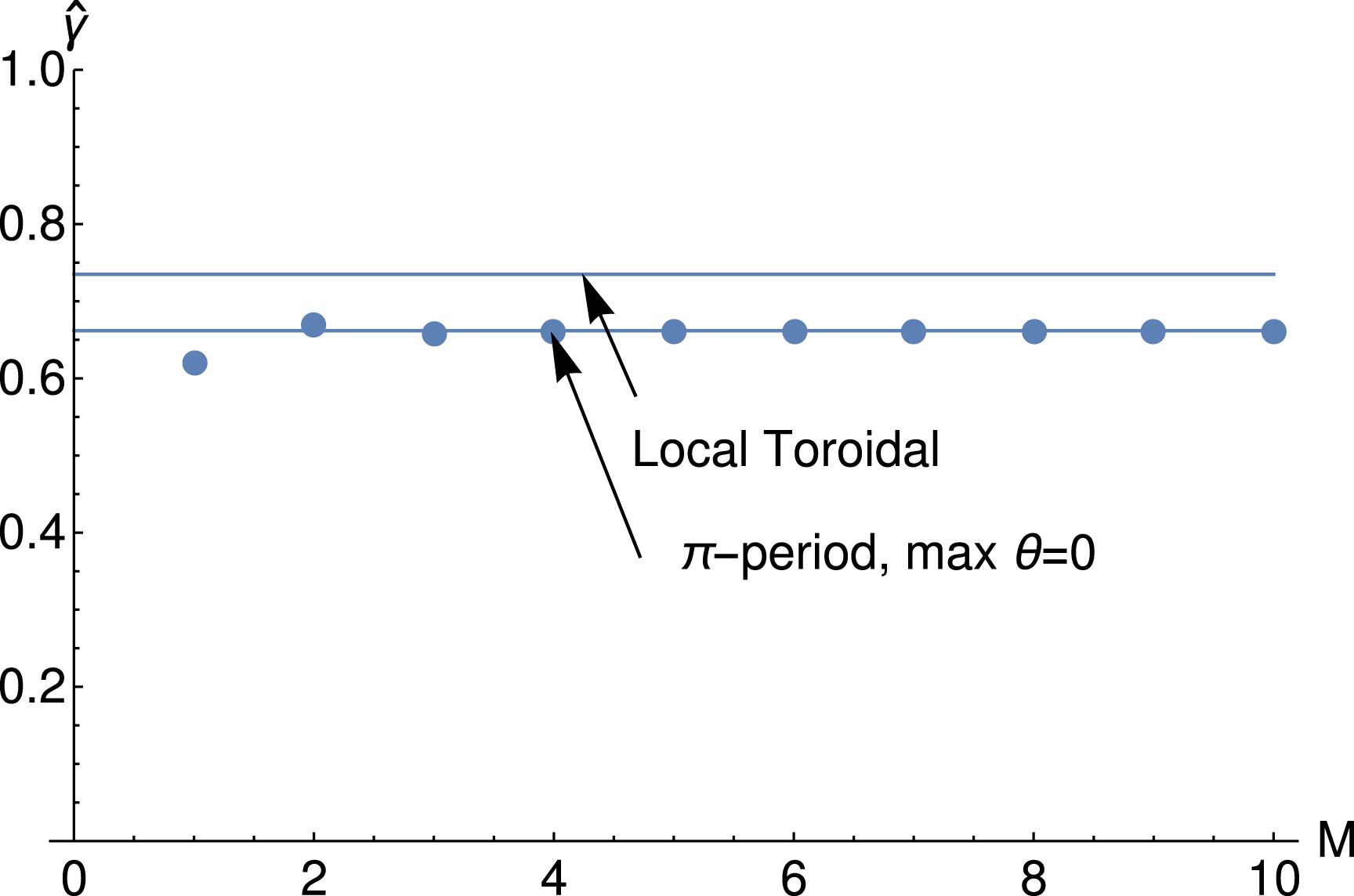
The numerical solution of (4.7),
![]() $\hat{\unicode[STIX]{x1D6FE}}=\text{Im}[\hat{\unicode[STIX]{x1D714}}]$
, is plotted in figure 19 as a function of the matrix dimension for
$\hat{\unicode[STIX]{x1D6FE}}=\text{Im}[\hat{\unicode[STIX]{x1D714}}]$
, is plotted in figure 19 as a function of the matrix dimension for
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}^{(0)}/(v_{\text{thi}}/a)=0.45$
,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}^{(0)}/(v_{\text{thi}}/a)=0.45$
,
![]() $\unicode[STIX]{x1D714}_{T}/(v_{\text{thi}}/a)=0.6$
,
$\unicode[STIX]{x1D714}_{T}/(v_{\text{thi}}/a)=0.6$
,
![]() $v_{\text{thi}}/\ell _{\Vert }=0.5(v_{\text{thi}}/a)$
and
$v_{\text{thi}}/\ell _{\Vert }=0.5(v_{\text{thi}}/a)$
and
![]() $k_{y}\unicode[STIX]{x1D70C}_{i}=0.3$
(here
$k_{y}\unicode[STIX]{x1D70C}_{i}=0.3$
(here
![]() $a$
is a normalising length). The result is compared to the solution of (4.13). In this case
$a$
is a normalising length). The result is compared to the solution of (4.13). In this case
![]() $q=10$
. The agreement is excellent. For
$q=10$
. The agreement is excellent. For
![]() $q\sim 1$
, which is the relevant regime, since (4.1) is derived for
$q\sim 1$
, which is the relevant regime, since (4.1) is derived for
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}/\unicode[STIX]{x1D714}\sim v_{\text{thi}}^{2}/\ell _{\Vert }^{2}\ll 1$
, equation (4.7) is the correct eigenvalue equation. It is worth mentioning that Taylor & Hastie (Reference Taylor and Hastie1968), in their seminal work where linear gyrokinetics was derived for the first time for electrostatic perturbations in a torus, report an eigenvalue equation of the form of our (4.7). Their eigenvalue equation (50) reduces to a determinant of a tridiagonal matrix (derived by Coppi et al.
Reference Coppi, Laval, Pellat and Rosenbluth1968), when the plane slab ITG is modified by a sinusoidal periodic gravity term. Coppi et al. recognised the role of the Hill determinant in the evaluation of the true eigenvalue given by the solution of (4.7), but the approximated eigenvalue of (4.11) was derived only
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}/\unicode[STIX]{x1D714}\sim v_{\text{thi}}^{2}/\ell _{\Vert }^{2}\ll 1$
, equation (4.7) is the correct eigenvalue equation. It is worth mentioning that Taylor & Hastie (Reference Taylor and Hastie1968), in their seminal work where linear gyrokinetics was derived for the first time for electrostatic perturbations in a torus, report an eigenvalue equation of the form of our (4.7). Their eigenvalue equation (50) reduces to a determinant of a tridiagonal matrix (derived by Coppi et al.
Reference Coppi, Laval, Pellat and Rosenbluth1968), when the plane slab ITG is modified by a sinusoidal periodic gravity term. Coppi et al. recognised the role of the Hill determinant in the evaluation of the true eigenvalue given by the solution of (4.7), but the approximated eigenvalue of (4.11) was derived only
![]() $19$
years later! We now see that the resonant destabilisation of Floquet modes in stellarators can possibly be compared with the final result derived by Coppi et al. (Reference Coppi, Laval, Pellat and Rosenbluth1968) in appendix B of their work, if temperature-gradient effects are included.
$19$
years later! We now see that the resonant destabilisation of Floquet modes in stellarators can possibly be compared with the final result derived by Coppi et al. (Reference Coppi, Laval, Pellat and Rosenbluth1968) in appendix B of their work, if temperature-gradient effects are included.
5 Discussion and conclusions
The aim of this work was to elucidate what sets the linear threshold for destabilisation of the electrostatic ion-temperature-gradient driven mode in toroidal magnetic fusion devices. We study both axisymmetric (tokamaks) and non-axisymmetric (stellartors) confinement concepts.
In regimes of interest for the stellarator Wendelstein 7-X, a background of unstable modes exists below the threshold of destabilisation of the toroidal branch of the ITG mode. We proposed the hypothesis that such modes are ITG modes of the Floquet type. The eigenfunctions resulting from GENE numerical simulations of Wendelstein 7-X show a much slower decay along the field line for these modes than for modes of the toroidal branch (see figure 14). This behaviour is evocative of the prediction of weakly localised drift-wave modes in stellarators, described in terms of Mathieu functions by Bhattacharjee et al. (Reference Bhattacharjee, Sedlak, Similon, Rosenbluth and Ross1983). In the non-resonant limit, a complete eigenvalue equation is then proposed and studied in relation to previously known results.
The importance of our findings relies on the fact that such modes result from having a very low global shear,
![]() ${\hat{s}}$
, and feature similar qualitative behaviour in tokamaks and stellarators. In the former case, one could imagine them being relevant for advanced confinement scenarios with very flat safety factor profiles. For finite density gradients, the insensitivity of the derived temperature gradient thresholds to the temperature ratio
${\hat{s}}$
, and feature similar qualitative behaviour in tokamaks and stellarators. In the former case, one could imagine them being relevant for advanced confinement scenarios with very flat safety factor profiles. For finite density gradients, the insensitivity of the derived temperature gradient thresholds to the temperature ratio
![]() $\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
for
$\unicode[STIX]{x1D70F}=T_{i}/T_{e}$
for
![]() $\unicode[STIX]{x1D70F}<1$
seems a rather clear effect, distinguishing these modes from the more conventional branches. For stellarators, our findings could have a non-negligible impact on confinement if Floquet solutions play any role nonlinearly. If stellarator electrostatic turbulence is affected by the nonlinear activity of these modes, there is an open question regarding what is really the achievable temperature gradient for a stellarator with low global shear, as opposed to known tokamak cases, where a finite turbulent transport is observed above a finite critical temperature gradient, generally larger than the one discussed in this work (Dimits et al.
Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000). Additional stabilising effects can of course suppress these modes. Our results are perhaps also relevant for trapped-electron mode driven turbulence, where similar eigenfunctions and ‘background’ modes can be observed (Proll, Xanthopoulos & Helander Reference Proll, Xanthopoulos and Helander2013; Faber et al.
Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015).
$\unicode[STIX]{x1D70F}<1$
seems a rather clear effect, distinguishing these modes from the more conventional branches. For stellarators, our findings could have a non-negligible impact on confinement if Floquet solutions play any role nonlinearly. If stellarator electrostatic turbulence is affected by the nonlinear activity of these modes, there is an open question regarding what is really the achievable temperature gradient for a stellarator with low global shear, as opposed to known tokamak cases, where a finite turbulent transport is observed above a finite critical temperature gradient, generally larger than the one discussed in this work (Dimits et al.
Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000). Additional stabilising effects can of course suppress these modes. Our results are perhaps also relevant for trapped-electron mode driven turbulence, where similar eigenfunctions and ‘background’ modes can be observed (Proll, Xanthopoulos & Helander Reference Proll, Xanthopoulos and Helander2013; Faber et al.
Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015).
Acknowledgements
Part of this work was presented at the first conference ‘Frontiers in Plasma Physics’, held at the Abbey of the Most Holy Trinity of Spineto (Sarteano, Italy) under the auspices of the Journal of Plasma Physics (Cambridge University Press).
Appendix A. Local kinetic limit formulation
In order to solve the integral
![]() $I_{i}$
for arbitrary ion Larmor radii, some preliminary manipulations are in order. We add and subtract
$I_{i}$
for arbitrary ion Larmor radii, some preliminary manipulations are in order. We add and subtract
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}\hat{v}_{\Vert }^{2}+\unicode[STIX]{x1D714}_{B}\hat{v}_{\bot }^{2}/2$
in the numerator of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}\hat{v}_{\Vert }^{2}+\unicode[STIX]{x1D714}_{B}\hat{v}_{\bot }^{2}/2$
in the numerator of
![]() $I_{i}$
to obtain
$I_{i}$
to obtain
 $$\begin{eqnarray}\displaystyle I_{i} & = & \displaystyle 2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }J_{0}^{2}\left(\boldsymbol{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}\hat{v}_{\bot }^{2}\right)\text{e}^{-\hat{v}_{\bot }^{2}}-\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\left(1-\frac{3}{2}\unicode[STIX]{x1D702}_{i}\right)J^{(0)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}-\unicode[STIX]{x1D714}_{\ast i}\unicode[STIX]{x1D702}_{i}}{\unicode[STIX]{x1D714}}J_{\bot }^{(2)}+\frac{\unicode[STIX]{x1D714}_{B}/2-\unicode[STIX]{x1D714}_{\ast i}\unicode[STIX]{x1D702}_{i}}{\unicode[STIX]{x1D714}}J_{\Vert }^{(2)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{i} & = & \displaystyle 2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }J_{0}^{2}\left(\boldsymbol{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}\hat{v}_{\bot }^{2}\right)\text{e}^{-\hat{v}_{\bot }^{2}}-\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\left(1-\frac{3}{2}\unicode[STIX]{x1D702}_{i}\right)J^{(0)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}-\unicode[STIX]{x1D714}_{\ast i}\unicode[STIX]{x1D702}_{i}}{\unicode[STIX]{x1D714}}J_{\bot }^{(2)}+\frac{\unicode[STIX]{x1D714}_{B}/2-\unicode[STIX]{x1D714}_{\ast i}\unicode[STIX]{x1D702}_{i}}{\unicode[STIX]{x1D714}}J_{\Vert }^{(2)},\end{eqnarray}$$
with
 $$\begin{eqnarray}J_{\bot ,\Vert }^{(n)}=2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }\int _{-\infty }^{\infty }\text{d}\hat{v}_{\Vert }\hat{v}_{\bot ,\Vert }^{n}\frac{J_{0}^{2}\left(\boldsymbol{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}\hat{v}_{\bot }^{2}\right)}{1-\left(\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\hat{v}_{\Vert }^{2}+\frac{\unicode[STIX]{x1D714}_{B}}{\unicode[STIX]{x1D714}}\hat{v}_{\bot }^{2}/2\right)}\frac{\text{e}^{-(\hat{v}_{\Vert }^{2}+\hat{v}_{\bot }^{2})}}{\sqrt{\unicode[STIX]{x03C0}}}.\end{eqnarray}$$
$$\begin{eqnarray}J_{\bot ,\Vert }^{(n)}=2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }\int _{-\infty }^{\infty }\text{d}\hat{v}_{\Vert }\hat{v}_{\bot ,\Vert }^{n}\frac{J_{0}^{2}\left(\boldsymbol{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}\hat{v}_{\bot }^{2}\right)}{1-\left(\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\hat{v}_{\Vert }^{2}+\frac{\unicode[STIX]{x1D714}_{B}}{\unicode[STIX]{x1D714}}\hat{v}_{\bot }^{2}/2\right)}\frac{\text{e}^{-(\hat{v}_{\Vert }^{2}+\hat{v}_{\bot }^{2})}}{\sqrt{\unicode[STIX]{x03C0}}}.\end{eqnarray}$$
The first line of (A 1) gives the well-known result of gyrokinetic theory:
where
![]() $b=\boldsymbol{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}/2$
, and
$b=\boldsymbol{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}/2$
, and
![]() $\unicode[STIX]{x1D6E4}_{0}(b)=\text{I}_{0}(b)\exp (-b)$
, with
$\unicode[STIX]{x1D6E4}_{0}(b)=\text{I}_{0}(b)\exp (-b)$
, with
![]() $\text{I}_{0}$
the modified Bessel function. We now integrate the resonances in a way similar to that presented by Biglari, Diamond and Rosenbluth (BDR) (Biglari et al.
Reference Biglari, Diamond and Rosenbluth1989). For
$\text{I}_{0}$
the modified Bessel function. We now integrate the resonances in a way similar to that presented by Biglari, Diamond and Rosenbluth (BDR) (Biglari et al.
Reference Biglari, Diamond and Rosenbluth1989). For
![]() $J^{(0)}$
we have
$J^{(0)}$
we have
 $$\begin{eqnarray}\displaystyle J^{(0)} & = & \displaystyle \displaystyle -2\text{i}\int _{0}^{\infty }\!\!\text{d}\hat{v}_{\bot }\hat{v}_{\bot }J_{0}^{2}\int _{-\infty }^{\infty }\!\!\frac{\text{d}\hat{v}_{\Vert }}{\sqrt{\unicode[STIX]{x03C0}}}\int _{0}^{\infty }\!\!\text{d}\unicode[STIX]{x1D706}\exp \left(\text{i}\unicode[STIX]{x1D706}\left[1-\!\!\left.\left(\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\hat{v}_{\Vert }^{2}+\frac{\unicode[STIX]{x1D714}_{B}}{\unicode[STIX]{x1D714}}\hat{v}_{\bot }^{2}\right/2\!\right)\right]\!-(\hat{v}_{\Vert }^{2}+\hat{v}_{\bot }^{2})\!\right)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle -2\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\,\text{e}^{\text{i}\unicode[STIX]{x1D706}}\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }J_{0}^{2}\int _{-\infty }^{\infty }\frac{\text{d}\hat{v}_{\Vert }}{\sqrt{\unicode[STIX]{x03C0}}}\text{e}^{-\hat{v}_{\bot }^{2}\left(1+\text{i}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D714}_{B}/2\unicode[STIX]{x1D714})\right)}\text{e}^{-\hat{v}_{\Vert }^{2}\left(1+\text{i}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}/\unicode[STIX]{x1D714})\right)}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle -2\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\,\text{e}^{\text{i}\unicode[STIX]{x1D706}}\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }J_{0}^{2}\frac{\text{e}^{-\hat{v}_{\bot }^{2}\left(1+\text{i}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D714}_{B}/2\unicode[STIX]{x1D714})\right)}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{1/2}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle -\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{1/2}}\frac{\unicode[STIX]{x1D6E4}_{0}(\hat{b})}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J^{(0)} & = & \displaystyle \displaystyle -2\text{i}\int _{0}^{\infty }\!\!\text{d}\hat{v}_{\bot }\hat{v}_{\bot }J_{0}^{2}\int _{-\infty }^{\infty }\!\!\frac{\text{d}\hat{v}_{\Vert }}{\sqrt{\unicode[STIX]{x03C0}}}\int _{0}^{\infty }\!\!\text{d}\unicode[STIX]{x1D706}\exp \left(\text{i}\unicode[STIX]{x1D706}\left[1-\!\!\left.\left(\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\hat{v}_{\Vert }^{2}+\frac{\unicode[STIX]{x1D714}_{B}}{\unicode[STIX]{x1D714}}\hat{v}_{\bot }^{2}\right/2\!\right)\right]\!-(\hat{v}_{\Vert }^{2}+\hat{v}_{\bot }^{2})\!\right)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle -2\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\,\text{e}^{\text{i}\unicode[STIX]{x1D706}}\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }J_{0}^{2}\int _{-\infty }^{\infty }\frac{\text{d}\hat{v}_{\Vert }}{\sqrt{\unicode[STIX]{x03C0}}}\text{e}^{-\hat{v}_{\bot }^{2}\left(1+\text{i}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D714}_{B}/2\unicode[STIX]{x1D714})\right)}\text{e}^{-\hat{v}_{\Vert }^{2}\left(1+\text{i}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}/\unicode[STIX]{x1D714})\right)}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle -2\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\,\text{e}^{\text{i}\unicode[STIX]{x1D706}}\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }J_{0}^{2}\frac{\text{e}^{-\hat{v}_{\bot }^{2}\left(1+\text{i}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D714}_{B}/2\unicode[STIX]{x1D714})\right)}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{1/2}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle -\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{1/2}}\frac{\unicode[STIX]{x1D6E4}_{0}(\hat{b})}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}},\end{eqnarray}$$
with
![]() $\hat{b}=b/[1+\text{i}\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{B}/(2\unicode[STIX]{x1D714})]$
. We require
$\hat{b}=b/[1+\text{i}\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}_{B}/(2\unicode[STIX]{x1D714})]$
. We require
and
in order to guarantee convergence of the velocity space and
![]() $\unicode[STIX]{x1D706}$
integrals, respectively. Conditions (A 5)–(A 7) thus define an abscissa of convergence in the complex
$\unicode[STIX]{x1D706}$
integrals, respectively. Conditions (A 5)–(A 7) thus define an abscissa of convergence in the complex
![]() $\unicode[STIX]{x1D706}$
-plane
$\unicode[STIX]{x1D706}$
-plane
Here we are using
![]() $\unicode[STIX]{x1D714}_{B}\equiv \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
(valid in the low-
$\unicode[STIX]{x1D714}_{B}\equiv \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
(valid in the low-
![]() $\unicode[STIX]{x1D6FD}$
case, where
$\unicode[STIX]{x1D6FD}$
case, where
![]() $\unicode[STIX]{x1D6FD}$
is the ratio of kinetic and magnetic plasma pressure) and taking the most restrictive of conditions (A 5)–(A 7). Similarly, we obtain
$\unicode[STIX]{x1D6FD}$
is the ratio of kinetic and magnetic plasma pressure) and taking the most restrictive of conditions (A 5)–(A 7). Similarly, we obtain
 $$\begin{eqnarray}J_{\Vert }^{(2)}=-\frac{\text{i}}{2}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{3/2}}\frac{\unicode[STIX]{x1D6E4}_{0}(\hat{b})}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}},\end{eqnarray}$$
$$\begin{eqnarray}J_{\Vert }^{(2)}=-\frac{\text{i}}{2}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{3/2}}\frac{\unicode[STIX]{x1D6E4}_{0}(\hat{b})}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}},\end{eqnarray}$$
and
 $$\begin{eqnarray}J_{\bot }^{(2)}=-\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{1/2}}\frac{\unicode[STIX]{x1D6E4}_{0}(\hat{b})+\hat{b}\left[\unicode[STIX]{x1D6E4}_{1}(\hat{b})-\unicode[STIX]{x1D6E4}_{0}(\hat{b})\right]}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}\right)^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}J_{\bot }^{(2)}=-\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{1/2}}\frac{\unicode[STIX]{x1D6E4}_{0}(\hat{b})+\hat{b}\left[\unicode[STIX]{x1D6E4}_{1}(\hat{b})-\unicode[STIX]{x1D6E4}_{0}(\hat{b})\right]}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}\right)^{2}}.\end{eqnarray}$$
We now introduce the Padé approximants
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{0}(\hat{b})\approx \frac{1}{1+\displaystyle \frac{b}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{0}(\hat{b})\approx \frac{1}{1+\displaystyle \frac{b}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}}},\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{0}(\hat{b})+\hat{b}\left[\unicode[STIX]{x1D6E4}_{1}(\hat{b})-\unicode[STIX]{x1D6E4}_{0}(\hat{b})\right]\approx \frac{1}{\left(1+\displaystyle \frac{b}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}}\right)^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{0}(\hat{b})+\hat{b}\left[\unicode[STIX]{x1D6E4}_{1}(\hat{b})-\unicode[STIX]{x1D6E4}_{0}(\hat{b})\right]\approx \frac{1}{\left(1+\displaystyle \frac{b}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}}\right)^{2}},\end{eqnarray}$$
which will allow us to perform the
![]() $\unicode[STIX]{x1D706}$
integration. The integral
$\unicode[STIX]{x1D706}$
integration. The integral
![]() $J^{(0)}$
becomes
$J^{(0)}$
becomes
 $$\begin{eqnarray}\displaystyle & \displaystyle J^{(0)}=-\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{1/2}}\displaystyle \frac{1}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}+b}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J^{(0)}=-\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{1/2}}\displaystyle \frac{1}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}+b}. & \displaystyle\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
,
$\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
,
![]() $b\rightarrow 0$
, and
$b\rightarrow 0$
, and
![]() $\unicode[STIX]{x1D714}_{B}\equiv \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
,
$\unicode[STIX]{x1D714}_{B}\equiv \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
,
 $$\begin{eqnarray}\displaystyle \lim _{b\rightarrow 0}J^{(0)} & = & \displaystyle \displaystyle -\text{i}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\right)^{1/2}}\frac{1}{1+\text{i}\displaystyle \frac{\unicode[STIX]{x1D706}}{2}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}F_{1,1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{b\rightarrow 0}J^{(0)} & = & \displaystyle \displaystyle -\text{i}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\right)^{1/2}}\frac{1}{1+\text{i}\displaystyle \frac{\unicode[STIX]{x1D706}}{2}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}F_{1,1},\end{eqnarray}$$
with
![]() $F_{1,1}$
defined in (A2) of BDR. We notice that the change of variables
$F_{1,1}$
defined in (A2) of BDR. We notice that the change of variables
![]() $\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
requires
$\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
requires
![]() $(\text{Re}[\unicode[STIX]{x1D706}]\text{Im}[\unicode[STIX]{x1D714}]+\text{Im}[\unicode[STIX]{x1D706}]\text{Re}[\unicode[STIX]{x1D714}])/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}>0$
for the convergence of the
$(\text{Re}[\unicode[STIX]{x1D706}]\text{Im}[\unicode[STIX]{x1D714}]+\text{Im}[\unicode[STIX]{x1D706}]\text{Re}[\unicode[STIX]{x1D714}])/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}>0$
for the convergence of the
![]() $\unicode[STIX]{x1D706}$
integral. At marginal stability, for
$\unicode[STIX]{x1D706}$
integral. At marginal stability, for
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}<0$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}<0$
and
![]() $\unicode[STIX]{x1D714}<0$
, this is condition (A 7).
$\unicode[STIX]{x1D714}<0$
, this is condition (A 7).
Appendix B. Arbitrary Larmor radii solution
For
![]() $b\neq 0$
, the analytical technique used by BDR to solve for
$b\neq 0$
, the analytical technique used by BDR to solve for
![]() $F_{1,1}$
cannot be used to perform the integration. We prefer to proceed in a different way.
$F_{1,1}$
cannot be used to perform the integration. We prefer to proceed in a different way.
Let us consider
 $$\begin{eqnarray}R=-\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\right)^{1/2}}\frac{1}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}+b},\end{eqnarray}$$
$$\begin{eqnarray}R=-\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\right)^{1/2}}\frac{1}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}+b},\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
. We change variables
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
. We change variables
and obtain
 $$\begin{eqnarray}\displaystyle R & = & \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\int _{1}^{\text{e}^{\text{i}(\unicode[STIX]{x03C0}/4)}\infty }\text{d}t\frac{\text{e}^{\unicode[STIX]{x1D6FA}(t^{2}-1)}}{2\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}(1+b)-1+t^{2}}\nonumber\\ \displaystyle & = & \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\text{e}^{-\unicode[STIX]{x1D6FA}}\int _{1/\sqrt{g}}^{\text{e}^{\text{i}(\unicode[STIX]{x03C0}/4)}\infty }\frac{\text{d}u}{\sqrt{g}}\frac{\text{e}^{\unicode[STIX]{x1D6FA}gu^{2}}}{1+u^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R & = & \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\int _{1}^{\text{e}^{\text{i}(\unicode[STIX]{x03C0}/4)}\infty }\text{d}t\frac{\text{e}^{\unicode[STIX]{x1D6FA}(t^{2}-1)}}{2\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}(1+b)-1+t^{2}}\nonumber\\ \displaystyle & = & \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\text{e}^{-\unicode[STIX]{x1D6FA}}\int _{1/\sqrt{g}}^{\text{e}^{\text{i}(\unicode[STIX]{x03C0}/4)}\infty }\frac{\text{d}u}{\sqrt{g}}\frac{\text{e}^{\unicode[STIX]{x1D6FA}gu^{2}}}{1+u^{2}},\end{eqnarray}$$
with
In the case
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}=\unicode[STIX]{x1D714}_{B}$
,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}=\unicode[STIX]{x1D714}_{B}$
,
![]() $g=1+2b>0\,\forall \,b$
. We split the domain of integration and define
$g=1+2b>0\,\forall \,b$
. We split the domain of integration and define
 $$\begin{eqnarray}\displaystyle R & = & \displaystyle \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\text{e}^{-\unicode[STIX]{x1D6FA}}\left(\int _{0}^{\text{e}^{\text{i}(\unicode[STIX]{x03C0}/4)}\infty }\frac{\text{d}u}{\sqrt{g}}-\int _{0}^{1/\sqrt{g}}\frac{\text{d}u}{\sqrt{g}}\right)\frac{\text{e}^{\unicode[STIX]{x1D6FA}gu^{2}}}{1+u^{2}}\nonumber\\ \displaystyle & \equiv & \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\text{e}^{-\unicode[STIX]{x1D6FA}}\left(I_{\infty }-I_{g}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R & = & \displaystyle \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\text{e}^{-\unicode[STIX]{x1D6FA}}\left(\int _{0}^{\text{e}^{\text{i}(\unicode[STIX]{x03C0}/4)}\infty }\frac{\text{d}u}{\sqrt{g}}-\int _{0}^{1/\sqrt{g}}\frac{\text{d}u}{\sqrt{g}}\right)\frac{\text{e}^{\unicode[STIX]{x1D6FA}gu^{2}}}{1+u^{2}}\nonumber\\ \displaystyle & \equiv & \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\text{e}^{-\unicode[STIX]{x1D6FA}}\left(I_{\infty }-I_{g}\right).\end{eqnarray}$$
In appendices C and D, we show that
where
![]() $Z$
is the plasma dispersion function (Fried & Conte Reference Fried and Conte1961), and
$Z$
is the plasma dispersion function (Fried & Conte Reference Fried and Conte1961), and
![]() $T$
the Owen
$T$
the Owen
![]() $T$
-function (Owen Reference Owen1956). By direct comparison of (A 13) and (B 1), we have
$T$
-function (Owen Reference Owen1956). By direct comparison of (A 13) and (B 1), we have
The integral
![]() $J_{\bot }^{(2)}$
now becomes
$J_{\bot }^{(2)}$
now becomes
 $$\begin{eqnarray}\displaystyle J_{\bot }^{(2)} & = & \displaystyle -\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{1/2}}\frac{1}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}+b\right)^{2}}\nonumber\\ \displaystyle & = & \displaystyle -\frac{\text{d}}{\text{d}b}J^{(0)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{\bot }^{(2)} & = & \displaystyle -\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D706}}}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}}\right)^{1/2}}\frac{1}{\left(1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}}+b\right)^{2}}\nonumber\\ \displaystyle & = & \displaystyle -\frac{\text{d}}{\text{d}b}J^{(0)}.\end{eqnarray}$$
To evaluate the integral
![]() $J_{\Vert }^{(2)}$
, it is convenient to consider a simple generalisation of the auxiliary integral,
$J_{\Vert }^{(2)}$
, it is convenient to consider a simple generalisation of the auxiliary integral,
![]() $R$
, namely
$R$
, namely
 $$\begin{eqnarray}R_{\unicode[STIX]{x1D708}}=-\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D706}}}{\left(\unicode[STIX]{x1D708}+\text{i}\unicode[STIX]{x1D706}\right)^{1/2}}\frac{1}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}+b}.\end{eqnarray}$$
$$\begin{eqnarray}R_{\unicode[STIX]{x1D708}}=-\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D706}\frac{\text{e}^{\text{i}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D706}}}{\left(\unicode[STIX]{x1D708}+\text{i}\unicode[STIX]{x1D706}\right)^{1/2}}\frac{1}{1+\text{i}\unicode[STIX]{x1D706}\displaystyle \frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}+b}.\end{eqnarray}$$
Then
The integral
![]() $R_{\unicode[STIX]{x1D708}}$
can be related to
$R_{\unicode[STIX]{x1D708}}$
can be related to
![]() $R$
after some straightforward algebra. We find
$R$
after some straightforward algebra. We find
 $$\begin{eqnarray}\displaystyle R_{\unicode[STIX]{x1D708}} & = & \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\text{e}^{-\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FA}}\int _{\sqrt{\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}}}}^{\text{e}^{\text{i}(\unicode[STIX]{x03C0}/4)\infty }}\frac{\text{d}u}{\sqrt{g_{\unicode[STIX]{x1D708}}}}\frac{\text{e}^{g_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6FA}u^{2}}}{1+u^{2}}\nonumber\\ \displaystyle & = & \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\frac{\text{e}^{-\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FA}}}{\sqrt{g_{\unicode[STIX]{x1D708}}}}\left\{-\frac{\text{i}}{2}\sqrt{\unicode[STIX]{x03C0}}Z(\sqrt{g_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6FA}})-2\unicode[STIX]{x03C0}\text{e}^{-g_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6FA}}T\left[\text{i}\sqrt{2g_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6FA}};\sqrt{\frac{\unicode[STIX]{x1D708}}{g_{\unicode[STIX]{x1D708}}}}\right]\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{\unicode[STIX]{x1D708}} & = & \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\text{e}^{-\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FA}}\int _{\sqrt{\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}}}}^{\text{e}^{\text{i}(\unicode[STIX]{x03C0}/4)\infty }}\frac{\text{d}u}{\sqrt{g_{\unicode[STIX]{x1D708}}}}\frac{\text{e}^{g_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6FA}u^{2}}}{1+u^{2}}\nonumber\\ \displaystyle & = & \displaystyle -4\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{B}}\frac{\text{e}^{-\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FA}}}{\sqrt{g_{\unicode[STIX]{x1D708}}}}\left\{-\frac{\text{i}}{2}\sqrt{\unicode[STIX]{x03C0}}Z(\sqrt{g_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6FA}})-2\unicode[STIX]{x03C0}\text{e}^{-g_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6FA}}T\left[\text{i}\sqrt{2g_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6FA}};\sqrt{\frac{\unicode[STIX]{x1D708}}{g_{\unicode[STIX]{x1D708}}}}\right]\right\},\end{eqnarray}$$
with
Summarising, the local kinetic dispersion relation is
 $$\begin{eqnarray}\displaystyle 1+\unicode[STIX]{x1D70F} & = & \displaystyle \unicode[STIX]{x1D6E4}_{0}(b)-\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\left(1-\frac{3}{2}\unicode[STIX]{x1D702}_{i}\right)J_{\bot }^{(0)}\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\left(\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{\ast i}}-\unicode[STIX]{x1D702}_{i}\right)J_{\bot }^{(2)}+\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\left(\frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}_{\ast i}}-\unicode[STIX]{x1D702}_{i}\right)J_{\Vert }^{(2)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1+\unicode[STIX]{x1D70F} & = & \displaystyle \unicode[STIX]{x1D6E4}_{0}(b)-\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\left(1-\frac{3}{2}\unicode[STIX]{x1D702}_{i}\right)J_{\bot }^{(0)}\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\left(\frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}{\unicode[STIX]{x1D714}_{\ast i}}-\unicode[STIX]{x1D702}_{i}\right)J_{\bot }^{(2)}+\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\left(\frac{\unicode[STIX]{x1D714}_{B}}{2\unicode[STIX]{x1D714}_{\ast i}}-\unicode[STIX]{x1D702}_{i}\right)J_{\Vert }^{(2)},\end{eqnarray}$$
with
with
![]() $R_{\unicode[STIX]{x1D708}}$
defined in (B 11),
$R_{\unicode[STIX]{x1D708}}$
defined in (B 11),
![]() $g_{\unicode[STIX]{x1D708}}=2(1+b)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}/\unicode[STIX]{x1D714}_{B}-\unicode[STIX]{x1D708}$
, and
$g_{\unicode[STIX]{x1D708}}=2(1+b)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}/\unicode[STIX]{x1D714}_{B}-\unicode[STIX]{x1D708}$
, and
 $$\begin{eqnarray}T\left[\text{i}\sqrt{2g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}};\sqrt{\frac{\unicode[STIX]{x1D708}}{g_{\unicode[STIX]{x1D708}}}}\right]=\frac{\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\mathop{\sum }_{n=0}^{\infty }\displaystyle \frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{(2n+1)}\mathop{\sum }_{m=0}^{n}\frac{\displaystyle \left(-g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)^{m}}{m!}.\end{eqnarray}$$
$$\begin{eqnarray}T\left[\text{i}\sqrt{2g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}};\sqrt{\frac{\unicode[STIX]{x1D708}}{g_{\unicode[STIX]{x1D708}}}}\right]=\frac{\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\mathop{\sum }_{n=0}^{\infty }\displaystyle \frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{(2n+1)}\mathop{\sum }_{m=0}^{n}\frac{\displaystyle \left(-g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)^{m}}{m!}.\end{eqnarray}$$
This expression for the Owen
![]() $T$
-function is derived in appendix D.
$T$
-function is derived in appendix D.
Appendix C. The integral
 $I_{\infty }$
$I_{\infty }$
For
![]() $I_{\infty }$
, we change variables to
$I_{\infty }$
, we change variables to
so that, when
![]() $u\rightarrow \text{e}^{\text{i}(\unicode[STIX]{x03C0}/4)}\infty$
,
$u\rightarrow \text{e}^{\text{i}(\unicode[STIX]{x03C0}/4)}\infty$
,
![]() $\unicode[STIX]{x1D709}\rightarrow \text{e}^{\text{i}\left((3/4)\unicode[STIX]{x03C0}+(\text{argg}\unicode[STIX]{x1D6FA})/2\right)}\infty$
. A closed form of the integral can be found for an unstable mode
$\unicode[STIX]{x1D709}\rightarrow \text{e}^{\text{i}\left((3/4)\unicode[STIX]{x03C0}+(\text{argg}\unicode[STIX]{x1D6FA})/2\right)}\infty$
. A closed form of the integral can be found for an unstable mode
![]() $\text{arg}(\unicode[STIX]{x1D6FA}g)=\text{arg}\{\unicode[STIX]{x1D714}\left[2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}(1+b)-\unicode[STIX]{x1D714}_{B}\right]/(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}\unicode[STIX]{x1D714}_{B})\}\approx \unicode[STIX]{x03C0}/2$
, for
$\text{arg}(\unicode[STIX]{x1D6FA}g)=\text{arg}\{\unicode[STIX]{x1D714}\left[2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}(1+b)-\unicode[STIX]{x1D714}_{B}\right]/(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}\unicode[STIX]{x1D714}_{B})\}\approx \unicode[STIX]{x03C0}/2$
, for
![]() $\text{Re}[\unicode[STIX]{x1D714}]\rightarrow 0$
. Then,
$\text{Re}[\unicode[STIX]{x1D714}]\rightarrow 0$
. Then,
![]() $\unicode[STIX]{x1D709}\rightarrow \text{e}^{\text{i}\left((3/4)\unicode[STIX]{x03C0}+(\text{argg}\unicode[STIX]{x1D6FA})/2\right)}\infty \approx \text{e}^{\text{i}\left((3/4)\unicode[STIX]{x03C0}+(\unicode[STIX]{x03C0}/4)\right)}\infty =-\infty$
, and
$\unicode[STIX]{x1D709}\rightarrow \text{e}^{\text{i}\left((3/4)\unicode[STIX]{x03C0}+(\text{argg}\unicode[STIX]{x1D6FA})/2\right)}\infty \approx \text{e}^{\text{i}\left((3/4)\unicode[STIX]{x03C0}+(\unicode[STIX]{x03C0}/4)\right)}\infty =-\infty$
, and
![]() $I_{\infty }$
becomes
$I_{\infty }$
becomes
 $$\begin{eqnarray}\displaystyle I_{\infty } & = & \displaystyle \displaystyle -\text{i}\sqrt{\unicode[STIX]{x1D6FA}}\int _{0}^{-\infty }\text{d}\unicode[STIX]{x1D709}\frac{\text{e}^{-\unicode[STIX]{x1D709}^{2}}}{\left(\sqrt{g\unicode[STIX]{x1D6FA}}\right)^{2}-\unicode[STIX]{x1D709}^{2}}\nonumber\\ \displaystyle & = & \displaystyle \text{i}\frac{\sqrt{\unicode[STIX]{x1D6FA}}}{2}\int _{-\infty }^{\infty }\text{d}\unicode[STIX]{x1D709}\frac{\text{e}^{-\unicode[STIX]{x1D709}^{2}}}{2\sqrt{g\unicode[STIX]{x1D6FA}}}\left\{\frac{1}{\unicode[STIX]{x1D709}+\sqrt{\unicode[STIX]{x1D6FA}}}-\frac{1}{\unicode[STIX]{x1D709}-\sqrt{\unicode[STIX]{x1D6FA}}}\right\}\nonumber\\ \displaystyle & = & \displaystyle -\frac{\text{i}}{2}\sqrt{\frac{\unicode[STIX]{x03C0}}{g}}Z(\sqrt{g\unicode[STIX]{x1D6FA}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{\infty } & = & \displaystyle \displaystyle -\text{i}\sqrt{\unicode[STIX]{x1D6FA}}\int _{0}^{-\infty }\text{d}\unicode[STIX]{x1D709}\frac{\text{e}^{-\unicode[STIX]{x1D709}^{2}}}{\left(\sqrt{g\unicode[STIX]{x1D6FA}}\right)^{2}-\unicode[STIX]{x1D709}^{2}}\nonumber\\ \displaystyle & = & \displaystyle \text{i}\frac{\sqrt{\unicode[STIX]{x1D6FA}}}{2}\int _{-\infty }^{\infty }\text{d}\unicode[STIX]{x1D709}\frac{\text{e}^{-\unicode[STIX]{x1D709}^{2}}}{2\sqrt{g\unicode[STIX]{x1D6FA}}}\left\{\frac{1}{\unicode[STIX]{x1D709}+\sqrt{\unicode[STIX]{x1D6FA}}}-\frac{1}{\unicode[STIX]{x1D709}-\sqrt{\unicode[STIX]{x1D6FA}}}\right\}\nonumber\\ \displaystyle & = & \displaystyle -\frac{\text{i}}{2}\sqrt{\frac{\unicode[STIX]{x03C0}}{g}}Z(\sqrt{g\unicode[STIX]{x1D6FA}}).\end{eqnarray}$$
Analytic continuation is needed for damped modes.
Appendix D. The integral
 $I_{g}$
and the Owen
$I_{g}$
and the Owen
 $T$
-function
$T$
-function
In the case of
![]() $I_{g}$
, we have
$I_{g}$
, we have
This integral can be written in terms of the Owen
![]() $T$
-function (Owen Reference Owen1956).
$T$
-function (Owen Reference Owen1956).
 $$\begin{eqnarray}\displaystyle I_{g} & = & \displaystyle \int _{0}^{1/\sqrt{g}}\frac{\text{d}u}{\sqrt{g}}\frac{\text{e}^{\unicode[STIX]{x1D6FA}gu^{2}}}{1+u^{2}}\nonumber\\ \displaystyle & = & \displaystyle \text{e}^{-g\unicode[STIX]{x1D6FA}}\int _{0}^{1/\sqrt{g}}\frac{\text{d}u}{\sqrt{g}}\frac{\exp \left(-\left(\text{i}\sqrt{2g\unicode[STIX]{x1D6FA}}\right)^{2}\left(\displaystyle \frac{u^{2}}{2}+\frac{1}{2}\right)\right)}{1+u^{2}}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x03C0}\frac{\text{e}^{-g\unicode[STIX]{x1D6FA}}}{\sqrt{g}}T\left[\text{i}\sqrt{2g\unicode[STIX]{x1D6FA}};\frac{1}{\sqrt{g}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{g} & = & \displaystyle \int _{0}^{1/\sqrt{g}}\frac{\text{d}u}{\sqrt{g}}\frac{\text{e}^{\unicode[STIX]{x1D6FA}gu^{2}}}{1+u^{2}}\nonumber\\ \displaystyle & = & \displaystyle \text{e}^{-g\unicode[STIX]{x1D6FA}}\int _{0}^{1/\sqrt{g}}\frac{\text{d}u}{\sqrt{g}}\frac{\exp \left(-\left(\text{i}\sqrt{2g\unicode[STIX]{x1D6FA}}\right)^{2}\left(\displaystyle \frac{u^{2}}{2}+\frac{1}{2}\right)\right)}{1+u^{2}}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x03C0}\frac{\text{e}^{-g\unicode[STIX]{x1D6FA}}}{\sqrt{g}}T\left[\text{i}\sqrt{2g\unicode[STIX]{x1D6FA}};\frac{1}{\sqrt{g}}\right].\end{eqnarray}$$
For analytical manipulations and numerical implementation, the most convenient way of writing the Owen function is, perhaps, the following. Since
if we rewrite
 $$\begin{eqnarray}\displaystyle T\left[\text{i}\sqrt{2g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})};\sqrt{\frac{\unicode[STIX]{x1D708}}{g}}\right] & = & \displaystyle \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{\sqrt{\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}}}}\text{d}t\frac{\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})(1+t^{2})}}{1+t^{2}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle =\frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D709}\int _{0}^{\sqrt{\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}}}}\text{d}t\,\text{e}^{-\unicode[STIX]{x1D709}(1+t^{2})}\text{e}^{g\unicode[STIX]{x1D708}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})(1+t^{2})}\nonumber\\ \displaystyle & & \displaystyle \displaystyle =\frac{1}{2\unicode[STIX]{x03C0}}\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D709}\text{e}^{-\unicode[STIX]{x1D709}}\int _{0}^{\sqrt{\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}}}}\text{d}t\,\text{e}^{-(\unicode[STIX]{x1D709}-g(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}))t^{2}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle =\frac{1}{2\unicode[STIX]{x03C0}}\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D709}\text{e}^{-\unicode[STIX]{x1D709}}\sqrt{\frac{\unicode[STIX]{x03C0}/4}{\unicode[STIX]{x1D709}-g_{\unicode[STIX]{x1D708}}\displaystyle \frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}}}\,\text{Erf}\,\sqrt{\unicode[STIX]{x1D708}\left(\frac{\unicode[STIX]{x1D709}}{g_{\unicode[STIX]{x1D708}}}-\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T\left[\text{i}\sqrt{2g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})};\sqrt{\frac{\unicode[STIX]{x1D708}}{g}}\right] & = & \displaystyle \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{\sqrt{\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}}}}\text{d}t\frac{\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})(1+t^{2})}}{1+t^{2}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle =\frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D709}\int _{0}^{\sqrt{\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}}}}\text{d}t\,\text{e}^{-\unicode[STIX]{x1D709}(1+t^{2})}\text{e}^{g\unicode[STIX]{x1D708}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})(1+t^{2})}\nonumber\\ \displaystyle & & \displaystyle \displaystyle =\frac{1}{2\unicode[STIX]{x03C0}}\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D709}\text{e}^{-\unicode[STIX]{x1D709}}\int _{0}^{\sqrt{\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}}}}\text{d}t\,\text{e}^{-(\unicode[STIX]{x1D709}-g(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}))t^{2}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle =\frac{1}{2\unicode[STIX]{x03C0}}\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D709}\text{e}^{-\unicode[STIX]{x1D709}}\sqrt{\frac{\unicode[STIX]{x03C0}/4}{\unicode[STIX]{x1D709}-g_{\unicode[STIX]{x1D708}}\displaystyle \frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}}}\,\text{Erf}\,\sqrt{\unicode[STIX]{x1D708}\left(\frac{\unicode[STIX]{x1D709}}{g_{\unicode[STIX]{x1D708}}}-\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
we are then able to introduce the series representation of the error function, to obtain
 $$\begin{eqnarray}\displaystyle \displaystyle T\left[\text{i}\sqrt{2g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})};\sqrt{\frac{\unicode[STIX]{x1D708}}{g}}\right] & = & \displaystyle \displaystyle \frac{\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\int _{0}^{\infty }\,\text{d}\unicode[STIX]{x1D709}\text{e}^{-\unicode[STIX]{x1D709}}\mathop{\sum }_{n=0}^{\infty }\frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{n!(2n+1)}\left(\unicode[STIX]{x1D709}-g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)^{n}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\mathop{\sum }_{n=0}^{\infty }\frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{n!(2n+1)}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D709}\text{e}^{-\unicode[STIX]{x1D709}}\left(\unicode[STIX]{x1D709}-g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)^{n}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{1}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\mathop{\sum }_{n=0}^{\infty }\frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{n!(2n+1)}\int _{-g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}^{\infty }\text{d}y\,\text{e}^{-y}y^{n}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{1}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\mathop{\sum }_{n=0}^{\infty }\frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{n!(2n+1)}\left(\int _{0}^{\infty }\text{d}y-\int _{0}^{-g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}\text{d}y\right)\text{e}^{-y}y^{n}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{1}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\mathop{\sum }_{n=0}^{\infty }\frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{n!(2n+1)}\left[\unicode[STIX]{x1D6E4}\left(n+1\right)-\unicode[STIX]{x1D6FE}\left(n+1,-g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle T\left[\text{i}\sqrt{2g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})};\sqrt{\frac{\unicode[STIX]{x1D708}}{g}}\right] & = & \displaystyle \displaystyle \frac{\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\int _{0}^{\infty }\,\text{d}\unicode[STIX]{x1D709}\text{e}^{-\unicode[STIX]{x1D709}}\mathop{\sum }_{n=0}^{\infty }\frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{n!(2n+1)}\left(\unicode[STIX]{x1D709}-g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)^{n}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\mathop{\sum }_{n=0}^{\infty }\frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{n!(2n+1)}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D709}\text{e}^{-\unicode[STIX]{x1D709}}\left(\unicode[STIX]{x1D709}-g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)^{n}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{1}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\mathop{\sum }_{n=0}^{\infty }\frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{n!(2n+1)}\int _{-g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}^{\infty }\text{d}y\,\text{e}^{-y}y^{n}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{1}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\mathop{\sum }_{n=0}^{\infty }\frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{n!(2n+1)}\left(\int _{0}^{\infty }\text{d}y-\int _{0}^{-g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}\text{d}y\right)\text{e}^{-y}y^{n}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{1}{2\unicode[STIX]{x03C0}\sqrt{g_{\unicode[STIX]{x1D708}}}}\mathop{\sum }_{n=0}^{\infty }\frac{(-\unicode[STIX]{x1D708}/g_{\unicode[STIX]{x1D708}})^{n}}{n!(2n+1)}\left[\unicode[STIX]{x1D6E4}\left(n+1\right)-\unicode[STIX]{x1D6FE}\left(n+1,-g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
is the incomplete gamma function (Tricomi Reference Tricomi1950a
,Reference Tricomi
b
). Tricomi shows that, for integer
![]() $n$
,
$n$
,
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}\left(n+1,-g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)=n!\left[1-\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}\mathop{\sum }_{m=0}^{n}\frac{\left(-g_{\unicode[STIX]{x1D708}}\displaystyle \frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)^{m}}{m!}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}\left(n+1,-g_{\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)=n!\left[1-\text{e}^{g_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}})}\mathop{\sum }_{m=0}^{n}\frac{\left(-g_{\unicode[STIX]{x1D708}}\displaystyle \frac{\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}}\right)^{m}}{m!}\right],\end{eqnarray}$$
therefore, our series representation of the Owen function is
Appendix E. Proof of some identities
In appendix B, we derived the following result
which is valid
![]() $\forall$
$\forall$
![]() $b$
. We now prove that, for
$b$
. We now prove that, for
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}\equiv \unicode[STIX]{x1D714}_{B}$
,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}\equiv \unicode[STIX]{x1D714}_{B}$
,
where
is the result found by BDR (Biglari et al. Reference Biglari, Diamond and Rosenbluth1989).
Since
![]() $\lim _{b\rightarrow 0}g=1$
, we have
$\lim _{b\rightarrow 0}g=1$
, we have
where
It is easy to see that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(x) & = & \displaystyle \displaystyle \frac{\text{i}}{2\sqrt{\unicode[STIX]{x03C0}}}\int _{-\infty }^{\unicode[STIX]{x1D6FA}}\text{d}z\frac{\text{e}^{-z}}{z^{1/2}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{\text{i}}{2\sqrt{\unicode[STIX]{x03C0}}}\text{e}^{\unicode[STIX]{x1D6FA}}F_{1,1}^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(x) & = & \displaystyle \displaystyle \frac{\text{i}}{2\sqrt{\unicode[STIX]{x03C0}}}\int _{-\infty }^{\unicode[STIX]{x1D6FA}}\text{d}z\frac{\text{e}^{-z}}{z^{1/2}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{\text{i}}{2\sqrt{\unicode[STIX]{x03C0}}}\text{e}^{\unicode[STIX]{x1D6FA}}F_{1,1}^{1/2}.\end{eqnarray}$$
Then
 $$\begin{eqnarray}\displaystyle \lim _{b\rightarrow 0}R & = & \displaystyle 2\text{i}\sqrt{\unicode[STIX]{x03C0}}\text{e}^{-\unicode[STIX]{x1D6FA}}Z(\sqrt{\unicode[STIX]{x1D6FA}})+4\unicode[STIX]{x03C0}\text{e}^{-2\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D6F7}(\text{i}\sqrt{2\unicode[STIX]{x1D6FA}})[1-\unicode[STIX]{x1D6F7}(\text{i}\sqrt{2\unicode[STIX]{x1D6FA}})],\nonumber\\ \displaystyle & = & \displaystyle 2\text{i}\sqrt{\unicode[STIX]{x03C0}}\text{e}^{-\unicode[STIX]{x1D6FA}}\{Z(\sqrt{\unicode[STIX]{x1D6FA}})+F_{1,1}^{1/2}\}+F_{1,1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{b\rightarrow 0}R & = & \displaystyle 2\text{i}\sqrt{\unicode[STIX]{x03C0}}\text{e}^{-\unicode[STIX]{x1D6FA}}Z(\sqrt{\unicode[STIX]{x1D6FA}})+4\unicode[STIX]{x03C0}\text{e}^{-2\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D6F7}(\text{i}\sqrt{2\unicode[STIX]{x1D6FA}})[1-\unicode[STIX]{x1D6F7}(\text{i}\sqrt{2\unicode[STIX]{x1D6FA}})],\nonumber\\ \displaystyle & = & \displaystyle 2\text{i}\sqrt{\unicode[STIX]{x03C0}}\text{e}^{-\unicode[STIX]{x1D6FA}}\{Z(\sqrt{\unicode[STIX]{x1D6FA}})+F_{1,1}^{1/2}\}+F_{1,1}.\end{eqnarray}$$
However, it is also true that
 $$\begin{eqnarray}\displaystyle F_{1,1}^{1/2} & = & \displaystyle \text{e}^{-\unicode[STIX]{x1D6FA}}\int _{-\infty }^{\unicode[STIX]{x1D6FA}}\text{d}z\frac{\text{e}^{-z}}{z^{1/2}}\nonumber\\ \displaystyle & = & \displaystyle -2\text{i}\text{e}^{-\unicode[STIX]{x1D6FA}}\int _{-\infty }^{\text{i}\unicode[STIX]{x1D6FA}^{1/2}}\text{d}t\,\text{e}^{-t^{2}}\nonumber\\ \displaystyle & = & \displaystyle -Z(\sqrt{\unicode[STIX]{x1D6FA}}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{1,1}^{1/2} & = & \displaystyle \text{e}^{-\unicode[STIX]{x1D6FA}}\int _{-\infty }^{\unicode[STIX]{x1D6FA}}\text{d}z\frac{\text{e}^{-z}}{z^{1/2}}\nonumber\\ \displaystyle & = & \displaystyle -2\text{i}\text{e}^{-\unicode[STIX]{x1D6FA}}\int _{-\infty }^{\text{i}\unicode[STIX]{x1D6FA}^{1/2}}\text{d}t\,\text{e}^{-t^{2}}\nonumber\\ \displaystyle & = & \displaystyle -Z(\sqrt{\unicode[STIX]{x1D6FA}}),\end{eqnarray}$$
then the first two terms in equation (E 7) cancel, leaving us with
which is what we aimed to prove.
Appendix F. Real frequency at marginality, long-wavelength limit
 $b\rightarrow 0$
$b\rightarrow 0$
In the light of the identities just proved in appendix E, we are in the position to say that, for
![]() $b\rightarrow 0$
,
$b\rightarrow 0$
,
 $$\begin{eqnarray}\displaystyle D & \equiv & \displaystyle -\left(1+\unicode[STIX]{x1D70F}\right)+I_{i}\nonumber\\ \displaystyle & = & \displaystyle -\left(1+\unicode[STIX]{x1D70F}\right)+\left(1-\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\right)\unicode[STIX]{x1D6FA}Z^{2}(\sqrt{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D702}_{i}\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\{(1-2\unicode[STIX]{x1D6FA})\unicode[STIX]{x1D6FA}Z^{2}(\sqrt{\unicode[STIX]{x1D6FA}})-2\unicode[STIX]{x1D6FA}^{3/2}Z(\sqrt{\unicode[STIX]{x1D6FA}})\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D & \equiv & \displaystyle -\left(1+\unicode[STIX]{x1D70F}\right)+I_{i}\nonumber\\ \displaystyle & = & \displaystyle -\left(1+\unicode[STIX]{x1D70F}\right)+\left(1-\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\right)\unicode[STIX]{x1D6FA}Z^{2}(\sqrt{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D702}_{i}\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\{(1-2\unicode[STIX]{x1D6FA})\unicode[STIX]{x1D6FA}Z^{2}(\sqrt{\unicode[STIX]{x1D6FA}})-2\unicode[STIX]{x1D6FA}^{3/2}Z(\sqrt{\unicode[STIX]{x1D6FA}})\},\end{eqnarray}$$
which corresponds to
![]() $D_{0}$
in (3) of BDR (Biglari et al.
Reference Biglari, Diamond and Rosenbluth1989). The real frequency at marginality is evaluated by solving
$D_{0}$
in (3) of BDR (Biglari et al.
Reference Biglari, Diamond and Rosenbluth1989). The real frequency at marginality is evaluated by solving
![]() $\text{Im}[D(\unicode[STIX]{x1D714}_{r})]\equiv D_{i}(\unicode[STIX]{x1D714}_{r})=0$
, where we set
$\text{Im}[D(\unicode[STIX]{x1D714}_{r})]\equiv D_{i}(\unicode[STIX]{x1D714}_{r})=0$
, where we set
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D6FE}$
, and take
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D6FE}$
, and take
![]() $\unicode[STIX]{x1D6FE}\rightarrow 0$
. This comes directly from (F 1)
$\unicode[STIX]{x1D6FE}\rightarrow 0$
. This comes directly from (F 1)
As a validity check, one can set
![]() $J_{0}^{2}\rightarrow 1$
in the definition of
$J_{0}^{2}\rightarrow 1$
in the definition of
![]() $I_{i}$
and integrate the resonances in yet another way. Thus
$I_{i}$
and integrate the resonances in yet another way. Thus
 $$\begin{eqnarray}\displaystyle I_{i} & = & \displaystyle \displaystyle 2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }\text{e}^{-\hat{v}_{\bot }^{2}}\int _{-\infty }^{\infty }\frac{\text{d}\hat{v}_{\Vert }\text{e}^{-\hat{v}_{\bot }^{2}}}{\sqrt{\unicode[STIX]{x03C0}}}\frac{\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}_{\ast }\left[1+\unicode[STIX]{x1D702}_{i}\left(\hat{v}_{\Vert }^{2}+\hat{v}_{\bot }^{2}-3/2\right)\right]}{\unicode[STIX]{x1D6FA}-\left(\hat{v}_{\Vert }^{2}+\hat{v}_{\bot }^{2}\right)}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle -2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }\text{e}^{-\hat{v}_{\bot }^{2}}\left\{\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}_{\ast i}\left(1-\frac{3}{2}\unicode[STIX]{x1D702}_{i}\right)\frac{Z\left(\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}\right)}{\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}}\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D702}_{i}\unicode[STIX]{x1D6FA}_{\ast i}\left\{1+2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }^{3}\text{e}^{-\hat{v}_{\bot }^{2}}\frac{Z\left(\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}\right)}{\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}}\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D702}_{i}\unicode[STIX]{x1D6FA}_{\ast i}2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }\text{e}^{-\hat{v}_{\bot }^{2}}\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}Z\left(\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{i} & = & \displaystyle \displaystyle 2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }\text{e}^{-\hat{v}_{\bot }^{2}}\int _{-\infty }^{\infty }\frac{\text{d}\hat{v}_{\Vert }\text{e}^{-\hat{v}_{\bot }^{2}}}{\sqrt{\unicode[STIX]{x03C0}}}\frac{\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}_{\ast }\left[1+\unicode[STIX]{x1D702}_{i}\left(\hat{v}_{\Vert }^{2}+\hat{v}_{\bot }^{2}-3/2\right)\right]}{\unicode[STIX]{x1D6FA}-\left(\hat{v}_{\Vert }^{2}+\hat{v}_{\bot }^{2}\right)}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle -2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }\text{e}^{-\hat{v}_{\bot }^{2}}\left\{\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}_{\ast i}\left(1-\frac{3}{2}\unicode[STIX]{x1D702}_{i}\right)\frac{Z\left(\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}\right)}{\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}}\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D702}_{i}\unicode[STIX]{x1D6FA}_{\ast i}\left\{1+2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }^{3}\text{e}^{-\hat{v}_{\bot }^{2}}\frac{Z\left(\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}\right)}{\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}}\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D702}_{i}\unicode[STIX]{x1D6FA}_{\ast i}2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }\text{e}^{-\hat{v}_{\bot }^{2}}\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}Z\left(\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}\right).\end{eqnarray}$$
It is easy to see that
 $$\begin{eqnarray}\displaystyle \displaystyle 2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }^{3}\text{e}^{-\hat{v}_{\bot }^{2}}\frac{Z(\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2})}{\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}} & = & \displaystyle \displaystyle 2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }2\hat{v}_{\bot }\left(\frac{\hat{v}_{\bot }^{2}}{2}-\unicode[STIX]{x1D6FA}+\unicode[STIX]{x1D6FA}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \times \,\text{e}^{-\hat{v}_{\bot }^{2}}\frac{Z(\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2})}{\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle 2\unicode[STIX]{x1D6FA}I_{1}+2(-4\text{i})\text{e}^{-2\unicode[STIX]{x1D6FA}}\int _{\text{i}\unicode[STIX]{x1D6FA}^{1/2}}^{\infty }\text{d}\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}^{2}\text{e}^{-2\unicode[STIX]{x1D701}^{2}}Z\left(\text{i}\unicode[STIX]{x1D701}\right)\nonumber\\ \displaystyle & \equiv & \displaystyle \displaystyle 2\unicode[STIX]{x1D6FA}I_{1}+2I_{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle 2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }\hat{v}_{\bot }^{3}\text{e}^{-\hat{v}_{\bot }^{2}}\frac{Z(\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2})}{\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}} & = & \displaystyle \displaystyle 2\int _{0}^{\infty }\text{d}\hat{v}_{\bot }2\hat{v}_{\bot }\left(\frac{\hat{v}_{\bot }^{2}}{2}-\unicode[STIX]{x1D6FA}+\unicode[STIX]{x1D6FA}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \times \,\text{e}^{-\hat{v}_{\bot }^{2}}\frac{Z(\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2})}{\sqrt{\unicode[STIX]{x1D6FA}-\hat{v}_{\bot }^{2}/2}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle 2\unicode[STIX]{x1D6FA}I_{1}+2(-4\text{i})\text{e}^{-2\unicode[STIX]{x1D6FA}}\int _{\text{i}\unicode[STIX]{x1D6FA}^{1/2}}^{\infty }\text{d}\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}^{2}\text{e}^{-2\unicode[STIX]{x1D701}^{2}}Z\left(\text{i}\unicode[STIX]{x1D701}\right)\nonumber\\ \displaystyle & \equiv & \displaystyle \displaystyle 2\unicode[STIX]{x1D6FA}I_{1}+2I_{2},\end{eqnarray}$$
and
Then
By writing the plasma dispersion function as an error function of imaginary argument, one sees that the integrals
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
can be performed analytically to obtain
$I_{2}$
can be performed analytically to obtain
 $$\begin{eqnarray}\displaystyle 1+\unicode[STIX]{x1D70F} & = & \displaystyle \left\{-\left(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}_{\ast i}\right)-\unicode[STIX]{x1D702}_{i}\unicode[STIX]{x1D6FA}_{\ast i}\left(1-2\unicode[STIX]{x1D6FA}\right)\right\}\unicode[STIX]{x03C0}\text{e}^{-2\unicode[STIX]{x1D6FA}}\Bigl[1-\text{Erf}\,i^{2}(\sqrt{\unicode[STIX]{x1D6FA}})-2\text{i}\,\text{Erf}\,i(\sqrt{\unicode[STIX]{x1D6FA}})\Bigr]\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D702}_{i}\unicode[STIX]{x1D6FA}_{\ast i}\sqrt{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FA}}\text{e}^{-\unicode[STIX]{x1D6FA}}[\text{Erf}\,i(\sqrt{\unicode[STIX]{x1D6FA}})+i],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1+\unicode[STIX]{x1D70F} & = & \displaystyle \left\{-\left(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}_{\ast i}\right)-\unicode[STIX]{x1D702}_{i}\unicode[STIX]{x1D6FA}_{\ast i}\left(1-2\unicode[STIX]{x1D6FA}\right)\right\}\unicode[STIX]{x03C0}\text{e}^{-2\unicode[STIX]{x1D6FA}}\Bigl[1-\text{Erf}\,i^{2}(\sqrt{\unicode[STIX]{x1D6FA}})-2\text{i}\,\text{Erf}\,i(\sqrt{\unicode[STIX]{x1D6FA}})\Bigr]\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D702}_{i}\unicode[STIX]{x1D6FA}_{\ast i}\sqrt{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FA}}\text{e}^{-\unicode[STIX]{x1D6FA}}[\text{Erf}\,i(\sqrt{\unicode[STIX]{x1D6FA}})+i],\end{eqnarray}$$
whose imaginary part set to zero gives (F 2).