Introduction
It is now generally accepted that where a glacier is well coupled to a basal till layer, deformation of that layer can contribute to flow, and that in some cases this contribution may be significant. However, in order to comprehend fully the role of basal till in glacier dynamics, knowledge of its mechanical properties and the associated basal drainage network are required (Reference Boulton and DobbieBoulton and Dobbie, 1998). Attempts have been made to formulate rheological relations to predict the strain response of till to an applied stress, usually assuming either viscous (e.g. Reference Boulton and HindmarshBoulton and Hindmarsh, 1987) or plastic (e.g. Reference KambKamb, 1991; Reference Tulaczyk, Mickelson and AttigTulaczyk, 1999) behaviour. Which of these rheological models best describes the mechanical properties of basal till is a source of debate; recent laboratory experiments (e.g. Reference Iverson, Hooyer and BakerIverson and others, 1998) suggest that till deforms as a plastic solid. However, there are indications that at larger scales, till may deform as a viscous fluid (Reference HindmarshHindmarsh, 1997). Increased understanding of the properties of basal till has been hampered by the scarcity of data from in situ observations of the deformation process beneath a reasonable ice thickness. In particular, the exact nature of relationships between deformation and water-pressure fluctuations within the basal till layer remains obscure, and yet assumed relationships between these two variables are often inherent in rheological models used to predict the strain response of till to applied stress. Greater understanding of the mechanical and hydraulic properties of basal till is important not only for increasing our understanding of the dynamics of present-day ice masses, but also for attempts to model the behaviour and interpret the sedimentary signatures of former ice masses. In this paper we present the results of simultaneous monitoring of deformation rates and pore-water pressure variations within the basal till layer, together with borehole water pressure beneath 60–140 m of ice at Bakaninbreen, southern Svalbard.
Field Site
Bakaninbreen is a 17 km long valley glacier that in 1995–96 was in the late phase of a surge thought to have begun between the springs of 1985 and 1986 (Reference Dowdeswell, Hamilton and HagenDowdeswell and others, 1991; Fig. 1a). A surge front formed where fast-moving surge ice buttressed non-surge ice (Fig. 1b). Through a combination of extensive hot-water drilling, subglacial instrumentation and direct sampling of basal sediments, the lower reaches of the glacier have been shown to overlie a mixture of glaciomarine muds and till thought to be at least 0.2–0.3 m thick (Reference Hambrey, Dowdeswell, Murray and PorterHambrey and others, 1996). Basal sediment samples retrieved at Bakaninbreen invariably consist largely of silts and clays with a small amount of coarser material, including occasional striated and rounded clasts. These samples show peaks at 3–5.5φ (0.125–0.023 mm). However, the sampling technique excludes larger particles, and the bed material is probably texturally similar to sediment uplifted along faults in the glacier surface described by Reference Hambrey, Dowdeswell, Murray and PorterHambrey and others (1996). Data from sliding sensors installed beneath the glacier show enhanced sliding rates up-glacier of the surge front, and comparison of till-strength estimates gained from borehole ploughmeters with calculated shear stress suggests that deformation of the till layer is occurring in this region (Reference Porter, Murray and DowdeswellPorter and others, 1997). In contrast, the sliding rate is very low down-glacier of the surge front (Reference PorterPorter, 1997).
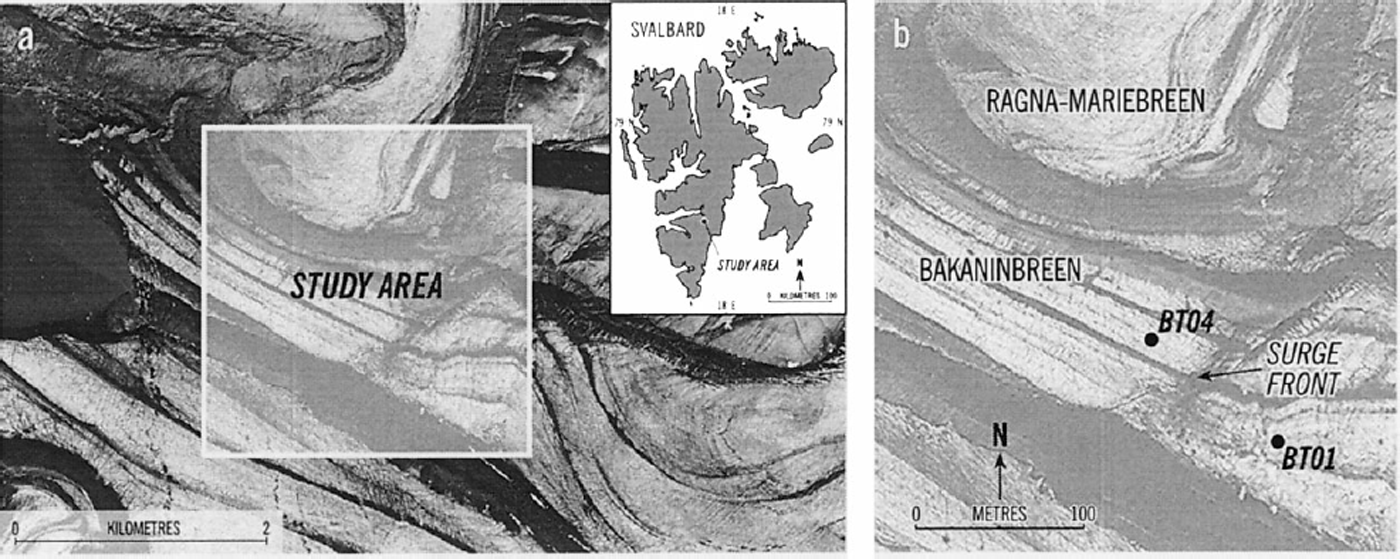
Fig 1. Field study site, (a) Location map of the Svalbard archipelago superimposed upon a Norwegian Polar Institute aerial photograph of the lower reaches of Bakaninbreen taken in 1990. (b) Close-up of the surge front showing approximate locations of tiltsensor strings BT01 and BT04. (Aerial photograph No. S90 6825 © Norwegian Polar Institute)
Ground-penetrating radar (GPR) surveys (Reference Murray, Gooch and StuartMurray and others, 1997, Reference Murray2000) revealed the region of the ice–bed interface at Bakaninbreen to be complex. Together with drilling depths, these surveys indicate a layer of sediment-rich basal ice, 5–22 m thick (Reference MurrayMurray and others, 2000). Several extensive englacial reflectors are thought to be debris-rich faults, also identified through structural mapping (Reference Hambrey, Dowdeswell, Murray and PorterHambrey and others, 1996), some of which crop out in the region of the surge front, while others terminate englacially (Reference Murray, Gooch and StuartMurray and others, 1997). These faults are thought to be responsible for bringing basal debris to the surface of the glacier, and have been observed to drain water during hot-water drilling (Reference Hambrey, Dowdeswell, Murray and PorterHambrey and others, 1996). Surface velocities during 1995 were ∼1.8 to 3.0 m a−1 above the surge front and 0.1–0.6 m a−1 below the surge front (personal communication from D. Orton, 1995).
The thermal regime of Bakaninbreen is spatially variable, and the location of the surge front is thought to mark the transition between warm and cold ice at the bed (Reference MurrayMurray and others, 2000). Down-glacier of the surge front, where ice is 60–70 m thick, borehole thermistors indicate cold ice throughout. Up-glacier of the surge front, the ice is >100 m thick, and cold surface ice overlies ice at the pressure-melting point at depths deeper than 60–70 m (Reference MurrayMurray and others, 2000).
Methods
In order to assess rates of deformation within the till layer directly, two strings of tilt sensors were installed into the sedimentary bed during 1995. String BT01 was installed up-glacier (in a borehole 140 m deep that drained to 23 m below the ice surface) and string BT04 down-glacier (in an unconnected borehole 61 m deep) of the surge front (Fig. 1b). The tilt-cell strings were driven into the basal till using a percussion hammer as described by Reference Blake, Clarke and GérinBlake and others (1992). The depths of insertion resulting from hammering were 0.1 m for BT04 and 0.2 m for BT01.
It is always difficult to assess the location of the sensor relative to the ice–bed interface, not least because of its expected complexity. For example, where the bed is cold, the sediment-rich basal ice may grade into ice-rich sediment without a clear boundary. Drilling is likely to melt ice, creating a void and releasing sediment stored in the basal ice, as well as potentially excavating basal sediment. Furthermore, sediment may flow from the bed into the borehole, and this together with sediment released from basal ice raises the potential for sensors to be installed in till but within the body of the glacier.
At Bakaninbreen, the likely sediment content of the basal ice layer is <10% by volume, meaning that drilling the borehole will release somewhat less than 0.5–2 m of sediment from the basal ice. In an undrained borehole (such as the hole into which BT04 was installed) the bed is over-pressured and till will not flow into the borehole from the bed. For a drained borehole (such as the hole into which BT01 was installed) till may flow from the bed into the borehole. Our observations during drilling, which show that the drill stem and hose are caked in sediment on retrieval to a height of several metres, and that borehole water is extremely turbid during the last stages of drilling, give an indication that both of these effects probably do occur.
However, despite these observations we consider our sensors to be emplaced in sediments below the ice–bed interface and not within the glacier ice. Our main evidence for this assertion comes from drag-spools (e.g. Reference Blake, Fischer and ClarkeBlake and others, 1994) and ploughmeters (e.g. Reference Fischer and ClarkeFischer and Clarke, 1994). In order to record sliding, drag-spools require separation of the anchor from the spool. This cannot happen if the instruments are installed within the glacier ice, yet we consistently recorded string payout representing sliding rates of ∼1 to 8 × 10−4 m d−1 above the surge front at Bakaninbreen (Reference PorterPorter, 1997). Equally, ploughmeters do not record a force unless they are partially trapped within the glacier but their tip is installed in the bed. Again we record forcings on these instruments at Bakaninbreen that can only be explained by their insertion into basal sediments below the ice–bed interface (Reference Porter, Murray and DowdeswellPorter and others, 1997). Therefore, we believe the disturbed till, which enters the borehole by melting from basal ice or flowage, to be soft and easily penetrable by the combined weight of the instruments, insertion tool plus hammer at this site. Furthermore, we believe our measurements of insertion during hammering are minimum values for the insertion depth as we believe that the instruments settle into the till to some unknown depth (e.g. Reference Blake, Clarke and GérinBlake and others, 1992). The above discussion suggests that some of this uncertainty could be eliminated by instrumenting unconnected rather than connected holes with sensors designed to be installed into the sub-basal till layer. The alternate possibility of attempting to maintain water pressure in a connected hole is impossible at most sites.
Ideally a large amount of slack wire should be present at the ice–bed interface so that glacier sliding would not interfere with measurement of till strain rates. However, immediately after insertion the till is very soft, and we found that feeding excess wire down the borehole caused the sensors to fall over. As a result, the slack wire available was probably limited to a few centimetres (certainly less than a decimetre). A pressure transducer was installed in each borehole approximately 0.5 m above the ice–till interface (Trans-Instruments part number 2000AAB25C1A00A).
Description of the sensor
The tilt sensors used in this study were built around a commercial dual axis electrolytic cell (Fredericks Company part number 0717-2201; Fig. 2a). Tilt sensors consisted of a string of two cells, each cell being housed in a resin-filled plastic cylinder of outside dimensions 18 mm in diameter and 70 mm in height. The lower cell in each string was equipped with an integral pore-pressure transducer (SensorTechnics part number 15U300GC) housed behind a porous plastic membrane (Fig. 2a). The cells were connected by flexible signal wires, and the centre–centre spacing between each cell was 0.12 m. Calibration of each tilt cell used a jig that allowed tilting through the maximum tilt range of ±70° and rotation through 180°. Each cell has two voltage outputs, V 1 and V 2, from pairs of perpendicular electrodes (Fig. 2b), which were fitted simultaneously to surfaces, P 1 and P 2, of the form
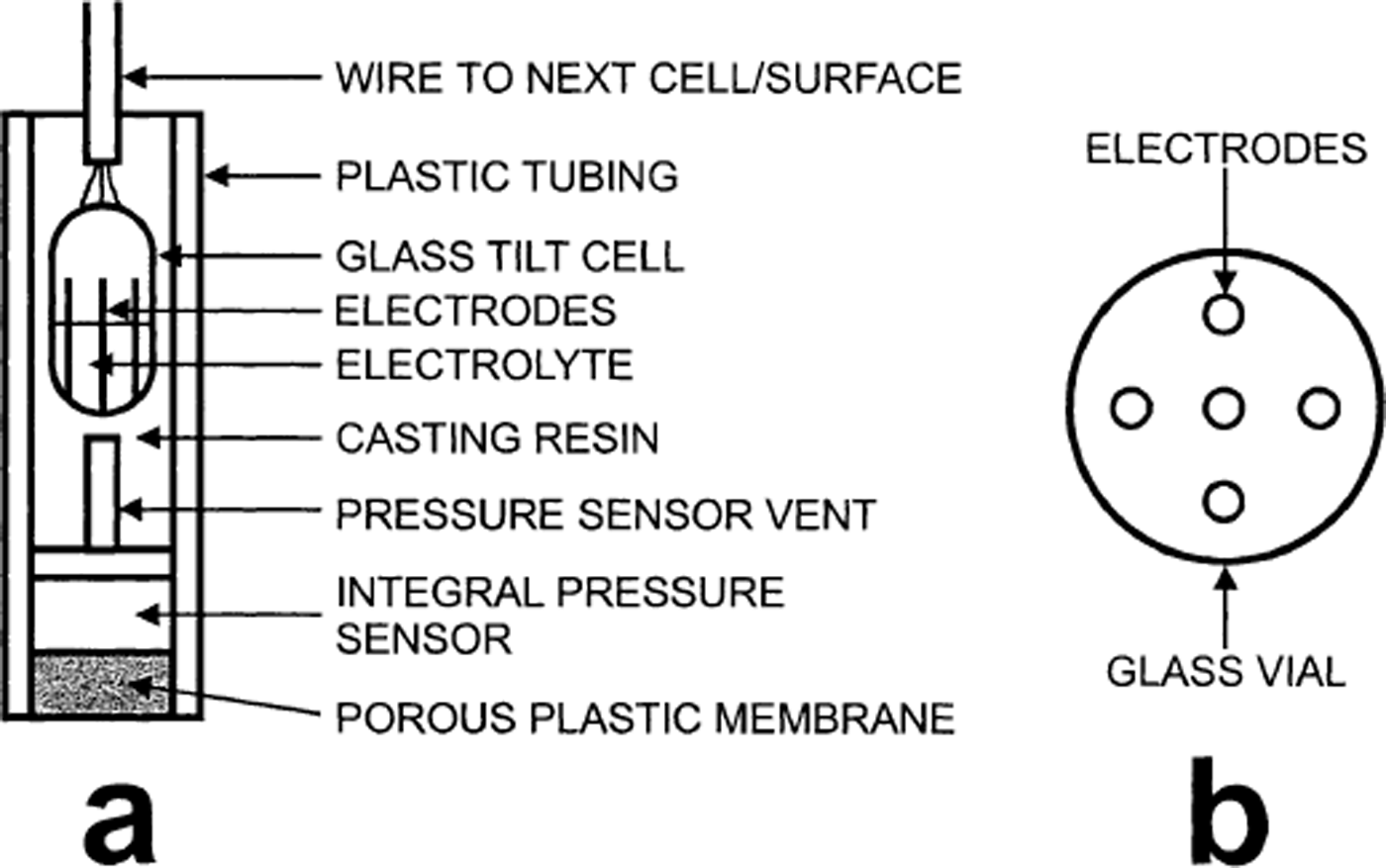
Fig. 2. (a) Diagram of electrolytic tilt sensor, (b) Plan view of dual-axis electrode configuration.
where θ is the tilt angle, φ is the azimuth angle, the constants Ai scale the amplitudes of the predicted output at each tilt angle, B reflects the arbitrary choice of the tilt sensor zero for rotation, G accounts for non-vertical alignment of the tilt cell in the resin, and Ci represents the output at zero tilt (after Reference Blake, Clarke and GérinBlake and others, 1992). Surfaces were fitted simultaneously for both cell outputs to minimize the fitting parameter E:

Following the analysis of Reference Blake, Clarke and GérinBlake and others (1992), we decomposed raw tilt data into down-flow and cross-flow components by assuming that the mean tilt azimuth was aligned with ice flow. However, our records indicated that azimuth drifted over long periods, and so decomposition was performed using the mean azimuth over 30 day segments of the record. The down-flow tilt records were smoothed using a Gaussian filter with a standard deviation of 12 hours, and the strain rate was then calculated using the method described by Reference Blake, Clarke and GérinBlake and others (1992).
Results
Strain rates within the basal till layer
The strain rates recorded up-glacier (mean 0.44 a−1) of the surge front were an order of magnitude higher than those recorded down-glacier (mean 0.04 a−1) of it (Table 1). These mean strain rates integrated over the measured insertion depth represent rather less than 10% of the observed surface motion. All the strain-rate records showed periods of zero, negative (i.e. up-glacier) and rapidly fluctuating strain rate (Fig. 3). In general, the strain-rate records exhibited a lack of correspondence between the upper and lower cell in each string (Fig. 3). This particularly seems to be the case for string BT01 (Fig. 3a and b). String BT04 (Fig. 3c and d) shows closer correspondence between upper and lower sensors, particularly during summer 1996 when the strain-rate signal also becomes characterized by high-magnitude, high-frequency variations. The upper cell in each string experienced a higher mean strain rate than the lower cell (Table 1), although the difference is less marked in string BT01 installed up-glacier of the surge front.
Table 1. Mean strain rates and till-viscosity estimates from tiltcell strings BT01 (up-glacier) and BT04 (down-glacier) of the surge front. L denotes lower and U the upper cell of each string


Fig. 3. Strain-rate data from tilt sensors installed beneath Bakaninbreen. Grey lines show strain rate; black lines show cumulative mean strain rate.
It is important to identify the time-span over which our sensors gave reliable data. Our sensors are limited to a maximum tilt angle of 70°. In a deforming till, differential motion between the cell top and base will tilt the cell, such that
where x′ and x are horizontal coordinates of the top of the tilt cell after and before deformation respectively, y is height of the tilt cell, and ψ is the angular shear. Thus, assuming that the glacier is well coupled to the basal till, and that deformation is the dominant form of basal motion, the sensors will fail by progressively tilting to angles of >70°. If, however, the glacier slides over its bed, the wire connecting the sensors will progressively pull the cells out of the till. In this case, the sensors will eventually be pulled along the ice–bed interface at a high angle (but not necessarily >70°). When the tilt cell is responding to deformation, we expect the mean strain rate to be non-zero, and that the overall motion of the cell is in the down-glacier direction. In contrast, a cell that is being towed at the ice–bed interface would be expected to have a tilt angle that fluctuates around a constant value. The time series should therefore be truncated when either (i) the cell goes off-range (tilt > 70°) or (ii) the mean of the strain rate for either of the cells of a string becomes effectively zero (Fig. 3). All our cells meet the latter criterion at an angle which is < 70°, i.e. it appears that glacier sliding progressively pulls them out of the till layer so that eventually the strain rate becomes zero. Using this criterion, string BT01 (up-glacier of the surge front) is deemed to be responding to deformation of the till layer for 130 days, until January/February 1996 (Fig. 3a and b), whereas string BT04 (down-glacier of the surge front) is thought to be responding to deformation for over a year, until late 1996 (Fig. 3c and d).
Borehole and till water-pressure fluctuations
The pore-water and corresponding borehole water pressures are shown in Figure 4. The pore-water pressure transducer installed up-glacier of the surge front worked successfully for a period of approximately 4 months, after which the signal failed abruptly and we assume one of the signal wires was broken. The pore-water pressure transducer down-glacier of the surge front did not fail in this manner. However, after a similar period the measured pressure rapidly rose to above the ice overburden pressure, and so we have truncated the time series when this rise occurs. The borehole pressure transducers worked without difficulty during this time period.

Fig. 4. Water-pressure data from borehole and pore-pressure sensors at Bakaninbreen; grey lines show borehole water-pressure fluctuations; black lines show water-pressure fluctuations within the till layer.
There are two notable characteristics of these pressure observations. First, borehole water pressure almost always exceeded the pressure measured in the till layer (Fig. 4). This observation is counter-intuitive because the borehole transducer is installed above the pore-water transducer by approximately 0.5 m. This could result from the refreezing of the borehole forcing water into the bed, a process that Reference Waddington and ClarkeWaddington and Clarke (1995) described as freeze-forcing. Second, although borehole water pressure and pore-water pressure track each other in their large-scale features, the pore-water pressure shows a great deal of fine detail that is not shared by the borehole water pressure. While it appears that the overall forcing for both traces is similar, there are processes occurring within the till layer, such as dilation or consolidation, that superimpose a high-frequency, and probably localized, component.
Mechanical Properties of Basal Sediments
Basal dynamics
Because of the necessity of having physical connections between tilt sensors, any glacier sliding must inevitably result in some interference with the motion of tilt sensors in response to deformation of the till layer. This effect is difficult to quantify. However, if angular changes registered by tilt sensors after insertion are assumed to arise solely due to progressive removal from the till layer as a result of basal sliding rather than cumulative strain, then it is possible to gain an estimate of mean basal sliding rates. The minimum depth of installation of tilt sensors into the basal till layer is monitored during insertion, and the distance between individual tilt sensors in each string is also known. By application of simple trigonometry and assuming a straight-line path between the position at the time of insertion and that at instrument failure, the angular change of tilt sensors with respect to time can be resolved into a horizontal displacement.
Applying such a calculation and then taking the resultant mean displacement from each string yields a sliding rate of 2.0 × 10−3 m d−1 up-glacier of the surge front and 9.0 × 10−5 m d−1 down-glacier of it. The sliding rate up-glacier of the surge front calculated from these tilt-cell data compares with a mean sliding rate over the period November 1994 to mid-April 1995, of 1.2 × 10 to 2.5 × 10−6 m d−1 measured by drag-spools installed in the same location (Reference PorterPorter, 1997). Drag-spools installed down-glacier of the surge front show sliding rates of 1 × 10−6 to 7 × 10−6 m d−1 during the same period (Reference PorterPorter, 1997). However, the errors associated with sliding rates calculated from tilt-sensor data are potentially significant, primarily because of uncertainties of sensor placement with respect to the ice–bed interface. As discussed above and in common with Reference Blake, Clarke and GérinBlake and others (1992), we believe that the depth of installation of tilt sensors into the till layer must be regarded as a minimum: increasing the insertion depth in our calculation of sliding rate has the result of increasing the sliding rate calculated from tilt-sensor data; sliding rates calculated from tilt-cell data should therefore be regarded as minimum values.
Thus, our tilt sensors are indicating substantially (order-of-magnitude) higher sliding rates than measurements using drag-spools over the same time period. Given that drag-spools are thought to record a maximum sliding rate, because of the possibility of deformation within the till layer between the instrument anchor and the ice–bed interface (Reference Blake, Fischer and ClarkeBlake and others, 1994), the higher sliding rate calculated from tilt-sensor data seems improbable. This leads us to the conclusion that movement registered by our tilt sensors must arise from a combination of deformation within the till layer, and withdrawal from the till layer as a result of basal sliding, with deformation being the dominant component of flow. Differentiating the contribution of the two components more precisely is clearly problematic given our inability to quantify errors of sensor placement.
Strain rates within the basal till layer
During the late phase of the surge, Bakaninbreen exhibits a more dynamic flow regime up-glacier of the surge front than down-glacier of it, whether we attribute data gained from tilt sensors to sliding or deformation of the till layer, or a combination of both components. Negative (up-glacier) and fluctuating strain rates are a common feature exhibited by all tilt sensors installed beneath Bakaninbreen (Fig. 3). Tilt sensors installed within the basal till layer at Trapridge Glacier, Canada (Reference Blake, Clarke and GérinBlake and others, 1992), and Storglaciaren, Sweden (Reference Iverson, Hanson, Hooke and JanssonIverson and others, 1995; Reference Hooke, Hanson, Iverson, Jansson and FischerHooke and others, 1997), generated datasets displaying similar features. Negative strain rates occur when the cell is tilted in an up-glacier direction or the lower end of the tilt sensor is experiencing faster displacement relative to the top of the sensor (Reference Blake, Clarke and GérinBlake and others, 1992). Several explanations have been put forward to explain this phenomenon. If ice is decoupled from the bed, elastic up-glacier movement of the upper till layer could occur, with resultant negative strain rates (Reference Hooke, Hanson, Iverson, Jansson and FischerHooke and others, 1997). Similarly, dilation and consolidation of the till layer may cause its thickening or thinning and hence negative strain rates (Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000). Interaction between tilt sensor and clastic material within the deforming till layer may also result in negative strain rates being recorded. Movement of clasts may create void spaces within the till matrix, and the tilt sensor may be tilted as matrix material moves to fill these void spaces, again potentially in an up-glacier direction. Folding or faulting may occur, tilting the cell up-glacier (Reference Boulton and DobbieBoulton and Dobbie, 1998). Finally, propagation of changes in water pressure through the till layer may result in enhanced deformation lower in the till layer, causing the lower end of the cell to be displaced more rapidly than the upper end and hence negative strain rates (Reference Tulaczyk, Mickelson and AttigTulaczyk, 1999).
Our tilt cells show a general lack of correspondence between cells on the same string (Fig. 3), which is in contrast to observations made elsewhere where tilt sensors have been observed to move almost simultaneously (Reference Blake, Clarke and GérinBlake and others, 1992). This could result from inhomogeneous deformation such as folding (Reference Boulton and DobbieBoulton and Dobbie, 1998) or faulting (Reference Truffer, Harrison and EchelmeyerTruffer and others, 2000) within the till layer.
Till rheology
In order to assess the rheologic properties of till, an appropriate rheometric model is required. This involves making some assumption regarding the physical properties and behaviour of till. If we assume that till behaves as a viscous fluid, then using mean strain-rate data gained from tilt cells (Table 1), till viscosity, η, can be calculated from
where τ
b is basal shear stress calculated from surface survey data and borehole drilling depths using the method detailed by Reference Kamb and EchelmeyerKamb and Echelmeyer (1986) that takes into account the effects of longitudinal stress gradients, and
![]() is the down-glacier strain rate. The shear stresses calculated by this method are 37 kPa down-glacier of the surge front and 56 kPa up-glacier of the surge front. Viscosity estimates for Bakaninbreen till calculated from tilt-cell data are given in Table 1.
is the down-glacier strain rate. The shear stresses calculated by this method are 37 kPa down-glacier of the surge front and 56 kPa up-glacier of the surge front. Viscosity estimates for Bakaninbreen till calculated from tilt-cell data are given in Table 1.
In situ measurements of till viscosity have also been made at Bakaninbreen using data gained from ploughmeters installed at the bed (Table 2). The viscosities measured using ploughmeters and tilt sensors are in good agreement down-glacier of the surge front (Tables 1 and 2). Here, viscosity estimates at Bakaninbreen are up to four orders of magnitude higher than those reported from the studies elsewhere (Table 2). Given that Bakaninbreen is thought to override marine muds in the lower reaches (Reference Hambrey, Dowdeswell, Murray and PorterHambrey and others, 1996), these high values are surprising. One potential explanation is that the basal till layer at Bakaninbreen is frozen in this region. Up-glacier of the surge front the two sets of instruments are not in good agreement (Tables 1 and 2), and the ploughmeter results suggest that the till is not frozen in this region. Our analysis has assumed that all of the tilt registered by our sensors results from deformation within the till layer rather than sliding at the ice-bed interface. If, however, some motion actually results from sliding, this would increase rather than reduce the viscosities calculated from tilt-cell data. Based on our inference of the dominance of deformation over sliding discussed above, and the agreement between ploughmeter and tilt-cell data below the surge front, we suggest that the discrepancy between the two data sources above the surge front is real and needs to be accounted for. We suggest that the high viscosities calculated using the tilt sensors (Table 1) are anomalous and result from the assumption inherent in Equation (4) that it is the viscosity of the till alone that provides the resistance to glacier motion. Rather, we believe that the disparity in the two estimates suggests that, while the presence of soft sediments beneath the glacier may facilitate flow, their shear resistance does not control the rate of glacier flow in this region up-glacier of the surge front. This situation is closely analogous to that of Ice Stream B, Antarctica, where the rate of flow is thought to be controlled by either basal sticky spots or side-wall friction (e.g. Reference AlleyAlley, 1993; Reference Jackson and KambJackson and Kamb, 1997). We suggest that at Bakanin-breen similar mechanisms or the buttressing effect of the inactive ice down-glacier of the surge front must support some portion of the basal shear stress.
Table 2. In situ basal till viscosity estimates
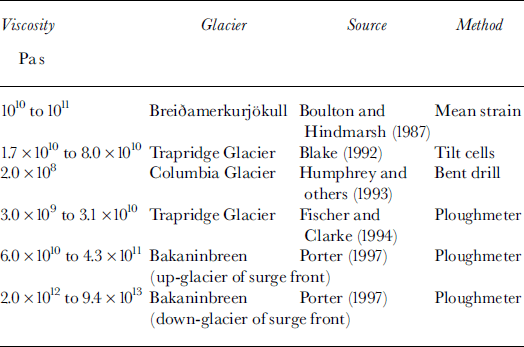
Although use of strain-rate data from tilt sensors can potentially provide a useful insight into the mechanical properties of basal till, a number of factors need to be taken into account when interpreting such data. Reference BlakeBlake (1992) suggested that the concept of viscosity may not be appropriate for describing deformation in granular materials, as particle interactions within the till layer are unlikely to consist of elastic collisions, while tilt sensors will inevitably exhibit localized interaction with clastic material. This problem is highlighted by Reference Boulton and DobbieBoulton and Dobbie (1998) with reference to strain markers inserted into the till layer beneath Breiðamerkurjökull, Iceland (Reference Boulton and JonesBoulton and Jones, 1979). Individual strain markers show different patterns of rotation that are related to localized flow patterns, rather than larger-scale patterns of strain within the till layer. Deriving a viscosity for what is regarded as a homogeneous till layer on the basis of the motion of individual tilt sensors is therefore a potential limitation of the experimental design. Reference BlakeBlake (1992) suggested that this problem could be partially overcome by averaging strain rates over time. This technique was applied in deriving the viscosity estimates for Trapridge Glacier till, presented in Table 2, with strain rates averaged over periods of 4–5 days.
The records of strain rate from Bakaninbreen range from a little over 4 months to 18 months in duration (Fig. 3). The viscosity estimates calculated from tilt cells (Table 1) are obtained by taking the mean strain rates over the entire period of observation for each individual sensor in order to overcome the problems outlined above. In addition, it is useful to calculate mean strain rate over various segments of the time series and assess the impact this has on the resultant viscosity estimates. Strain rates were averaged over 10 day segments and viscosities calculated. Figure 5 presents these data together with the original strain-rate data. Viscosity estimates presented in Figure 5 vary by up to four orders of magnitude, indicating that simple averaging of the strain-rate record does not adequately smooth localized motion of the tilt sensors. Tilt sensors provide information on localized strain events, but they may be unable to provide information on larger-scale patterns of strain within the till layer, particularly if inhomogeneous deformation or folding occurs (Reference Boulton and DobbieBoulton and Dobbie, 1998).
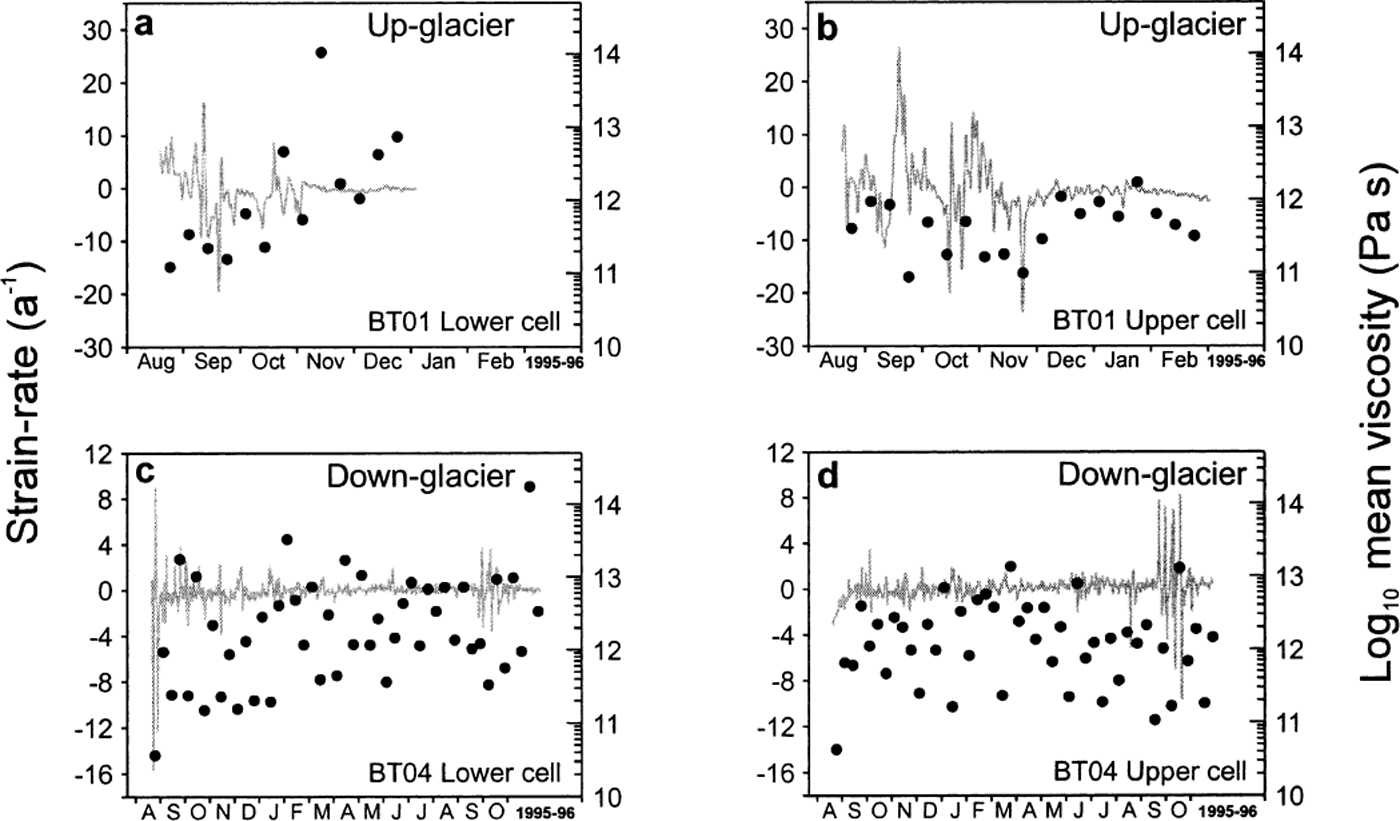
Fig. 5. Strain-rate data from tilt sensors (grey lines) with 10 day mean viscosity estimates superimposed (black dots).
Hydraulic Properties of Basal Sediments
Hydraulic properties of basal till
The diffusivity of a basal till controls how rapidly changes in pressure are propagated (Reference FountainFountain, 1994; Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others, 1995; Reference MurrayMurray, 1997). For a harmonic forcing, /, at the surface of a half-space, the till diffusivity can be calculated from the measured lag, t, between the forcing signal and the response (Reference Carslaw and JaegerCarslaw and Jaeger, 1959). The choice of which of the pressure signals is the forcing function is determined by cross-correlation, which shows that up-glacier of the surge front pore-water pressure lags borehole water pressure by 37–49 hours. This observation implies that the water pressure at depth in the till is driven by changes in water pressure in the borehole. The diffusivity, D, is given by

where x is the insertion depth of the pore-water transducer within the till (after Reference Carslaw and JaegerCarslaw and Jaeger, 1959). The value of f is taken to be the dominant frequency of the borehole pressure signal obtained by Fourier analysis. This frequency was 0.02–0.5 d−1. The resulting diffusivity value ranges between 1.2 × 10−6 and 5.0 × 10−6 m2 s−1, values that are in agreement with those from other sites (Table 3).
Table 3. Hydraulic properties of basal sediments

It is also possible to estimate the hydraulic conductivity from
where S s is the specific storage of till (Reference Freeze and CherryFreeze and Cherry, 1979), here taken to be 0.064 m1 (Reference Murray and ClarkeMurray and Clarke, 1995). The hydraulic conductivity of the basal till at Bakaninbreen ranges from 3.2 × 10−7 to 7.7 × 10−8 m2 s−1 and, like our diffusivity calculations, is in good agreement with conductivity calculations made elsewhere (Table 3).
Although it appears that our tilt sensors are recording localized strain events, the question arises as to whether or not pressure changes observed in the region of our tilt sensors are being driven by larger-scale water-pressure changes elsewhere. Following the analysis of Reference Barrett and CollinsBarrett and Collins (1997), we assume that water-level fluctuations recorded in boreholes are driven by pressure changes in the basal hydrological system. It is possible to calculate from the diffusivity the distance d over which pressure fluctuations generated at one location of the bed and propagated through the till layer will still be resolvable by our pressure transducers. This distance, d, is given by

where A 0 is borehole water-pressure amplitude, and A is the minimum measurable water-pressure fluctuation. Our pressure transducers have a resolution of 0.025 m. The amplitude of the pressure signal registered by the borehole pressure transducer located up-glacier of the surge front is 27 m; applying our calculated ranges of w and D yields a horizontal distance of 14–46 m over which any pressure pulse may propagate through the basal till layer and still be measurable by our pressure transducers. The amplitude of the pressure pulse against distance from borehole can then be calculated from
Results of this calculation for our range of w and K values are shown in Figure 6. Pressure amplitude declines rapidly with distance from the borehole, with all scenarios yielding negligible pressure amplitudes within 10–30 m of the borehole (Fig. 6). Thus, it seems likely that observed pressure changes are essentially localized phenomena. This analysis assumes laminar water flow through sediments that are both homogeneous and isotropic.
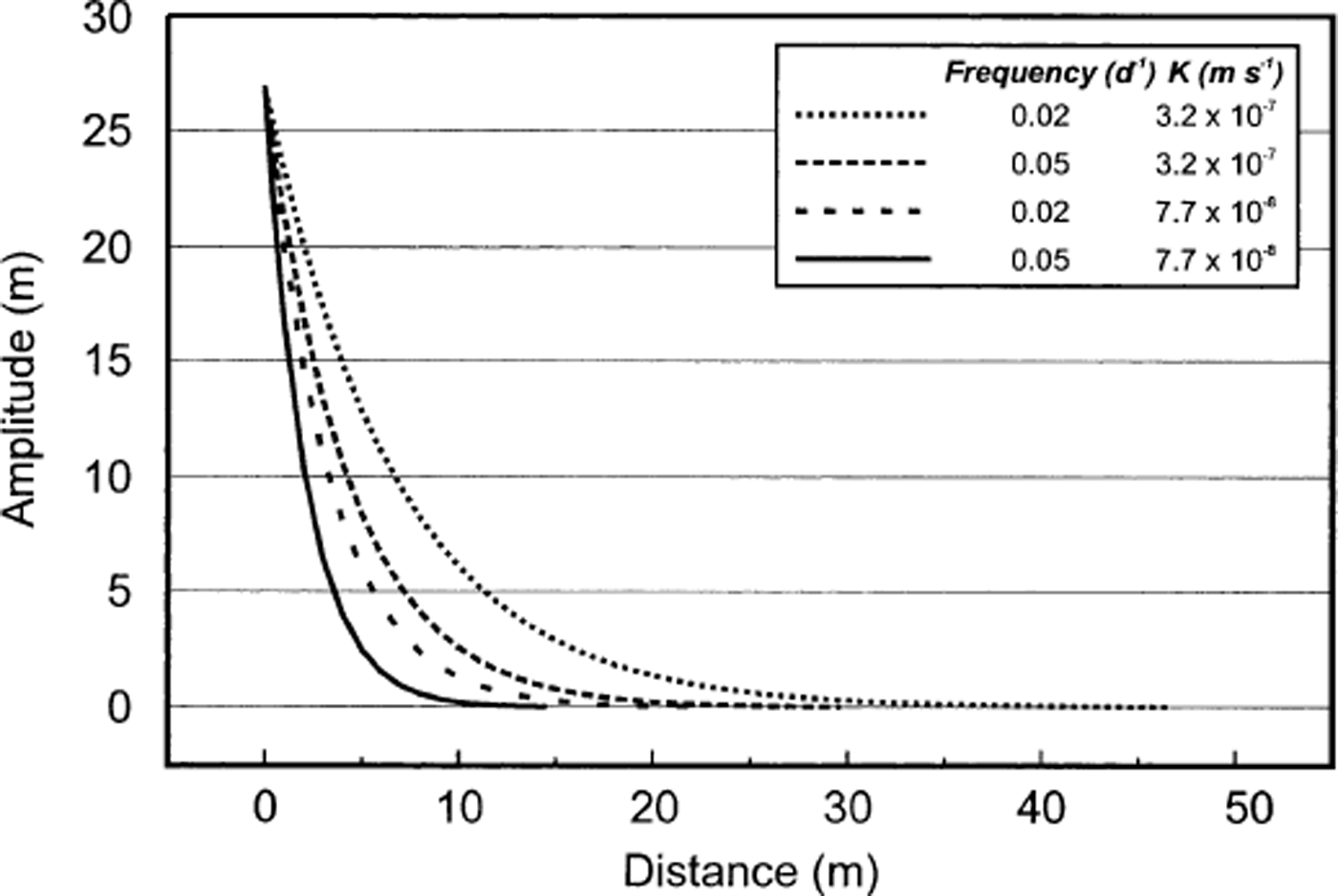
Fig. 6. Water-pressure amplitude with distance from borehole up-glacier of the surge front, as calculated from Equation (8).
Effective-pressure-strain-rate relationships
Effective pressure is a fundamental component of attempts to formulate a constitutive relation between shear stress and strain rate in basal till. However, the exact nature of the relationship between effective pressure and strain rate remains unclear. Experiments performed at the margins of Breiðamerkurjökull provided a rheological relationship for glacial till (Boulton andjones, 1979; Reference Boulton and HindmarshBoulton and Hindmarsh, 1987). Data collected consisted of measures of average strain rate and water pressure in the upper basal till layer, and calculated values of average shear stress and overburden pressure. The data were fitted to two rheological models relating strain rate to shear stress and effective pressure, assuming that till behaves as either a non-linear viscous fluid or a Bingham fluid. Criticisms of the Breiðamerkurjökull experiments are well documented, largely centred upon the marginal location of the study site, where basal mechanical and hydrological conditions may be dissimilar to those existing away from the ice margins, and the method of calculating basal shear stress (Reference Hooke, Hanson, Iverson, Jansson and FischerHooke and others, 1997).
The two rheological relationships derived from the Breiðamerkurjökull experiments indicate a direct relationship between stress and strain rate, and an inverse relationship between strain rate and effective pressure. The question arises as to the applicability of the Breiðamerkurjökull flow relations to other glaciers. At Bakaninbreen, we have the advantage of being able to determine effective pressure from pressure fluctuations measured within the basal till layer instead of relying on borehole pressure measurements as a surrogate. Cross-correlation of strain rates within the till layer and effective-pressure records yields no clear or consistent relationship. Furthermore, application of the Breiðamerkurjökull flow relations to effective-pressure data from Bakaninbreen results in underestimation of observed mean strain rates within the basal till layer.
Other studies have also failed to corroborate the Breiðamerkurjökull flow relationship. Field data from Storglaciaren, Sweden, failed to demonstrate the inverse relationship between effective pressure and strain rate (Reference Hooke, Hanson, Iverson, Jansson and FischerHooke and others, 1997). Instead, high strain rates within the basal till layer were associated with high effective pressures, suggesting that decreasing water pressure increases the coupling between the glacier and its bed, resulting in higher strain rates. Conversely, increasing water pressure decreased coupling, with a resultant decrease in strain rate within the basal till layer, and an increase in sliding at the ice–bed interface. Furthermore, applying the Breiðamerkurjökull flow relations to a 4 day segment of average strain-rate and effective-pressure data collected from Trapridge Glacier, Reference BlakeBlake (1992) found that the viscous model greatly underestimated observed strain rates. No deformation was predicted for the Bingham-fluid model, as the calculated yield strength of the basal till was never exceeded. These findings led Reference BlakeBlake (1992) to the conclusion that the Breiðamerkurjökull flow relations were not applicable to Trapridge Glacier till. The effective pressure data from Trapridge Glacier used in Blake’s calculations were derived from borehole pressure sensors. It is thought that the bed of Trapridge Glacier comprises a layer of hydraulically conductive till near the ice–bed interface underlain by a layer with lower conductivity, and therefore that at this glacier a borehole pressure is likely to be a reliable surrogate for pressure fluctuations in the upper till layer (Reference BlakeBlake, 1992).
The general failure of the Breiðamerkurjökull flow relations to predict observed strain rates highlights the problems of deriving a stress-dependent rheology for basal till. Relationships between the basal water system and strain rates within the till layer are likely to display complex feedbacks, and derivation of a flow relation for basal till on the basis of a simple relationship between these two systems is problematic. This conclusion is supported by the lack of a clear, consistent relationship between effective pressure and strain rates within the basal till layer at Bakaninbreen.
Throughout the discussion in this paper we have assumed that the till beneath Bakaninbreen can be modelled as a viscous fluid. Recent laboratory experiments suggest that till may better be represented as a Coulomb plastic (Reference Iverson, Hooyer and BakerIverson and others, 1998; Reference Tulaczyk, Mickelson and AttigTulaczyk, 1999; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000). Many features of our results can be explained by this model, such as the presence of distributed shear and the occurrence of both negative and positive strain rates (Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000). However, fundamental to the plastic model is the relationship between failure and effective pressure, so that strain rate and effective pressure should be strongly correlated (Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000, fig. 7). Our data do not show this correlation.
We must take into account limitations of the experiment design discussed earlier that might mask the existence of a relationship between effective pressure and strain rate that is a feature of both viscous and plastic models. However, if the apparent complexity of the basal water and sediment systems beneath Bakaninbreen is real, this suggests that neither of the present viscous or plastic models may be adequate. This has implications for the use of High Arctic glaciers as analogues for those seeking to model the behaviour of former ice masses. Further research into the basal mechanical and hydrological regimes of High Arctic glaciers is required in order to resolve the complexities that this study presents.
Concluding Remarks
Data gained from tilt sensors installed within the basal till layer at Bakaninbreen indicate higher (by an order of magnitude) strain rates up-glacier of the surge front than down-glacier of it. The time series from all tilt sensors exhibited fluctuations, including both positive (down-glacier) and negative (up-glacier) strain rates. Using the measured strain rate, an estimate of till viscosity is obtained that is of a magnitude that might indicate that the till layer is frozen in places; values range from 1.3 × 1012 to 3.4 × 1012 Pa s. Limitations of the experiment design suggest that careful interpretation of results from tilt sensors is required. However, interpretation of angular fluctuations registered by tilt sensors indicates that sediment deformation at Bakaninbreen dominates basal motion. Results from pore-pressure sensors installed within tilt sensors, along with standard borehole pressure transducers, allow hydraulic properties of the till layer to be estimated. The hydraulic diffusivity of the Bakaninbreen till ranges from 1.2 to 5.0 × 10−6 m2 s−1, and hydraulic conductivity ranges from 3.2 × 10−7 to 7.7 × 10−8 2 s−1. Both strain-rate and water-pressure fluctuations appear to be localized phenomena. At Bakaninbreen, no clear, consistent relationship between these two variables was apparent, suggesting that neither the Breiðamerkurjökull flow relations (Reference Boulton and JonesBoulton and Jones, 1979; Reference Boulton and HindmarshBoulton and Hindmarsh, 1987) nor plastic-Coulomb models are appropriate to describe till mechanics at this glacier.
Acknowledgements
This research was funded by grants from the U.K. Natural Environment Research Council (GT3/9031) and the European Union (EN5V-CT93-0299). A University of Leeds, School of Geography Studentship provided personal support to P.R.P. The School of Geography also provided funding for our hot-water ice-drilling system. We are grateful to E. Blake for supplying advice on electrolytic tilt cells, and to F. Olsen and J. Pedersen (Norwegian Polar Institute) and R. Ødegård and J.-O. Hagen for invaluable help with our 1995 summer and 1996 spring field seasons. Thanks are due to the Sysselmann of Svalbard for allowing us to conduct long-term monitoring at Bakaninbreen, and to D. Gooch and A. Hiatt for field assistance in 1995. Insightful comments by W. D. Harrison, B. P. Hubbard, B. Kulessa and an anonymous reviewer improved this paper.











