Article contents
Wake of wavy elliptic cylinder at a low Reynolds number: wavelength effect
Published online by Cambridge University Press: 15 August 2023
Abstract
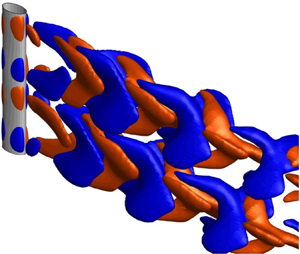
Effects of the spanwise wavelength (λ) of a sinusoidal wavy cylinder with elliptic cross-section on wake structures and fluid forces are numerically investigated at a Reynolds number Re = 100. A wide range of the wavelength,  $0.43 \le \lambda /{D_m} \le 8.59$, is considered with a wave amplitude of a/Dm = 0.048, where Dm is the hydraulic diameter of the wavy cylinder. Based on vortical structures, Strouhal number (St) and wake closure length (Lc), fluid forces, streamline topologies and spatio-temporal evolutions of the near wake, five distinct flow patterns (I–V) are identified depending on λ/Dm. The drag force reaches its minimum in pattern III, the fluctuating lift force is zero in flow patterns III and IV. Distinct from the classical flow where alternate vortex shedding occurs synchronously over the entire cylinder span, flow pattern IV has alternate vortex shedding over a one half-wavelength of the wavy elliptic cylinder, antiphased with that over the other half-wavelength, thus leading to zero fluctuating lift over one complete wavelength. A thorough comparison of the wakes is made between the wavy elliptic cylinder and wavy circular or square cylinder, distinguishing the underlying flow physics behind the salient behaviours observed.
$0.43 \le \lambda /{D_m} \le 8.59$, is considered with a wave amplitude of a/Dm = 0.048, where Dm is the hydraulic diameter of the wavy cylinder. Based on vortical structures, Strouhal number (St) and wake closure length (Lc), fluid forces, streamline topologies and spatio-temporal evolutions of the near wake, five distinct flow patterns (I–V) are identified depending on λ/Dm. The drag force reaches its minimum in pattern III, the fluctuating lift force is zero in flow patterns III and IV. Distinct from the classical flow where alternate vortex shedding occurs synchronously over the entire cylinder span, flow pattern IV has alternate vortex shedding over a one half-wavelength of the wavy elliptic cylinder, antiphased with that over the other half-wavelength, thus leading to zero fluctuating lift over one complete wavelength. A thorough comparison of the wakes is made between the wavy elliptic cylinder and wavy circular or square cylinder, distinguishing the underlying flow physics behind the salient behaviours observed.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 8
- Cited by



